【中学受験算数】問題文にだまされないで！行きと帰りの速さから平均の時速を求めるにはどんな面積図を書けばいい？

はじめに

みなさんこんばんは！
今日も「速さ」に関する問題に挑戦ちょうせんしていきましょう。
この問題をヒントなしで解きたい！という受験生はさっそく問題から解いてみてください。
解くまえに少しヒントが見たい受験生はこちらから読むとよりわかりやすくなると思います。

速さの基礎きそを復習しよう！

まずは「速さ」について復習しておきましょう。

速さとは？

速さとは、どれくらいの距離をどれくらいの時間で進んだのかを表すものです。

例たとえば、
体重はその人の重さを表しているもの、
視力しりょくはその人の目の良さを表しているものになりますね。

速さもそのような何かを表しているものの仲間なかまの一つです。

平均について理解しておこう！

小人たちのテストの平均点は？

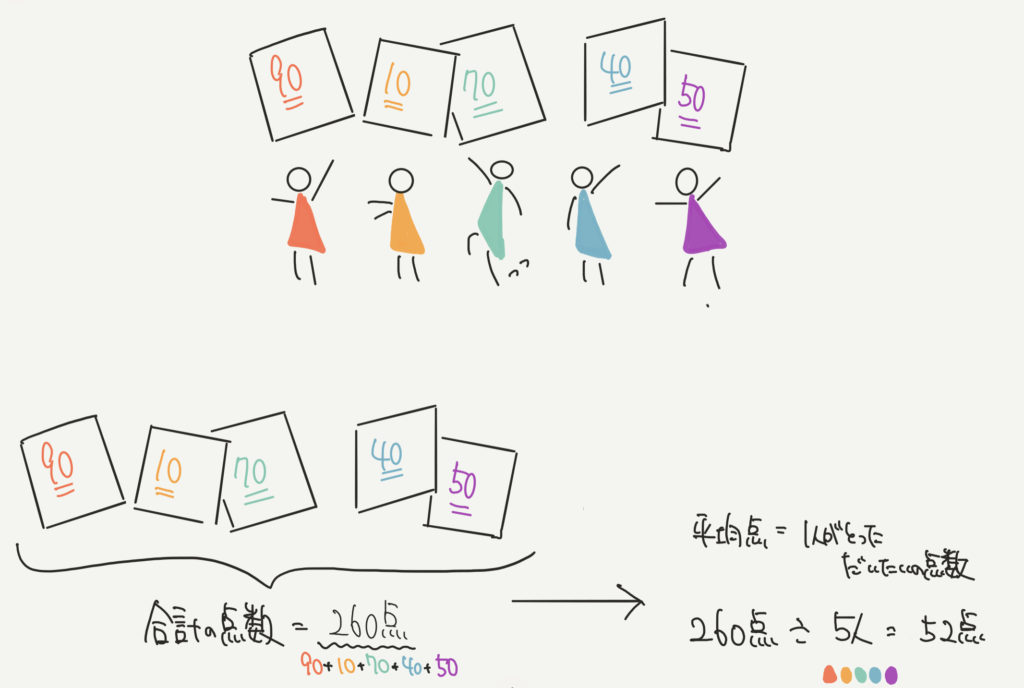
例えば、赤、黄、緑、青、紫の5人の小人がいたとします。
彼ら5人のテストの平均点（1人あたりだいたいどれくらいの点数を取ったのか）を求めるには、
全員のテストの合計点÷小人の人数＝平均点、と求もとめることができましたね。

よって今回は、
(90+10+70+40+50)÷5人＝52点/人（1人あたり52点）とっていることがわかります。

男女の平均の長さから女子の平均を求めるには？

復習ですが、平均とは、超かんたんに言うと「だいたいこれくらい！」という数のことでしたね。
平均の考え方について、まだ意味がよく分からない、もう少しきちんと理解したい、という受験生はこちら↑の記事でとても詳くわしく説明しています。
もし時間と合格する気があればぜひ勉強してから、今日の問題にチャレンジしてみましょう！

問題に挑戦ちょうせん！

6kmの坂道を、行きは毎時6km、帰りは毎時12kmの速さで往復おうふくしました。
このとき、往復の平均の速さは毎時何kmですか。

解答

この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略こうりゃくしよう！

STEP1：要注意ようちゅうい！！速さの平均と平均の速さは全く違ちがう！！

平均の速さと聞いて9km/時と書いてしまった人も多いのではないでしょうか。
それでは単純たんじゅんに行きと帰りの速さの平均です。

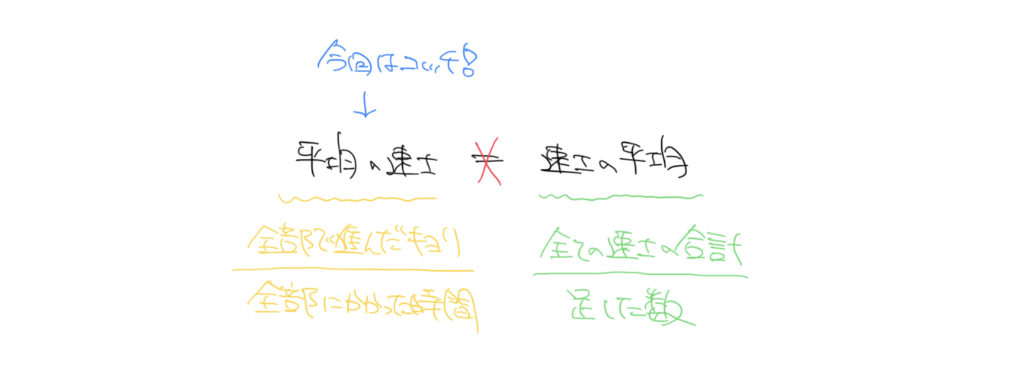
問題で聞かれているのは速さの平均ではなくて、往復おうふくの平均の速さです。
まずは何をきちんと答えるべきなのかを確認しておきましょう。
答えるものを間違まちがえてしまえばせっかく計算しても意味がなくなってしまいますので気をつけましょう。

STEP2：速さの平均を求もとめると間違まちがえてしまう！

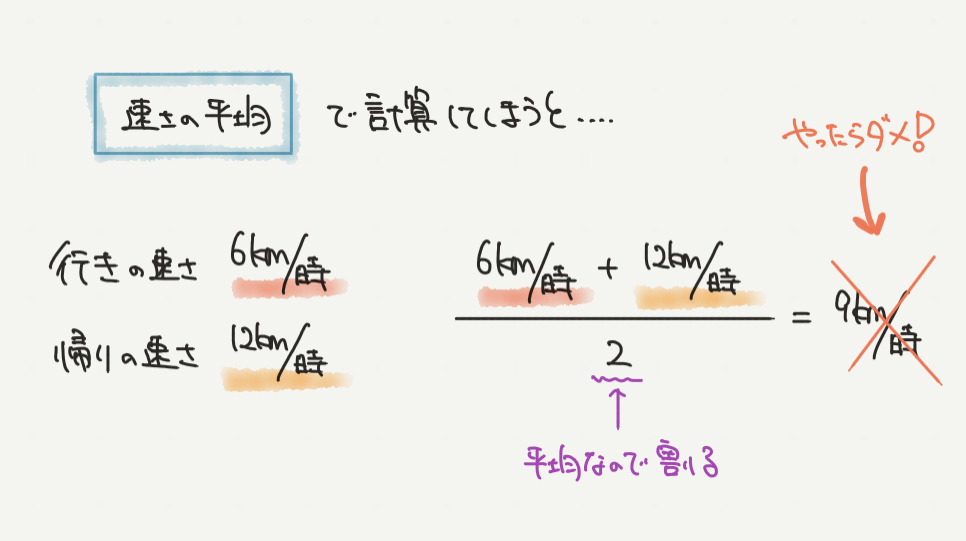
速さの平均を求めてしまうと、（6km/h+12km/h）×1/2=9km/hと計算してしまいます。
このやり方で計算してはダメなので気をつけましょう！

それではSTEP3で速さの平均を求めていきましょう。

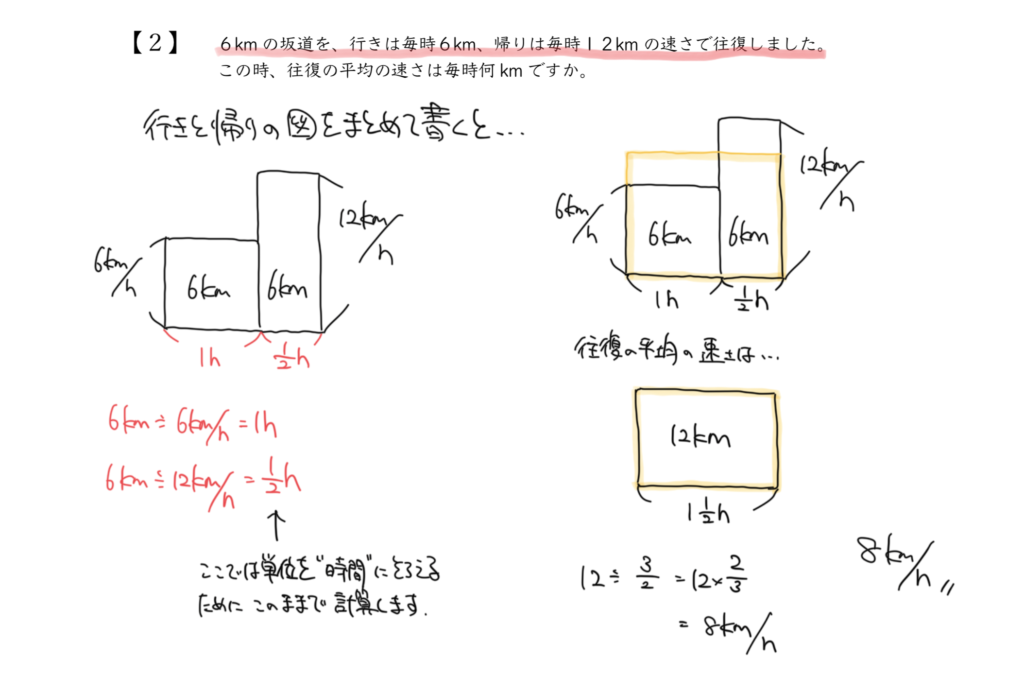
STEP3：平均の速さを求もとめよう！

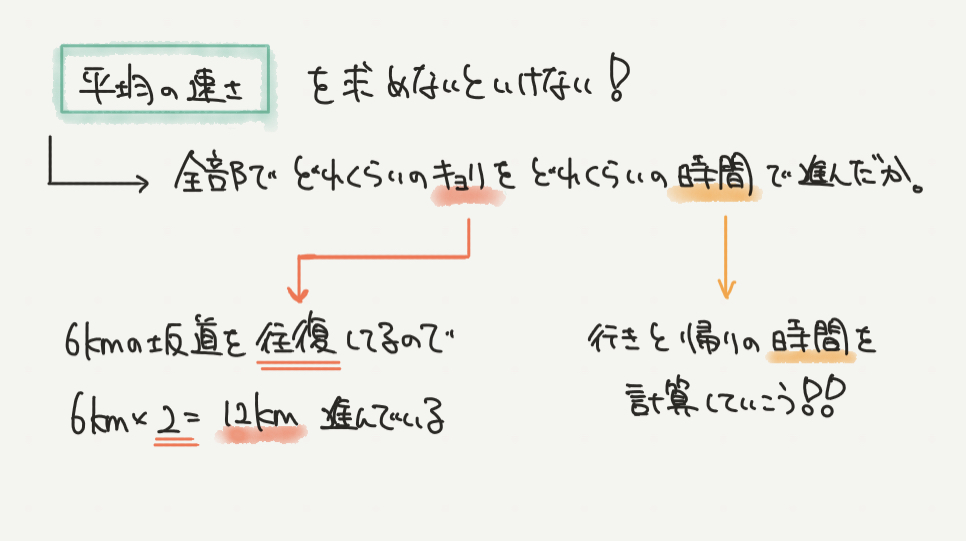
求もとめる必要のある平均の速さは、
全部でどれくらいの距離きょりをどれくらいの時間で進んだのかが分かれば計算できます。

片道6kmの坂道を往復おうふくするで全部で進む距離きょりは12kmになります。

そして進むのにかかる時間ですが、行きは1時間、帰りは30分（1/2時間）で帰ったので、
行き：6km÷6km/時＝1時間
帰り：6km÷12km/時＝1/2時間
で、全部で3/2時間かけて走ったことになります。

よって12km÷3/2時間で答えを8km/時と求めることができました。

行きと帰りの速さから平均の時速を求める問題のまとめ

今回の問題で大事なポイント

平均の考え方
・面積図で平均を表してみよう
・同じところを見つけよう
速さの平均と平均の速さは全く違ちがうので注意！！

以上で速さの問題は終わりです。
今日もよくがんばりましたね！おつかれさまでした！！

今回の問題で重要だったのは、
①平均の考え方
②速さの平均と平均の速さは違ちがう
という2つでした。

①と②はほとんど同じですが、これを勘違かんちがいしてしまうと計算が全部あっていてもバツになってしまいます。

ですので今後も問題を解くときはかんたんだからと言って油断ゆだんせずに、まずは何を聞かれているのか？何を答えないといけないのか？を確認するようにしましょう。

その他の単元の問題の復習はこちらから！