【中学受験算数】仕事算の問題は仮定の考えと面積図が超重要！AとBが仕事を終えるまでの日数を面積図を書いて求めてみよう！

はじめに

みなさんこんばんは！
まだ成績が上がらない受験生もまだ間に合います。今からでもきちんと勉強して合格を勝ち取りましょう！

さて、今日解く問題は「仕事算」に関する問題です。

それでは「仕事算」の復習からです！

仕事算の復習！仕事量を仮定しよう！

基本的には1人が1時間かけてやる仕事を①と仮定する

仕事算では「仮定する」考え方が大事です。
この仮定する考えというのは、「もし○○が□□だったら～」と問題を解きやすくするための考え方のことです。

今回は「もし1人が1時間で働く仕事の量が①だったら～」と仮定しています！
ただ、問題によっては1人が仕事する量を仮定するのではなく、全体の仕事量を○で仮定する場合があります。

そういう問題も練習していきましょう！
それでは問題に挑戦です！！

問題に挑戦ちょうせん！

ある仕事をするのに、Aだけでは14日、Bだけでは35日だけかかります。
この仕事をA、B2人でいっしょにすると、何日かかりますか。

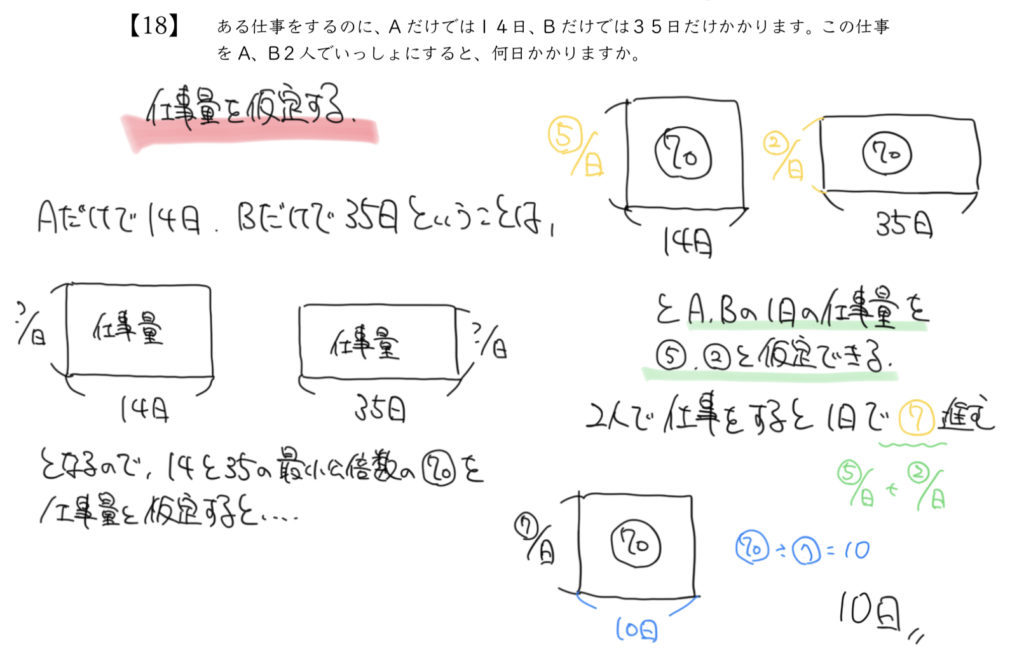
解答

この記事を書いている人はこんな人

解説を読んで「 割合と比 」を攻略こうりゃくしよう！

STEP1：問題文を図にしてみよう

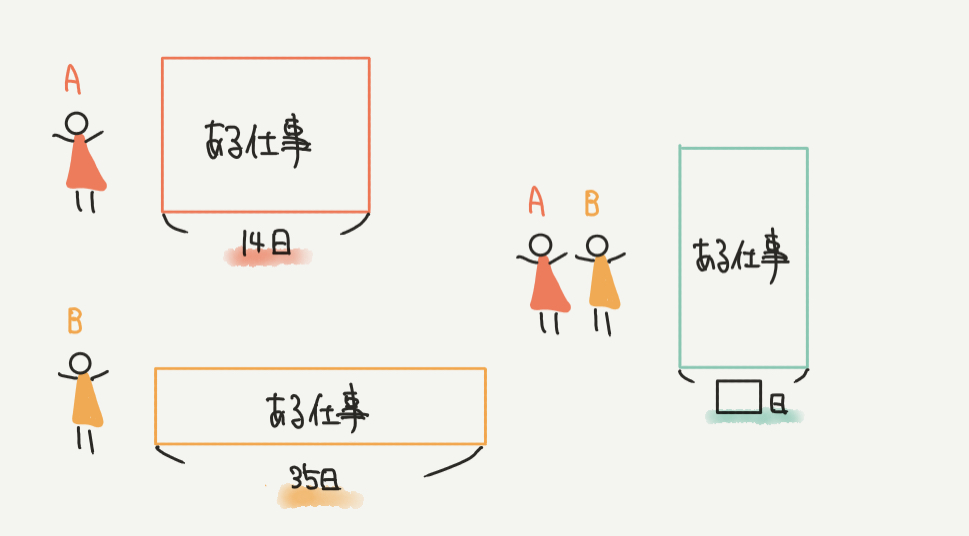
まずはいつも通り、問題文を図にしてみましょう。
Aは14日で仕事を終えるので、横が14日になりますね。
それに比くらべてBでは同じ仕事をするのに35日の時間がかかっているので、Bの面積図の横が35日となります。

今回求もとめたいのは、AとBが2人で同じ仕事をしたときにかかる日数なので、
まずはSTEP1で何を答えないといけないのかを確認しましょう。

STEP2：なにを仮定するのか考えよう

さて、ここからが「仕事算」の大事なポイントです。
今までの問題の解説では1人が行う仕事の量を①と仮定していました。

なぜならそのやり方で計算するやり方が一番わかりやすく、解きやすかったからです。
ただ、今回①と仮定して計算してしまうと正解はできますが時間がかかってしまいます。
↑多分解いている途中とちゅうで、気づくと思います。あれ？めんどくさくね？って

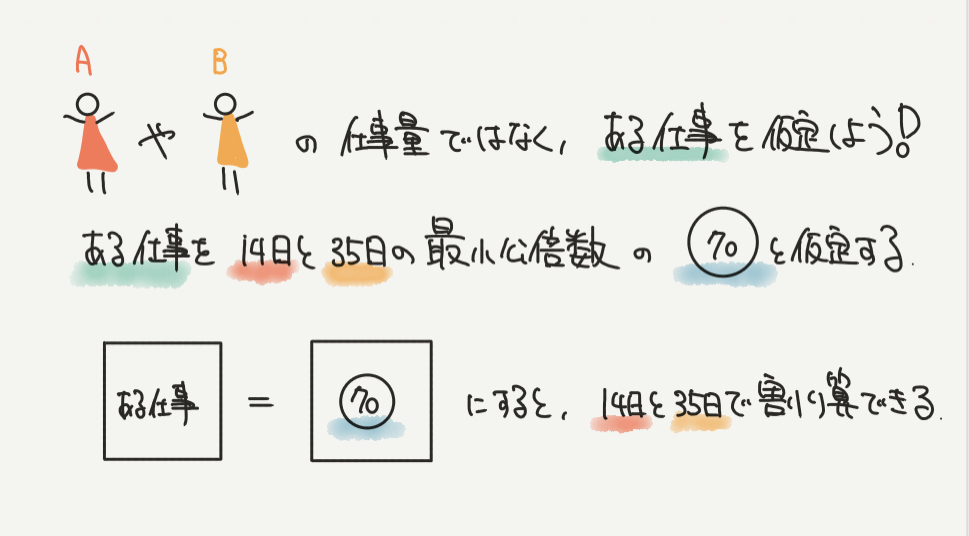
そこで今回はある仕事の量を仮定していきましょう。
14日と35日で割り切れる数字で仮定すると問題が解きやすくなるので、
14と35の最小公倍数である◯の70と仕事量を仮定して解いていきます。

STEP3：ある仕事量からAとBの仕事量を求もとめよう

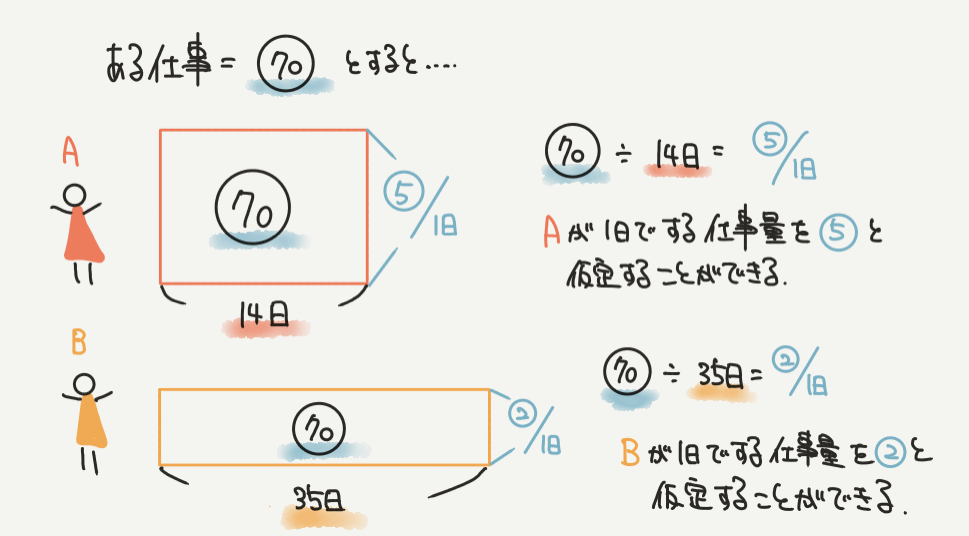
STEP2で、ある仕事量を○の70と仮定したので、

ここから
Aの1日の仕事量＝○70÷14日＝⑤/1日
Bの1日の仕事量＝○70÷35日＝②/1日
と求もとめることができますね！

ポイント：算数ができる受験生の目のつけどころ

ちなみに、面積が同じ（仕事量が同じ）で横の長さの比が14日:35日＝2:5なので
たての比は逆比になり5:2になっていることが確認できます。
逆比の問題はこちらを復習してみてください。

クラスの平均点からクラスの人数の比を求めるには？

STEP4：最後は答えを出していくだけ！

最後は解くだけです。
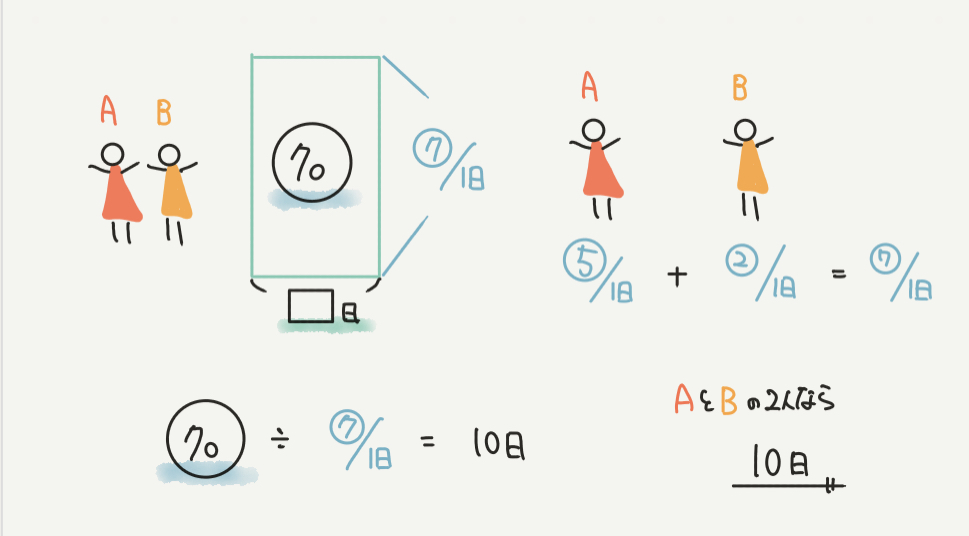
STEP2である仕事量を◯の70と仮定して、

AとBの仕事量の合計（1日で進められる仕事量）が⑤+②＝⑦とわかるので、
かかる日数は○70÷⑦/1日＝10日になります。

それぞれの仕事量から、仕事を終えるまでの日数を求める問題のまとめ

今回の問題で大事なポイント

仕事算の考え方（何を仮定するのか？）
・仕事量を仮定していきましょう！（今回は1人が1時間やる仕事を①と仮定しました）
面積図の書き方（書き方はきちんと理解していますか？）

この問題で大事だったポイントは、
①仕事算の考え方（何を仮定するのか？）
②面積図の書き方（書き方はきちんと理解しているか？）
の2点でした。

そしてさらに合格に近づくポイントとして、
③逆比についての考え方（四角形の面積が同じならたての比と横の比は逆になる！）
がありましたね。

どのポイントも復習できる記事がありますので、ぜひふりかえりながら時間をかけてゆっくりと勉強してみください。
テストでは早く解くことが大事ですが、復習や自習ではゆっくりていねいに解くことが大事ですよ！

その他の単元の問題の復習はこちらから！