【中学受験算数】苦手の生徒の多い割合と比を攻略！！まずは表を見て比例と反比例を勉強しよう！

はじめに

今日からは「割合と比」というテーマで一緒いっしょにがんばって勉強していきましょう！
「割合と比」というテーマは算数、数学という単元でこれからも超たくさん出てきますし、
ほとんど全ての問題でこの考えを使います。

↑数学すうがくとは？小学生受験生のみなさんが中学生になったら習う算数の応用単元おうようたんげんです。

それくらい大事な単元です。（実は1単元前の「和差算」にも割合の考え方は出てきています。）

この基礎編では、「割合と比」を1からていねいに解説していますので、
これから勉強を始める！という受験生もぜひ最後まで読んで勉強してもらえればと思います！
今回は「割合と比」の最初の一歩である比例ひれい、反比例はんぴれいから始めますので、例題れいだいはありません。

さっそく問題に挑戦ちょうせんしていきましょう！

問題に挑戦ちょうせん！

次の表は、どちらも２つの数xとyの関係を表しています。ア〜エに当てはまる数を求もとめなさい。

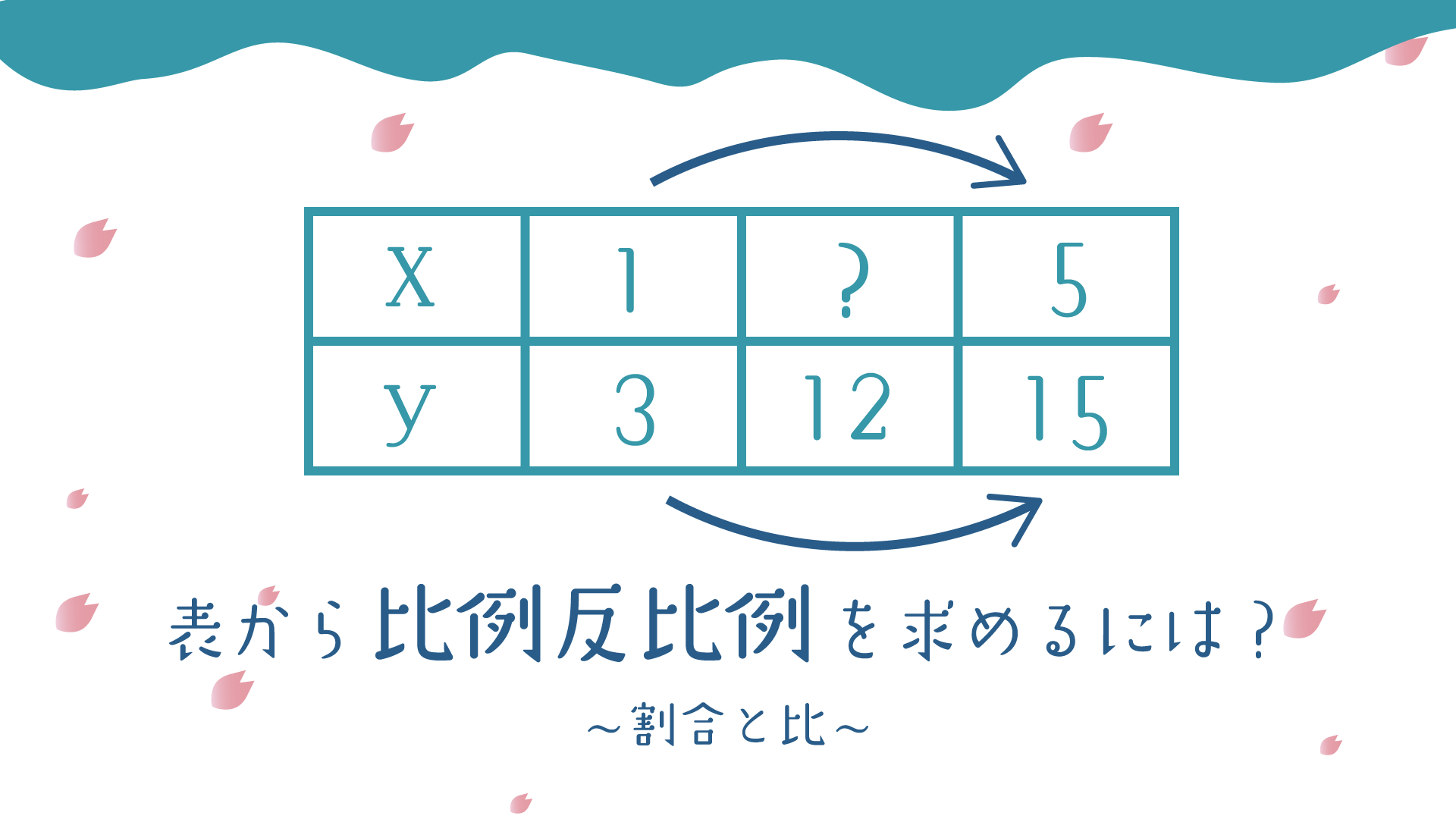
x	１	ア	５	８
y	３	12	15	イ

x	20	10	エ	１
y	４	ウ	16	80

解答

この記事を書いている人はこんな人

解説を読んで「 割合と比 」を攻略こうりゃくしよう！

STEP1：比例ひれいと反比例はんぴれいの基礎きそを理解しよう

「割合と比」でまず大切になってくるのが、比例ひれい、反比例はんぴれいの考え方についてです。
まずは比例ひれいから考えていきましょう！

比例ひれいとは？

比例とは、ある２つの数の間に見られる一定の関係のことです。

反比例はんぴれいとは？

反比例とは、2つの数の一方が2倍、3倍、…になれば、もう片方かたほうが2分の1、3分の1、…になるような、２つの数の関係、となっています。
そしてこの２つの数をかけると答えが必ず同じになるという特徴とくちょうがあります。

これだけ聞いてもいまいちわかりづらいですよね？
それではSTEP2でもっとくわしく見てみましょう！

STEP2：比例ひれい、反比例はんぴれいの具体的な例

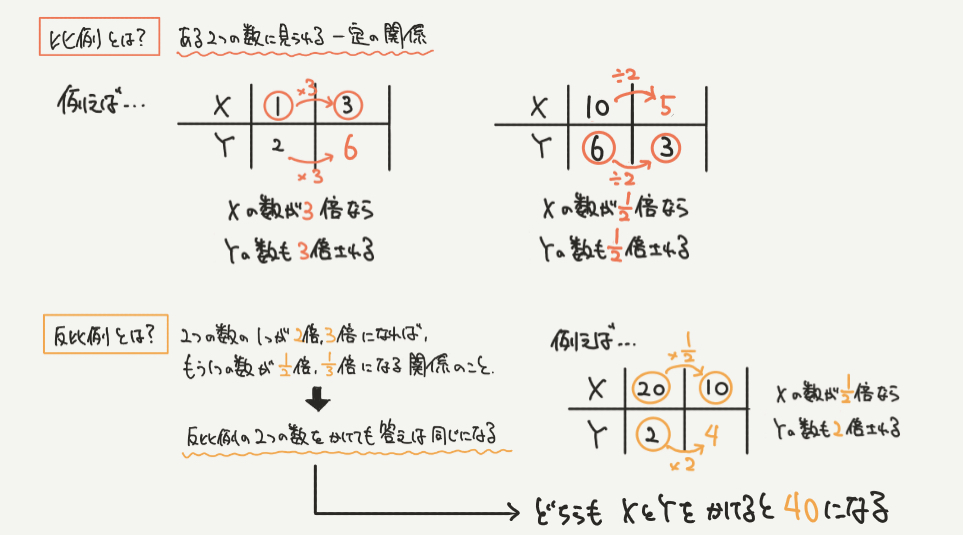
こちらの表は問題とは関係ないですが、比例ひれい、反比例はんぴれいを理解する上でおさえておきたいポイントになります。
まずはこちらのカンタンな表から比例ひれいと反比例はんぴれいを勉強しましょう。

たとえば、左上の表だと、Xが1から3に３倍されているのがわかると思います。
そして比例ひれいの表では、その3倍に合わせてYの数字も2から3倍されて6になります。

また、右上の表ではXが10から5へ1/2倍（÷2）されているので、
Yの数字も6×1/2倍（÷2）=3　となります。

右下の表を見ていただくと、
Xが20から10に1/2倍（÷2）されているのに、
Yは2から4へ2倍されていますね。

片方かたほうの数字が○倍されると、もう片方かたほうの数字は1/○倍されるのが反比例はんぴれいの特徴とくちょうになります。
今回は片方が2倍されたので、もう片方が1/2倍されていますね！

そしてこの２つの数字X＝20、Y＝2と、X＝40、Y＝1をかけるとどちらも40になりますね！
これが反比例はんぴれいの数の特徴とくちょうでもあります。

ここまで理解できればあとは問題を解くのみです！

STEP3：表をよく見て、比例ひれいか反比例はんぴれいか判断はんだんしよう！

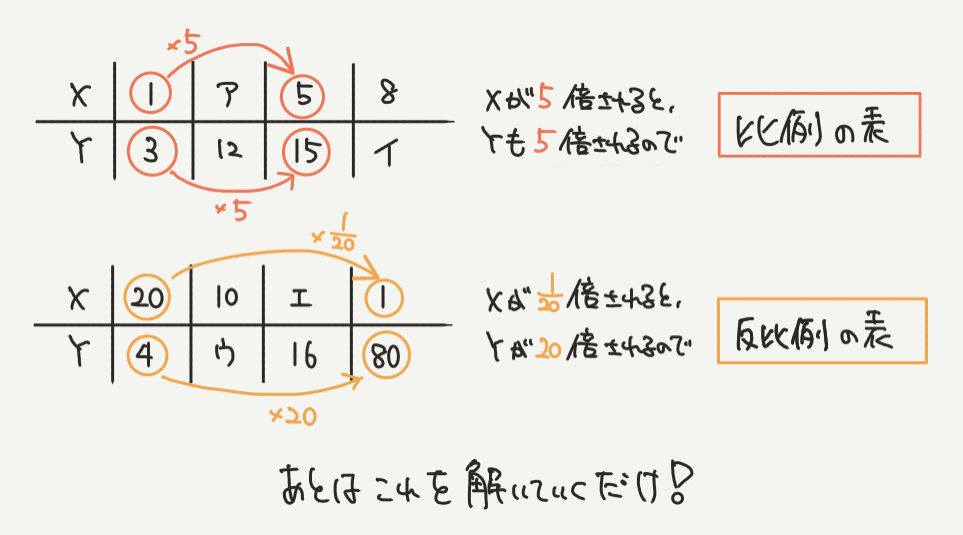
例えば上の表で考えると、
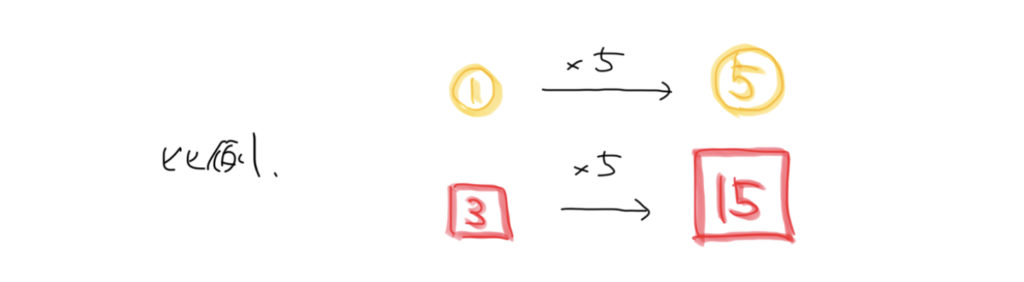
Xが1から5に5倍され、Yも3から15に5倍されていますね！
なのでこの2つの関係は、比例ひれいの関係であると言えます。

反対に、下の表を見てみましょう。
Xが20から1に1/20倍され、逆ぎゃくにYは4から80に20倍されていますね！

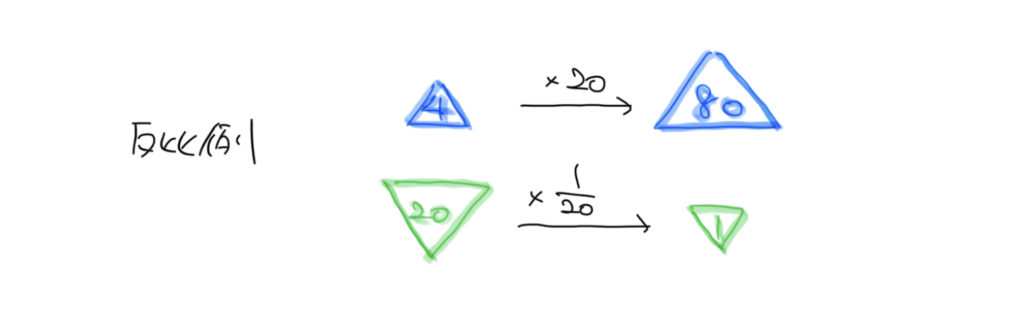
なのでここから下の表が反比例の表であることがわかります！
さあ、あと残のこり少しです！

STEP4：比例ひれい、反比例はんぴれいのルールにそって問題を解くだけ！

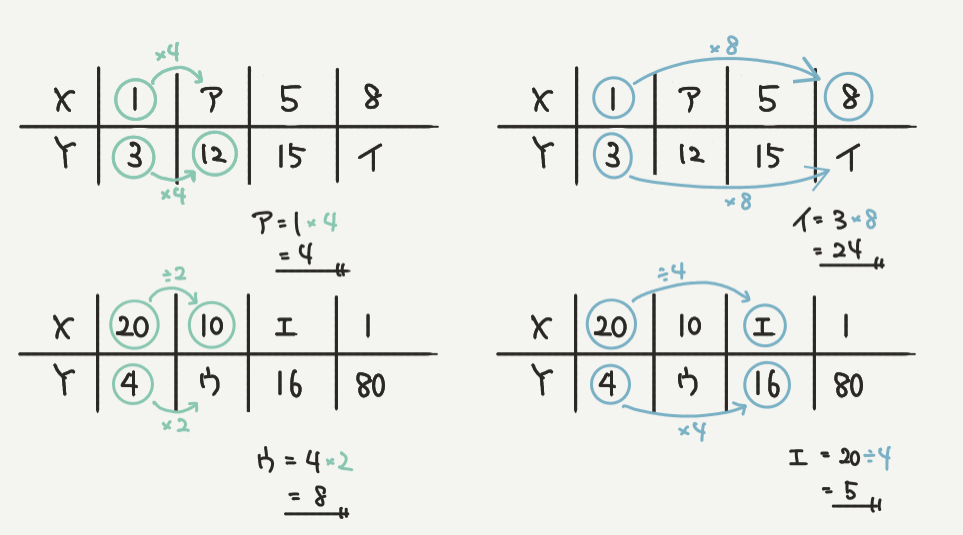
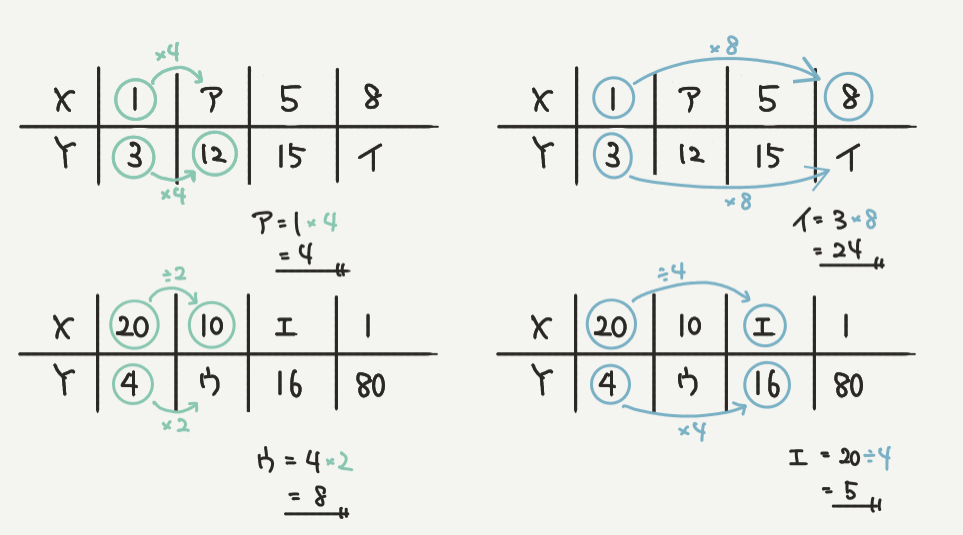
最後はSTEP 1,2,3のこれらの情報をもとに計算するだけです！

アを求もとめよう！

Xが1からアまで増ふえていますね。
下のYの方を見ると、3から12と4倍されているのがわかります。

なのでXも4倍されるので、
ア＝1×4で4となります！

イを求もとめよう！

Xが1から8まで8倍に増ふえていますね。
Yの方を見ると、3からイとなっています。

これも比例ひれいの関係なのでYも8倍されるはずです。
よって、イ＝3×8で24となります！

ウを求もとめよう！

Xが20から10まで半分（1/2倍）に減へっていますね。
こちらの表は反比例はんぴれいなので、Yは反対に2倍されることになります。

なので、
ウ＝4×2で8となります！

エを求もとめよう！

Xが20からエまで何倍かに減へっていますね。
こちらの表は同じく反比例はんぴれいなので、Xに注目すればYを求もとめることができます。

Yは4から16へ4倍されているので、Xは1/4倍されるはず。

よって
エ＝20×1/4で5となります！

表から比例と反比例を求める問題のまとめ

今回の問題で大事なポイント

比例の考え方（ある2つの数にみられる一定の関係）
反比例の考え方（2つの数の一方が2倍、3倍になれば、もう片方かたほうが2分の1、3分の1になるような2つの数の関係）

こちらの問題、いかがでしたか？カンタンでしたか？
分からないよ！ってくらいむずかしかったですか？

ていねいに解説を書きましたが、それでも分からなかったらごめんなさい！
もっとわかりやすく作れるようにがんばります！

はじめに、でも書きましたが「割合と比」はこれからもたくさん出てくる算数の問題の1つです。
ほかの問題も大事ですが、より気を引きしめてこの問題を復習するようにしましょう！

その他の単元の問題の復習はこちらから！