【中学受験算数】線分図と面積図を書いて旅人算を攻略！2人が向かい合って進むときのすれ違う時間を計算！

はじめに

みなさんこんばんは！
今日は速さの中でもとくに「旅人算たびびとざん」と呼ばれる問題にチャレンジしてきましょう。

旅人算たびびとざんってなに？

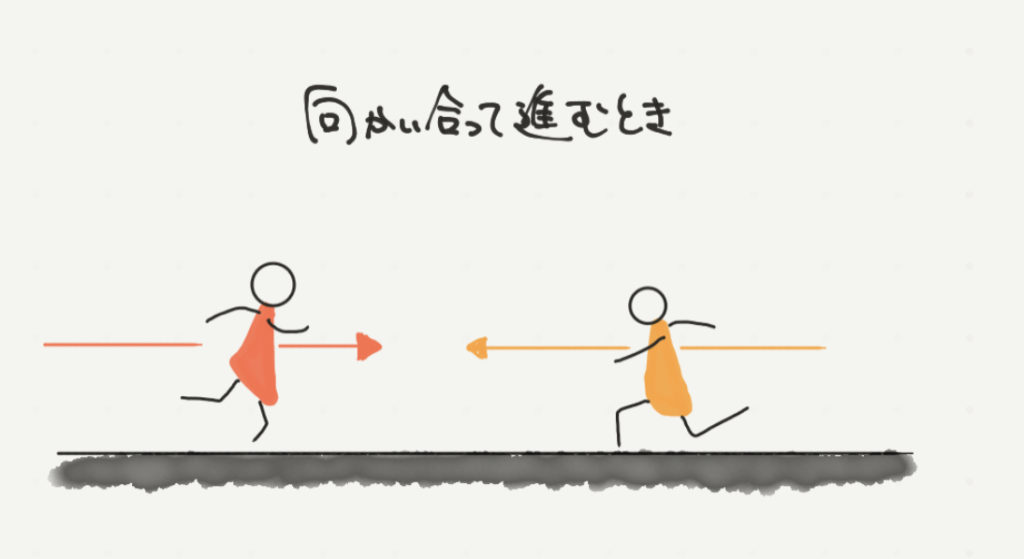
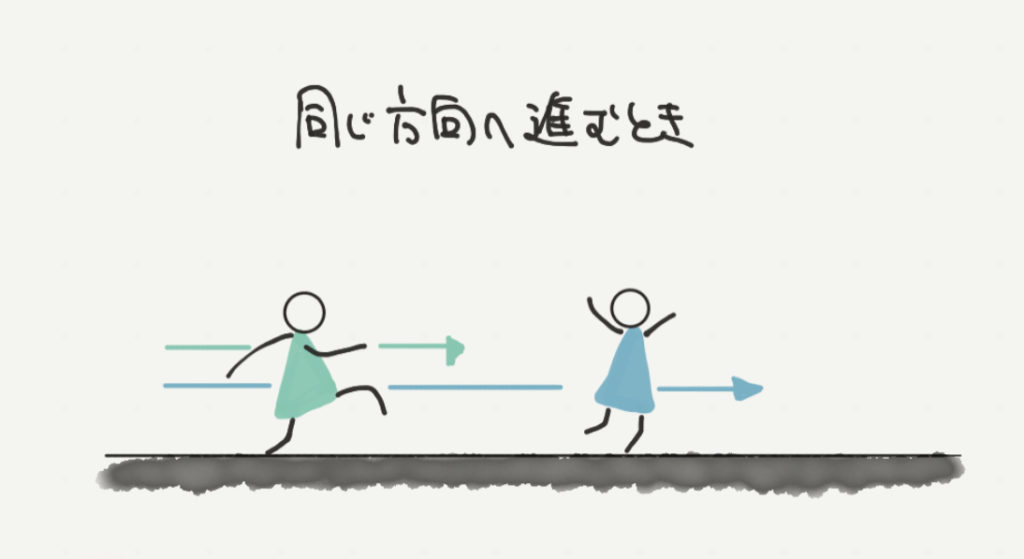
旅人算たびびとざんとは、違う速さで歩く人たちがいつすれ違ちがうのか、いつ追おい越こされるのかを求もとめるような問題です。
たとえば、ある2人が向かい合って進んだり、同じ方向を向いて進んだりという問題のことです。

受験でよく見かけるような問題ですよね。
今日はそんな「旅人算たびびとざん」の基礎きそ問題にチャレンジして行きましょう〜。

わからない受験生でも安心してください。
きちんとSTEP1から順番にご説明させていただきます！

↑ちなみに旅人たびとは？旅をする人のことです。どこかに旅行する人やある場所に向かっている人のことを旅人と言います。

問題に挑戦ちょうせん！

１km離はなれたA、B2地点を、一郎君は分速45mでA地点から、二郎君は分速80mでB地点から、同時に向かい合って出発しました。2人がすれちがうのは、A地点から何mのところですか。

解答

この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略こうりゃくしよう！

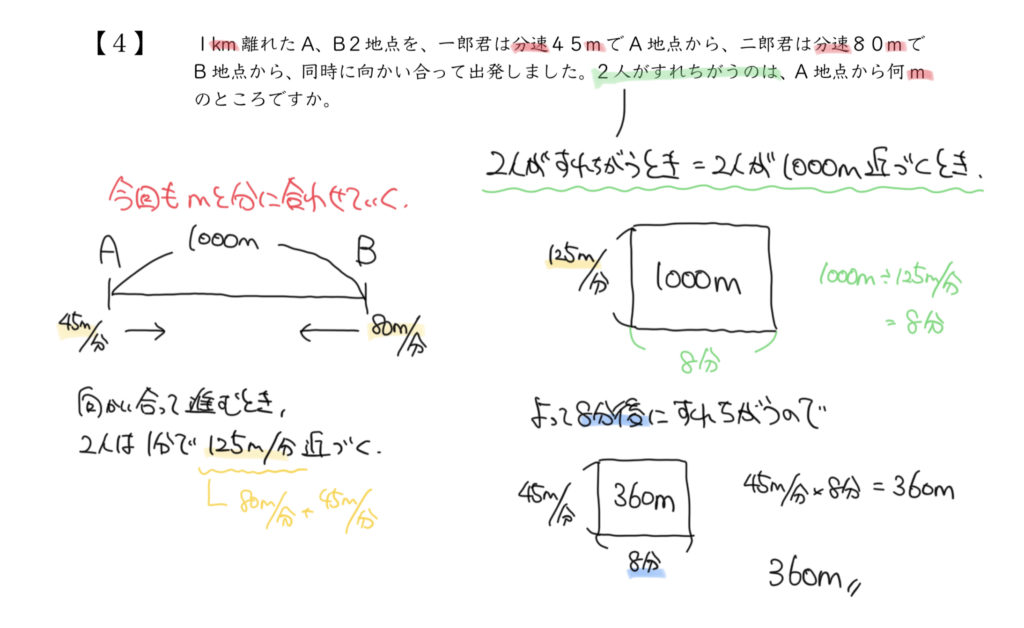
STEP1：単位をそろえてみよう

速さの問題では、図を書く前にまずは単位をそろえるように注意しましょう。
kmとかmとかを混まぜて計算してしまうと答えがおかしなことになってしまうので、必ず単位をそろえましょう。

今回は1kmと毎分45m、毎分80mなので単位を「m」にそろえると計算しやすいと思います。
なので、1km=1000mに直しておきましょう！

STEP2：問題文を図にしてみよう

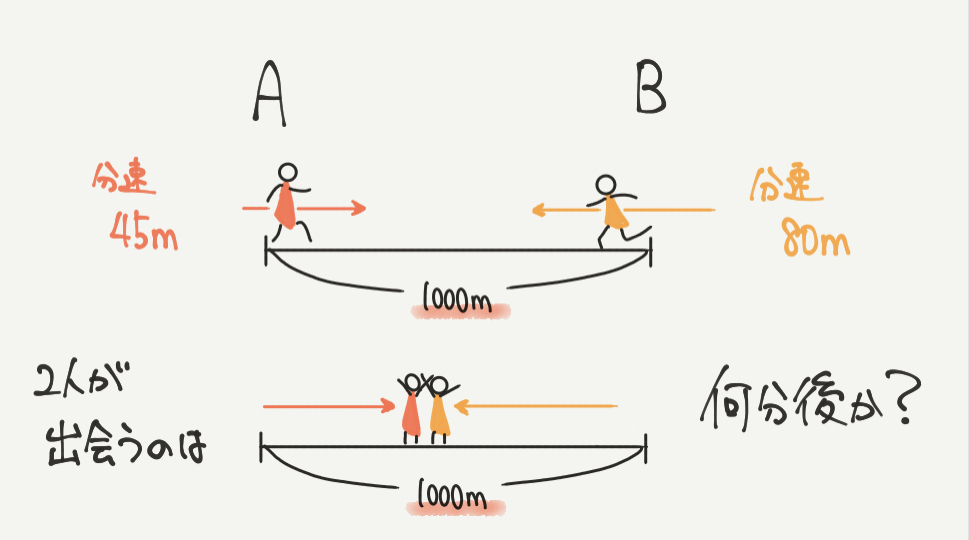
それでは問題文を図にしてみましょう。

最初はお絵かきしても大丈夫です。
上の解説も図というよりは絵ですね。

線分図を書いて、1000mはなれているところに一郎さん、二郎さんを書きましょう。
2人は向かい合って進むので方向（矢印やじるし）は→←と書くことができますね。

さて、2人が出会うのは何分後か、考えてみましょう。

STEP3：向かい合って進む＝1分でどれくらい近づくのか？

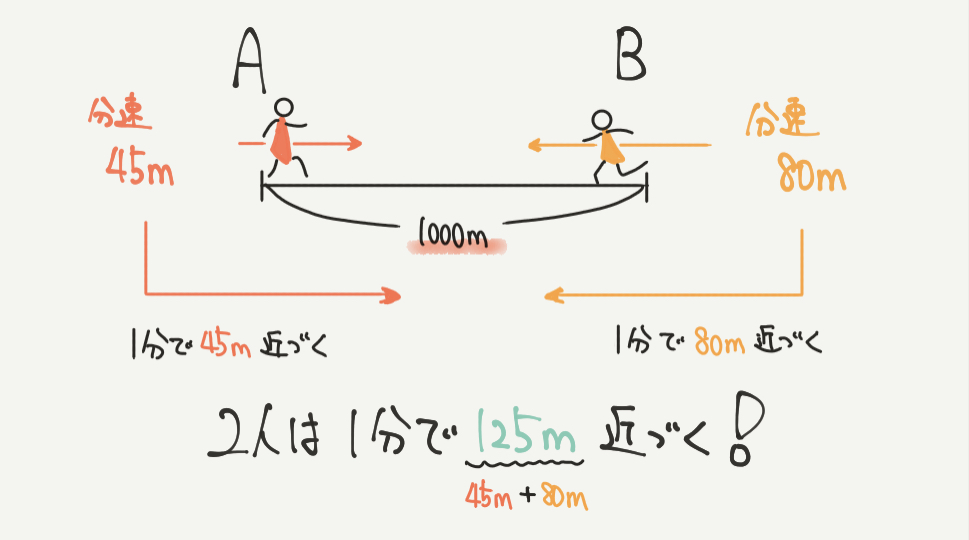
向かい合って進むとき、2人が1分でそれくらい近づくのかを考えましょう。

一郎さん＝分速45m（1分で45m進む）
二郎さん＝分速80m（1分で80m進む）

よって2人合わせて、
45m/分＋80m/分＝125m/分
1分間で125mずつ2人が近づくことがわかりますね。

STEP4：出会う＝2人の距離きょりが0mになるということ

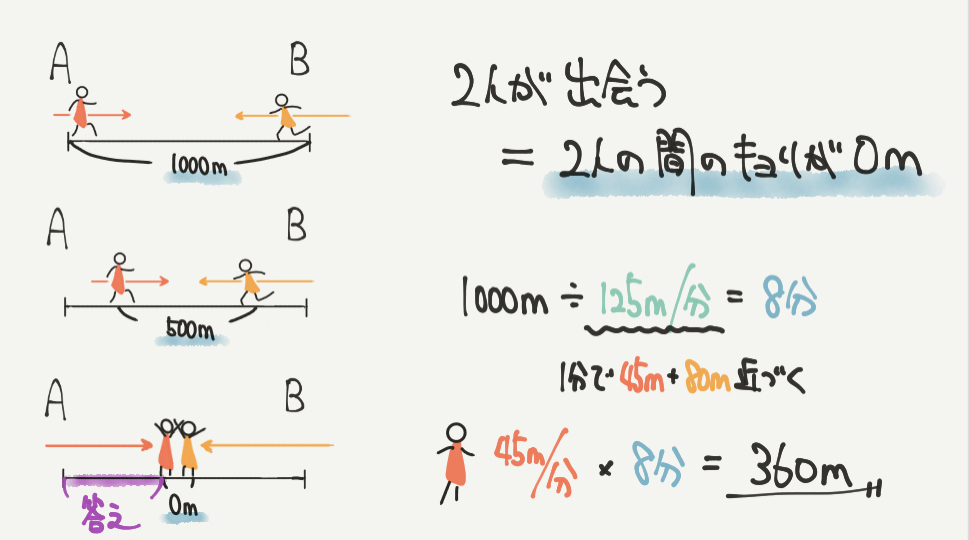
STEP3で2人は1000mはなれていて、1分で45m＋80m＝125m近くなることがわかりました。
ここから旅人算で大切な考え方を使っていきます！！

2人は1000mはなれている。（今）
2人の距離きょりは向かい合って進むのでどんどん短みじかくなる。（歩いているとき）
2人の間の距離きょりが0mになる。（出会うとき）

なので、2人が出会う＝2人が合わせて1000m近づいたとき！というのがわかります。
よって1000m÷125m/分＝8分と求めることができました。

最後に答えの部分を確認しましょう。
今回は太郎さんが進んだ距離きょりを知りたいので、
45m/分×8分＝360mが答えになります。

2人が向かい合って進むときのすれ違う時間を求める問題のまとめ

今回の問題で大事なポイント

速さの単位をきちんとそろえること（STEP1）
向かい合って進むときの考え方（2人の距離きょりが短くなっていく！）
2人が出会う＝2人の間の距離が0mになること！（STEP4）

さて、今回の「旅人算」の問題で大事だった考え方は

①速さの単位をきちんとそろえること
②向かい合って進むときの考え方（2人の距離きょりが短くなっていく！
③2人が出会う＝2人の間の距離きょりが0mになること！
の3点でしたね。

まだわからない受験生の方は、解説に書いてあるSTEP1,2,3,4を順番によく読んで、どこの解説部分がわからないのか確認しましょう。

たとえば、STEP2でうまく図が書けない受験生なら、「さんすうがく」のキーワード検索けんさくで「線分図」、「面積図」と調べればよりていねいな解説をたくさん見ることができます！

自分の弱点がどこにあるのかを知っていると、より効率的こうりつてきに勉強することができますので、ぜひ「さんすうがく」を使いこなしてみてください！！

その他の単元の問題の復習はこちらから！