はじめに
みなさんこんばんは!!
速さの問題で意外とパニックになってしまうのが歩幅と速さの比の問題です。
今までのような「旅人算」とは少し違い、速さの比ってそもそもなんだっけ?
といった部分から復習しておきましょう!
それでは勉強開始です!!!
速さの比=1歩歩く速さの比×歩幅の比
歩幅の比を求めてみよう
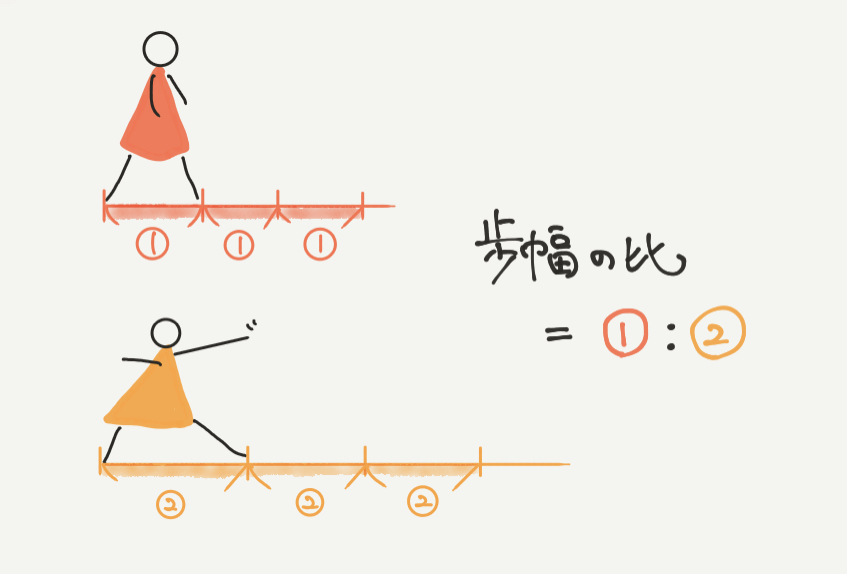
たとえば、赤い小人と黄色の小人がいたとします。
この絵の場合ですと、2人の歩幅(1歩進む距離)の比は①:②となります。
1歩歩く速さの比を求めてみよう
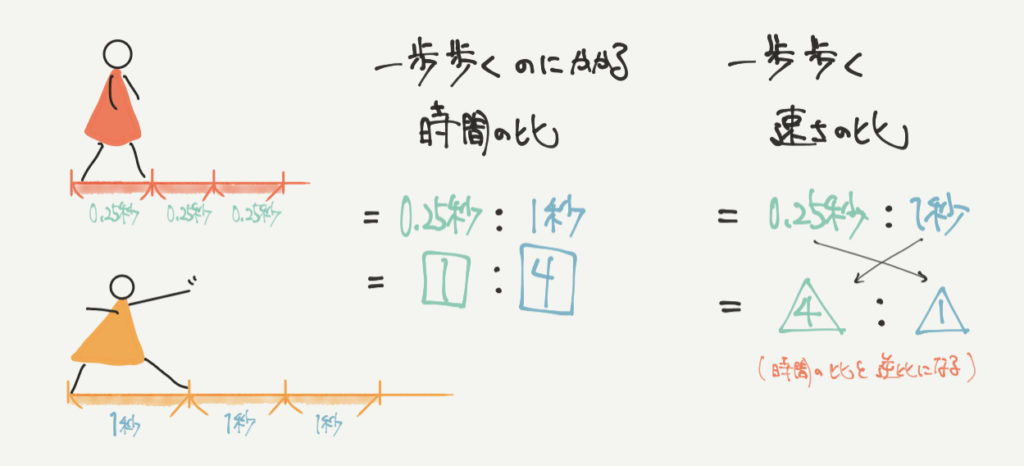
赤い小人は1歩を0.25秒で、黄色の小人は1歩を1秒で進むとしましょう。
このとき、2人が1歩歩くのにかかる時間の比は、
0.25秒:1秒=1:4になります。
ここからが大事です!!
1歩歩くのにかかる時間の比が1:4なので、
1歩歩くの速さの比は逆比の4:1になります。
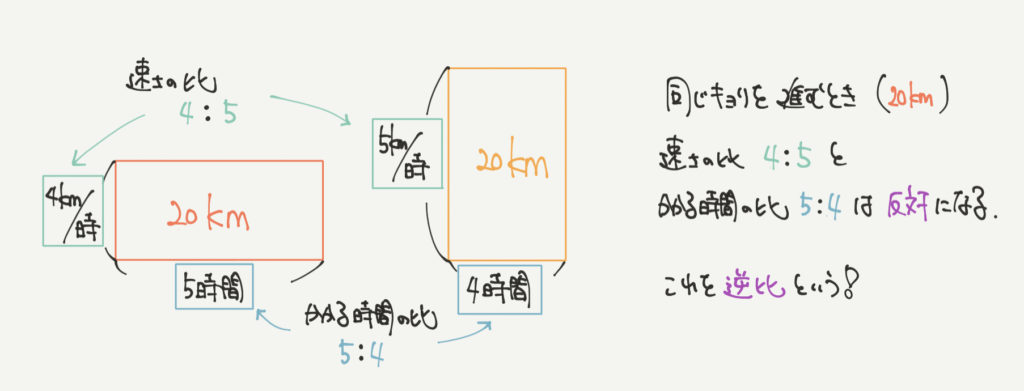
逆比の復習もしておこう
1歩歩く速さの比×歩幅の比(速さの比)を求めよう
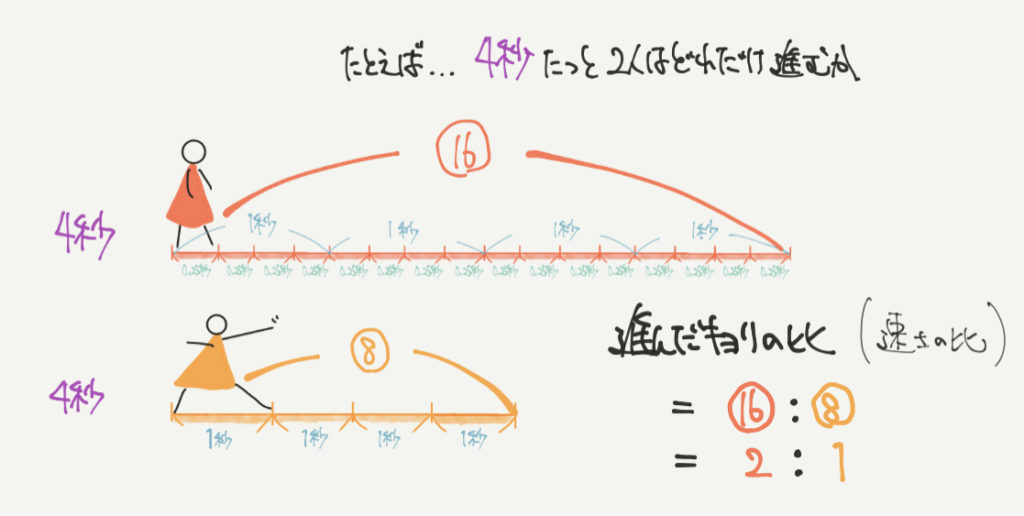
速さの比を求めていきます。
今回は「もし2人が4秒間歩いたらどれくらいの距離を進むのか?」と仮定して考えてみましょう。
すると赤い小人は⑯、黄色い小人は⑧だけ進むことができます。
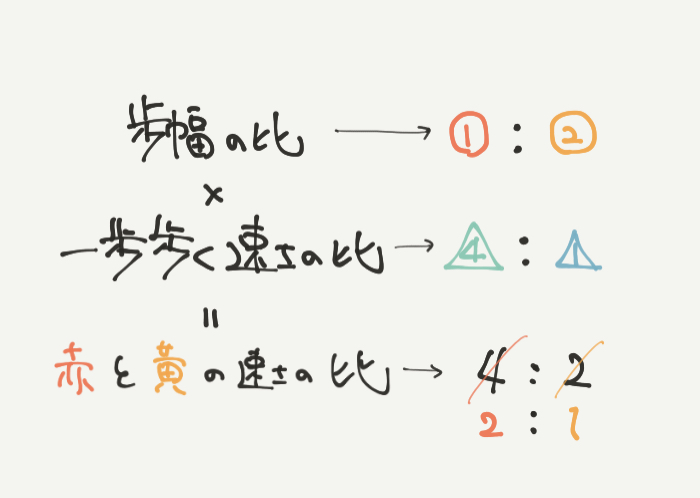
確認ですが、速さの比=1歩歩く速さの比×歩幅の比です。
よって赤い小人と黄色い小人の速さの比は
①×△4:②×△1=2:1となります!!
これは2人が同じ時間進む距離の比と同じになりますね!
(赤い小人は⑯、黄色い小人は⑧進む)
さて、だいぶ長くなってしまいましたが、これでやっと問題を解くことができます。
もう楽勝で解けるはずです!!さっそく解いていきましょう〜!
問題に挑戦!
解答
答えを見るにはここをクリック!
8:7
この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略
解説を見てみよう!
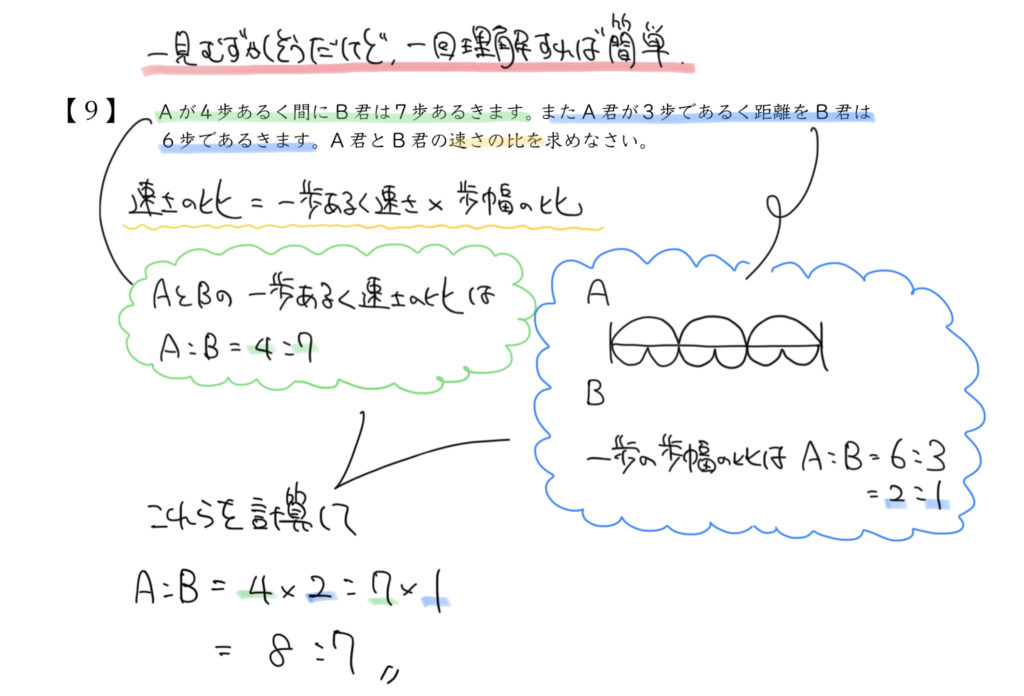
STEP1:問題文を図にしよう
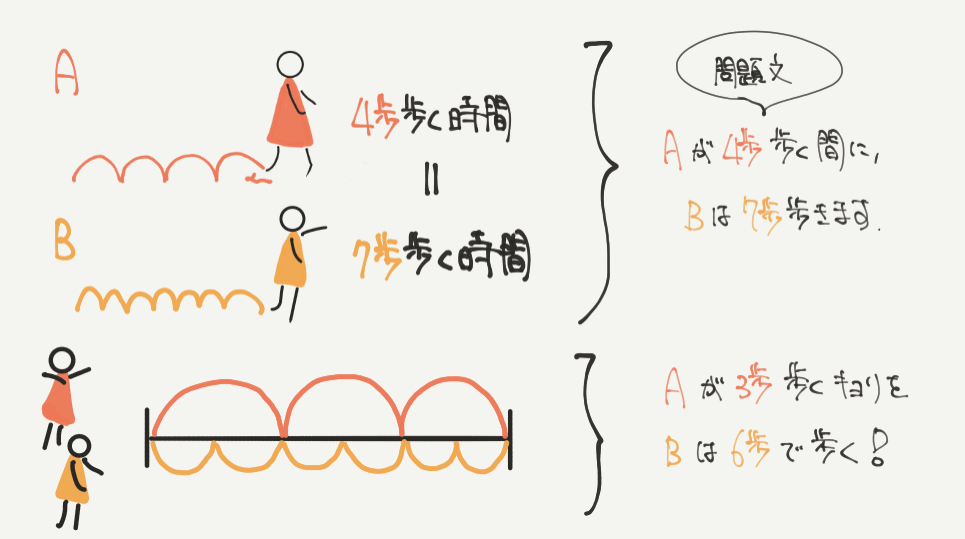
まずAとBの歩く時間を見ていきましょう。
Aが4歩で歩く時間と、Bが7歩で歩く時間が同じということ、
そしてAが3歩歩く距離をBは6歩で歩くことを図にしておきましょう。
別に図にしなくてもわかるよ!っていう受験生も頭の中でこのイメージができているかチェックしましょう。
STEP2:歩幅の比を求めよう
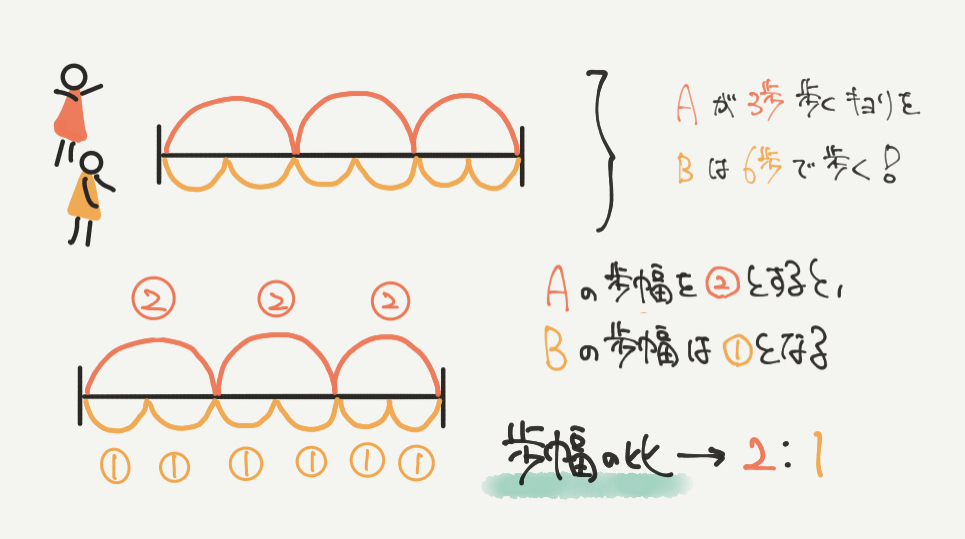
まずは歩幅の比を求めていきましょう。
Aが3歩歩く距離をBは6歩で歩きますので、上の図のような線分図を書くことができると思います。
ここで「仮定の考え方」を使っていきましょう。
今回は「もしAの歩幅が②だったら〜」と仮定して考えます。
すると、Aが3歩で歩く距離なので、全部で②×3歩=⑥進むことがわかります。
そして⑥進んだので、6歩歩いたBの歩幅は、
⑥÷6歩=①/歩となります。
よって歩幅の比は
A:B=2:1となります!
STEP3:1歩歩く速さの比を求めよう
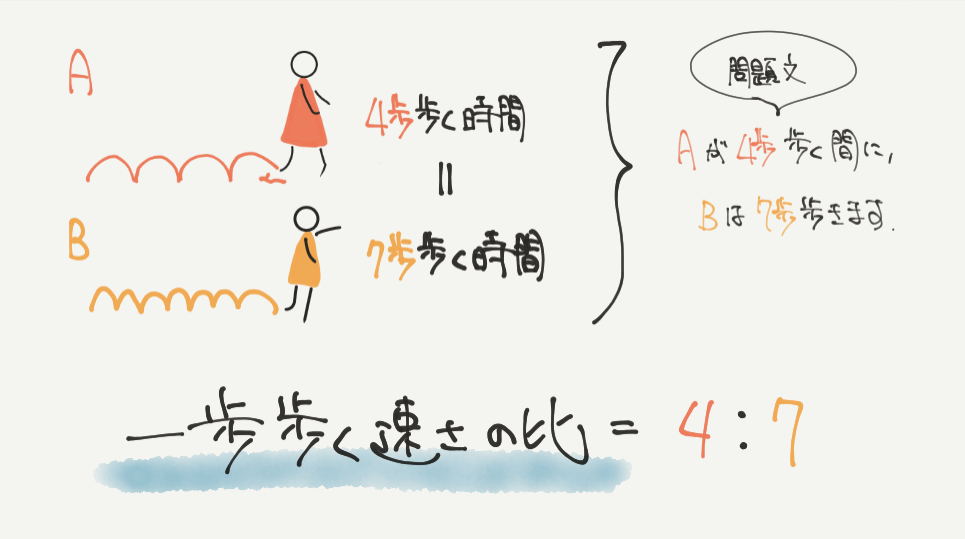
1歩歩く速さの比を求めるのは超かんたんです。
だって、Aが4歩歩く時間とBが7歩歩く時間が同じと言われているからです。
つまり1歩歩く速さはBの方がとてもはやいことがわかりますね。
なので、1歩歩く速さの比は、
A:B=4:7となります。
STEP4:速さを計算して求めよう
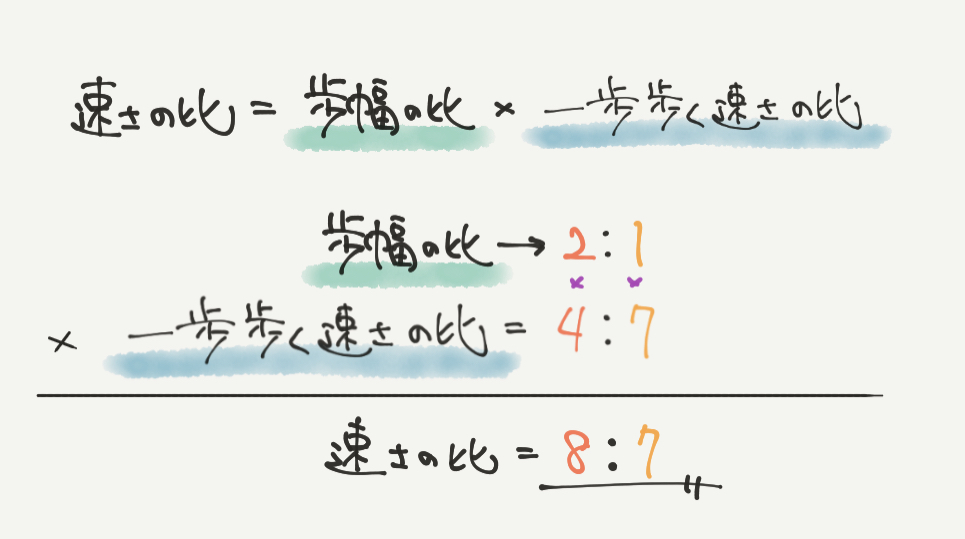
STEP3までできればあとは計算するだけです。
歩く速さの比は、一歩の速さ×歩幅の比で求めることができましたね。
まずはSTEP2で歩幅の比を、STEP3で一歩歩く速さを計算しました。
歩幅の比はA:B=2:1
1歩歩く速さの比は、A:B=4:7
よって2人の速さの比は、
2×4:1×7=8:7になり、答えを出すことができました。
歩幅と時間から速さの比を求める問題のまとめ
今回の問題で大事なポイント
速さの比=1歩歩く速さ×歩幅の比(はじめに)
仮定する考え方(STEP2)
・もし○○が□□だったら〜と考えること
長かった歩幅の問題もこちらでおしまいです!
おつかれさまでした〜。
歩幅の問題で大事だったのは、
①速さの比=1歩歩く速さの比×歩幅の比ということ!
②仮定する考え方(「もし○○が□□だったら〜」と考えること)
の2つでした。
とくに、①の速さの比=1歩歩く速さの比×歩幅の比の考え方は知っていればかんたんに解ける問題にもなっているので、ぜひ復習するようにしてください。
知っているだけで問題が解けるのはラッキー問題です!
1つ1つ知らない問題をなくしていくために、「さんすうがく」では受験でたくさん出るような問題の他にも受験であまりでない、めずらしい問題ものせています。
どんどん問題を解いて勉強していきましょう〜!