はじめに
みなさんこんばんは!!
今回も「旅人算」の問題にチャレンジしていきましょう。
他の「速さ」の問題とも少し違う問題ですので、ぜひ試しに解いてみてください〜!
走る時間と走った距離は比例の関係になっている
実際に走った距離の比を計算してみてみよう!
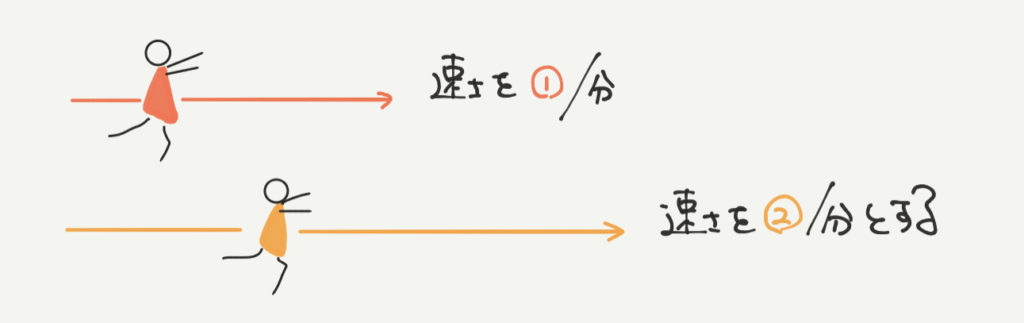
例えば、赤い小人と黄色い小人がいたとします。
2人の走る速さはそれぞれ①/分と②/分の速さで走ります。
このとき、2人の走る速さの比は①:②=1:2となりますね。
さて、ここで2人が同じ時間だけ走ったときの距離を求めてみましょう。
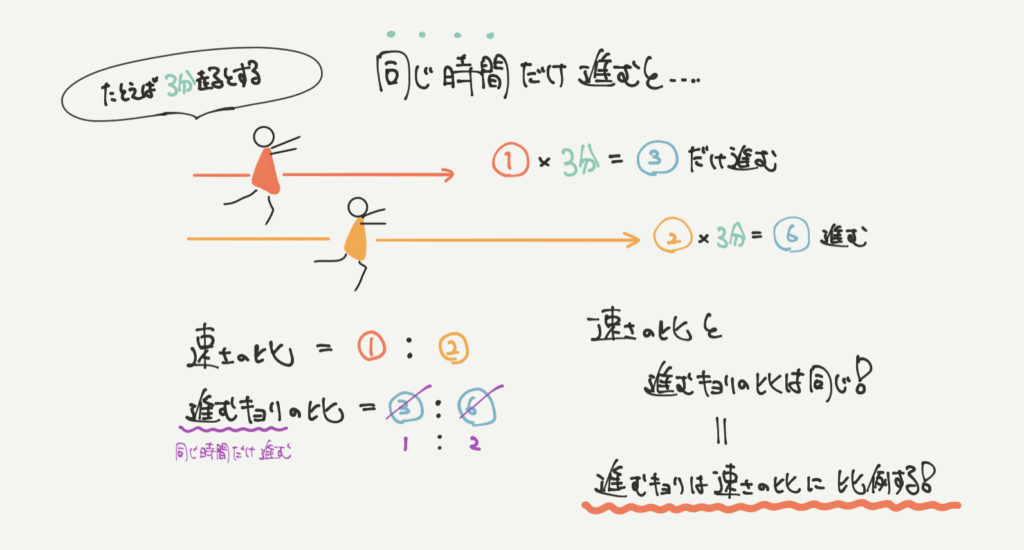
3分間2人が走るとすると、
2人が進んだ距離は、
赤い小人:①×3分=③
黄色い小人:②×3分=⑥
となります!
よって進んだ距離の比は、
赤:黄=③:⑥=1:2となりますね。
なので、同じ時間だけ進んだとき、
速さの比と進んだ距離の比が比例することがわかりますね。
それではこちらの内容をふまえて、問題に挑戦です!
問題に挑戦!
解答
答えを見るにはここをクリック!
25分
この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略
STEP1:問題文の内容を図にしよう
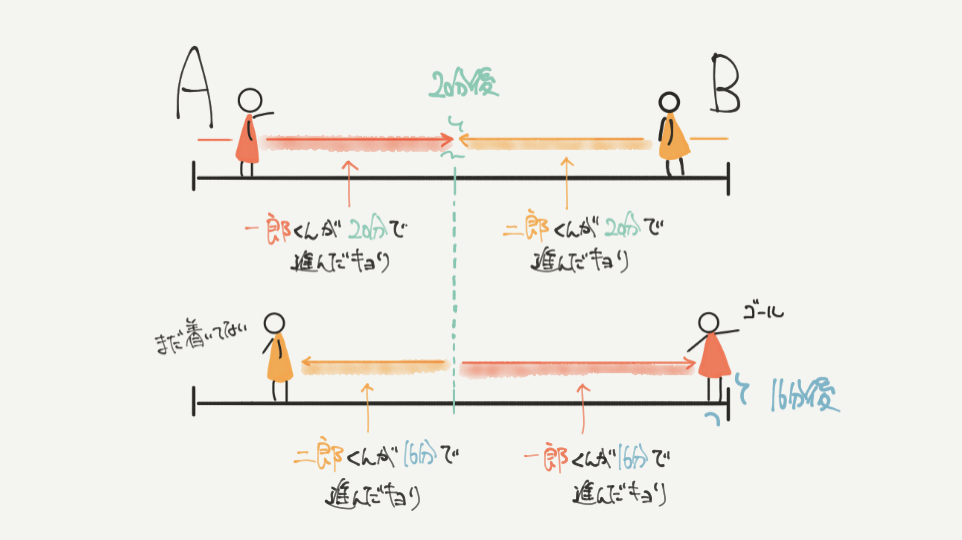
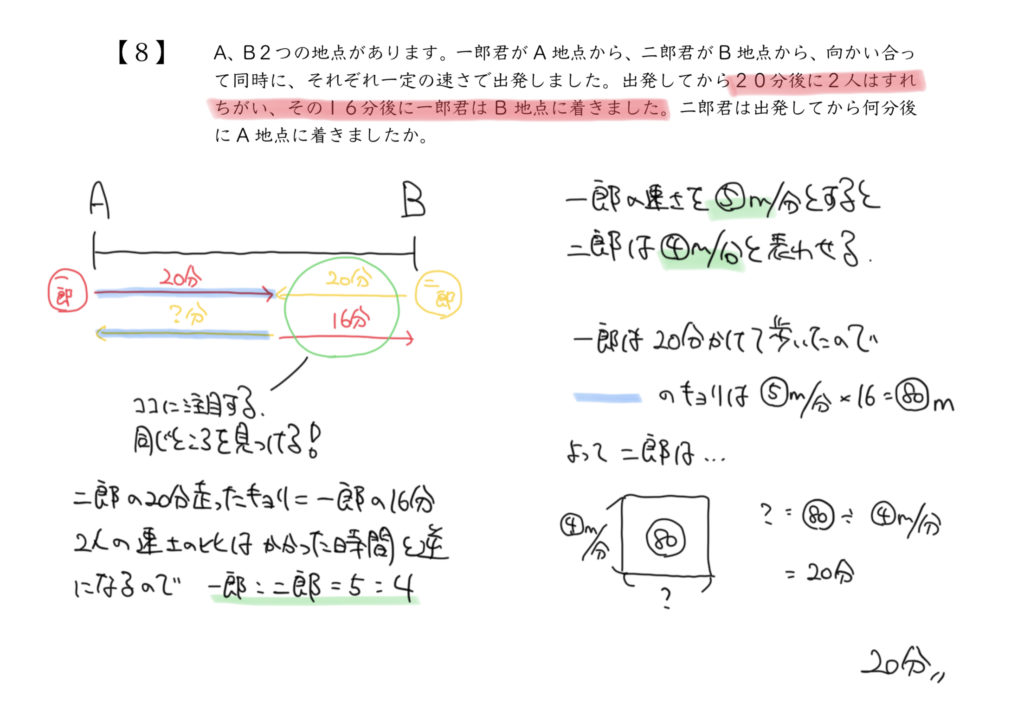
まずは線分図を書いて、問題文の内容を図にしていきましょう。
解説図ほどていねいに書く必要はないですが、今回大切になってくる部分は
だれが、どれくらいの時間進んだ距離なのか?ということです。
たとえば、解説の図には
左上:一郎くんが20分かけて進んだ距離
右上:二郎くんが20分かけて進んだ距離
左下:二郎くんが16分かけて進んだ距離
右下:一郎くんが16分かけて進んだ距離
の4つの距離が出てきています。
このように線分図を理解しながら問題を解いていきます。
STEP2:同じところを見つけていこう
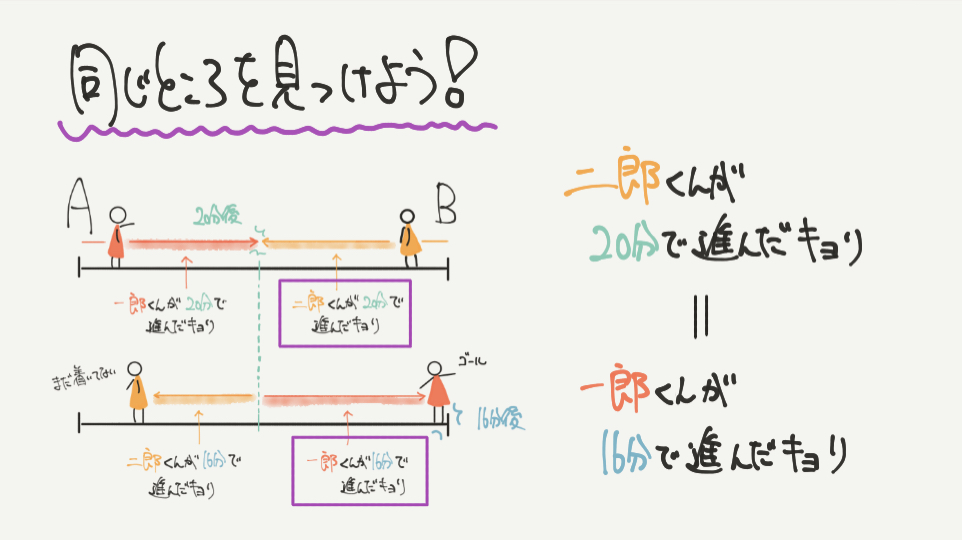
さあ!図を書いたら線分図から同じところを見つけていきましょう。
今回わかる同じところは、
二郎くんが20分かけて進んだ距離=一郎くんが16分かけて進んだ距離
となります。
ここまで分かればSTEP3へ進んでみましょう!
STEP3:進んだ距離が同じとき、かかる時間の比と速さの比は逆比になる!
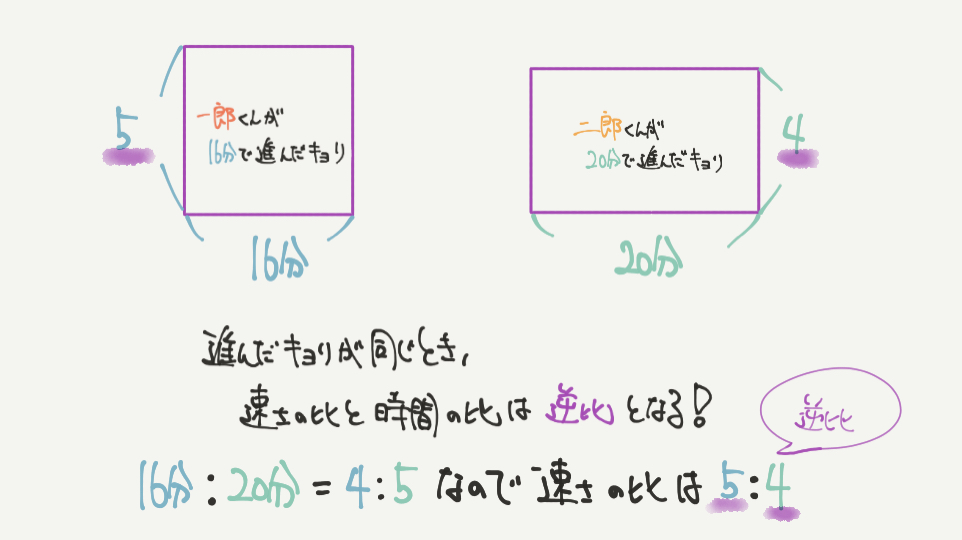
さて、ヒントでは、「走る時間と走った距離は比例の関係になっている」と説明しました。
今回はそれの反対の考え方です。
「走る時間はわからないけど、走った距離が同じときの関係」について考えてみましょう。
進んだ距離が同じ場合、速さの比とかかった時間の比は逆比の関係になります。
よってかかる時間の比(4:5)から、2人の速さの比は逆比の5:4となります。
走った距離が同じときの速さの比を計算してみよう
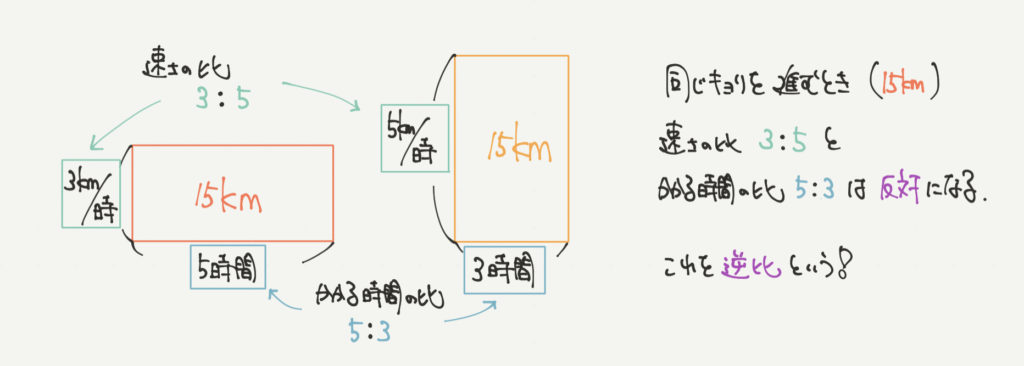
たとえば、15kmを走るとき
速さの比は3km/時:5km/時=3:5となりますね。
反対に、かかる時間は5時間と3時間なので
5時間:3時間=5:3と求めることができました。
このように速さの比と、かかる時間の比は反対になります。
これを逆比と言います。そして今回の問題の解説ではこちらの逆比の考えが出てきました。
STEP4:逆比を使って答えを出していこう
1つ1つていねいに考えていきます。
ゆっくり解説していくのできちんと理解してから、復習していきましょう。
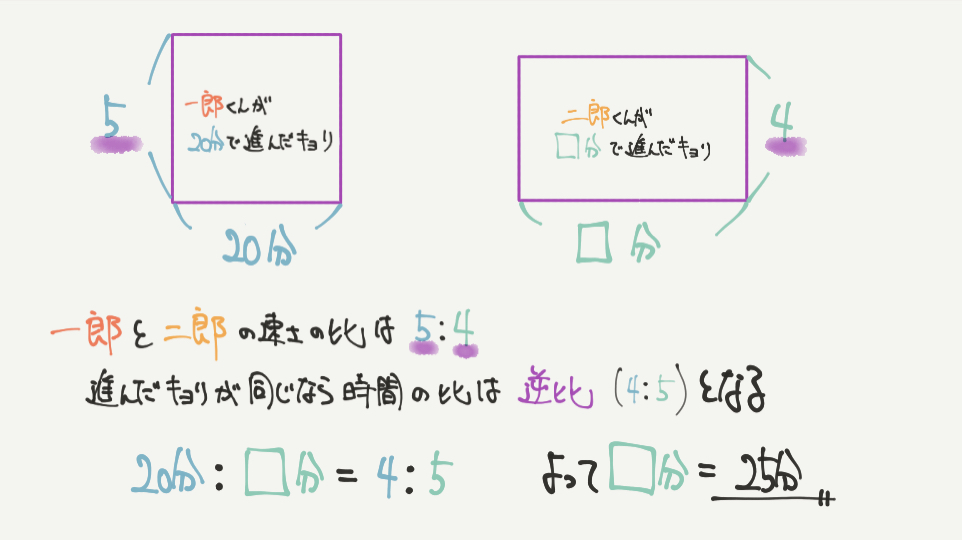
STEP3から一郎と二郎の速さの比が5:4と求めることができましたね。
進む距離が同じなので、かかった時間の比は逆比の4:5となるはずです。
20分(一郎くんの進んだ時間):□分(二郎くんの進んだ時間)=4:5となるので、
□分=25分と求めることができました。
2人の歩いた時間から距離を求める問題のまとめ
今回の問題で大事なポイント
進んだ時間が同じなら、進んだ距離の速さに比例する
逆比の考え方(STEP3、4)
今回のポイントとしては、
①進んだ時間が同じなら、進んだ距離は速さに比例する
②逆比の考え方
の大きく2つがありましたね。
もちろん、他の解き方で考えても問題を解くことはできます。
自分が解きやすいやり方を探して、楽に問題を解いていけるようにたくさん復習しておきましょう〜!
比例、反比例の問題の復習
表から比例と反比例を求めるには?
逆比の考え方の復習
歯車の歯数から回転数を求めるには?