はじめに
受験生のみなさん、こんにちは!
今日は中学受験算数の「割合と比」の問題について勉強していきましょう。
今までの割合の問題だけでなく、新しい逆比という考え方が出てきます。
まずはこの逆比についてから勉強して、問題に挑戦していきましょう!
逆比ってなに?
一言で言うと逆比とは、ある2つの数の逆数の比のこと、です。
これだけだと全くわからないと思うので、カンタンな例からみていきましょう。
逆数のカンタンな例を考えてみよう
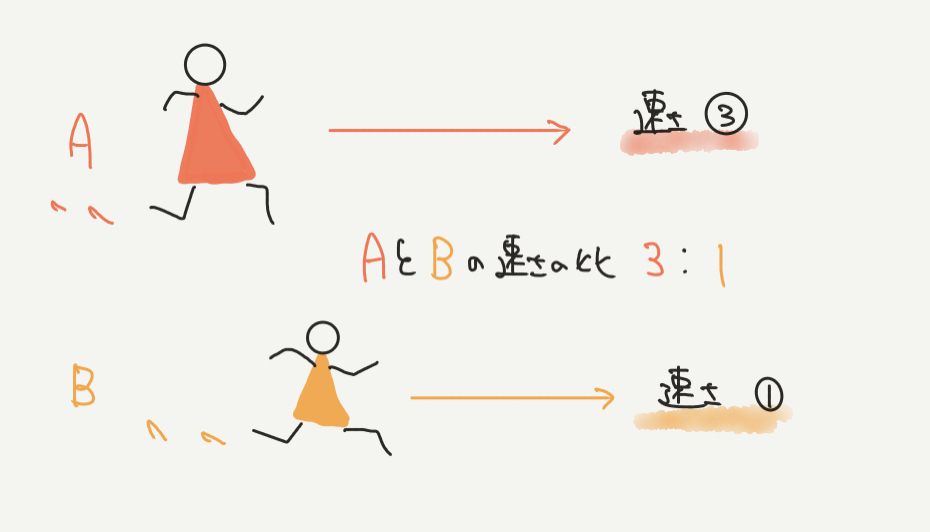
たとえば、AさんとBさんがいたとします。
Aさんの走る速さは③、Bさんの走る速さを①とすると、2人の走る速さの比は3:1になります。
逆比のポイント
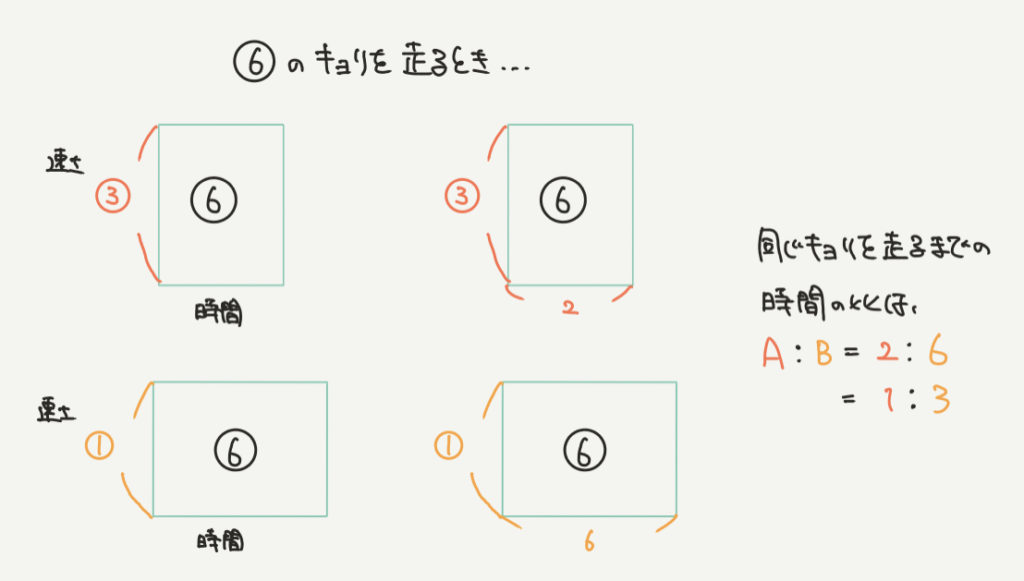
この2人が同じ距離を走るとき、たとえばAさんとBさんが⑥の距離だけ走りたいとすると、
かかる時間は、
Aさん:⑥÷③=2
Bさん:⑥÷①=6
となりますね。
よって同じ距離だけ走るときにかかる時間の比は、
A:B=2:6で、A:B=1:3、となります。
走る速さとかかる時間が逆比になる!
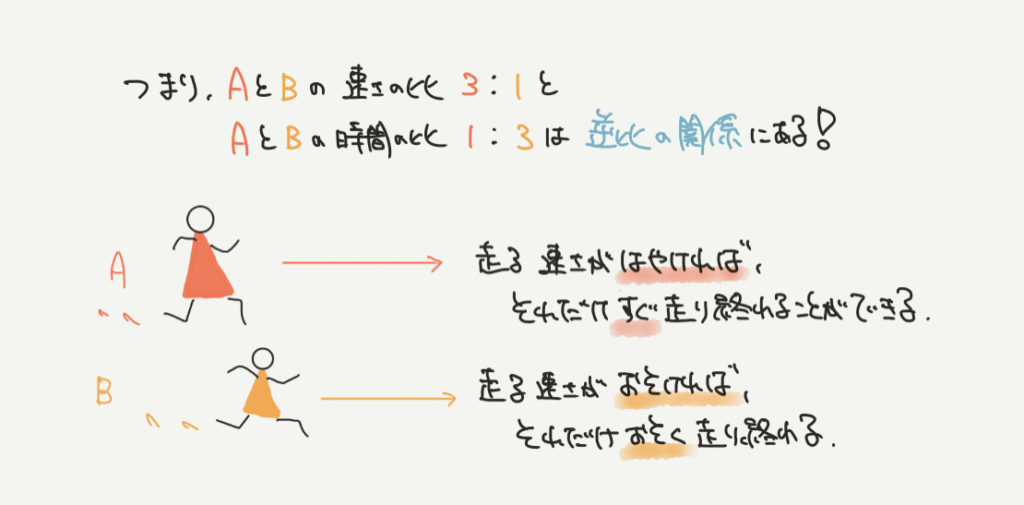
さっきまでの内容をまとめると…
AとBの速さの比=3:1
AとBの時間の比=1:3
というように比が反対になります。
これを逆比といいます!!
逆数の復習はこちらから!!!
共通している部分の割合から全体の比を求めるには?

実は↑の問題でも逆比の考え方が出てきます!
見つけられるかチャレンジしてみてください!!
問題に挑戦!
解答
答えを見るにはここをクリック!
70回
この記事を書いている人はこんな人


解説を読んで「 割合と比 」を攻略しよう!
STEP1:歯車にも逆比がある!?
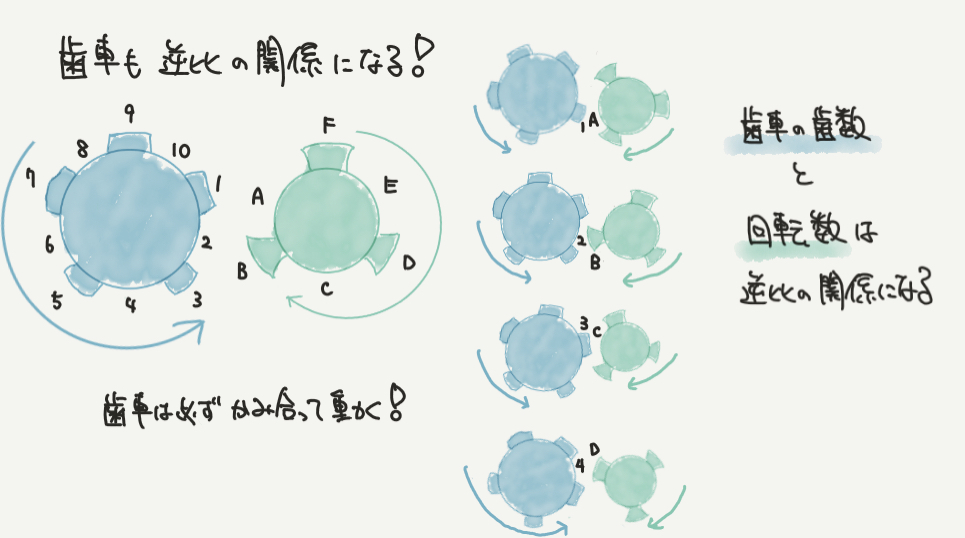
解説にも書いてあるとおり、歯車の問題でも逆比があります!
歯車はかみ合ってまわるというところがポイントでした。
たとえば青の歯車と緑の歯車があったとしましょう。
それぞれの歯とすきまを1,2,3,4,5,6,7,8,9,10とA ,B ,C ,D ,E ,Fと書いておきます。
これらの歯車は必ずかみ合って動くので、絵のように青の1と緑のAがかみ合います。
同じように青の2と緑のBがかみ合い、青の3と緑のCがかみ合いながら回転します。
STEP2へ続く…
STEP2:歯数と回転数が逆比の関係
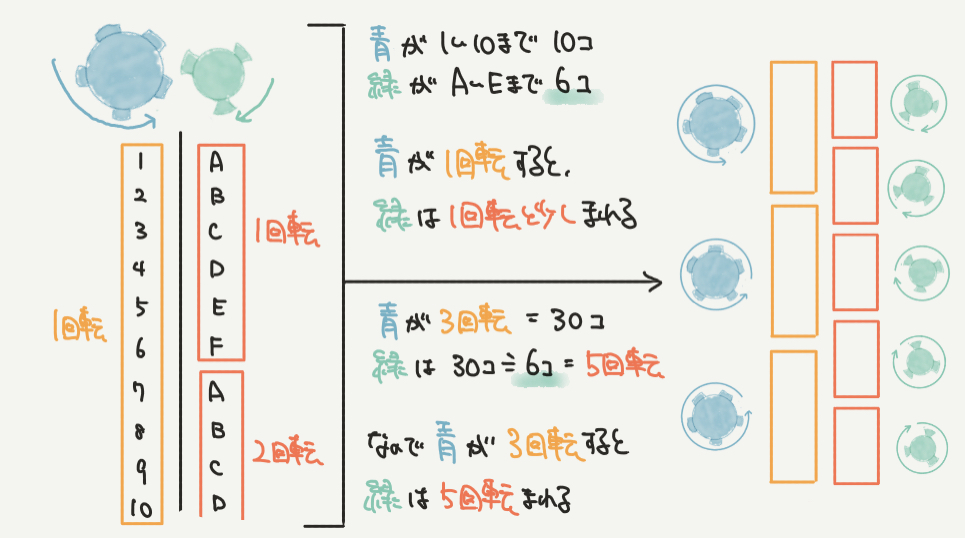
すると、青が1回転するまでに歯とすきまは1から10まで動き、緑はABCDEFとABCDの1回転と少し回転することがわかります。(左の図!)
それぞれの1回転するまでに、青は1~10の10こ、緑はA~Fの6こ動く必要があるので、
青が3回転(10こ×3回転=30こ動く)するとき、緑は5回転(6こ×5回転)することがわかります。
ここから、歯車の歯数(青の歯数は5、緑の歯数は3)と回転数の比(青が3回転すると緑は5回転する)は逆比の関係にあることがわかります!!
少しわかりづらいですが、理解できましたでしょうか。
ここまでわかればあとはすぐに答えが出ます。
STEP3:問題文の内容を図にしよう
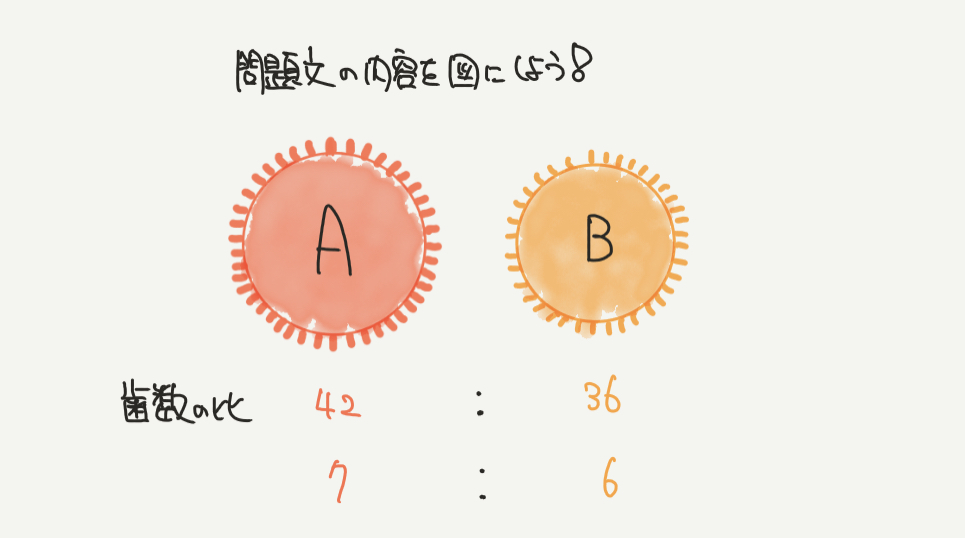
実際の問題ではここまできちんと図を書く必要はないですが、
今回はていねいな解説なのできちんと歯数を42、36で書いてみました。
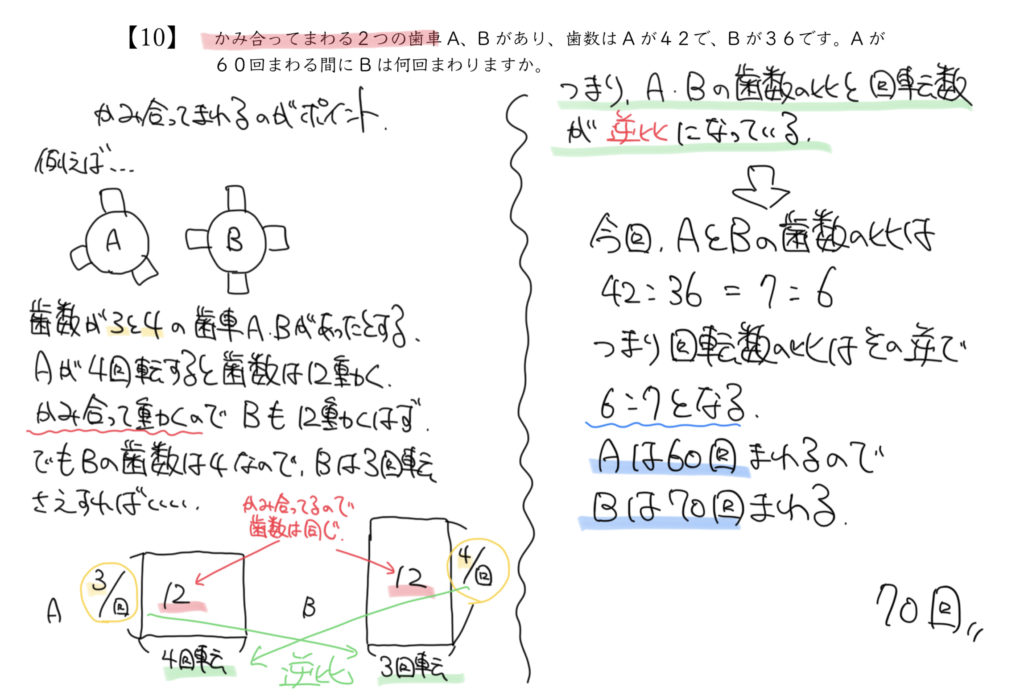
ここから歯数の比が42:36、両辺を6で割って、
歯数の比=7:6であることがわかります。
STEP4:あとは逆比で解くだけ!
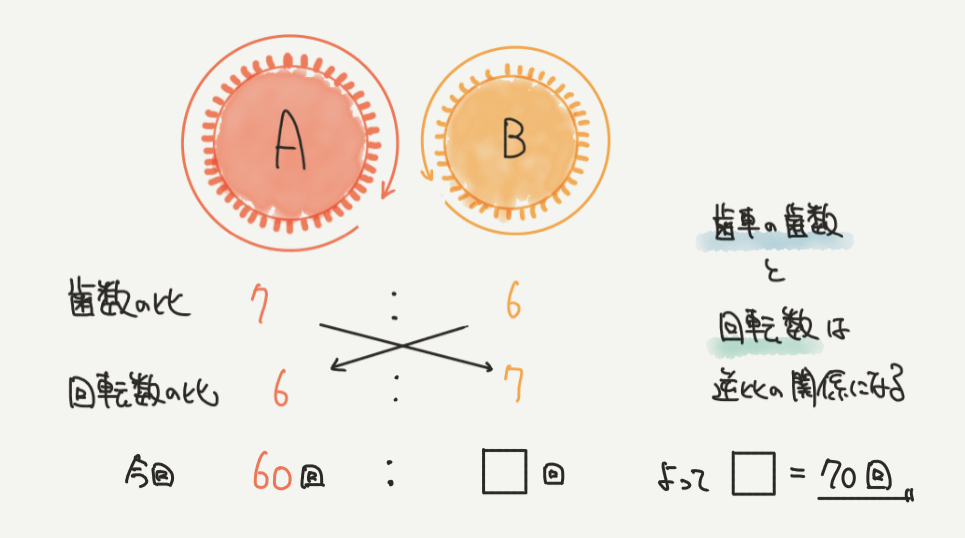
歯数の比と回転数の比は逆比になるので、
回転する比は6:7(7:6の反対)になります。
今回Aが60回回転するので、回転数6:7より、
Bは70回転することがわかります。
逆比に関する説明はこちら↓でもしているので、ぜひ復習してみてください!
割合と比の復習
割合と比〈攻略法〉

歯車の歯数から回転数を求める問題のまとめ
今回の問題で大事なポイント
逆比の考え方(STEP1、2)
歯車の考え方(STEP1、2)
・歯車はかみあって動く!
以上、歯車と逆比の問題でした。
少しむずかしかったと思いますが、きちんと理解することができたでしょうか?
歯車の問題に限らず、大事だったのは上の
①逆比の考え方
②歯車の考え方
と言う2点でしたね。
逆比の考え方は以前勉強したように、走る速さの比と走るまでにかかる時間の比を考えてもらうとわかりやすいと思います!
少しでもわかりづらいところがあれば遠慮なくコメントで教えてくださいね!
特にSTEP2のイラストは内容がもりだくさんだったので、むずかしいところがあったと思います。
なるべく受験生の皆さんが理解できるよう、引き続きがんばって解説をかいていきますので、
みなさんも一緒にがんばりましょうね!!