はじめに
みなさんこんばんは!!
今日も「速さ」の問題を解いて解いて解きまくりましょう!
同じようで、少し違う今回の問題、果たして正解できるでしょうか?
一発で正解できたらきちんと今までの「速さ」の問題が復習できていると思います。
それではいつも通り、ヒントから見ていきましょう。
楽に問題を解いてみよう!
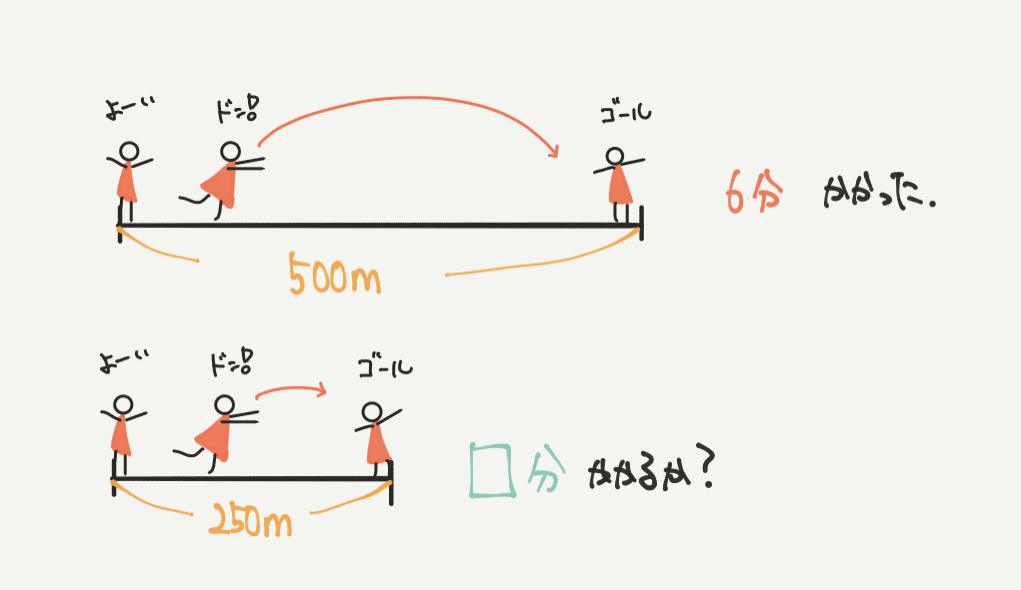
たとえば、赤い小人が500mを6分で走ったとします!
このとき、250mを何分で走ったのかを求めてみましょう。
やってはダメな計算方法
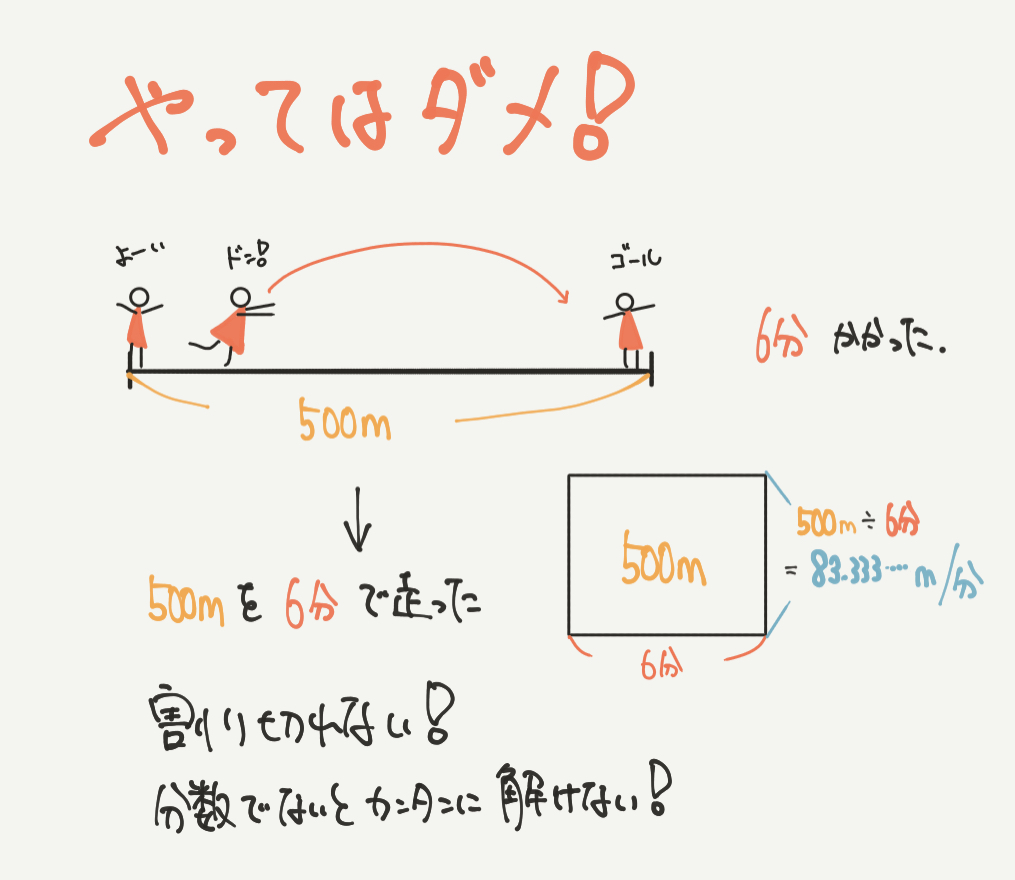
まずはやってはいけない解き方を紹介します。
今回のやってはいけない解き方は、
6分で500m走ったので、
1分間で何m走ったのかを計算することです。
なんで1分間で走った速さを求めてはいけないのか?
別に求めてはいけないわけではないのですが、
テストで解くときに時間がかかってしまうのでやめておきましょう、ということです。
今回の問題で分速(1分間に進む速さ)を求めてはいけない理由は、数が割り切れないからです。
500m÷6分=83.3333•••m/分となってしまい、これでは計算ができませんね。
分数を使って計算できますが、それでも時間がかかってしまいます。
かんたんなやり方で走った距離を求めよう
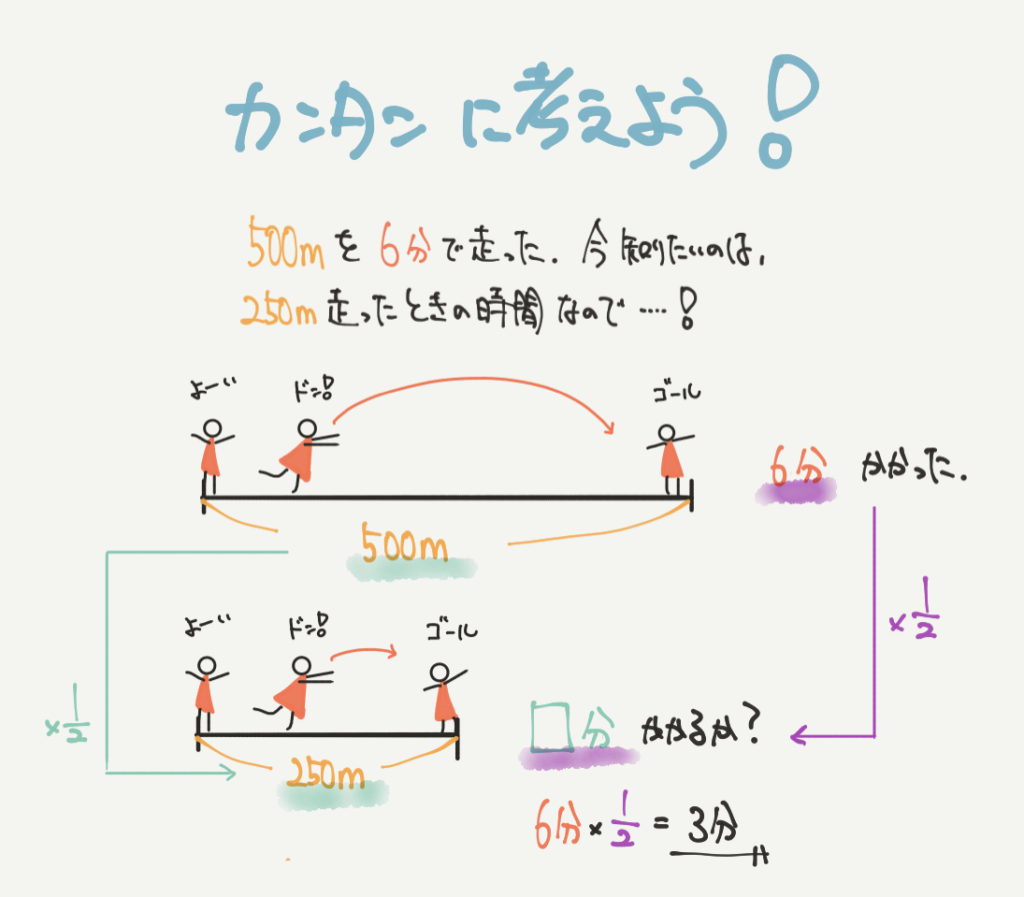
今回知りたいのは赤い小人の分速(1分間で進んだ速さ)ではありません。
今回知りたいのは250mを何分で走るのかということです。
なので、分速を求めなくても実はかんたんに答えを出せます!
走る時間と走った距離は比例する
500mを6分で走ったので、半分の距離の250mは、半分の時間の3分で走ったことになります。
これは走る時間と走った距離が比例しているからです。
長く走れば走るほど、遠くへ進むことができますね?これが比例の考え方です。
逆に同じ距離を早く走れば走るほど、かかる時間は短くなりますね。これを反比例とよびます。
ここまで分かれば、今回の問題は楽勝です!!!
さて、やっていきましょう!
問題に挑戦!
解答
答えを見るにはここをクリック!
5m
この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略しよう!

STEP1:問題文を図にしてみよう
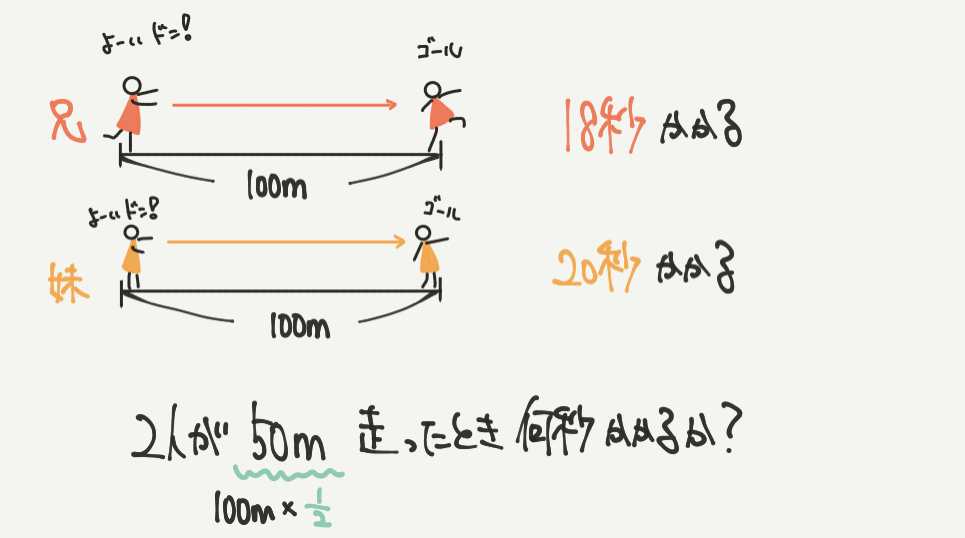
まずは問題文を図にします。これは「さんすうがく」ではいつも通りの解き方ですね。
ここまでていねいに書かなくても、イメージがきちんとできていればOKです。
兄は100mを18秒
妹は100mを20秒かけて進みます。
問題文では50mの距離を走っているので、50mを走る時間を求めていきましょう。
STEP2:兄と妹が50m走るときにかかる時間を求めよう
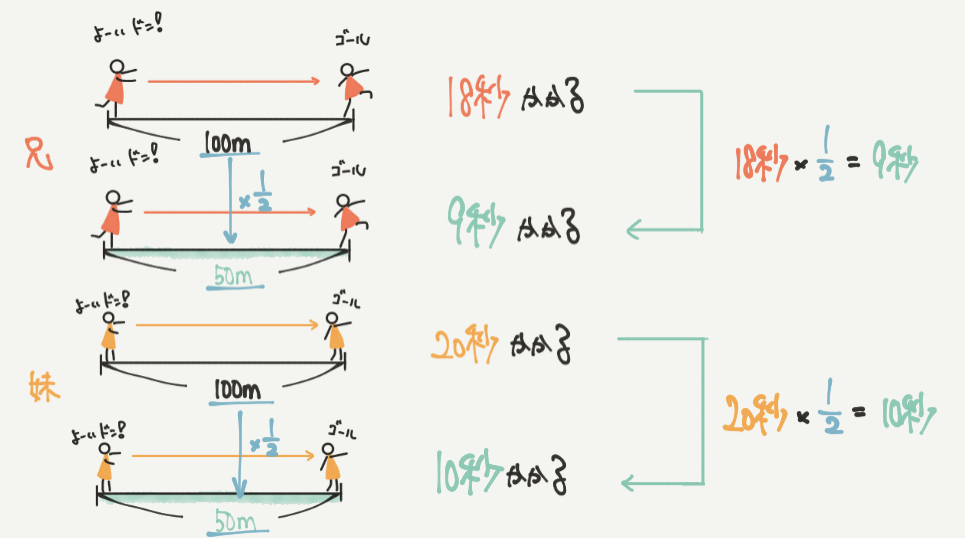
兄と妹が走る距離は100mから50mへ×1/2(半分に)されています。
よって兄が50mを走る時間は、
18秒×1/2=9秒
そして妹が50mを走る時間は、
20秒×1/2=10秒、と求めることができますね。
STEP3:兄がゴールしたときを考えよう
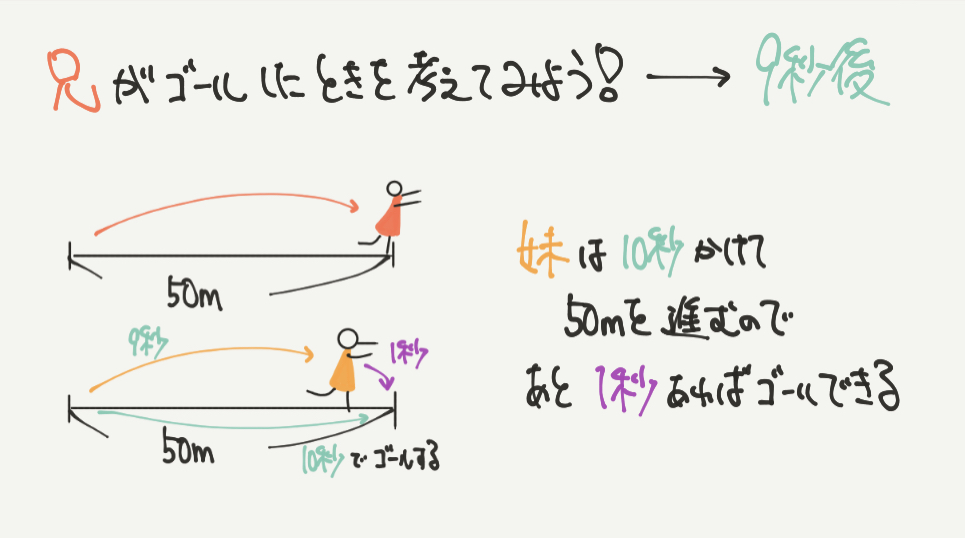
問題文から、まずは兄が先にゴールすることがわかると思います。
なので兄がゴールしたとき、つまり9秒後の瞬間をみてみましょう。
9秒後では兄がゴールしており、妹が後ろを走っている状態です。
さて、ここで妹の速さに注目です。
妹は10秒で50m進むことができますが、まだ9秒しかたっていません。
なので、妹はゴールするために、
10秒–9秒=1秒の、あと1秒間走る必要があります。
つまり妹は、1秒間で進む距離だけゴールから離れていることになります!
STEP4:妹が1秒間で進む距離を求めよう
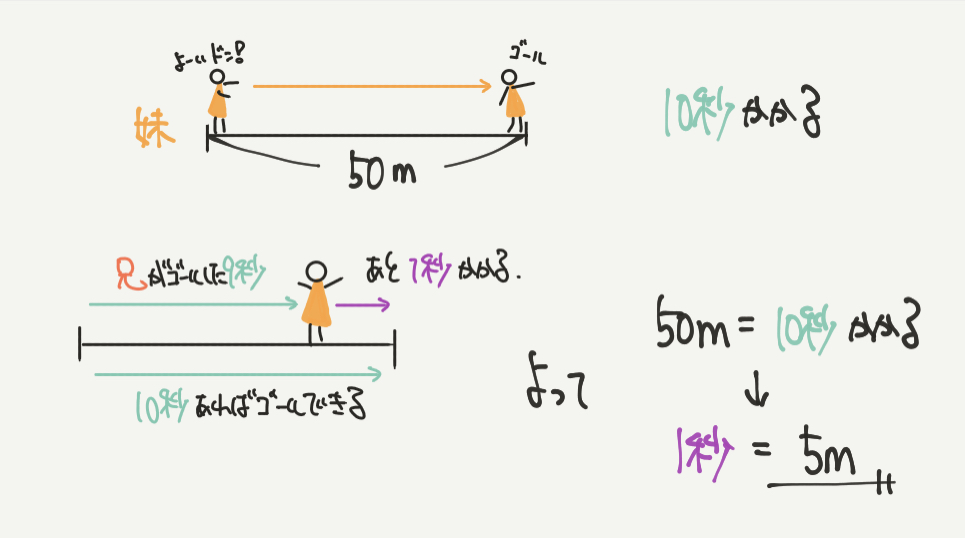
STEP3までできれば、あとはかんたんです。
妹は100mを20秒、
50mを10秒かけて進むので
1秒あれば、
50m÷10秒=5m/秒(1秒間で5m進む)ということがわかります。
よって妹は兄がゴールしたとき、5m後ろを走っている、が答えです!
1人がゴールした時、もう1人が何m後ろにいるか求める問題のまとめ
今回の問題で大事なポイント
計算は楽をして考えよう!(STEP2)
線分図の書き方(STEP1、2、3、4)
・問題文の内容をきちんと図にしてみよう
この問題ではシンプルに考えることが大事だったと思います。
いつもなら秒速や分速を求めて計算してしまいますが、必ずそのやり方が正解というわけではないです。
今回の問題のように場合によっては計算しないほうが楽に解ける場合もあります。
受験でパニックになる問題かも!
これは私の経験した話ですが、やったことありそうだけどいつもと何か違う問題、というのは受験においてパニックになりやすい問題だと思います。
速さの問題だから解ける!と思ってもこの問題はいつもの速さとは少し違うので、
解き方がわからない、図が書けない、割り切れない数になってしまう!と、パニックになってしまいます。
そんなときは一回落ち着いて、ゆっくり、深呼吸しましょう。
解説を見るとすごくかんたんな問題だったと思います。
少なくとも絶望するほどむずかしい問題ではなかったですよね?
このようなパニックにならないためにも、
①色々な問題を受験前に解いておくこと
②わかりそうでわからない問題が出ても落ち着くこと
を意識しておきましょう。