はじめに
みなさんこんばんは!!「さんすうがく」の赤い小人です。
今日は中学受験算数の「時計算」について勉強していきましょう!!
時計算のヒントを復習しよう
時計には長針と短針がありましたね。
長針は時計の長い針のことで、短針は時計の短い針のことでしたね!
まずは長針の進む速さから確認しましょう!

時計の長針は1時間で1周しますので、1分で6°進むことになります。
なのでイメージとしては長針(図の赤い小人)が1分で6°の速さで進んでいるような感じです。
次に短針の進む速さについてみてみましょう。
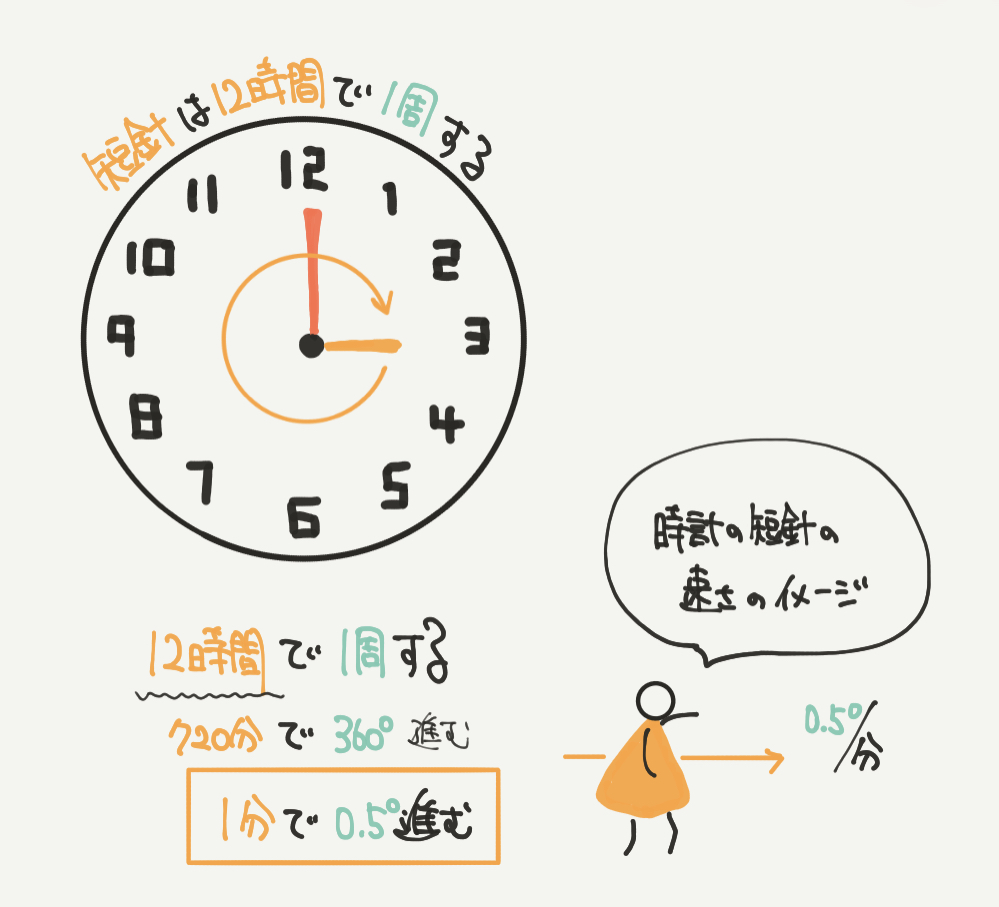
時計の短針は12時間で1周しますので、1分で0.5°進むことになります。
まとめると!!
長針の進む速さは6°/分(1分で6°進む)
短針の進む速さは0.5°/分(1分で0.5°進む)となります。
時計算を旅人算みたいに考えてみよう
時計算を得意にするためのもう一つのコツは、時計算を旅人算のように考えることです。
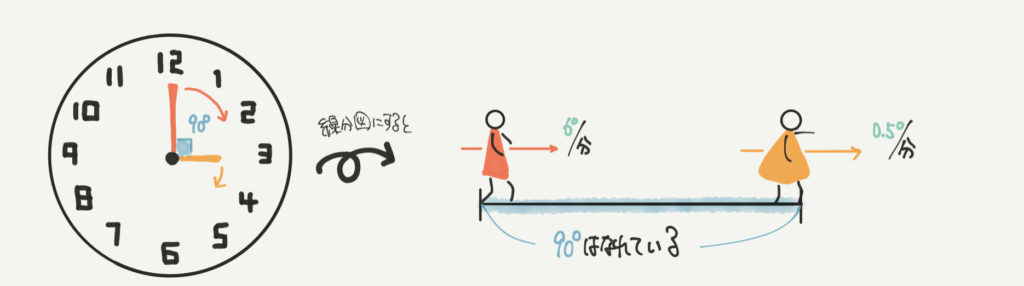
たとえば、3時のとき長針と短針の間の角度は90°になります。
そして2つの針は同じ方向に向かって進むので、線分図に変えると右の図のように書くことができます!
進む速さの単位が「m」や「km」の距離ではなく、角度(6°や0.5°)というところが
今までの旅人算と違いますがそのほかの考え方は旅人算と全く同じです!
まだよくわかっていない受験生のみなさんも今日の問題を解きながら勉強していけばOKです。
さっそく問題に挑戦していきましょう!!
問題に挑戦!
解答
答えを見るにはここをクリック!
4時21と2/11分
この記事を書いている人はこんな人


解説を読んで「 速さ 」を攻略
STEP1:まずは問題文をイメージしよう
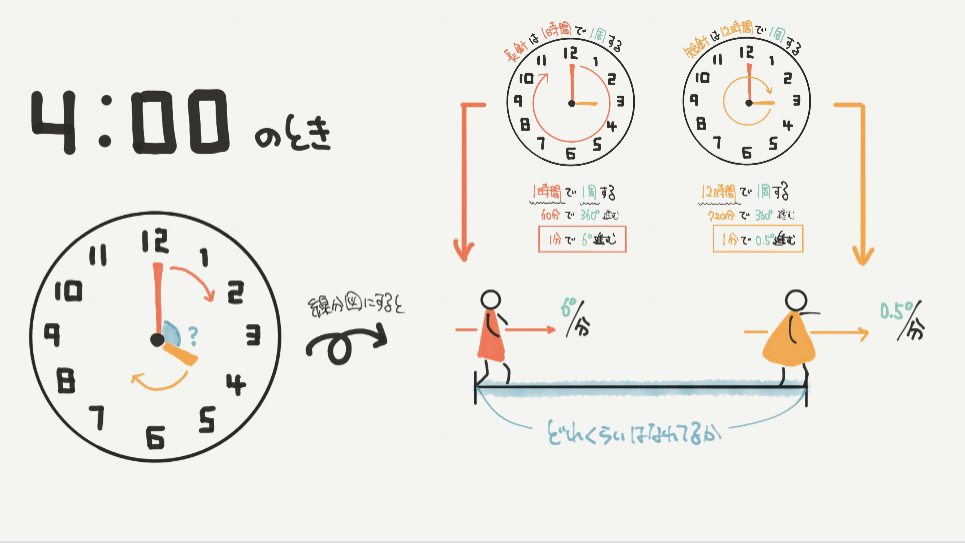
まずは問題文を図になおしていきましょう。
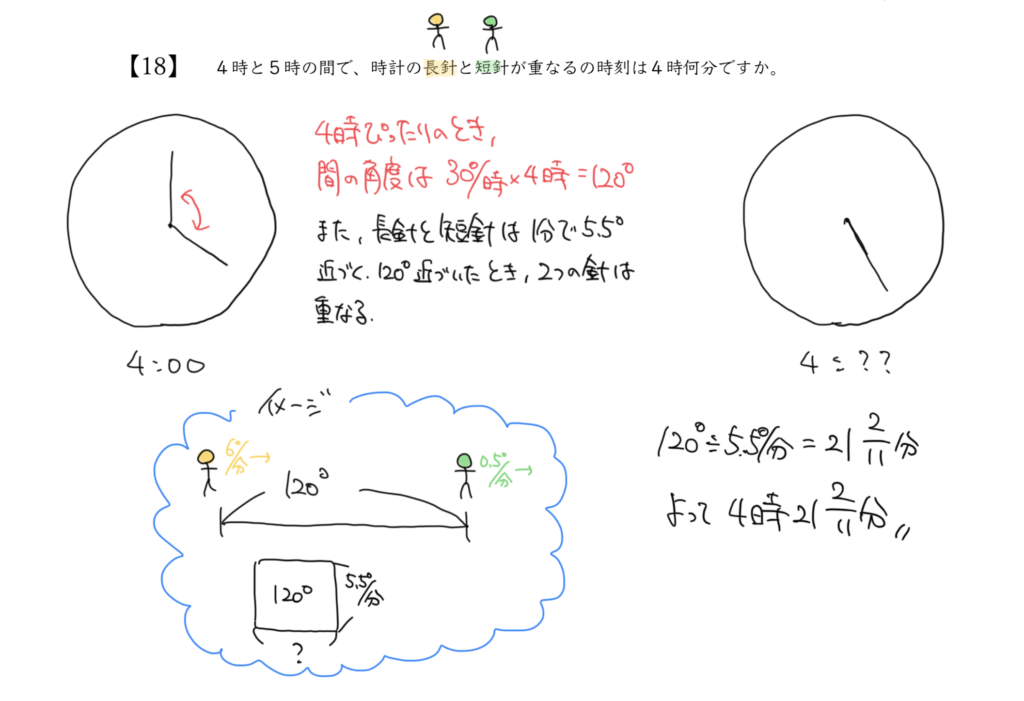
4時と5時の間で、時計の長針と短針が重なりますので、4時のときをまずは考えましょう。
長針と短針はそれぞれ同じ方向に進みますので、線分図に直すと右図のように書けると思います。
ただ、まだこのときは青い角度が何度かわかっていません。
なのでSTEP2でその角度を求めていきましょう。
STEP2:4時のとき、長針と短針はどれくらい離れている?
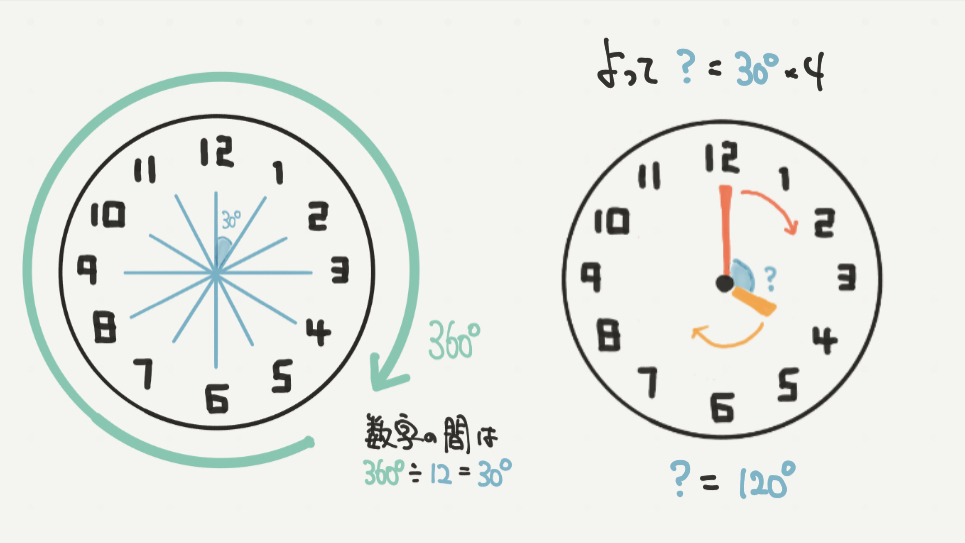
時計は1周360°、そして数字が全部で12コありますので、数字と数字の間の角度は
360°÷12コ=30°となります。
なので、4時のとき、長針と短針は
30°×4=120°と求めることができます!
STEP3:長針と短針は1分間でどれくらい近づく?
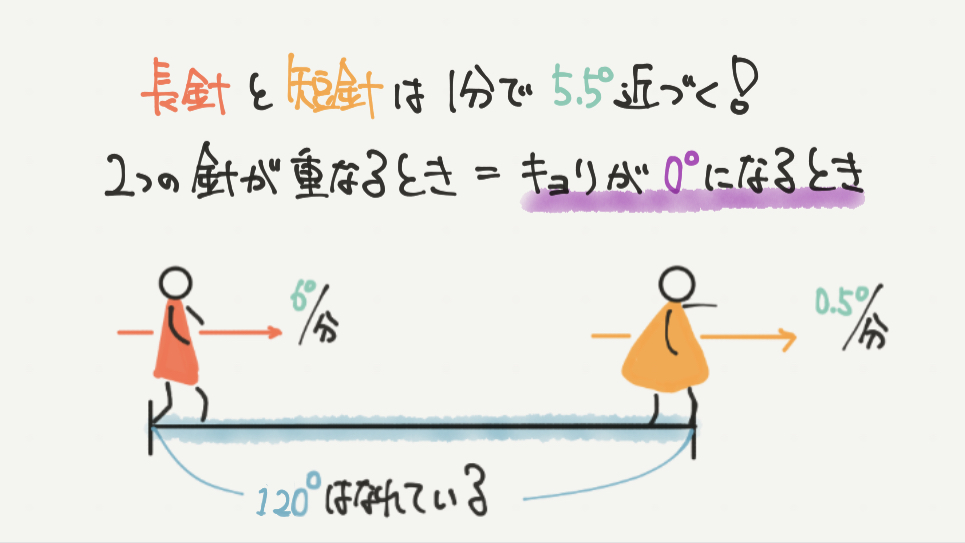
長針と短針の進む速さは最初に求めたとおり、
長針の進む速さが6°/分(1分で6°進む)
短針の進む速さが0.5°/分(1分で0.5°進む)でしたね。
なのでこの2つの針は1分間で、
6°–0.5°=5.5°進むことがわかります。
そしてこの2つの針が重なるとき、2つの針の間の角度は0°になります。
STEP4:長針と短針が重なる=2つの針の間の角度が0°のとき

時計の長針と短針が重なるということは、STEP3の赤い小人と黄色い小人が出会うことと同じです。
なのでSTEP3では長針と短針がどれくらい離れているのかを確認しました。
4時のとき、この長針と短針は120°離れていることがわかりましたので、
針が重なる時間(2人の小人が出会う時間)は
120°÷5.5°/分=21と2/11分で答えを出しましょう。
また分数は帯分数で答えましょう。
(そうすることで大体の時間がわかるのでケアレスミスを見つけやすいからです。)
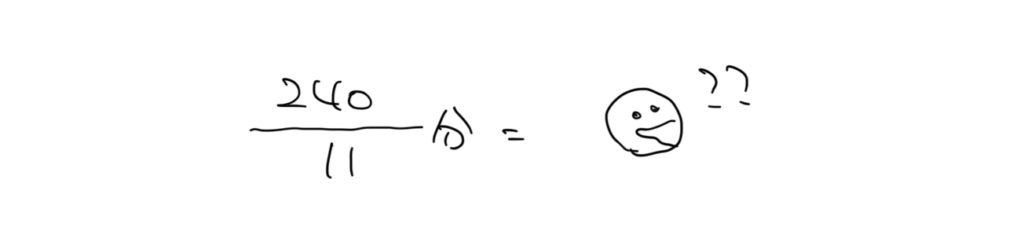
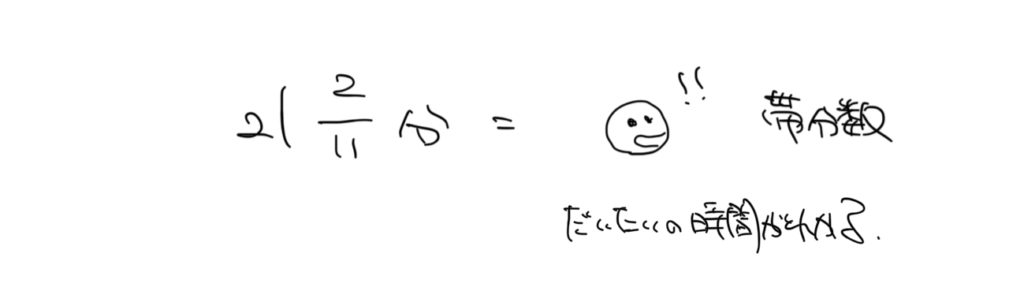
時計の長針と短針が重なる時間を求める問題のまとめ
今回の問題で大事なポイント
時計の長針と短針の進む速さ(STEP1)
時計算と旅人算の考え方(STEP2)
旅人算に関する考え方(STEP3)
以上が時計算の長針と短針が重なるときの基本問題でした。
おつかれさまでした!!
時計算の問題でよく出るタイプのものでしたが、きちんと理解できましたか?
もしわからないところがあれば下のコメントからいつでも質問してくださいね!!
前にも説明しましたが、受験で時計算が出ることはあまりありません。
ただし、その分受験で出てきたときにきちんと正解できるかが大きな合格ポイントになります。
しっかり復習して、一緒に次の問題にも挑戦していきましょう!