はじめに
今日は中学受験算数の「時計算」について勉強していきましょう!!
「さんすうがく」の基礎編で時計算を勉強するのはこれで3回目になります!
1回目、2回目については次のページの最後に紹介していますので、
今回の問題が少しむずかしいな〜と感じた受験生はまずはこの2つの問題からチャレンジしてみてください!
それではいきましょう〜
時計算の総まとめ!
今までの時計算のポイントをまとめてみます。
ここの内容がまだよくわからない受験生は、次のページの時計算の復習からやってみましょう。
時計の長針と短針の進む速さはなんだっけ?

長針の進む速さは6°/分(1分で6°進む)
短針の進む速さは0.5°/分(1分で0.5°進む)でしたね!
時計算を線分図にしてイメージしてみよう
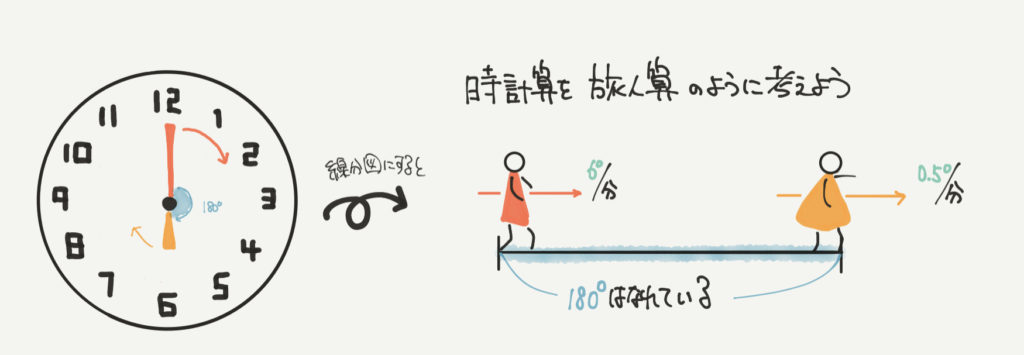
長針と短針のイメージは線分図のようになります!
今回は6時のときの図を書いているので、180°離れたところから同じ方向に進んでいると考えることができますね!
さて、この記事の問題は上の2つのポイントをきちんと理解していないと解けないくらいむずかしめな問題になっています。
分からなくても、解説でていねいに説明していますのでぜひチャレンジしていきましょう。
問題に挑戦!
解答
答えを見るにはここをクリック!
10時38と2/11分
この記事を書いている人はこんな人


解説を読んで「 速さ 」を攻略
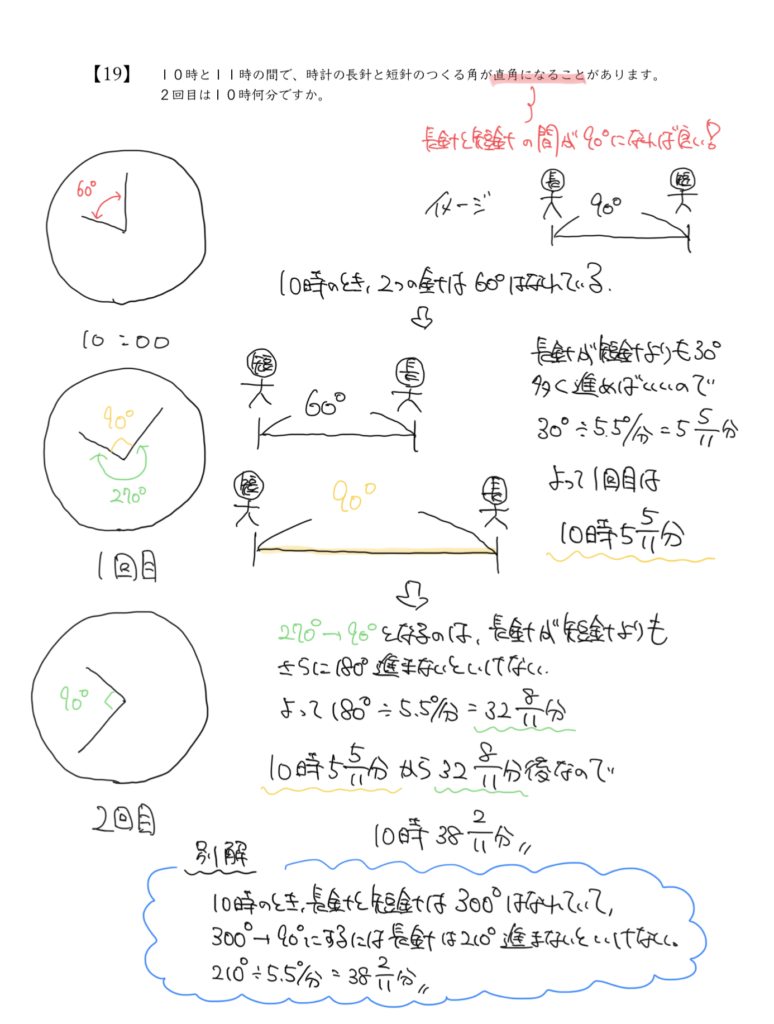
STEP1:10時のとき長針と短針がどれくらい離れているか確認しよう

さあ!まずは問題文を図にして10時のときの2つの針の間の角度を求めましょう。
このとき、数字と数字の間の角度は30°ですので、
長針と短針の小さい方の角度は60°
長針と短針の大きな方の角度は300°となります。
なので、10時のとき長針と短針は300°離れていることになります。
短針の進む速さの方が遅いので、長針と短針の間の距離は60°ではなく、300°離れていると考えよう!
STEP2:1回目、2回目に直角になるときはどういうとき?
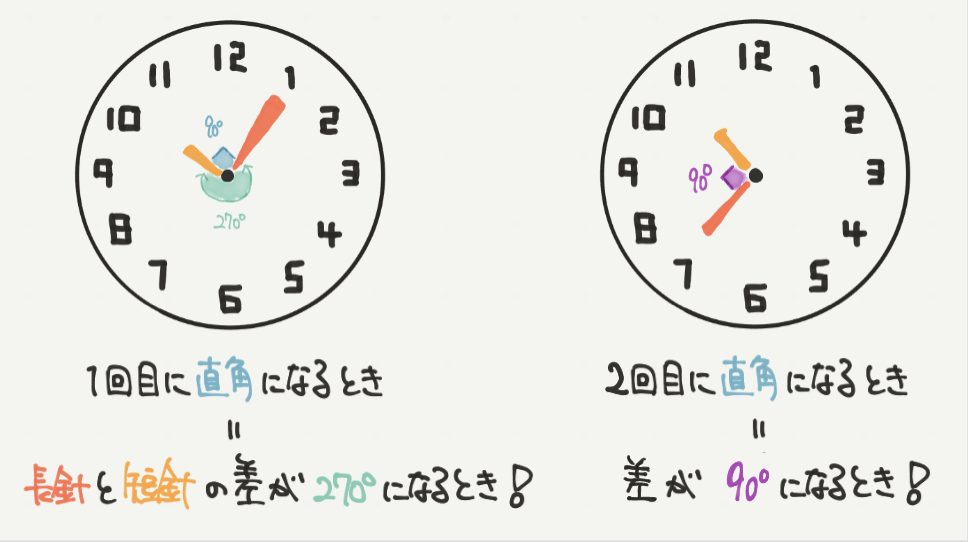
次に長針と短針が直角、90°になるときを考えてみましょう。
1回目は左の図のようなときで、長針と短針の差が270°になりますね。
また2回目は右の図のようなときで、長針と短針の差が90°になります。
このようにまずは絵をかいてイメージすることが算数を得意にするコツです!
STEP3:直角になる時を線分図にしてみよう
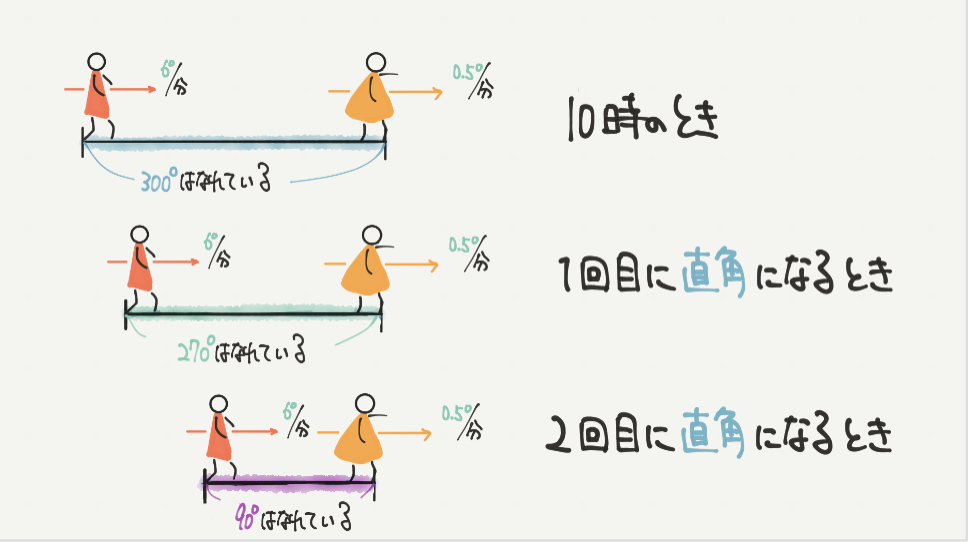
STEP2の内容を線分図になおしていきましょう。
1回目に2つの針が直角になるとき、長針と短針の差が270°になりましたので真ん中の線分図のようにかけます。
また2回目に直角になるときは、長針と短針の差が90°になるはずなので一番下の線分図のようにかけると思います。
ここまでついて来れていますでしょうか?
もう少しです!がんばりましょう。
STEP4:長針は短針よりも210°多く進めば2回目に直角になる!
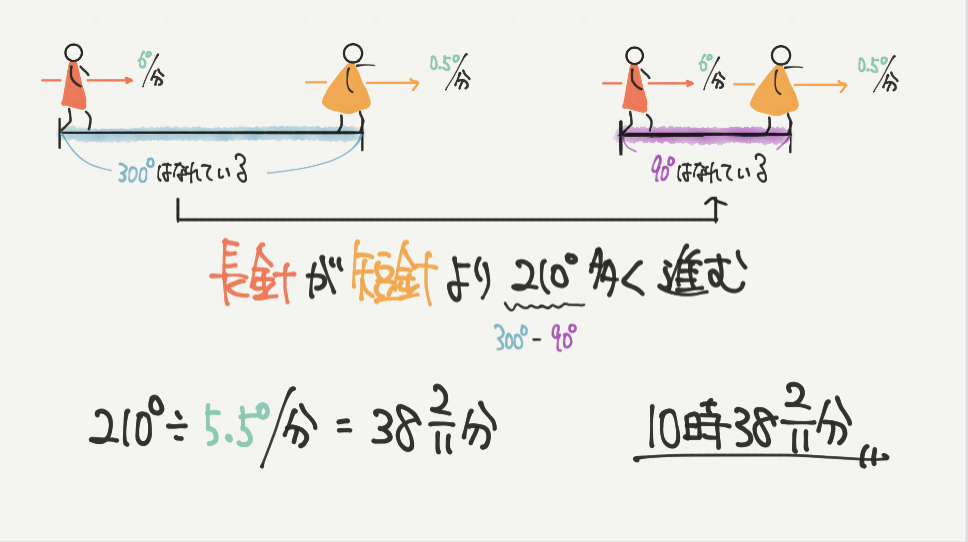
STEP3より、10時のときから2回目に長針と短針が直角になるまでに
長針が短針よりも210°多く進めばいいことがわかりました。
そして長針の進む速さは6°/分で短針の進む速さは0.5°/分なので、
2つの針の1分間で近づく距離は5.5°/分となります。
よって答えは、210°÷5.5°/分=38と2/11分で、
10時38と2/11分と求めることができました。
時計の長針と短針が直角になる時間を求める問題のまとめ
今回の問題で大事なポイント
時計の長針と短針の進む速さ(はじめに)
時計算と旅人算の考え方(はじめに)
・線分図をきちんと書くこと(STEP3)
直角になるときはどういうときか?(STEP2)
今回の問題もほかの時計算の問題と同じで、長針が短針の進む速さや旅人算のように線分図を書いてみることが大切でした。
どんなにむずかしそうな問題でも、まずはお絵かきしてみるといいと思います。
頭の中だけで計算してしまうとミスしてしまいますので、復習はていねいにするようにしましょう〜!!
時計算の少しかんたんな問題の復習
時計の長針と短針の作る角度を求めるには?

時計の長針と短針が重なる時間を求めるには?