はじめに
みなさんこんばんは!!
今日のテーマは中学受験算数の「平面図形」についてです!
今日の問題は平面図形でよくでる角度に関する問題です。
問題を解くまえに図形の基本についてかんたんに説明していますので見ていきましょう。
苦手な人も多い平面図形ですが、安心してください!まずは一緒にヒントから勉強しましょう
4つの図形について確認しよう
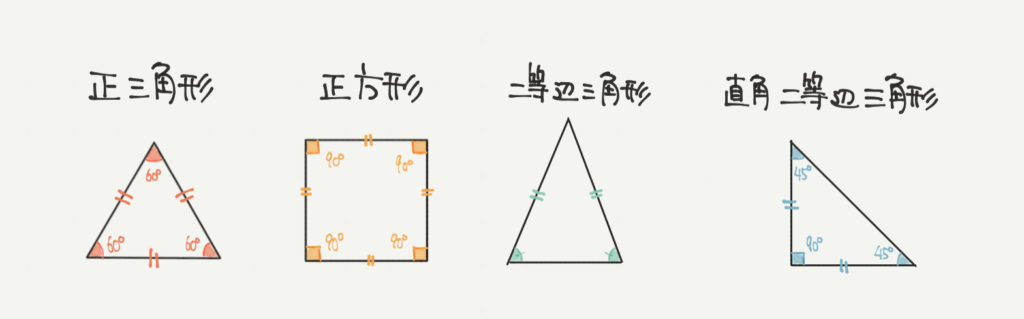
正三角形の基本
- 正三角形は全ての辺の長さが同じ
- 1つの内角の角度は60°
- 三角形の内角の和が180°なので180°÷3=60°
正方形の基本
- 正方形は全ての辺の長さが同じ
- 1つの内角の角度は90°(直角)
- 四角形の内角の和が360°なので360°÷4=90°
二等辺三角形の基本
- 二等辺三角形は2つの辺の長さが同じ
- 2つの内角が等しくなる
- 同じになる内角は、辺に対応している
- 内角の角度は問題によって変わってくる
直角二等辺三角形の基本
- 直角二等辺三角形は2つの辺の長さが同じ
- 角度は90°、45°、45°となる
 わかみや先生
わかみや先生ここまでは理解できましたか?
今日の問題ではこれらの図形の基本を使います!
それではさっそく問題にチャレンジしていきましょう!
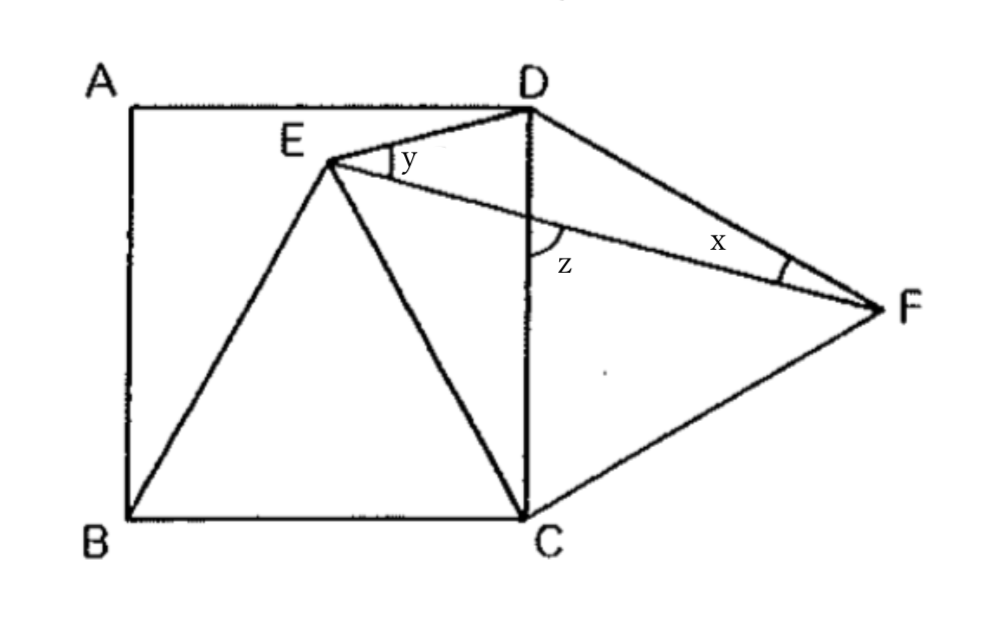
問題に挑戦!

解答
答えを見るにはここをクリック!
x°=15度(15°)
y°=30度(30°)
z°=75度(75°)
この記事を書いている人はこんな人



解説を見てみよう!

STEP1:問題文からわかることを書いていこう
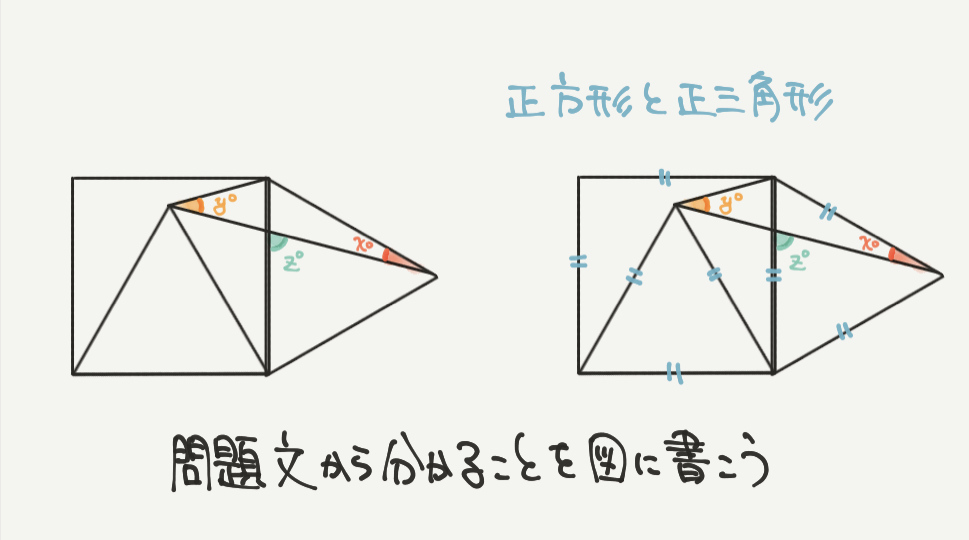

平面図形の問題では、わかる情報を図に書きこむことが大切になってきます。
今回の問題では正方形と正三角形の長さが同じですので右のように図に書くことができます。
辺の長さが同じなので、きちんと全部の辺の長さが同じであると書いておきます。
ここから3つの角度を求めていきましょう。
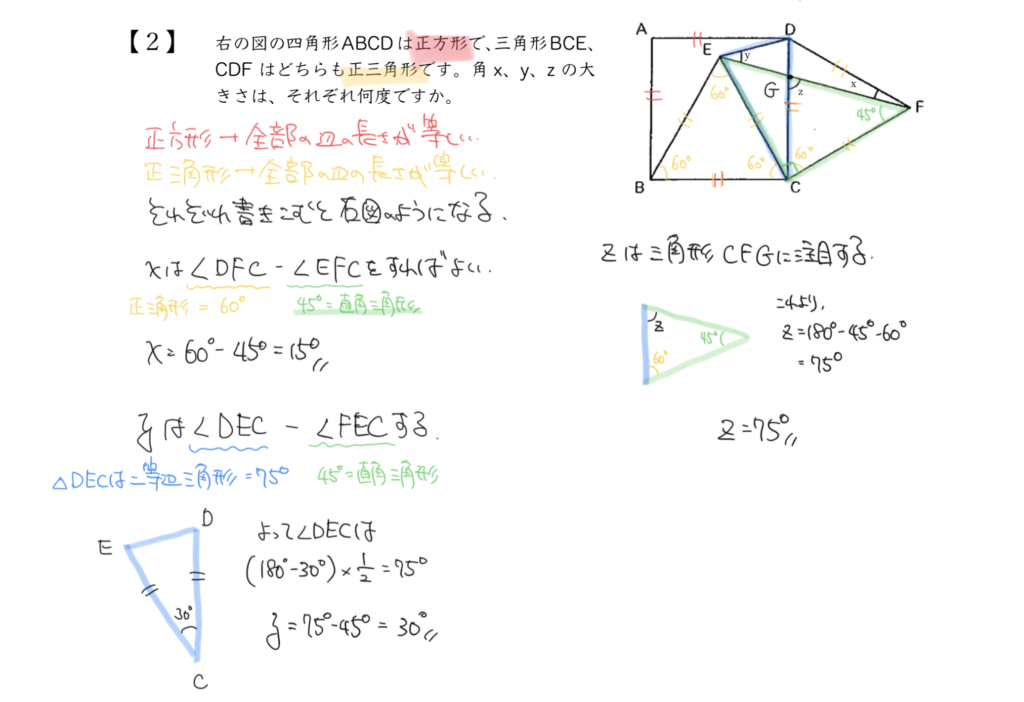
STEP2:x°の角度を求めよう
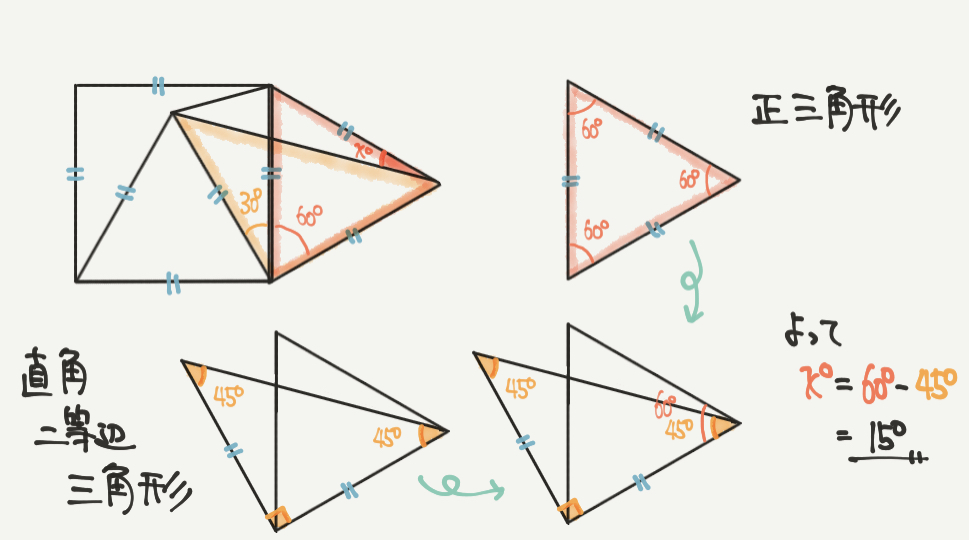

まずはx°の角度を求めましょう。
ここで注目するのは直角二等辺三角形と正三角形です。
はじめにで勉強したとおり、直角二等辺三角形の角度は90°、45°、45°で、
正三角形の角度は60°になります。
x°はこの2つの角度の差なので、
60°–45°=15°となります!
STEP3:y°の角度を求めよう
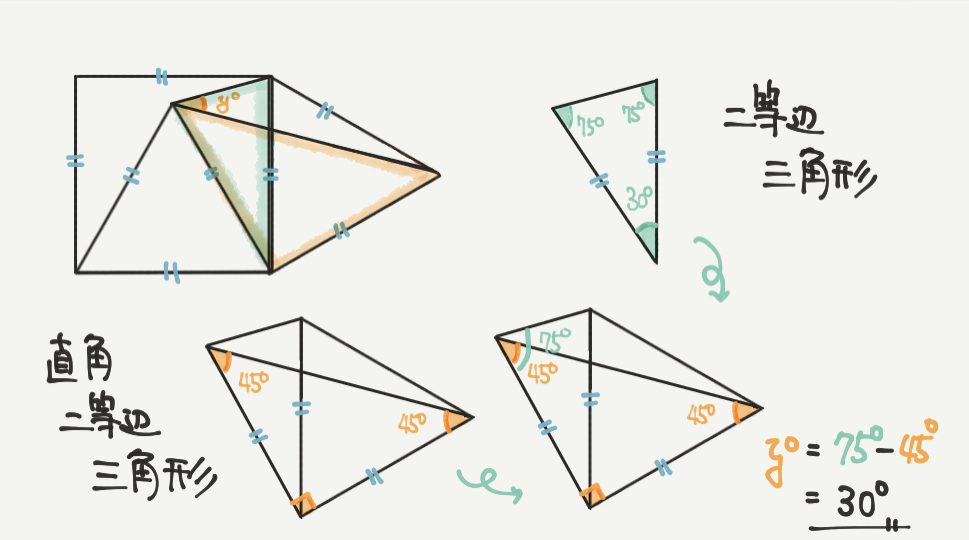
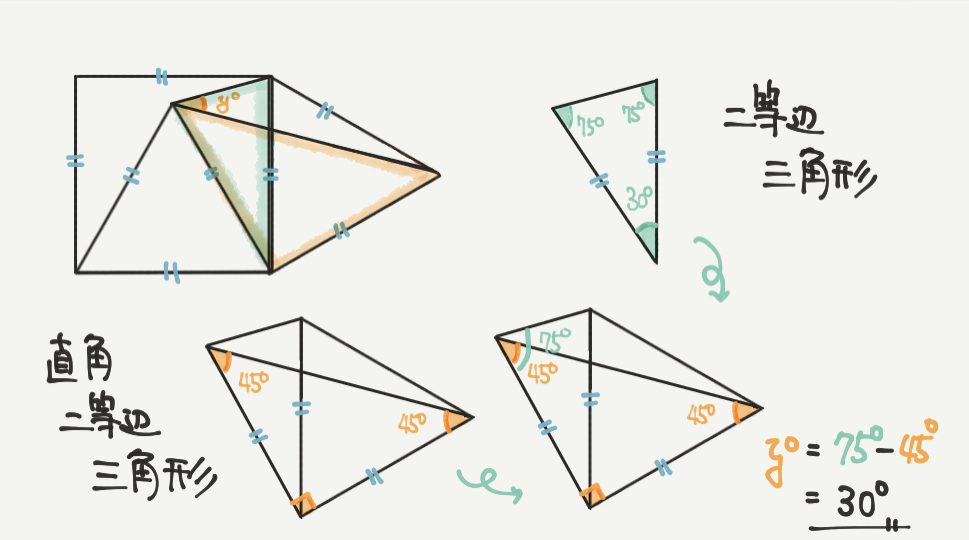
次にy°の角度を見ていきましょう。
ここで注目するのは直角二等辺三角形と二等辺三角形です。
こちらもSTEP1と同じように、直角二等辺三角形の角度は90°、45°、45°になります。
二等辺三角形の角度は30°の部分が先にわかります。
↑正方形の90°-正三角形の60°=30°
よって二等辺三角形の角度は30°、75°、75°と求まります。



二等辺三角形の2つの角度が同じなので、
180°-30°=150°(残り2つの角度の和)
150°÷2=75°ということだね!!
y°は75°と45°の差なので、
75°–45°=30°
と計算することができました。
STEP4:z°の角度を求めよう
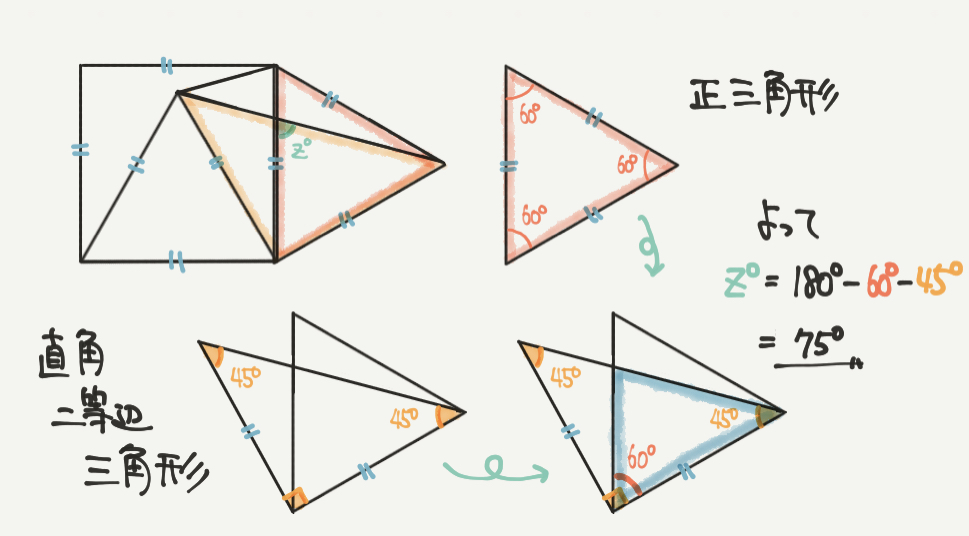

最後にz°の角度を求めましょう。
ここで注目するのはSTEP1と同じ、直角二等辺三角形と正三角形です。
直角二等辺三角形の角度はさっきと同じで90°、45°、45°で、
正三角形の角度は60°になります。
z°はこの2つの図形が重なった三角形を見れば求めることができます。
180°-60°–45°=75°
となります!
重なった正方形と正三角形から角度を求める問題のまとめ
今回の問題で大事なポイント
4つの図形の基本(はじめに)
問題文の内容を図に書きこもう!(STEP1)
以上で今日の問題はおしまいです。
おつかれさまでした〜!!
受験生だったときの私は、他の問題と比べて平面図形の問題は好きでした。
なぜなら平面図形の問題はすでに図が問題に書いてあるからです。
まずはその図にすべての情報を書きこむことが大切でした。
今回の問題なら、正方形、正三角形と書いてあるのですぐに書きこみましょう。
わかることを全部図に書くのは「和と差に関する問題」や「割合と比の問題」でも同じです!
「さんすうがく」の問題全部に言える大事なポイントですね。
あとは解説通りに解いていけば答えにたどり着けるはずです。
まだまだ平面図形の問題は続いていきますよ!がんばっていきましょう。