はじめに
みなさんこんにちは!!
今日のテーマは中学受験算数の「平面図形」についてです!
今回は図形に加えて新しい考え方「等積変形」について勉強していきましょう。
「等積変形」という言葉は聞いたことあっても何なのか
よく分かっていない受験生も多いと思いますが、大丈夫です!
今から一緒に勉強していけばきちんと理解することができますよ。
等積変形ってなに?

等積変形とは、同じ面積になるように図形を変形するやり方のことです。
なんでこんなことをやるのか?というと問題をかんたんに解くことができるからです。
等積変形の見つけ方
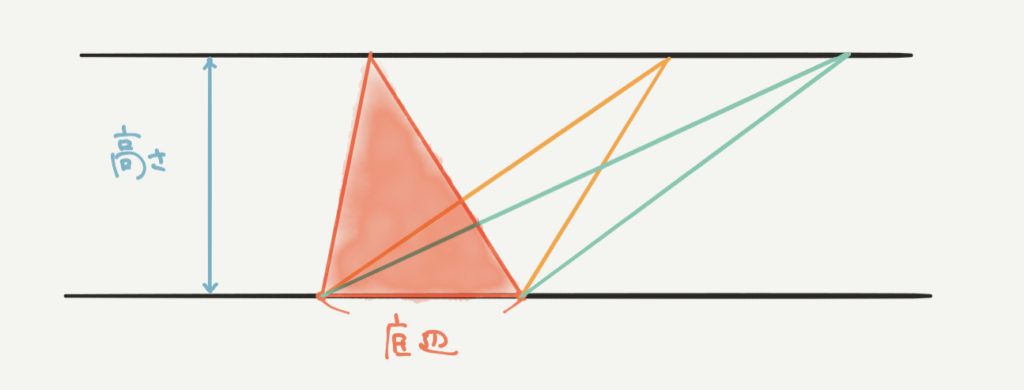
では、どのように等積変形を見つけたらよいのでしょうか?
まずは、こちらの三角形を見てみてください。
赤い三角形の面積は、底辺×高さ×1/2で求めることができますね。
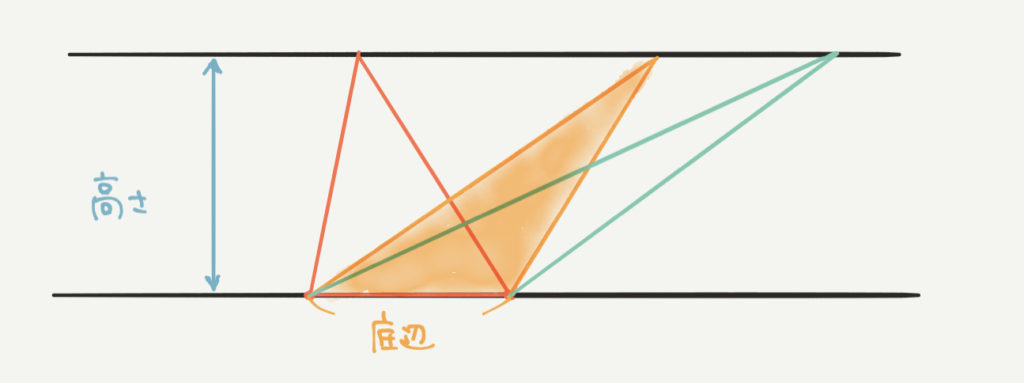
同じように考えると黄色の三角形の面積も、底辺×高さ×1/2で求めることができます。
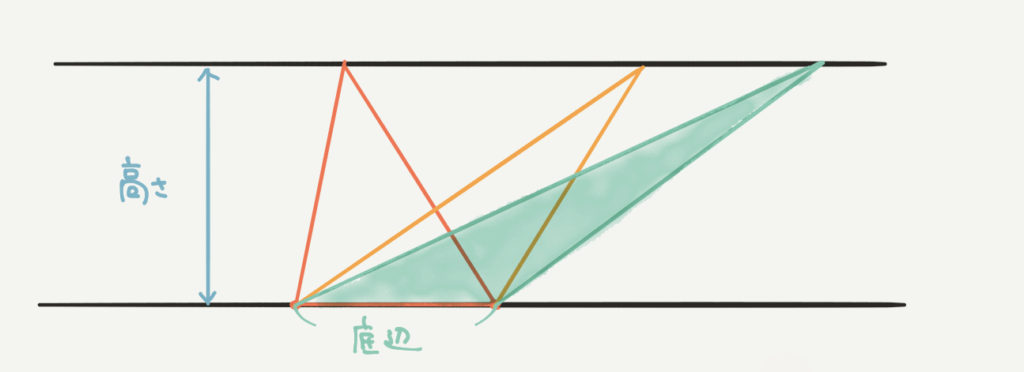
最後に緑の三角形です。
この三角形も底辺×高さ×1/2で面積がわかりますので、
赤:底辺×高さ×1/2
黄:底辺×高さ×1/2
緑:底辺×高さ×1/2
↑底辺の長さはどれも同じ!
よって赤と黄と緑の3つの三角形の面積が同じであると分かります。
この同じ面積を見つける考え方が「等積変形」において大切になってきます!
ぜひ問題を解きながら考えていきましょう。
問題に挑戦!
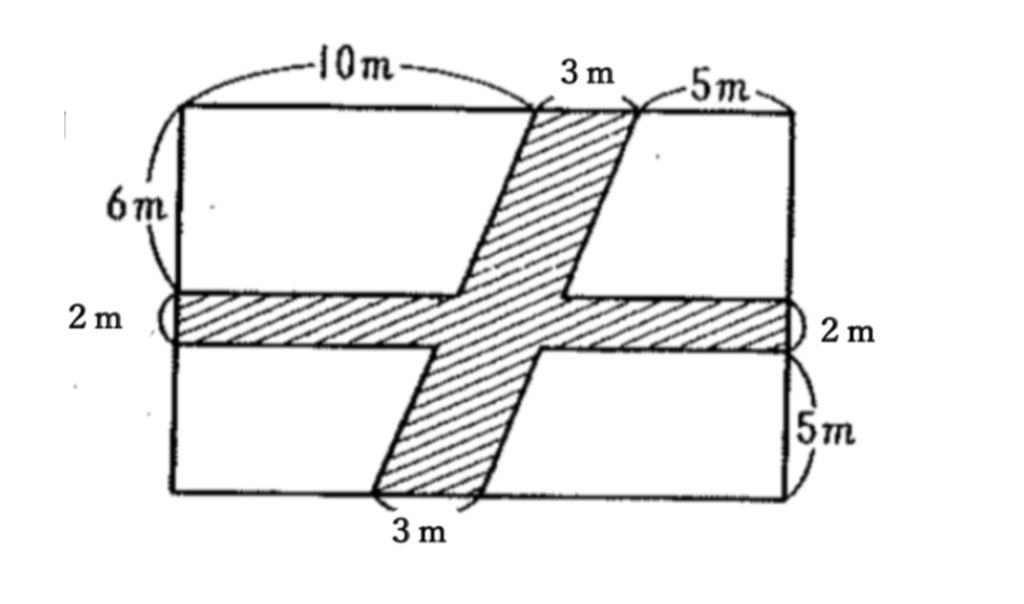
解答
答えを見るにはここをクリック!
165㎡
この記事を書いている人はこんな人


解説を見てみよう!
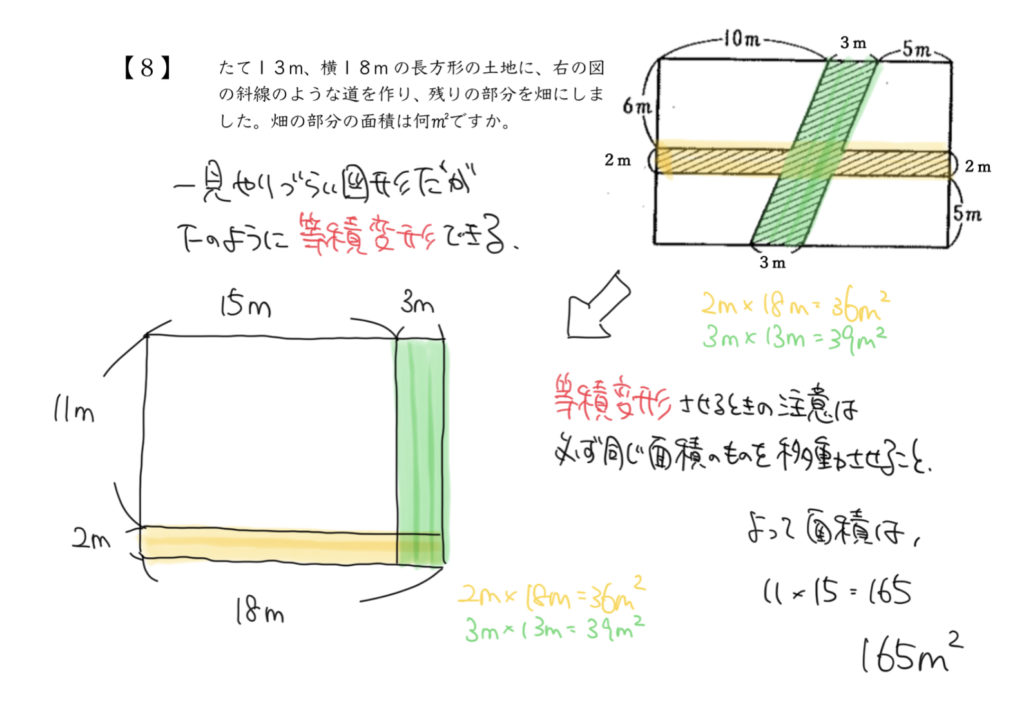
STEP1:四角形の面積の求め方を復習しよう
まずは問題を解く前に四角形の面積の求め方をおさらいしておきましょう。
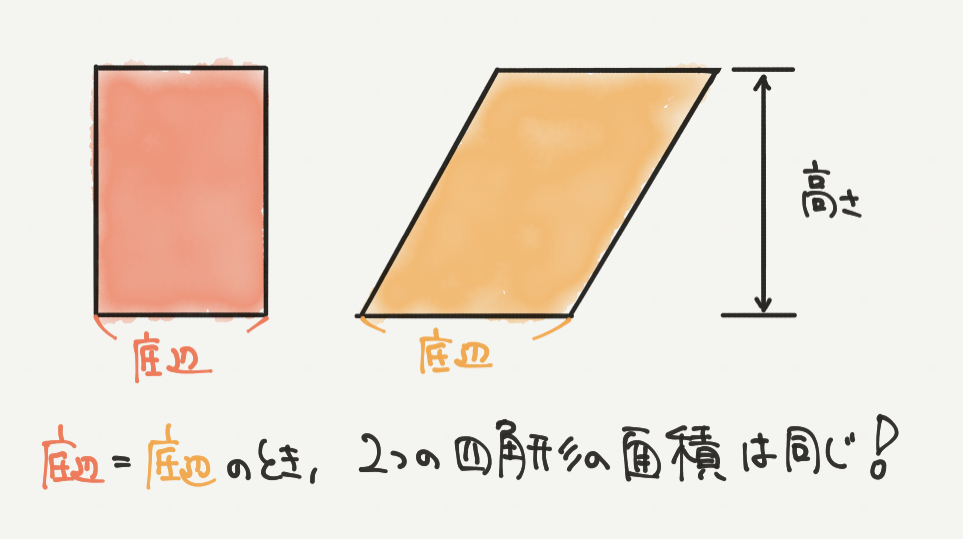
赤い四角形も黄色い四角形も底辺の長さが同じとき、(底辺=底辺)
2つの四角形の面積は、
赤:底辺×高さ
黄:底辺×高さ
なので2つとも同じになります!
今回はこの四角形の考え方を使って問題を解いていきましょう。
STEP2:同じところを見つけよう
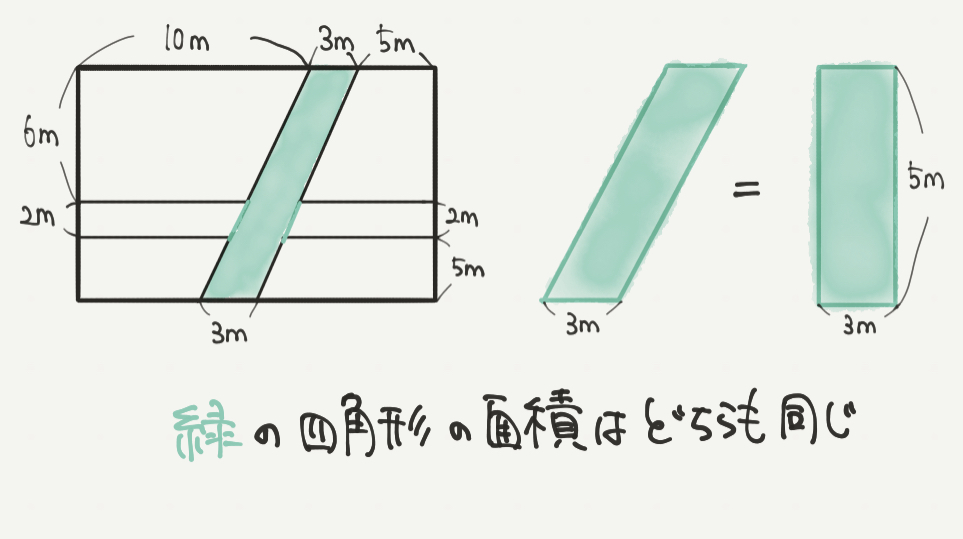
STEP2では問題文の図からさっきの四角形を探してみましょう。
すると緑の平行四辺形がSTEP1の黄色い四角形と同じ形だとわかるはずです。
この平行四辺形も普通の四角形も面積の求め方は「底辺×高さ」なので、
右の図のように緑の平行四辺形を長方形に変形できます!
この変形を使って問題を解いていきますよ!
STEP3:問題文の図形を等積変形しよう
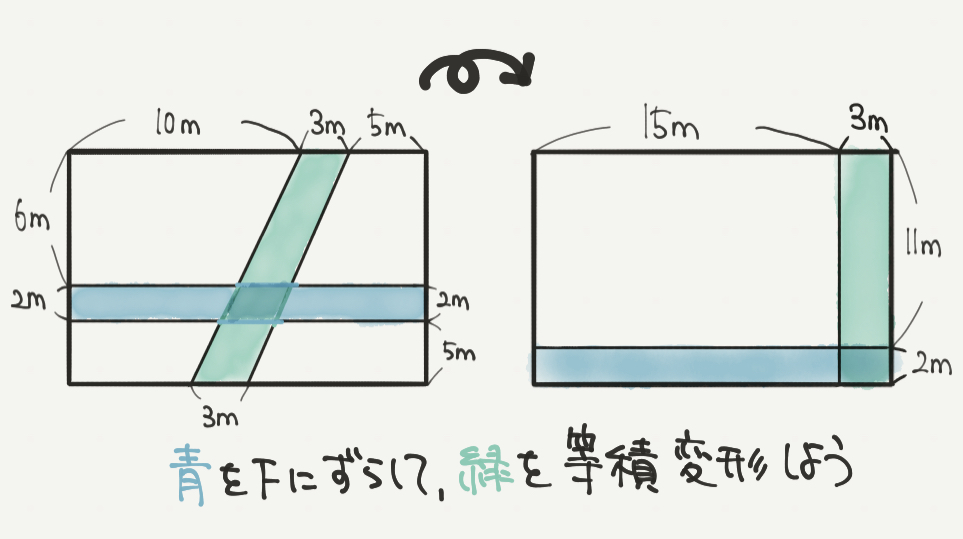
STEP2で緑の四角形を変形することができたので、緑の四角形を右のはじっこに移動させちゃいましょう。
図形を移動させるときは、ちゃんと面積を確認しましょうね。
今回は底辺が3mの四角形を移動させているので、
移動させた後の四角形の面積も底辺は3mになるはずです。
そしてもう一つの青い四角形も真ん中から下にずらしてはじっこによせてしまいましょう!
すると、複雑な図形がスッキリしてきたと思います。
STEP4:答えを計算して求めよう
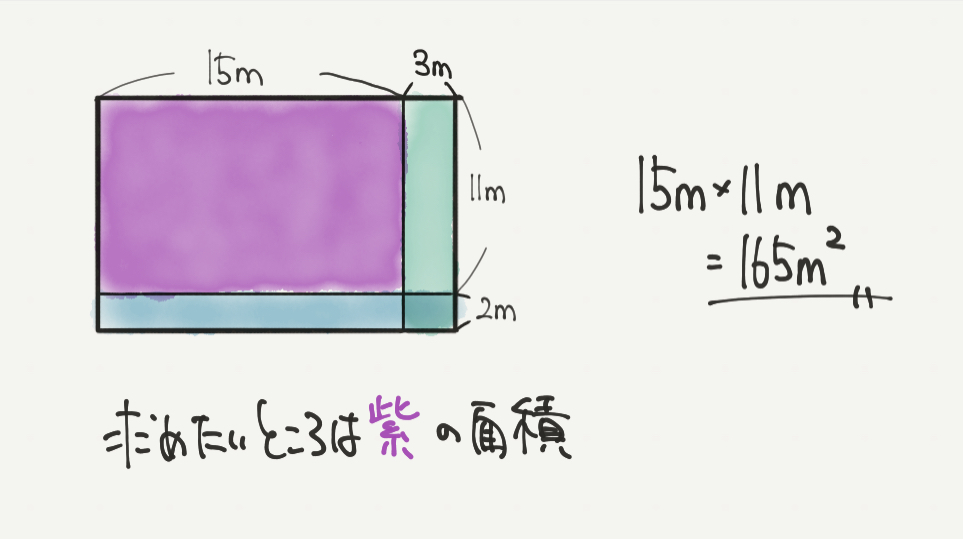
さあ、ここまで来たらあとは計算するだけです!
求めたい答えの部分は緑でも青でもなく紫の部分なので、
四角形の長さをきちんと理解していれば解くことができますね!
15m×11m=165㎡
が答えになります。
 わかみや先生
わかみや先生図形を「等積変形」させたとき、
長さについてもきちんと書いておくようにしましょう!
長方形の中の複雑な斜線の部分の面積を求める問題のまとめ
今回の問題で大事なポイント
- 等積変形の基本(はじめに)
・同じところを見つけよう(今回は四角形の面積が同じなので、それを使って移動させましたね)
・正しく図形を移動させよう!(長さを適当に考えたらダメ!)
「等積変形」の問題はこちらでおしまいです!!
みなさんきちんと正解できましたか?
今回の問題は「等積変形」の初歩的な問題になりました。
慣れてくればかんたんに解けると思いますが、はじめはむずかしいと思います。
なので最初は間違ってしまっても大丈夫です!
今回注目した「等積変形」のポイントは「四角形の面積=たて×横」ということでしたね。



ほかの問題でも「等積変形」のポイントは必ずありますので、
どこが同じなのか?という考えを持ちながら
平面図形の問題を解いていきましょう!