はじめに
みなさんこんにちは!!
今日のテーマは中学受験算数の「平面図形」についてです!
今回挑戦する問題も図形の角度を求めるような問題です。
まずは問題で出てくる三角定規や角度をぱぱっと求めることができるコツについて解説していきます。
平面図形の問題って、時間をかければ解けるけど
テストだと時間がなくてあせって解けなくなって困る人も多いのではないでしょうか?
たしかに、平面図形の問題は時間をきちんとかけて解けば解ける問題が多いですよね。
でもテストでは時間が決まっているので「どれだけ早く、正確に答えを出すか」が大事になります。
ここで解説するコツをしっかりと勉強して問題を解いてみましょう!
三角定規の基本
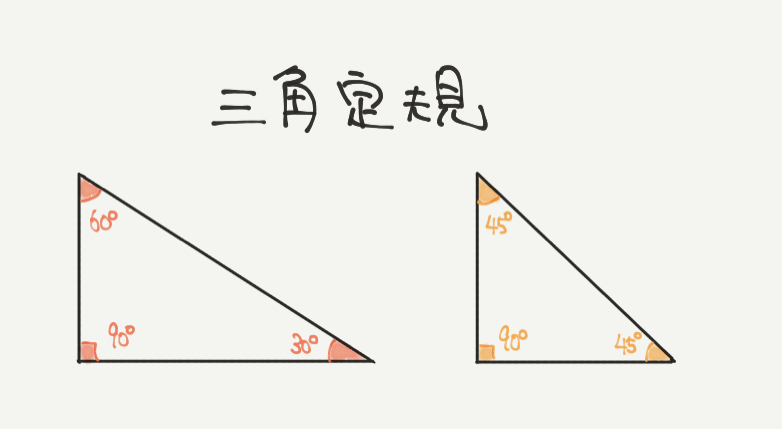
まずは小学校でもよく見かける三角定規についての基本を勉強しましょう。
三角定規は角度が決まっている2つの三角形のことです。
1つは直角三角形で、30°、60°、90°の角度になります。
もう1つは直角二等辺三角形で角度は45°、45°、90°となります。
今回の問題ではこの知識を知らないと解けないので、きちんと覚えておくようにしましょう。
スリッパの考え方を使ってかんたんに角度を求めよう
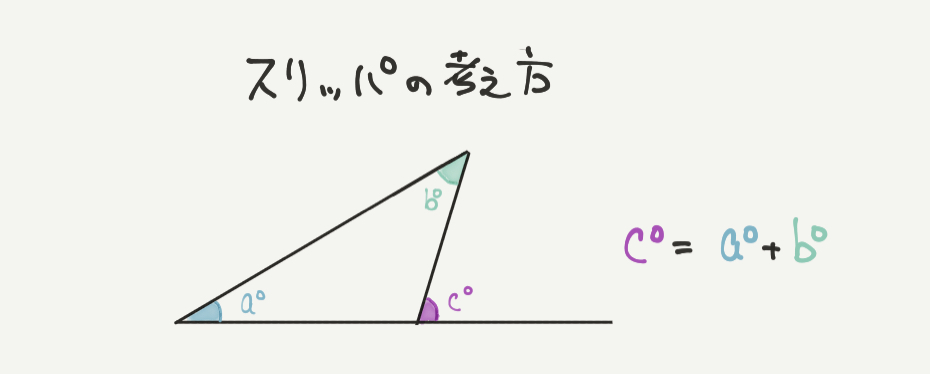
次に角度をかんたんに求めることができるスリッパの考え方について解説します。
上の図のように、スリッパの形の図形を見かけたら角度をこのように求めましょう。
c°=a°+b°
なんでc°=a°+b°になるの?
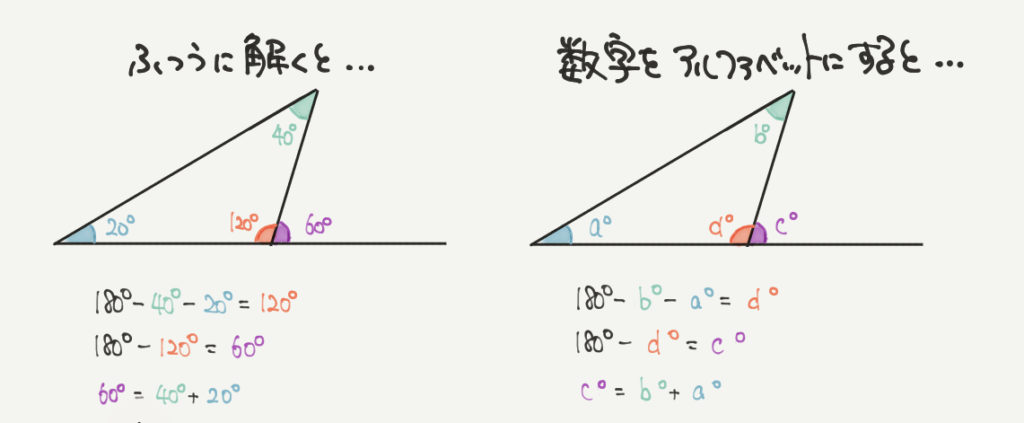
では、なぜc°=a°+b°になるのか考えてみましょう。
ここではかんたんな例で考えて、実際の数字を使っています。
a°=20°、b°=40°としてみましょう。
すると三角形の内角の和は180°なので、
赤い角度が180°–20°–40°=120°と計算できます。
よって紫の部分は180°–120°=60°となり、
60°=20°+40°となるのがわかると思います。
これをアルファベットの記号で表したのが右のグラフです!
このようにどのような角度であっても、スリッパの形をしていればc°=a°+b°が成り立ちます!
 わかみや先生
わかみや先生これを覚えておくと問題がサクッと解けるようになります!
ぜひ使ってみてください。
スリッパの応用の考え方
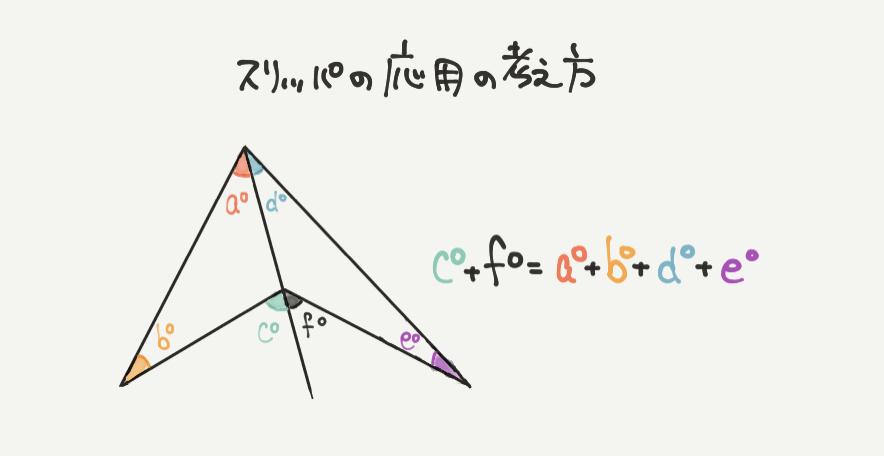

ちなみに少し応用ですが、スリッパを2つ重ねた形もあります!
↑さっきのスリッパの考え方よりも少しむずかしいので、わからなかったら飛ばしても大丈夫です!
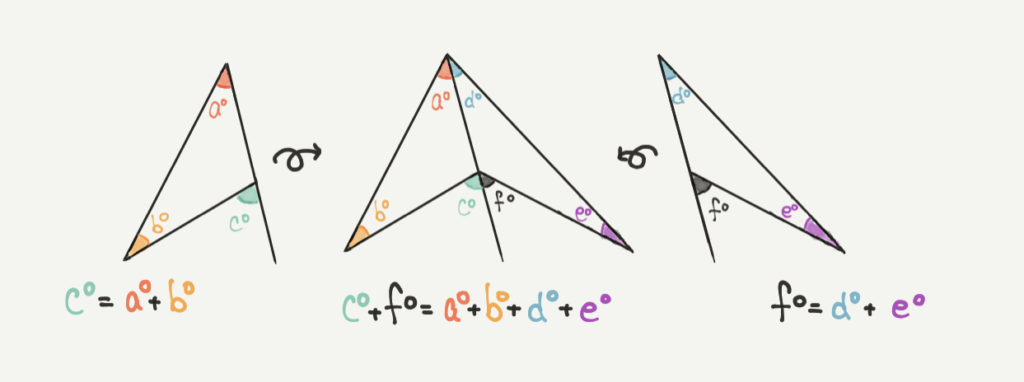
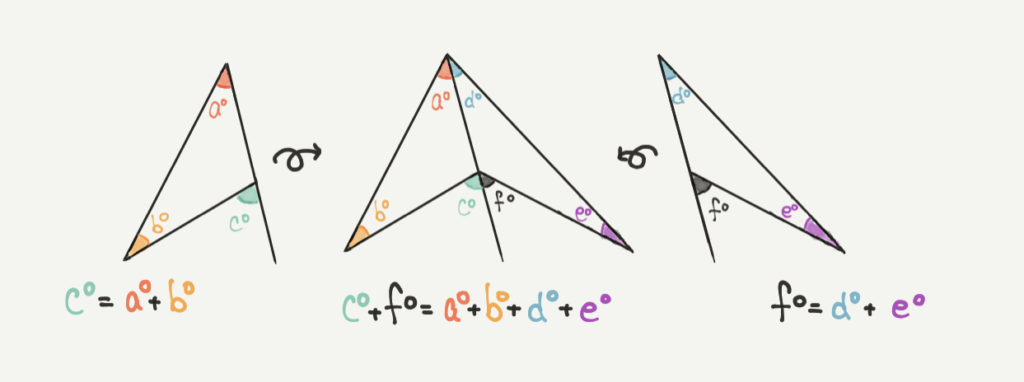
こちらの考え方は、スリッパを2つ重ねています。
c°=a°+b°が左のスリッパで、f°=d°+e°が右のスリッパになります。
この2つを組み合わせると、
真ん中の角度(c°+f°)=a°+b°+d°+e°ということが分かると思います。
これがスリッパの考え方の応用です!



このスリッパの応用の考えを知っている受験生と知らない受験生とでは、解くスピードが全然違います!覚えやすい形だと思うので、
今回の問題ではこの考え方も使って解いてみましょう!
問題に挑戦!
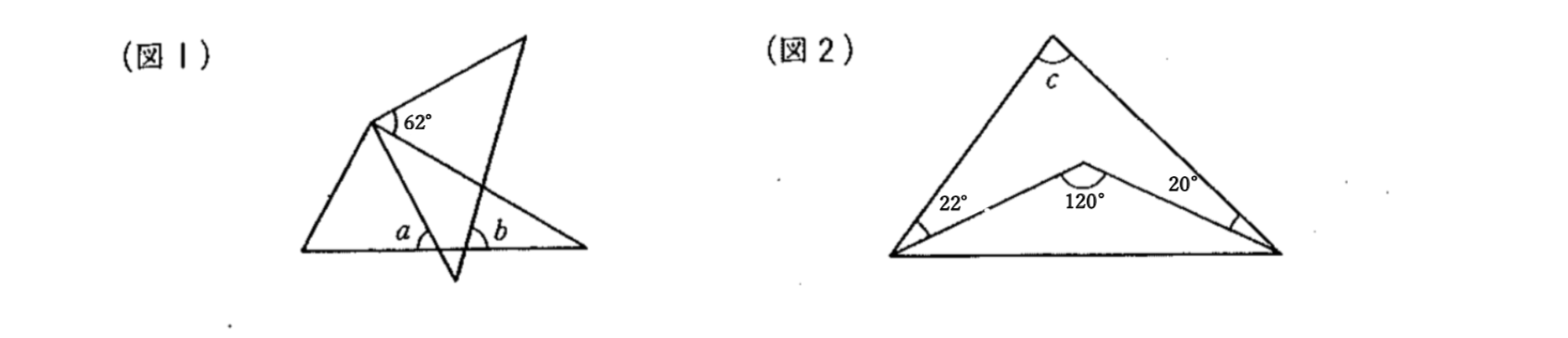

解答
答えを見るにはここをクリック!
a=58度(58°)
b=77度(77°)
c=78度(78°)
この記事を書いている人はこんな人



解説を見てみよう!
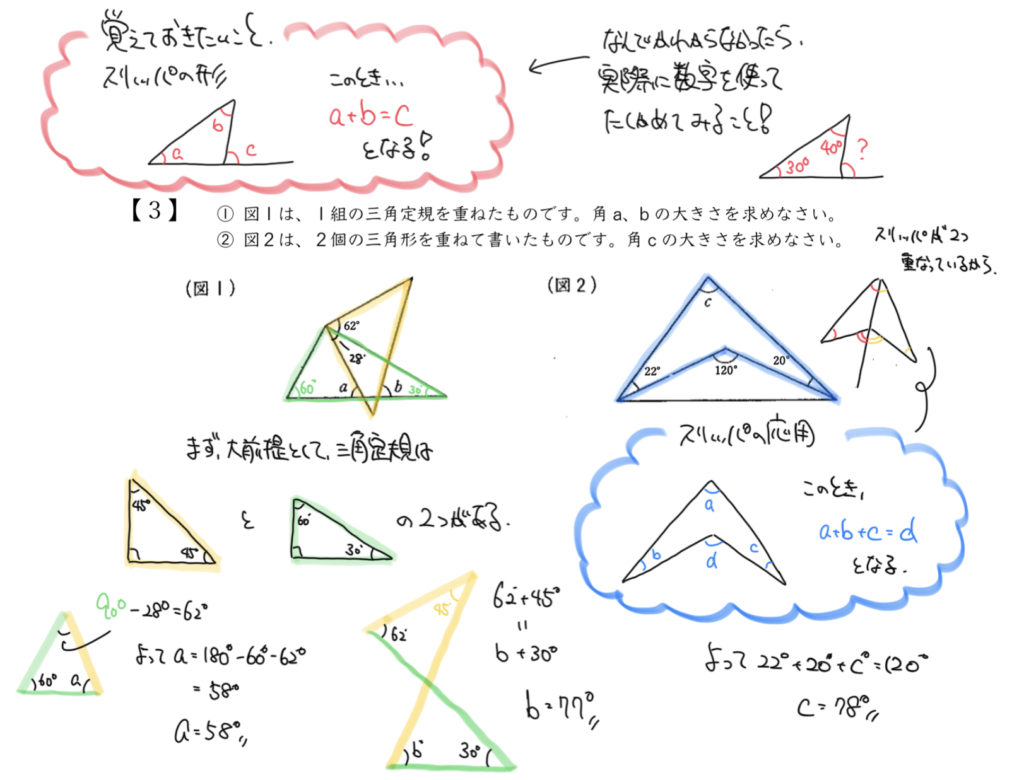

STEP1:問題の図からわかることを書きこもう
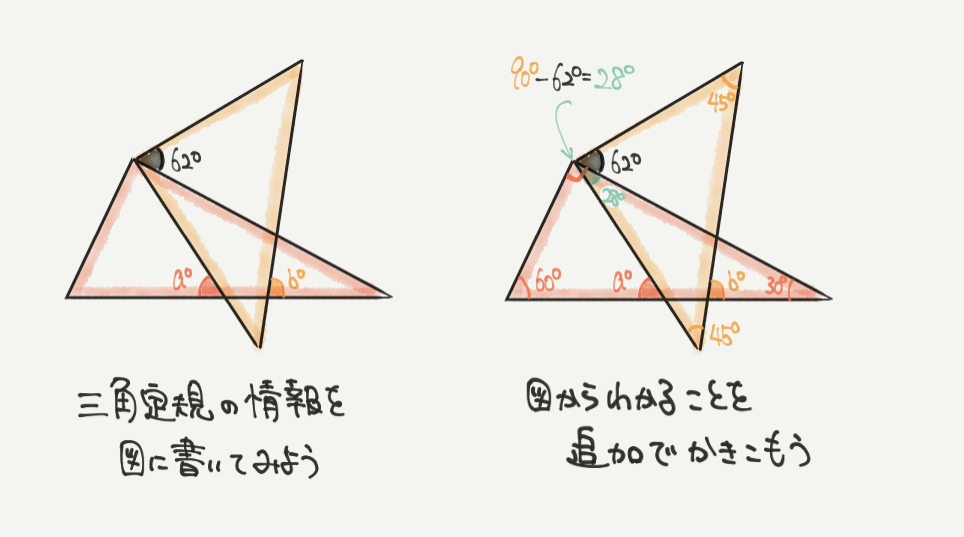

まずはaとbについて考えていきましょう。
この問題では2つの三角形は三角定規と言われているので、さっき説明した
直角三角形→30°、60°、90°
直角二等辺三角形→45°、45°、90°
の情報を問題の図に書いていきます!
ほかにも今回62°がわかっているので、緑の角度が
90°(直角)-62°=28°となりますね。
ここまできちんと書ければSTEP1は完了です!!
STEP2:aの角度を求めよう
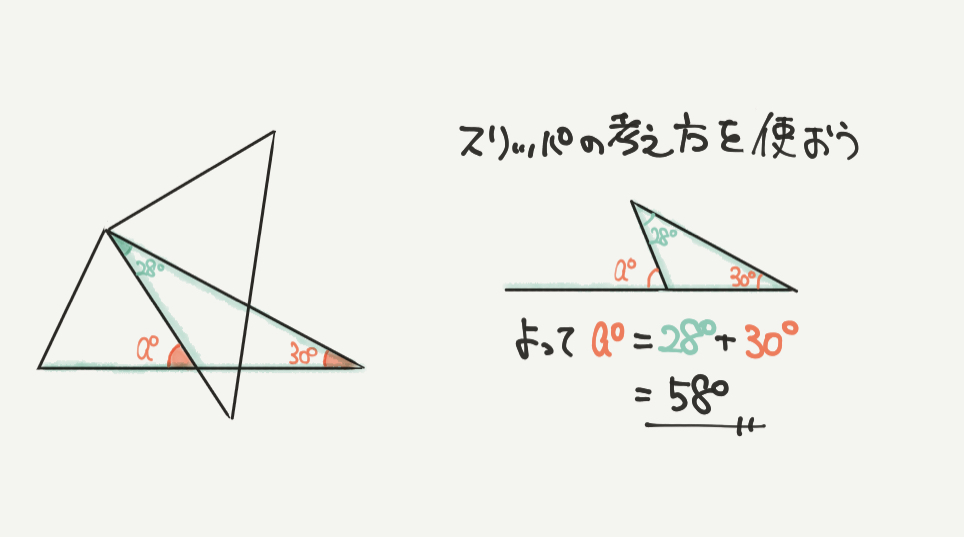
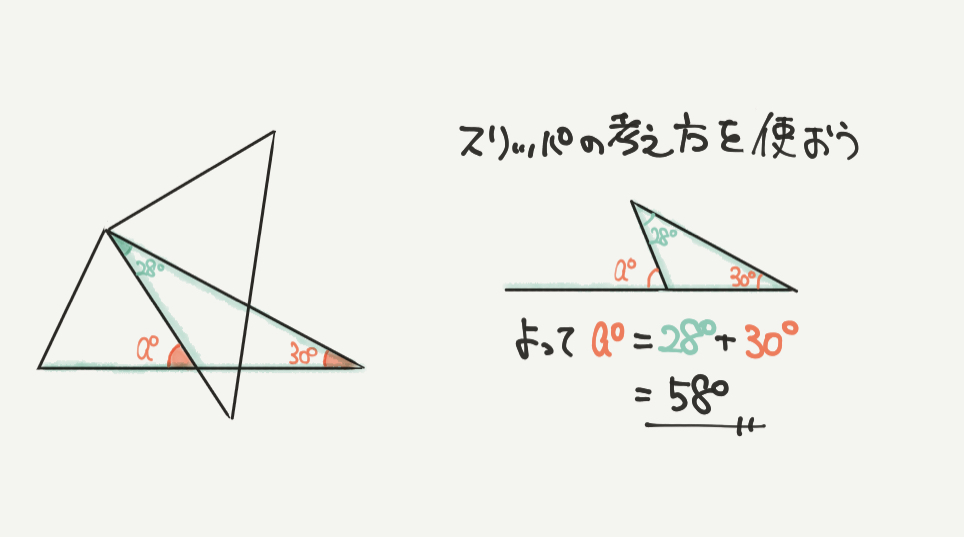
次にさっそくaの角度を求めましょう。
aの角度はとてもかんたんに求められて、緑色のスリッパを見つけることができれば一発です!
さっき勉強したスリッパをさっそく使うと、
aの角度は28°+30°=58°と計算することができます。
STEP3:bの角度を求めよう
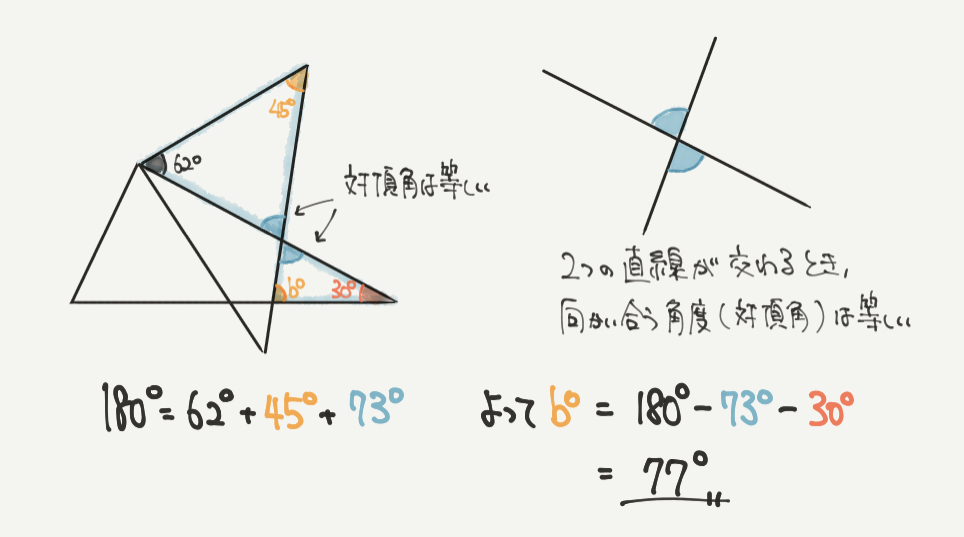

次に少しむずかしいbの角度を見ていきましょう。
bの角度を出すには青色の2つの三角形に注目していきます。
まず、上の青色の三角形を見てみると、
45°+62°+青色の角度=180°(三角形の内角の和)となります。
よって
青色の角度=180°-45°-62°で、
青色の角度=73°とわかります。
青の三角形の中にある2つの青色の角度は対頂角と言って、角度が同じになります。
なので反対側の青い角度も73°となります。
この知識を使ってbを求めていきましょう。
bの方の三角形は、
180°=b°+30°+73°なので
b°=180°–30°–73°
b°=77°と求まります。
ここまでが①の解説でした!
STEP4:cの角度を求めよう
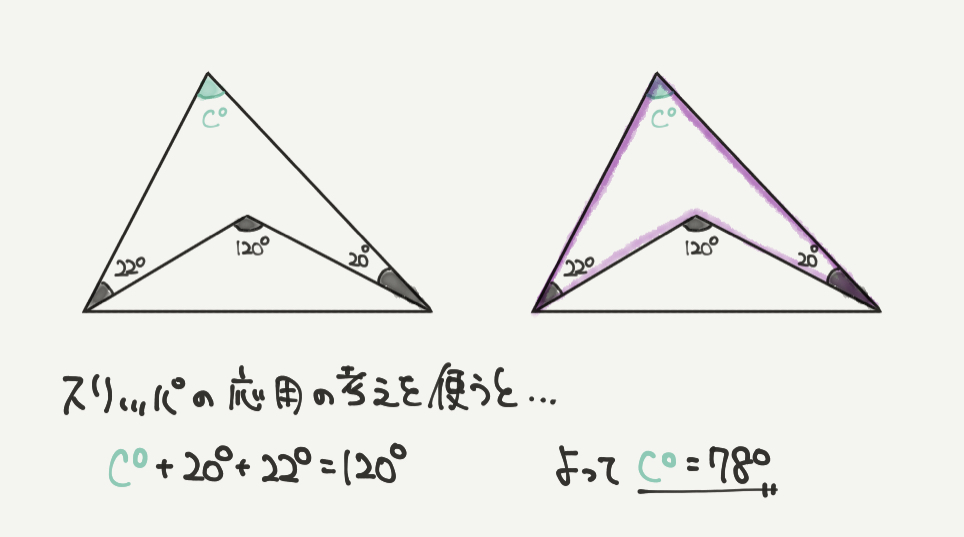

最後にc°を求めましょう。
c°はスリッパの応用の考えを理解していればすぐに解くことができます。
スリッパの形の応用の復習
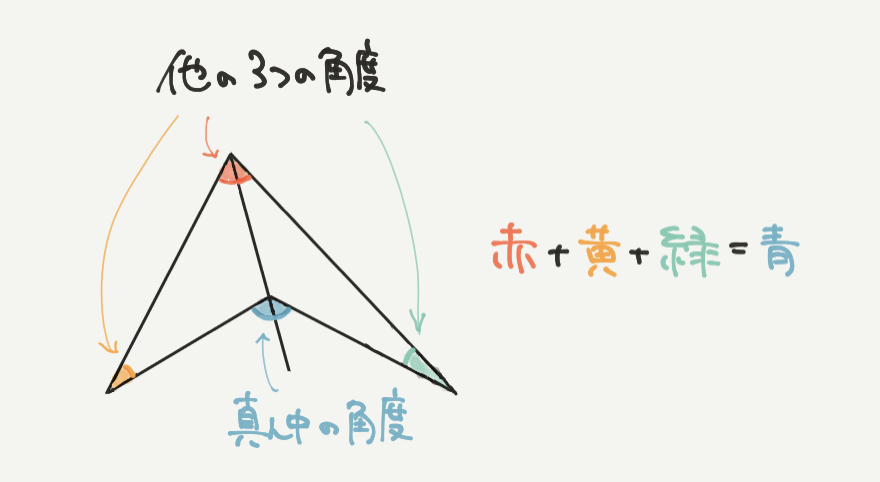

真ん中の角度がほかの3つの角度の和と同じという考え方を使うと…!!
c°+20°+22°=120°になりますので、
一発でcの角度を
120°-20°-22°=78°
c°=78°と出すことができます!
重なった2つの三角形から角度を求める問題のまとめ
今回の問題で大事なポイント
三角定規の基本(はじめに、STEP1)
スリッパの考え方(STEP2)
スリッパの考え方の応用(はじめに、STEP4)
以上で今日の問題はおしまいです。
たくさん覚えておくと楽なポイントを解説しましたがきちんと理解できたでしょうか?
今回の問題はむずかしくて絶対に解けないよ!っていうタイプではなく、
解けるけど時間かかっちゃう!というような問題だったと思います。
受験で大切なことは正解することももちろんなのですが、
それよりも「いかに早く、正確に解くことができるか?」という点が試されています。
なので、今回の問題を5分かけて正解できても、受験に合格できるかはわかりません。
むしろこういう知っていたらすぐに解けるような問題をいかに早く解けるかが受験では大切になってきます。
この記事のように他の問題でも、どうやったら早く計算できるのか?早く答えを出すことができるか?
という点についてていねいに解説しています。
ぜひ復習して今までよりも早く解くことを目標に勉強してみましょう〜!!



正解することも大事ですが、
試験時間内に早く正解することの方がもっと大事ってことです!!