はじめに
みなさんこんにちは!!
今日のテーマは前回と同じで、中学受験算数の「平面図形」についてです!
今回は複雑な形をした図形から面積と周りの長さを求める問題を解いてみましょう。
今日勉強する「補助線」の考え方を使ってむずかしい図形を知っている図形に変形していきましょう!
複雑な図形の周りの長さの求め方
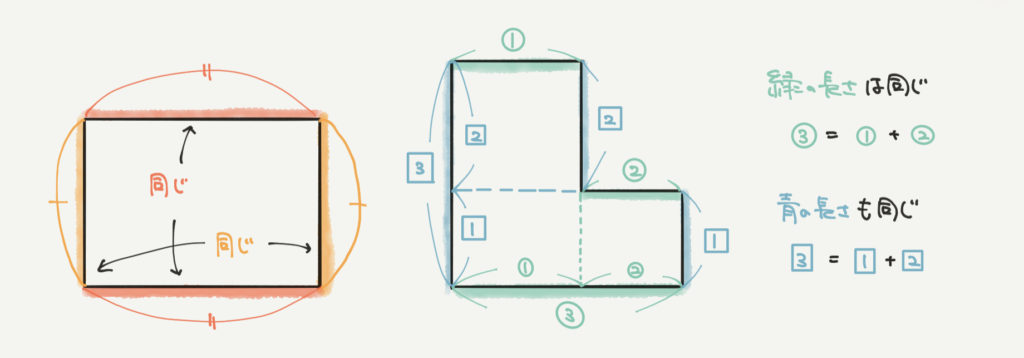
たとえば左の図のような普通の長方形を見てみましょう。
この図形の場合、赤い線の長さ(横)は2つとも同じになり、
黄色い線の長さ(たて)も2つとも同じになります。
では右の図のような複雑な図形の場合だとどうなるでしょう?
図形の形が変わっても考え方は同じです!
少しわかりやすくするために緑と青の補助線を書いています。
 わかみや先生
わかみや先生補助線は問題を解きやすくするために自分で書く線のことです。
今回は緑と青の点線が補助線になります!
補助線を引いてみると、①の部分と②の部分の長さが
③の部分の長さと同じであるとわかると思います。
同じように□1と□2の長さが□3の長さと同じであるとわかると思います。
ですので、緑の線の長さ(横)は2つとも同じになり、
同じように青い線の長さ(たて)も2つとも同じになります。
それでは問題を解いてみましょう!!
問題に挑戦!
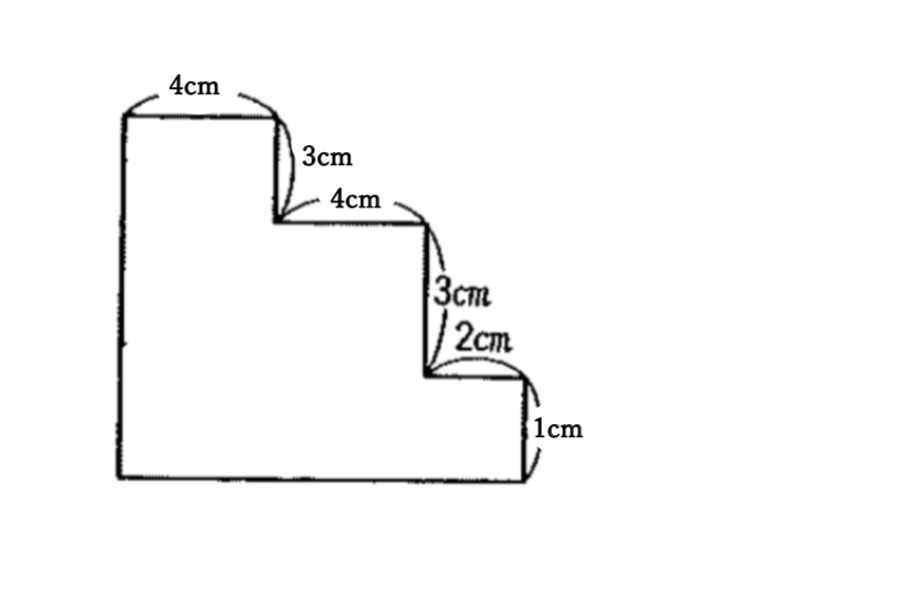

解答
答えを見るにはここをクリック!
まわりの長さ34cm
面積46㎠
この記事を書いている人はこんな人




解説を見てみよう!
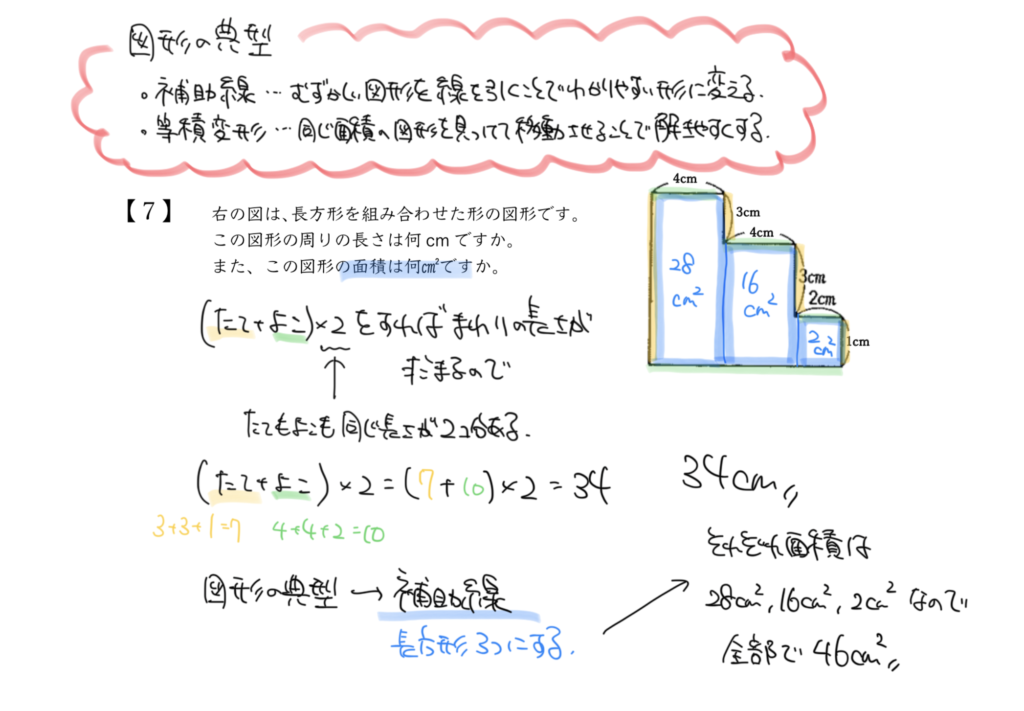

STEP1:複雑な図形のたてと横の長さを確認しよう
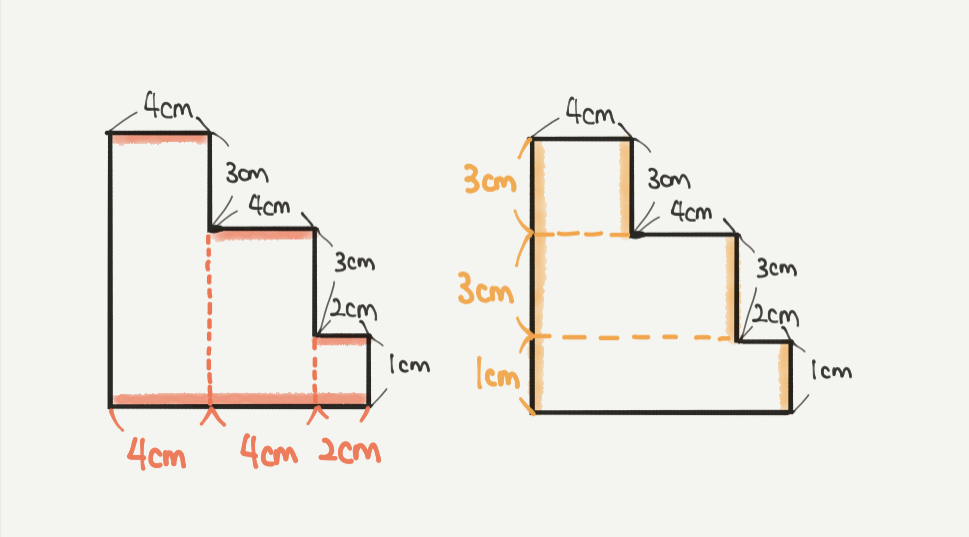

四角形がいくつも重なったような図形ですが、横の長さとたての長さに注目してみましょう。
それぞれ赤と黄色の補助線を引いていきます。
するとどちらの長さも2つあることがわかります。
横の長さも縦の長さも2つずつありますね!
STEP2:まわりの長さを計算しよう
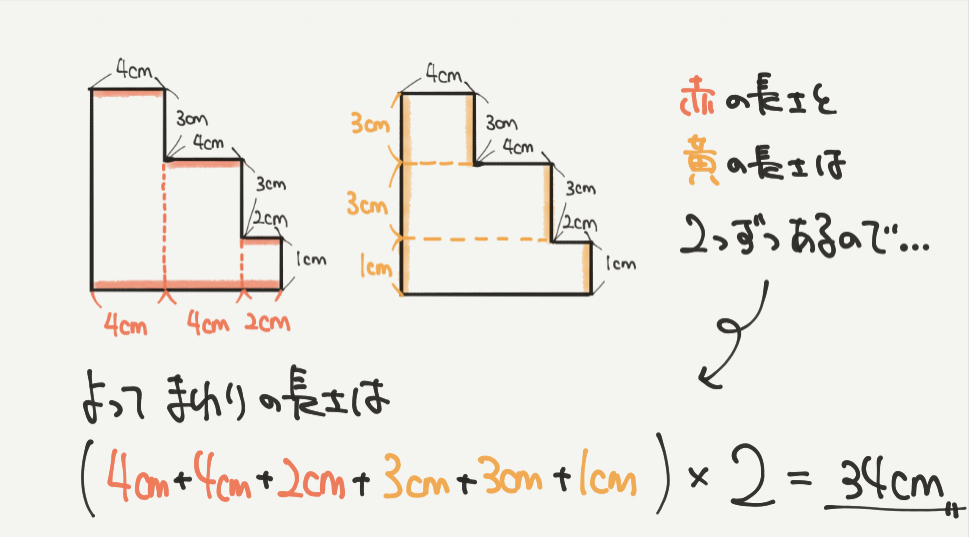

よってまわりの長さは「横+たて」×2で求めることができるので、
4cm+4cm+2cm+3cm+3cm+1cm=17cm
17cm×2=34cm
34cmと計算することができました!
STEP3:複雑な図形の面積も補助線を引いて考えよう
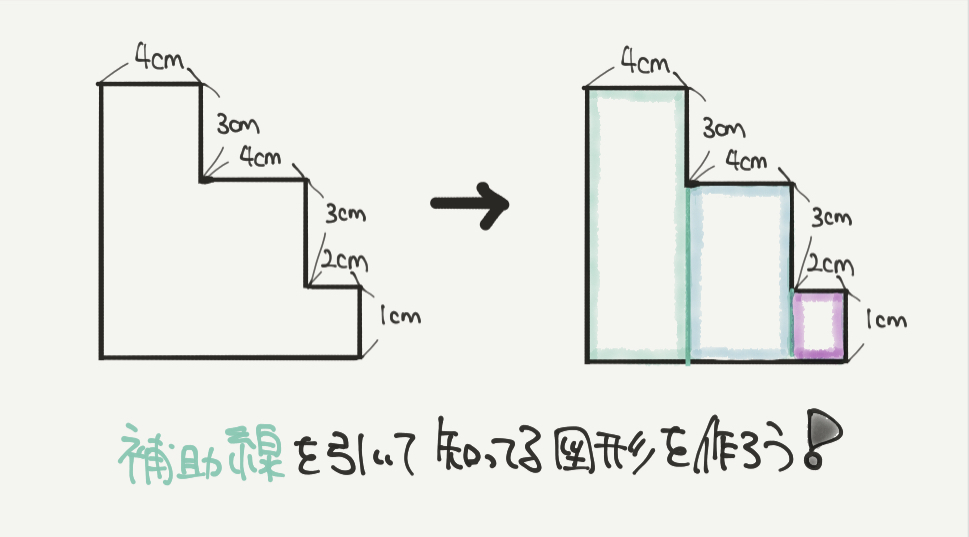

複雑な図形があっても、補助線を引いて自分の知っている図形に直していきましょう!
たとえばこの問題だと、複雑な図形に補助線を引いて、長方形を3つ作りました。
長方形なら面積を求めることができますね!
この複雑な図形は補助線を引くと、緑と青と紫色の長方形が3つ合わさった図形だとわかります!
この3つの長方形の面積を求めていきましょう。
STEP4:緑と青と紫の面積を求めよう
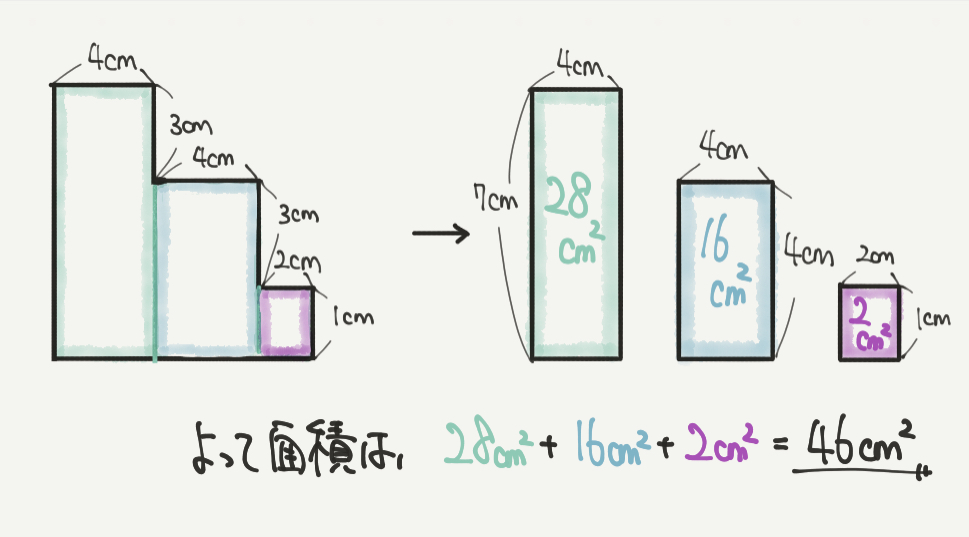

最後に面積を求めていきましょう。
STEP1で全ての辺の長さが求まっているので、かんたんだと思います。
緑の長方形:4cm×7cm=28㎠
青の長方形:4cm×4cm=16㎠
紫の長方形:2cm×1cm=2㎠
よってこの3つが合わさった複雑な図形の面積は、
28㎠+16㎠+2㎠=46㎠
となりました!!
複雑な図形の面積と周りの長さを求める問題のまとめ
今回の問題で大事なポイント
- 補助線の考え方(STEP1、2、3、4)
「同じところを見つける、作る」考え方(長方形の周りの長さは「たて+横」×2!)
以上で今日の問題は終わりです!!
いかがでしたでしょうか??いつもよりかんたんでしたか?
今回のような問題は、補助線を使う最も典型的な問題といってもいいかもしれません。
こんな図形はもう補助線引いてください!といっているようなものです笑
補助線は自分が解きやすい形にすることが何より重要ですので、
解説と全く同じ補助線じゃなくても問題は解けます。
「自分の知っている形」に直すことが大事です!
ちなみに長方形の周りの長さがたて+横の2倍になるのは
「さんすうがく」のはじめの方の問題でもやりましたね。
復習したい受験生は下の記事から解いてみてください!
長方形の「たて+横」についての復習
たてと横の差から長方形の面積を求めるには?

どんな図形にも使えるわけじゃないので注意!
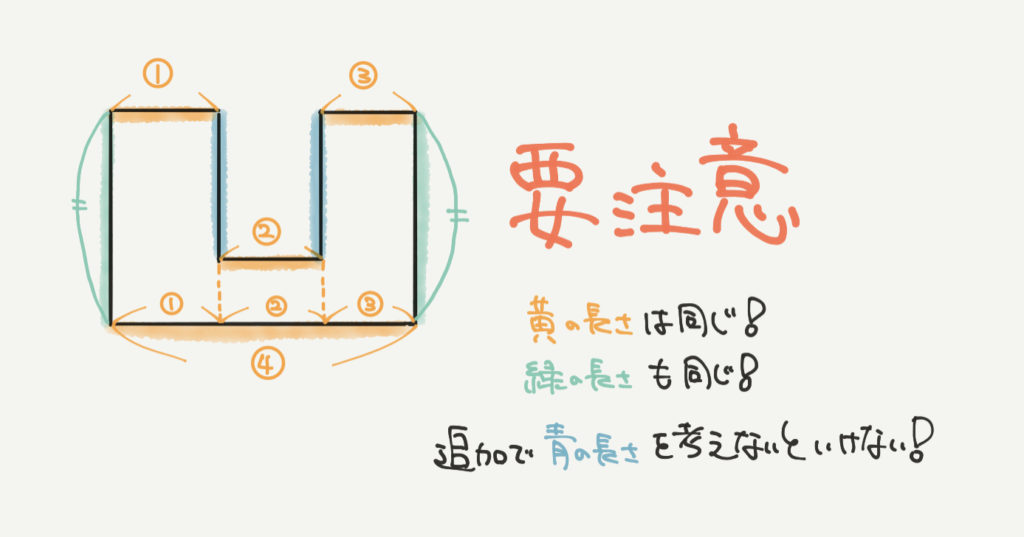

こういう図形だとさっきのやり方だけでは問題は解けませんので注意してくださいね!
なんでもかんでも図形のまわりの長さが「たて+横」2倍とは限りません。



ただやり方を暗記してしまうだけだと間違えてしまうので
気をつけてくださいね!