はじめに
みなさんこんばんは!!
今日のテーマは中学受験算数の「平面図形」についてです!
今回は五角形と六角形の問題を解いてみましょう。
五角形や六角形などの多角形の角度を求める問題は前に一度解説していますね!
はじめて「平面図形」に問題を解くよ!っていう受験生のみなさんは下の問題から解くと、
よりわかりやすく勉強することができます。
多角形の問題の復習はこちらから
多角形の内角の和を求めるには?
六角形と五角形のヒント
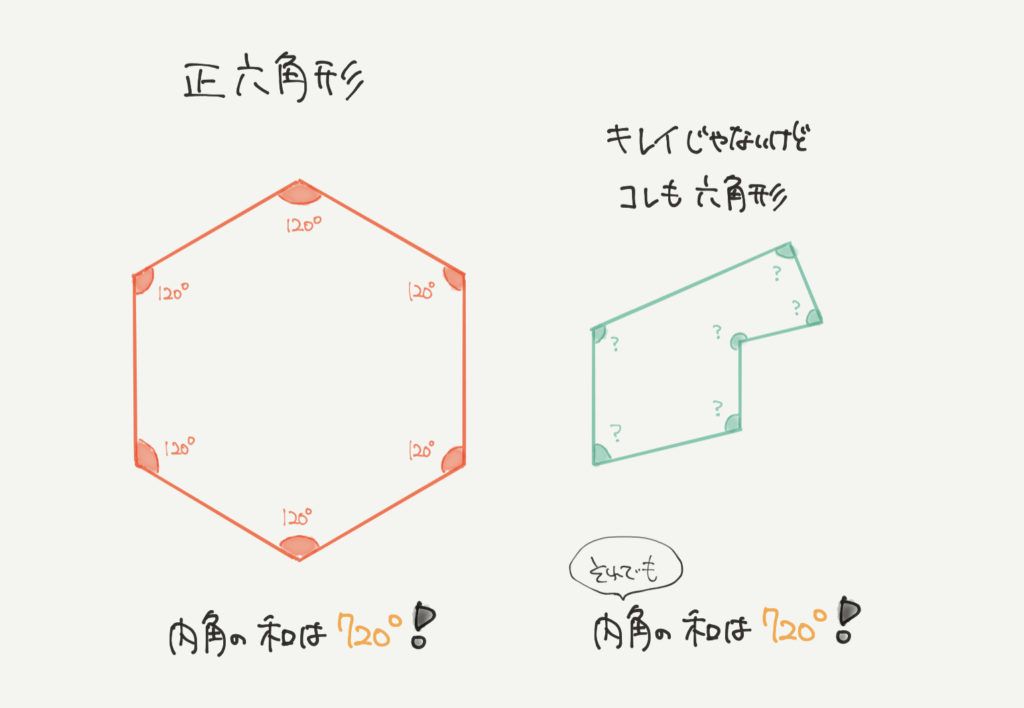
まずは六角形の内容からおさらいしておきましょう。
正六角形の場合、1つの内角は120°になりますね。そして内角の和は720°でした。
↑大事なポイントは上の記事で詳しく書いているので復習してみてくださいね。
緑の六角形の場合、正六角形ではないので1つ1つの角度の大きさはわかりませんが、
内角の和は必ず720°になりました。
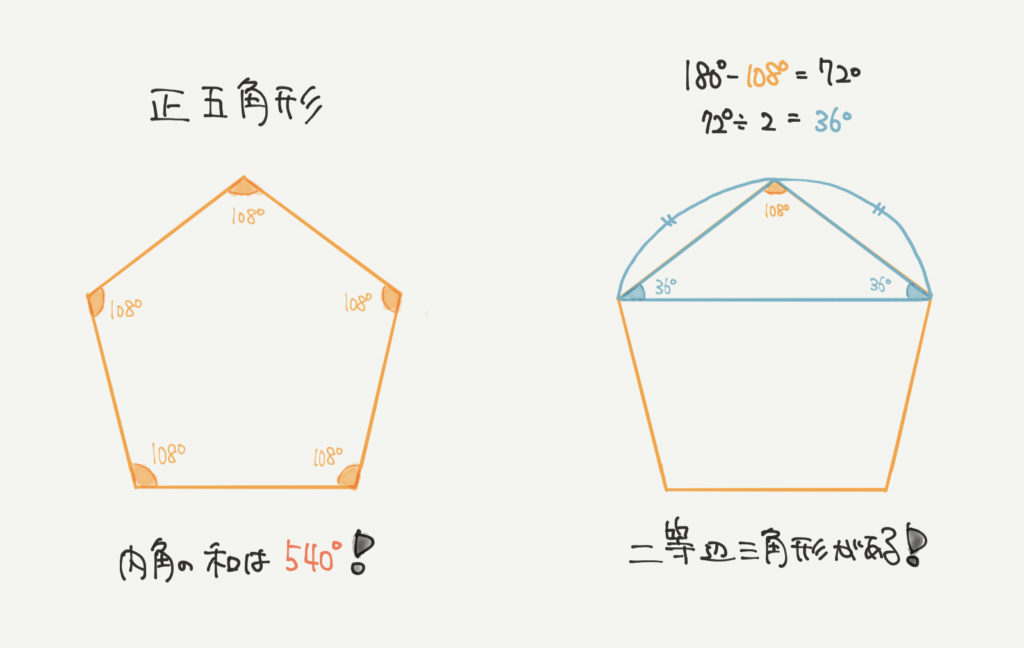
続いては正五角形についてのヒントになります。
正五角形は1つの内角は108°で、内角の和は540°でしたね。
今回の問題ではこの正五角形の中にある二等辺三角形が出てきますので、
今のうちにチェックしておきましょう。
1つの内角が108°なので、残り2つの角度は
180°-108°=72°(残り2つの角度の和)
72°÷2=36°(1つの角度)
36°、36°、108°の三角形とわかります。
 わかみや先生
わかみや先生今日解く問題はこれさえわかっていれば
かんたんに解くことができますので、
サクッと解いてしまいましょう!!
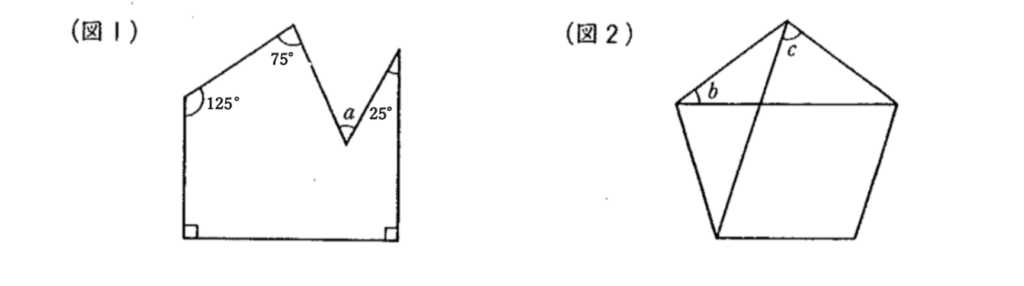
問題に挑戦!

解答
答えを見るにはここをクリック!
a=45度(45°)
b=36度(36°)
c=72度(72°)
この記事を書いている人はこんな人




解説を見てみよう!
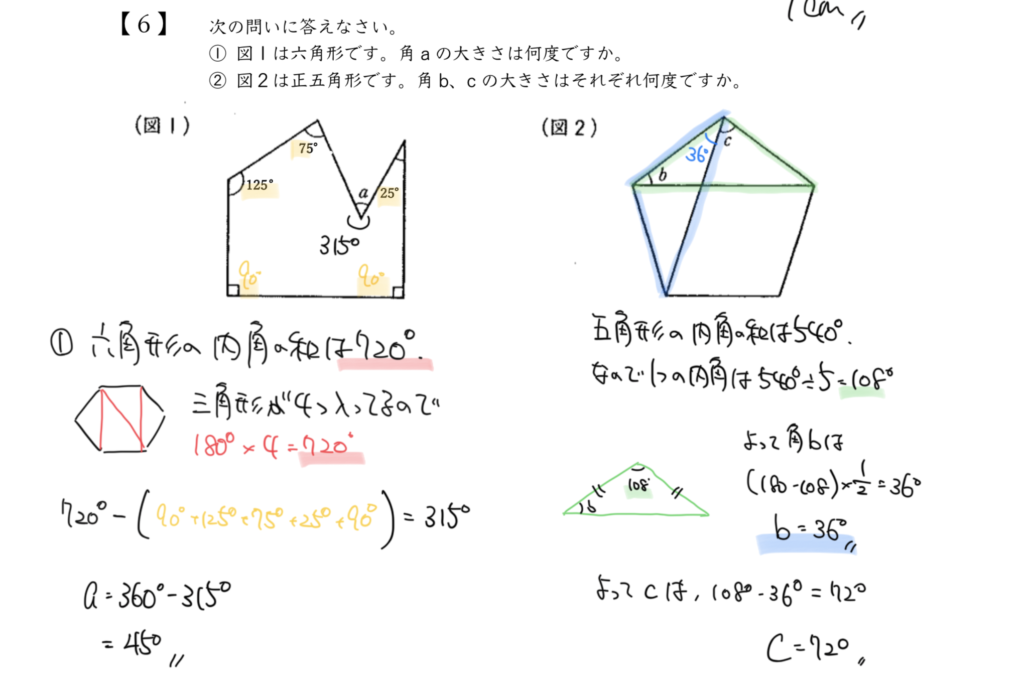

STEP1:五角形と六角形について確認しておこう
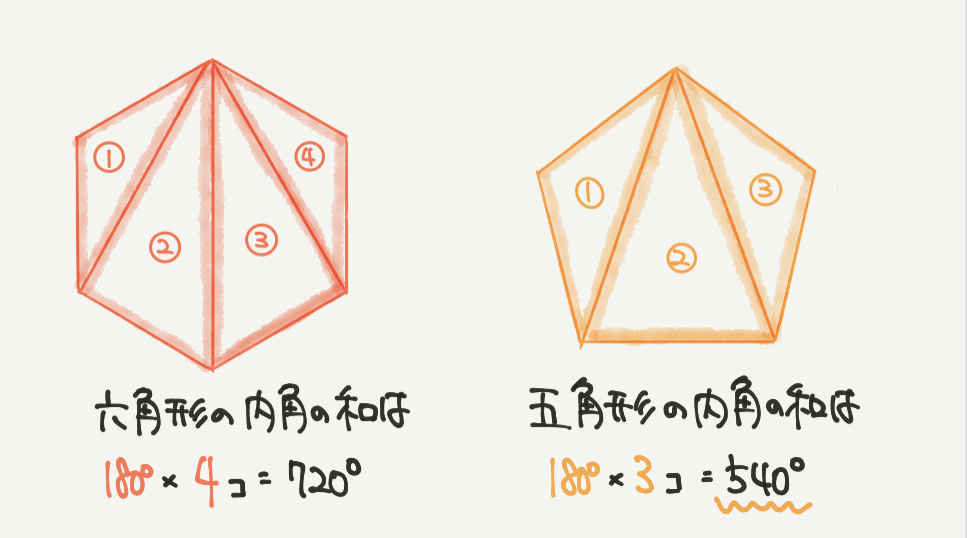

まずは五角形と六角形について確認していきましょう。
もうすでに分かってるよ!!という受験生はSTEP2から見てもらっても大丈夫です。
それぞれの内角の和をまずは求めていくと・・・
六角形の内角の和=720°
五角形の内角の和=540°
と求めることができますね!
多角形の内角の和は三角形が図形の中に何こあるのかで求めることができましたね!
さて、ここまで確認したらSTEP2へ行きましょう〜!
STEP2:aの角度を求めよう
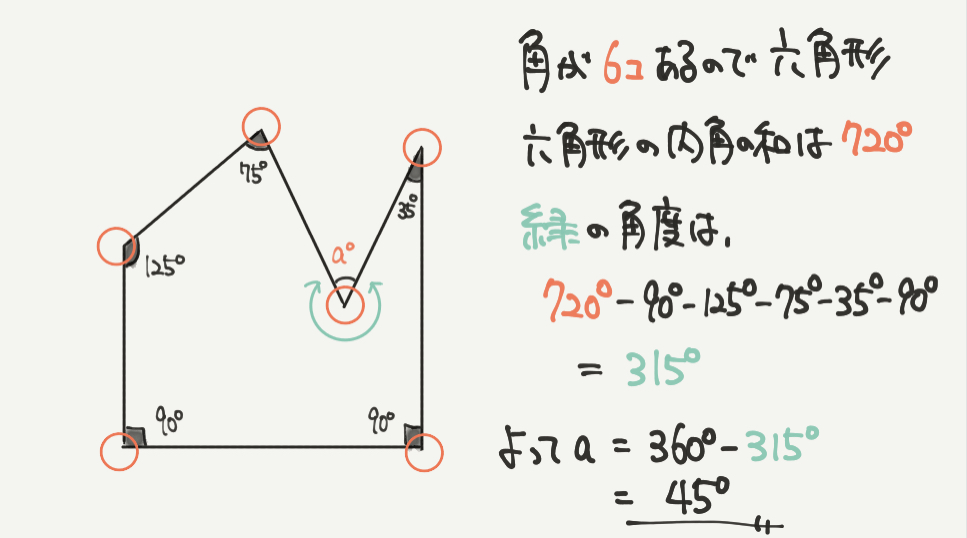

さて、STEP2では早速aの角度を求めていきましょう。
こんなよくわからない形でもこの図形には角が6つあるので、六角形になります。
六角形の内角の和は720°なので、問題文から緑の角度を求めていくと!
720°-90°-125°-75°-35°-90°=315°になります。
よって求めたいaの角度は
360°-315°=45°と計算できました!
STEP3:bの角度を求めよう
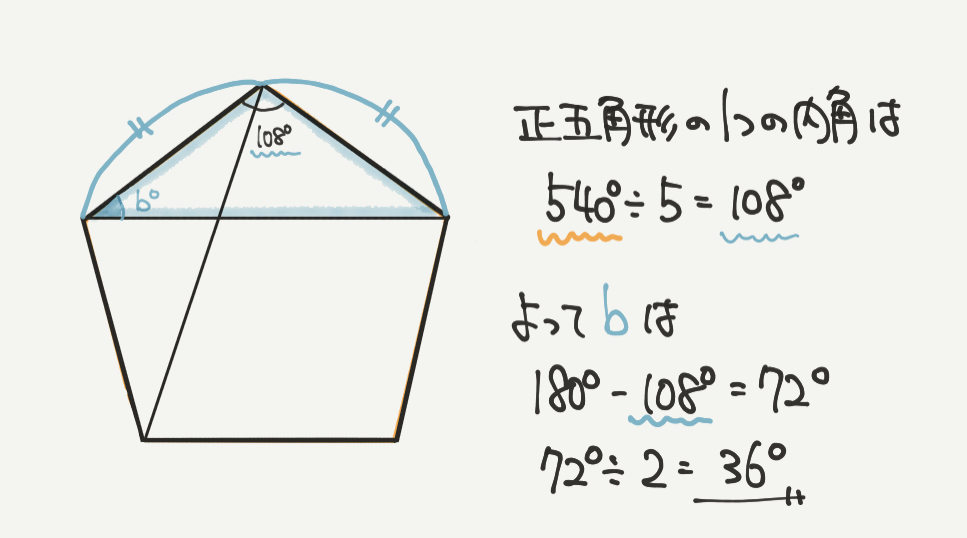

続いてbの角度を計算していきます。
こちらははじめにで説明した通りで、正五角形の中にある二等辺三角形に注目してもらえば
一発で解くことができます。
正五角形の1つの内角が108°なので、求めたいbの角度は36°となります。



正五角形の1つの内角が108°なので、
残り2つの角度は
180°-108°=72°(残り2つの角度の和)
72°÷2=36°(1つの角度)だったね!
STEP4:cの角度を求めよう
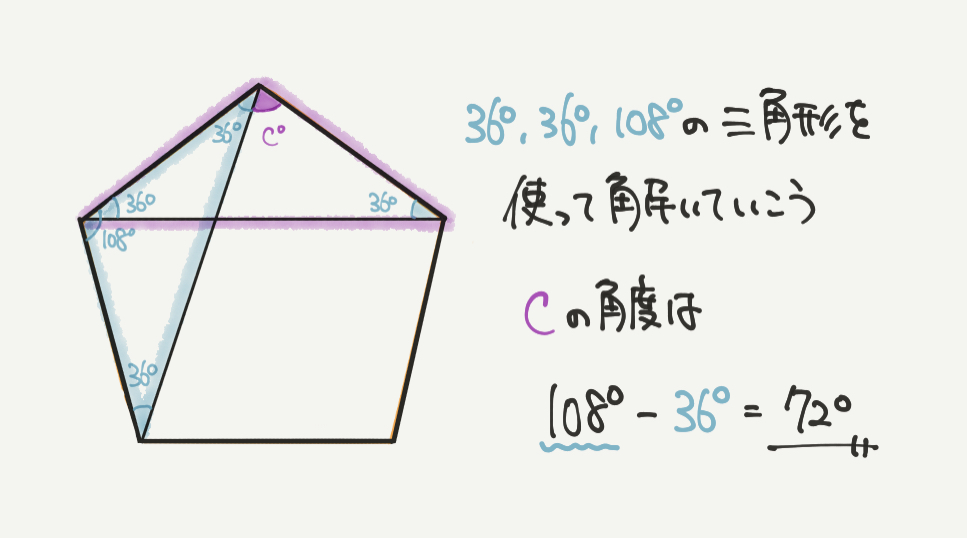

最後にcの角度を求めましょう。
cの角度を計算するのもそこまでむずかしくはないと思います。
STEP3で求めた36°、36°、108°を使って計算していくと・・・
cの角度は108°-36°=72°になります!!
六角形と正五角形の角度を求める問題のまとめ
今回の問題で大事なポイント
- 五角形の基本(はじめに、STEP1、2)
- 六角形の基本(はじめに、STEP1、3、4)
- 「同じところを見つける・作る」考え方(STEP3)
・今回は二等辺三角形を求めよう!
今回の問題はこちらでおしまいです!!
今までの問題よりも少しかんたんだったと思いますがいかがだったでしょうか??
どうでしょう?少しは図形が得意になってきたでしょうか?
今回の問題では五角形や六角形の基本をおさえることができればかんたんに解けたと思います。
平面図形の問題は他の算数の問題と違って、「知っていればすぐに解ける」ポイントが多いと思います。



他の問題も解きながらしっかりとポイントを
おさらいしておきましょう!!