【中学受験攻略】直角三角形の辺の長さの簡単な求め方とは？平面図形のポイントを徹底解説！

はじめに

みなさんこんにちは！！
今日のテーマは中学受験算数の「平面図形」についてです！

今回挑戦ちょうせんする問題はいつもと違ちがい、図形の長さを求めるような問題です。
今までの角度を求める問題よりもパズルのような面白おもしろさがあります。

算数が苦手な受験生でもわかるようにていねいに解説していますので、
一緒いっしょに問題を解いていきましょう！

今回も「長さを求めることができるポイント」について解説していますので、
下のヒントからみていきましょう！

30°、60°、90°三角形の秘密ひみつ

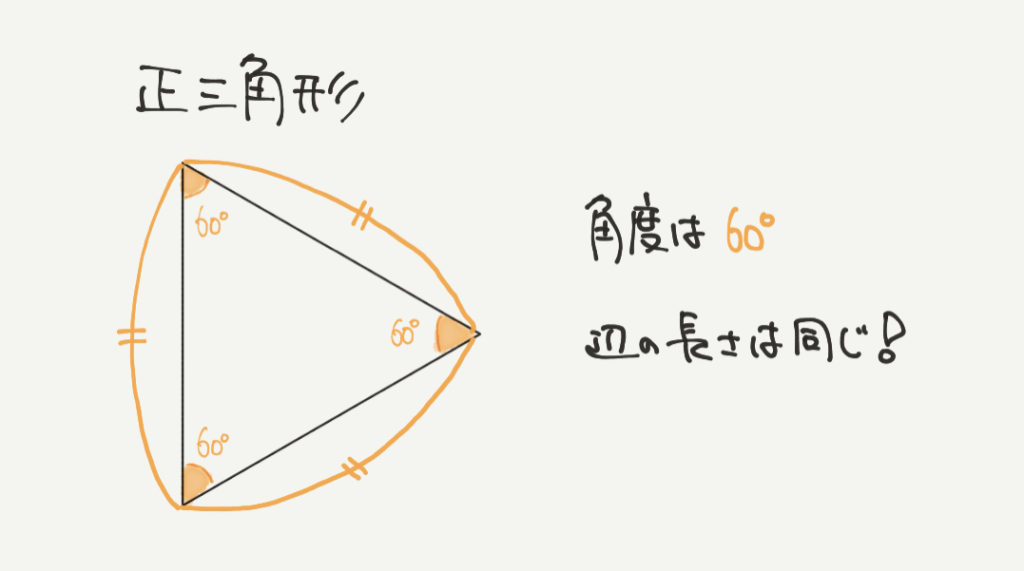
まずは正三角形についての復習からです。
正三角形には以下のような特徴とくちょうがありましたね。
・それぞれの角度は60°
・それぞれの辺の長さは同じ

この正三角形を半分に切った形が30°、60°、90°三角形になります。

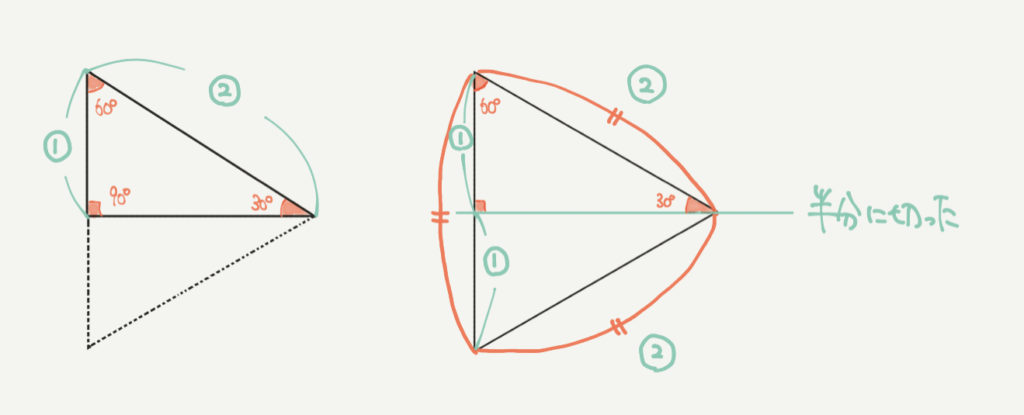
正三角形の辺の長さを②とすると、正三角形の全部の辺の長さが②になります。
そして半分に切った部分の長さは①になりますので、
30°、60°、90°三角形のときの長い辺と短い辺の長さの比は②:①=2:1になります。

今回の問題ではこの30°、60°、90°三角形の辺の比（2:1）の情報を使って
問題にチャレンジしてみましょう〜！

問題に挑戦ちょうせん！

下の図の三角形ABCは直角三角形で、角Bは60度です。
また、APは辺BCに垂直で、PQは辺ACに垂直すいちょくです。PQの長さは何cmですか。

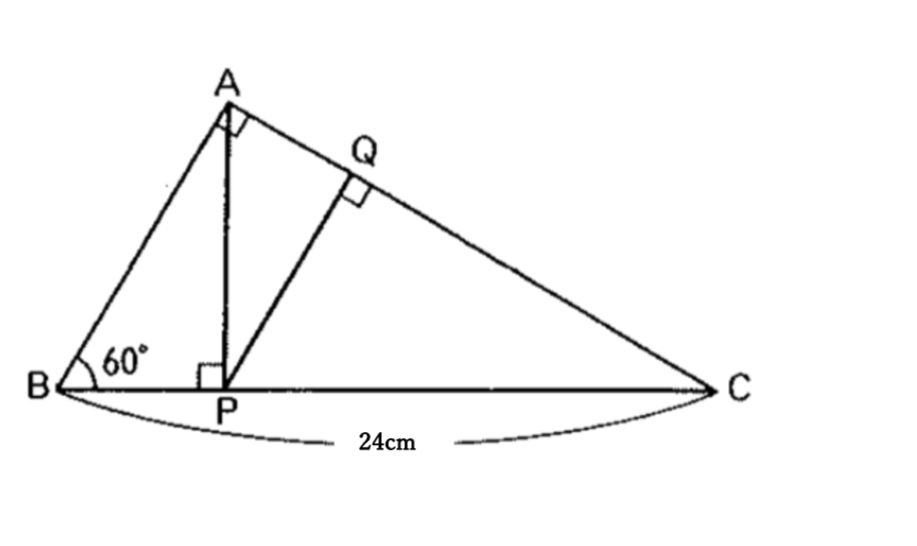
解答

この記事を書いている人はこんな人

解説を見てみよう！

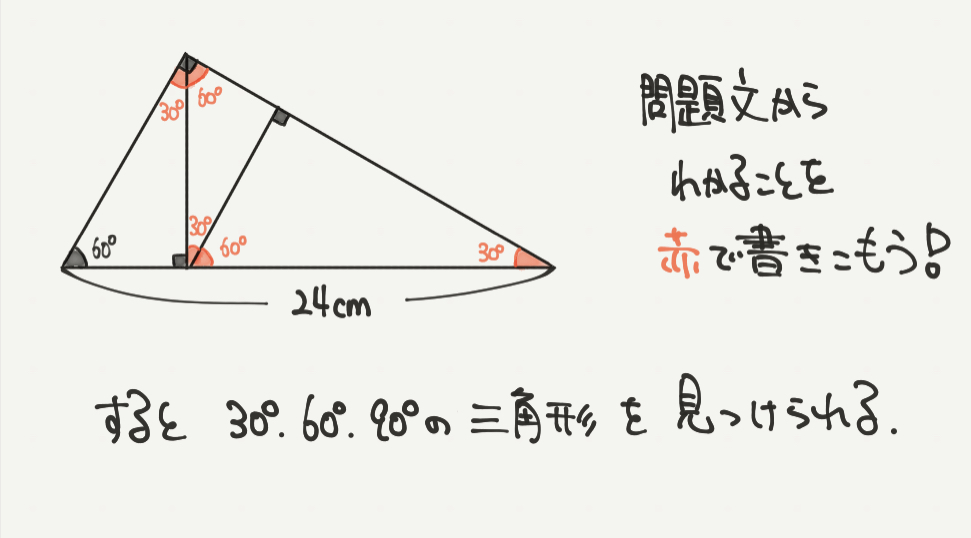
STEP1：問題文からわかることを図に書きこもう

今回の問題は知っていればすぐに解けますのでサクサクいきましょう！！
まずは問題文の内容を図に書きこみましょう。
この問題では、60°という情報がありますので、
三角形の内角の和（180°）から引いて赤い角度を求めていきましょう。

↑赤い角度を求める順番です。これ以外の順番でも求めることができます！

△は三角形という意味です。△ABCなら、三角形ABCを見てもらえればわかると思います！
赤い角度をきちんと全部書くことができればSTEP1はクリアです。

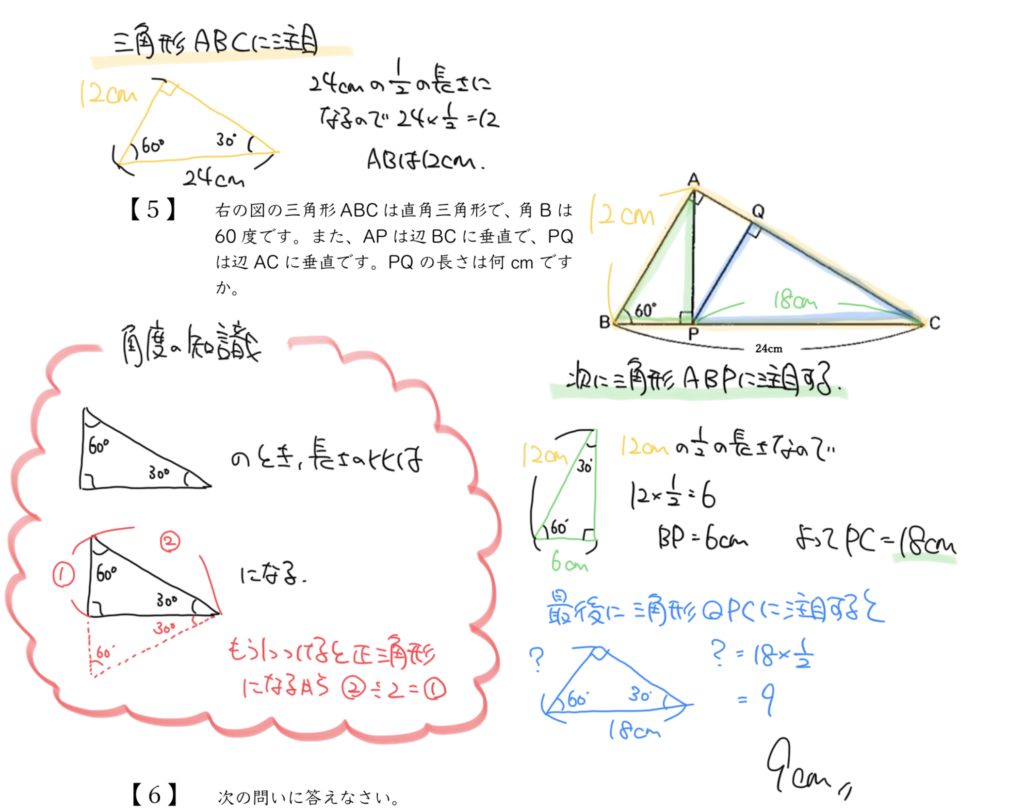
STEP2：ABの長さを求めよう

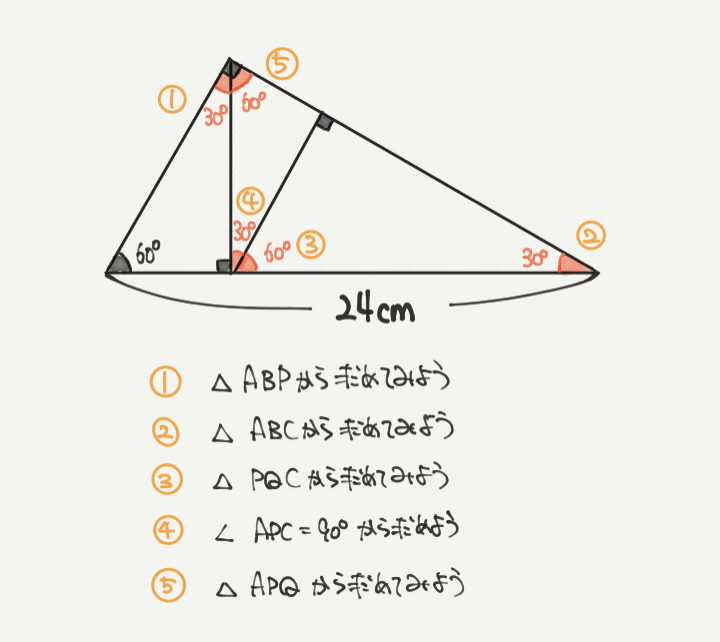
STEP2では30°、60°、90°三角形の辺の比を使ってABの長さを求めていきます。
まずは黄色の三角形に注目しましょう。

そして30°、60°、90°三角形の辺の比2:1に合わせて考えると、
ABの長さは、24cm×1/2=12cmとなります。

同じようにSTEP3、STEP4もやっていきましょう。

STEP3：BPの長さを求めよう

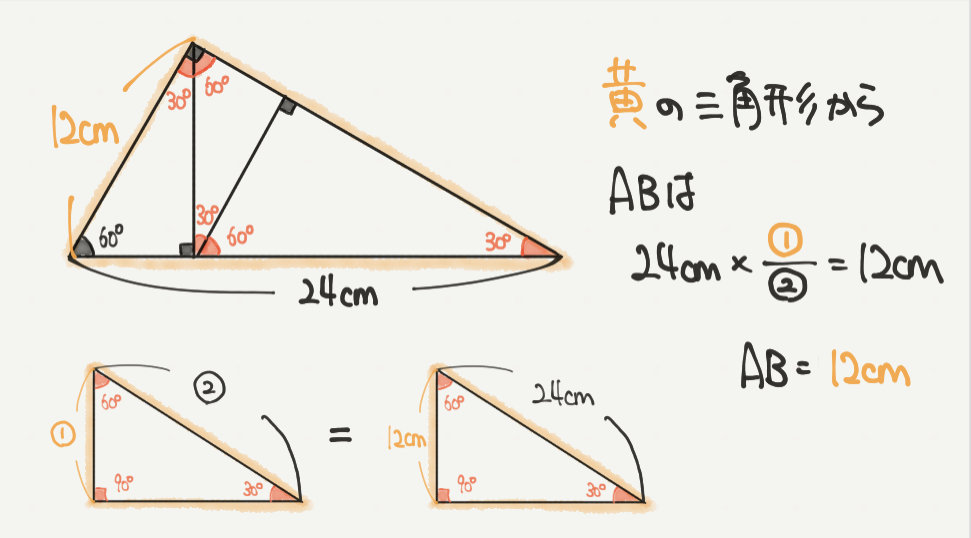
次はBPの長さを出しましょう。
注目する三角形は緑の三角形です。

30°、60°、90°三角形の辺の比を使って解くために緑の三角形の形を回転させておきましょう。

30°、60°、90°三角形の辺の比2:1に合わせてSTEP2と同じように考えると、
BPの長さは、12cm×1/2=6cmとなります。

STEP4：PQの長さを求めよう

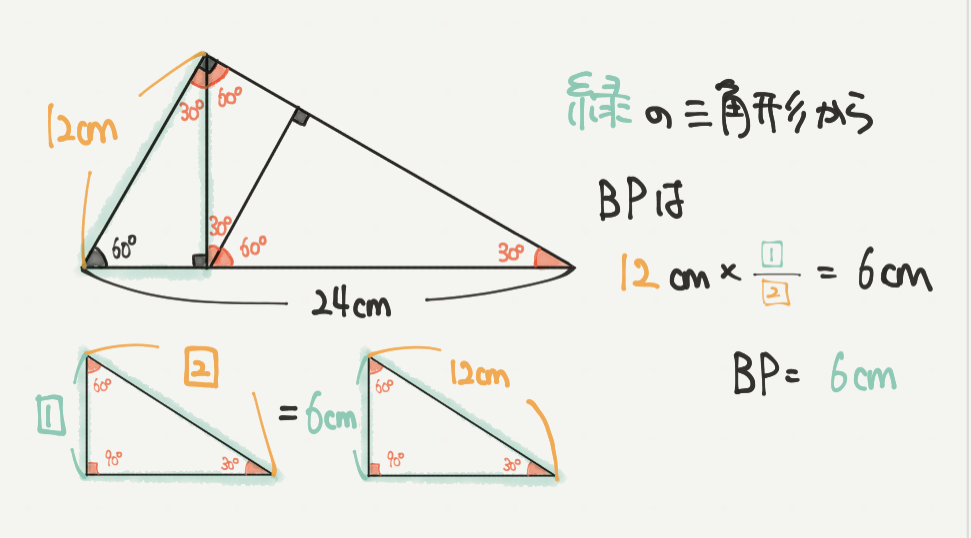
最後に答えであるPQの長さを出していきましょう。
STEP3までの情報を図に書き込むと、12cmと6cmが図にかけると思います。

知りたいPQの長さも30°、60°、90°三角形の辺の比を使って解けそうですが、
そのために必要な長い辺の長さ（PC）をまずは求める必要があります。

STEP3でBP=6cmとわかっているのでPCの長さは
24cm-6cm=18cmとなります。
よってPQは18cmの半分になるので、
18cm×1/2=9cmと求めることができました。

直角三角形に垂線すいせんを引いた時の辺の長さを求める問題のまとめ

今回の問題で大事なポイント

• 30°、60°、90°三角形の秘密ひみつ（辺の長さの比を確認しておこう）
  
• 「同じところを見つける」考え方（STEP1、2、3、4）
  　・30°、60°、90°三角形をたくさん見つけよう！

いかがでしたでしょうか？
今回の問題は今まで以上に「知っていればすぐに解ける問題」だったと思います。

気をつけてもらいたいのは、この辺の比が2:1になるのは30°、60°、90°の三角形のときだけです！

何でもかんでも三角形の辺の長さの比が2:1になるわけではないので気をつけてくださいね！！