【中学受験攻略】 平面図形のコツ！重なった台形の一辺の長さの求め方とは？

はじめに

みなさんこんばんは！！
今日のテーマは、中学受験算数の「平面図形」についてです！
今回は重なった長方形からある部分の長さを求める問題を解いてみましょう。

今日の問題は「平面図形」の単元の中でも少しむずかしいかもしれません！
いつもよりもていねいに解説していますので、一緒に見ていきましょう！

台形の面積の求め方

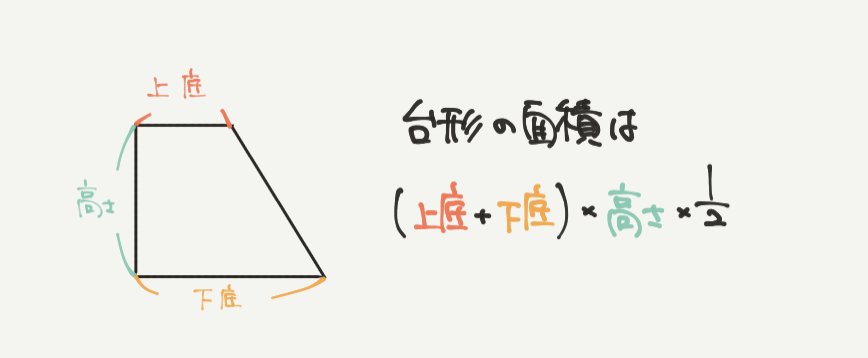
まずは台形の面積の求め方を復習しておきましょう！
台形の面積は
（上底じょうてい＋下底かてい）×高さ×1/2で求めることができます。

上底じょうていとは台形の上の辺のことで、下底かていは台形の下の辺のことです。

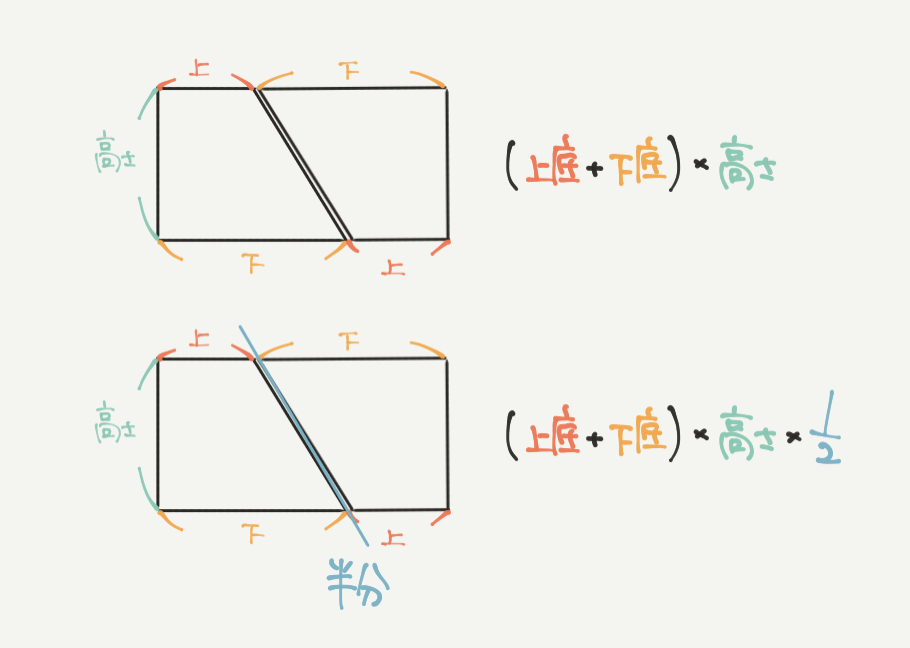
台形の面積は四角形の面積を半分にすることで求められます。
同じ形の台形をひっくり返して重ねると、大きな長方形を作ることができます。

この長方形の面積の横の長さは上底じょうてい＋下底かていになり、たての長さは高さになります。
そして知りたい台形の面積は大きな長方形の半分なので、
（上底じょうてい＋下底かてい）×高さ×1/2となりました！

図形を重ねると線分図ではどうやって書ける？

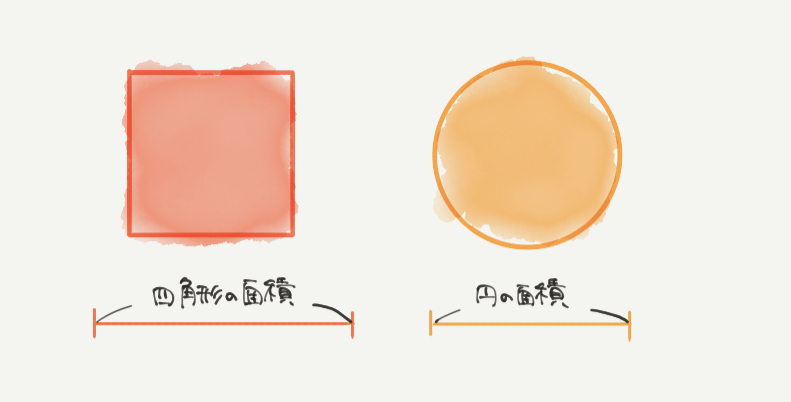
次に図形を重ねたとき、線分図をどのように書くことができるのか考えてみましょう。
たとえば、四角形と円があったとします。

2つの図形の面積はそれぞれ線分図でかんたんに書くことができると思います。

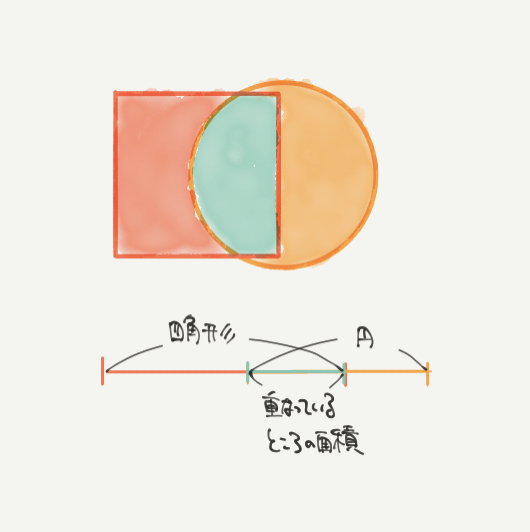
ではこの2つの図形が重なるとどうなるでしょうか？
四角形と円は少し重なり、線分図が重なることがわかると思います。

なので線分図も少し重ねて書くようにしましょう。
それぞれ対応している部分を赤、緑、黄色で書いているのでよくみてみてください。

今日解く問題はこのポイントを理解していれば解くことができます！
さっそく問題にチャレンジしていきましょう。

問題に挑戦ちょうせん！

下の図は、2つの長方形を重ね合わせた図形です。
この図形全体の面積が622㎠のとき、xの長さは何cmですか。

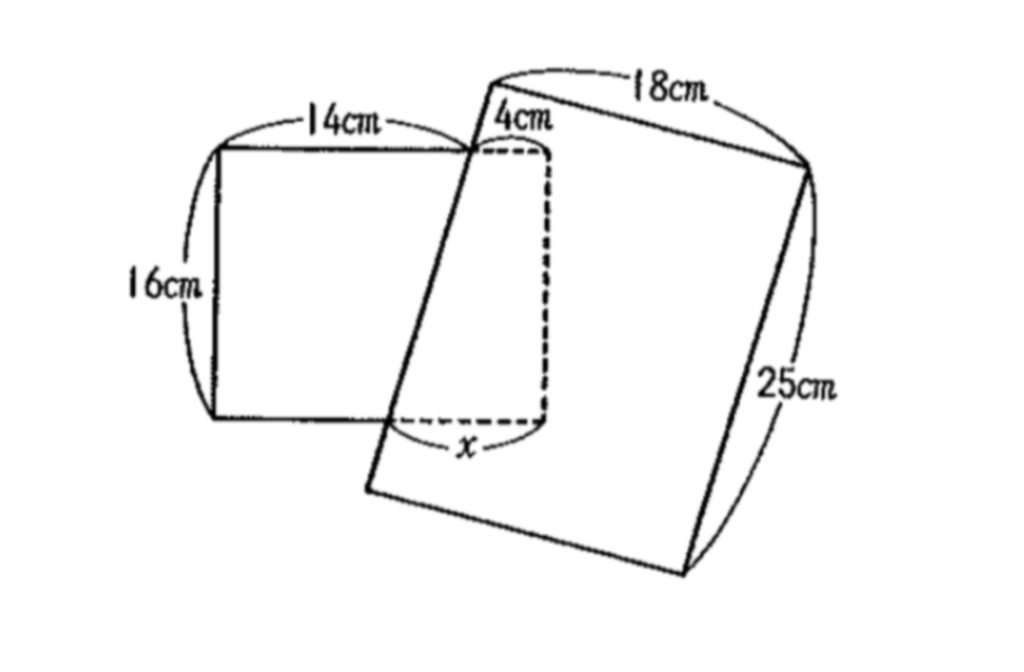
解答

この記事を書いている人はこんな人

解説を見てみよう！

STEP1：重なっている図形に注目しよう

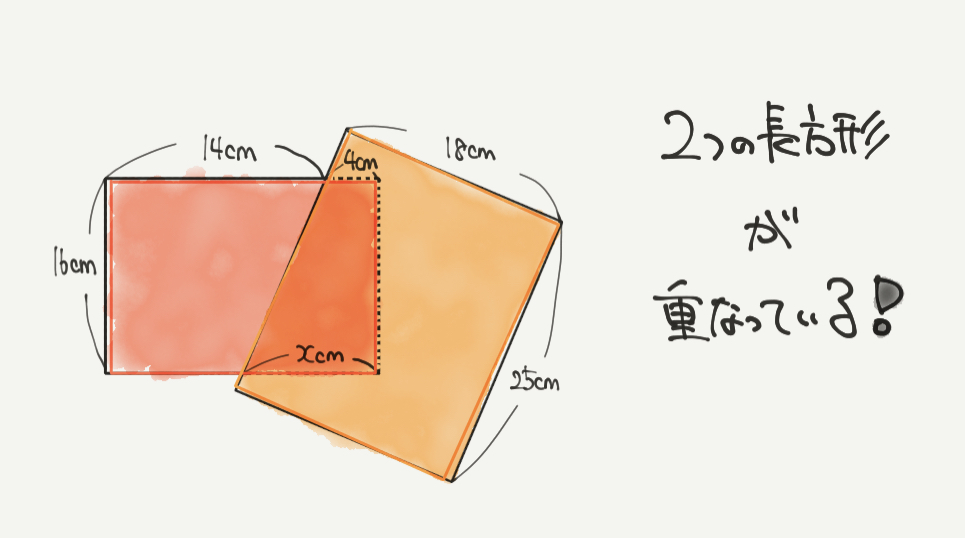
まずはSTEP1！問題文を見て2つの長方形が重なっているとわかると思います。

そうです！重なっているといえばさっきの重なっていた線分図を思い出してみましょう。

さて、ここからSTEP2で問題文の図からわかることを書きこんでいきましょう。

STEP2：問題文からわかることを書いていこう

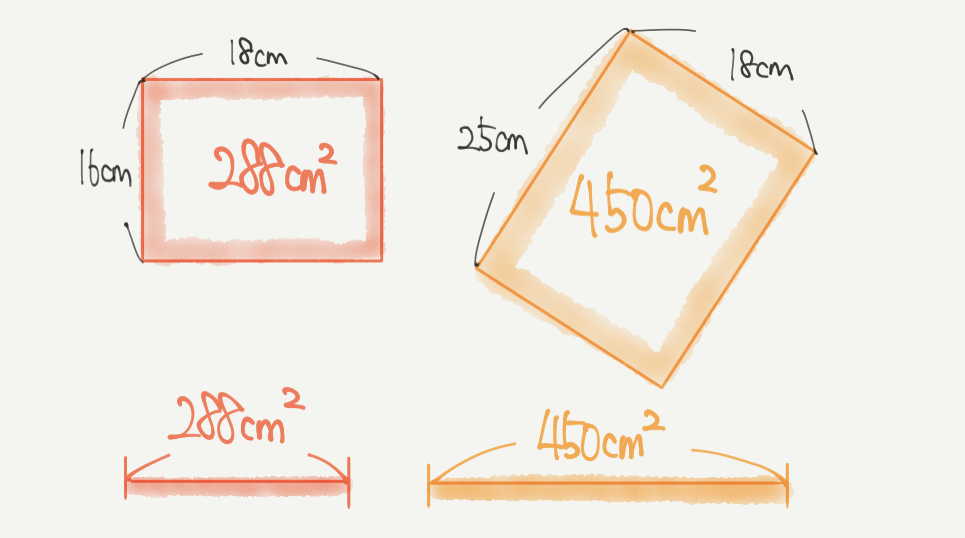
さて、次にそれぞれの図形の面積を求めていきます。

赤い四角形の面積は、
16cm×18cm=288㎠

黄色い四角形の面積は、
25cm×18cm=450㎠

とかけるので、線分図もこのように書けると思います。
さあここからが大事なポイントです！

STEP3：重なった台形の面積を求めよう

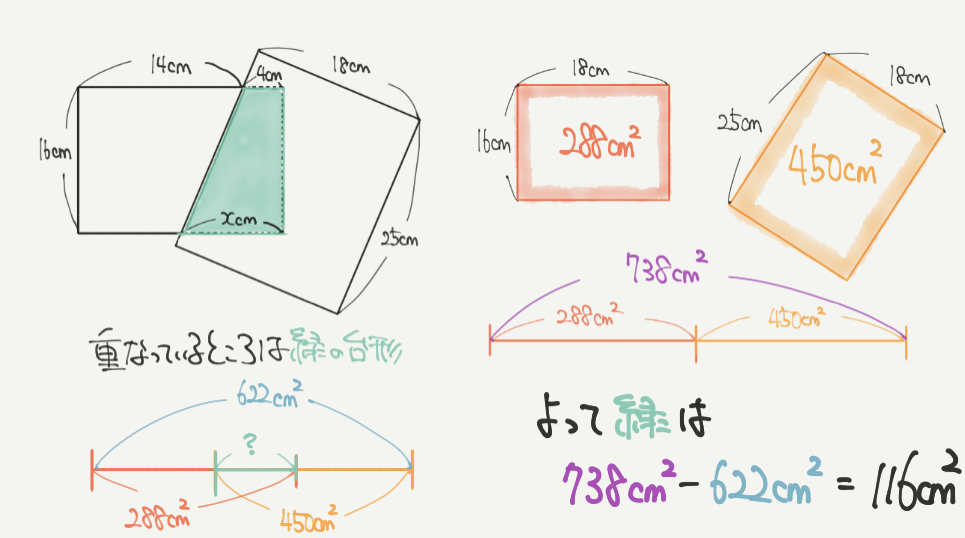
STEP2で2つの長方形の面積を求めましたので、重なった台形の部分の面積を求めてみましょう。

重なった図形の面積は622㎠と問題文で言われています。

しかし、赤い四角形と黄色い四角形の面積の合計は
288㎠+450㎠=738㎠になります。

この738㎠と622㎠の差の部分こそ、
重なっている緑の台形の面積だということがわかります！

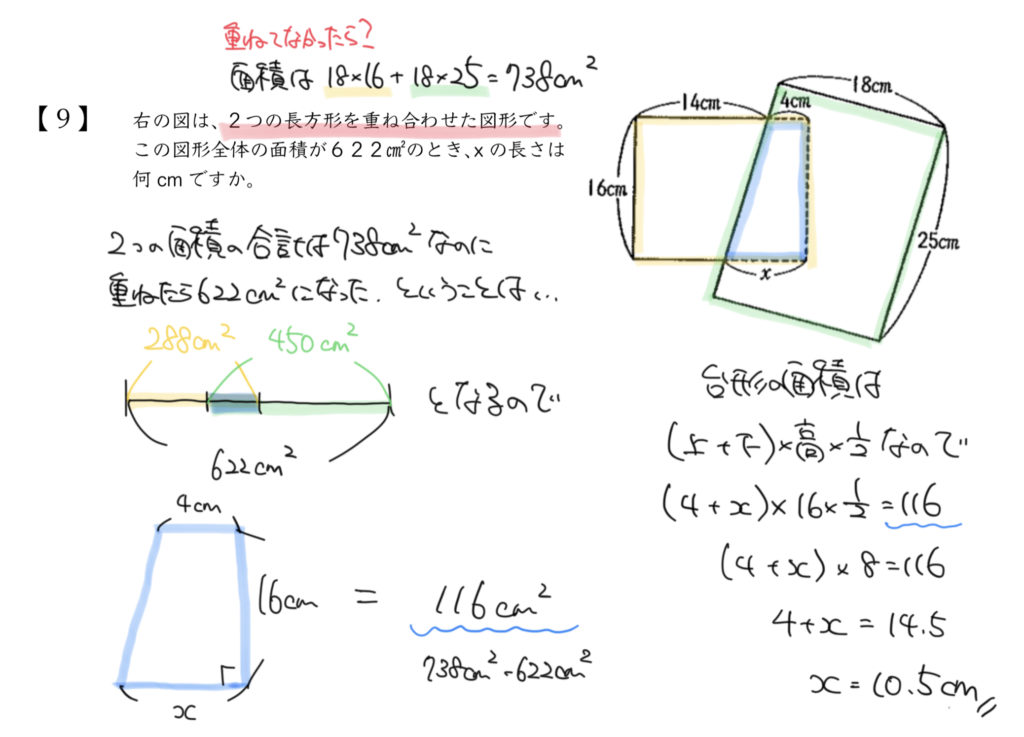
よって台形の面積は、
738㎠–622㎠=116㎠と計算できます。

STEP4：台形の面積から答えを求めよう

最後は台形の面積から下底かていの長さを求めるだけです。
台形の面積は、「（上底じょうてい＋下底かてい）×高さ×1/2」だったね！！

よって今回の台形だと、
（4cm+xcm）×16cm×1/2=116㎠になるので

（4cm+xcm）×16cm=116㎠×2
（4cm+xcm）=116㎠×2÷16cm

4cm+xcm=14.5cm
よってxの長さが10.5cmとなりました。

↓計算があやしい受験生は下の解説も見てみてください！

重なった台形部分の一辺の長さを求める問題のまとめ

今回の問題で大事なポイント

• 台形の面積の求め方（はじめに）
  　・（上底じょうてい＋下底かてい）×高さ×1/2
• 図形が重なるときの考え方（はじめに、STEP3）
  　・線分図に正しく面積を書いてみよう！

以上で今回の問題は終わりです！！きちんと理解できましたか？
今回の問題のポイントでは2つの長方形が重なってしまっていることでした。

特にSTEP3の部分、線分図にきちんと問題文の内容を書けるか、
書けないかが正解するかどうかの分かれ道だったと思います。

普通ふつうに赤の四角形と黄色の四角形を足すと738㎠になって、
問題文の662㎠と違ちがってくるのでそこの数字にあれ？っと気づければむずかしくなかったと思います。

重なっている考え方は平面図形の問題ではこれからも出てきます！