【中学受験攻略】平面図形のコツ！円の中の斜線部分の面積と周の長さを簡単に求める方法

はじめに

みなさんこんにちは！！
今日も中学受験算数の「平面図形」について一緒に見ていきましょう！
今回は円の問題に挑戦してみましょう！

円の問題は苦手という受験生も安心してください！
今日勉強する「計算のまとめ方」を使って計算を楽に早く解いてみましょう〜。

円の問題は計算を楽にすることが大切！

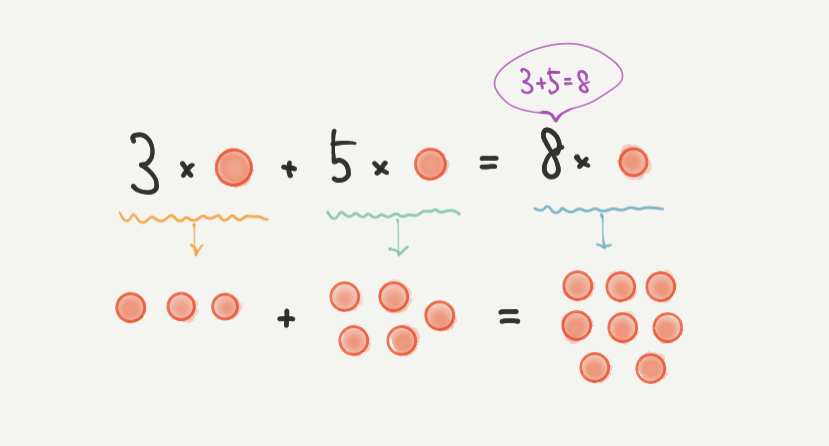
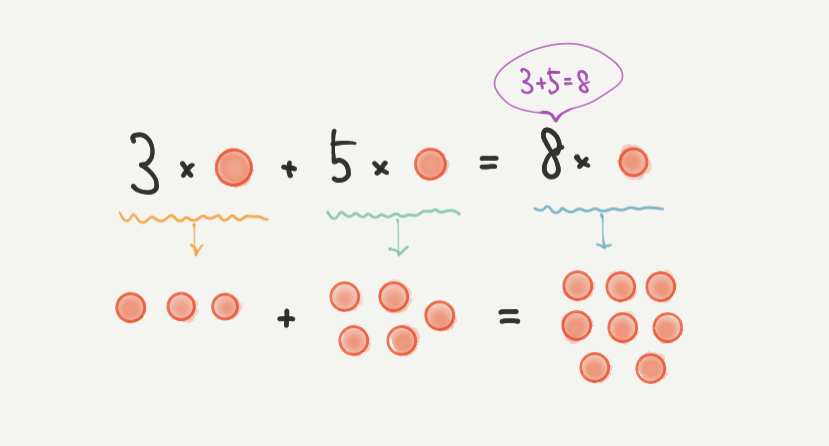
円の問題を解く前に、かんたんなポイントを紹介しょうかいします。
このやり方を覚えると、計算スピードがグッと早くなるのでとてもおすすめです！

たとえばこちらの図で、
3×●+5×●という式があったとします。

このときの計算は、（3+5）×●と楽にすることができます。

実際に絵をかいてみて確かめてみましょう！

上の図にように、3×●を●●●とかいて、5×●を●●●●●と書いてみると
足し合わさった●の数は8個こになるのがわかると思います。

なので、3×●+5×●=8×●と計算を楽にすることができました。

3.14の計算は絶対楽に解いたほうがいい！●=3.14で考えてみよう

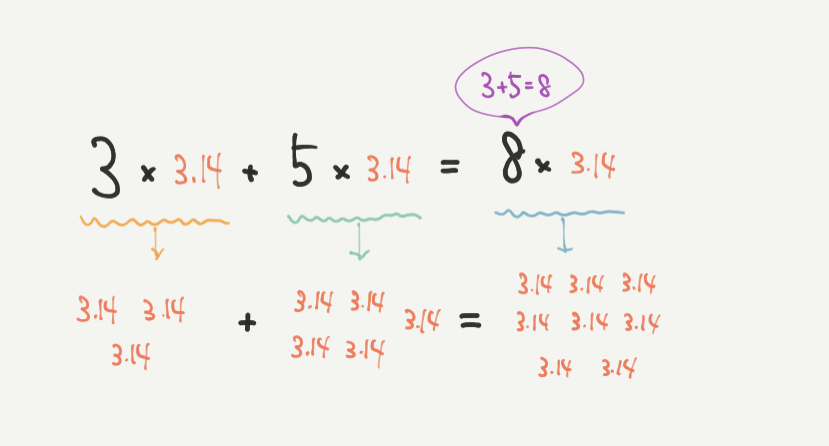
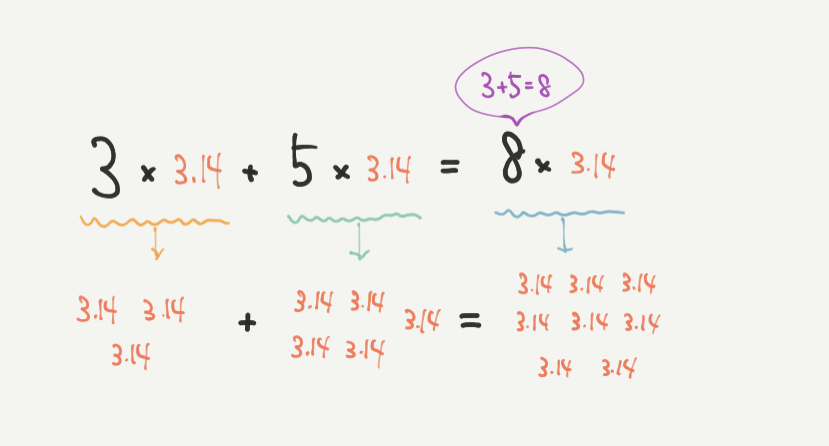
さっきと全く同じ式で、●を3.14に変えてみました。

このときもかんたんに計算することができます。

●だとわかるのに、●が3.14になると計算できなくなってしまう受験生がたくさんいます。
対応している部分を色で分けているので、ぜひここできちんと理解しておきましょう！

式は以下の通りになります！

やってはいけないのは、1つ1つの式を計算して足し合わせるようなやり方です。

このやり方だと3.14の計算を2回もしないといけないですし、
最後の足し算もケアレスミスしてしまう可能性かのうせいがたくさんあります。

一方で、計算を楽にするやり方であれば、8×3.14で1つの式で答えを出すことができます。

このように計算を楽にすることは、ケアレスミスをなくすことにもつながります。

今回に問題は、この楽して計算する方法を使って問題を解いていきましょう。

問題に挑戦ちょうせん！

下の図は、直径20cmの円の中に半円を二つ書き入れたものです。
円周率を3.14として次の問いに答えなさい。

① 斜線部分のまわりの長さは何cmですか。
② 斜線部分の面積は何㎠ですか。

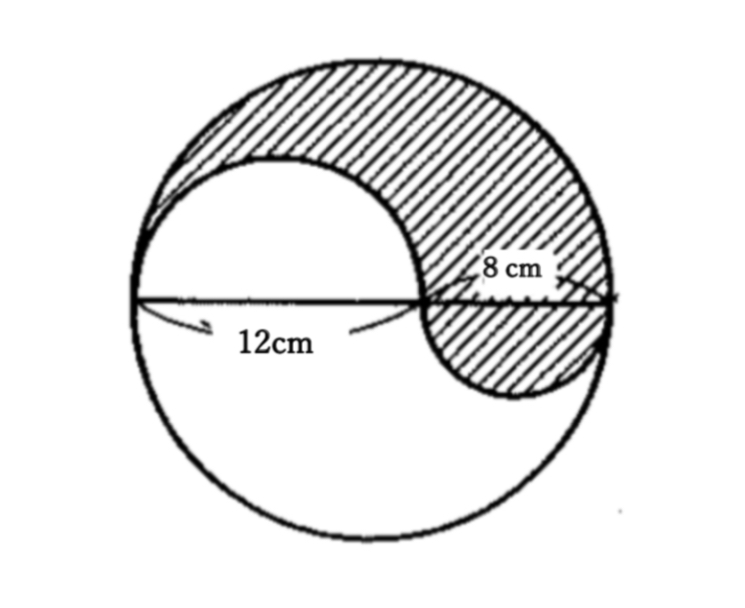
解答

この記事を書いている人はこんな人

解説を見てみよう！

STEP1：円周は赤＋黄＋緑

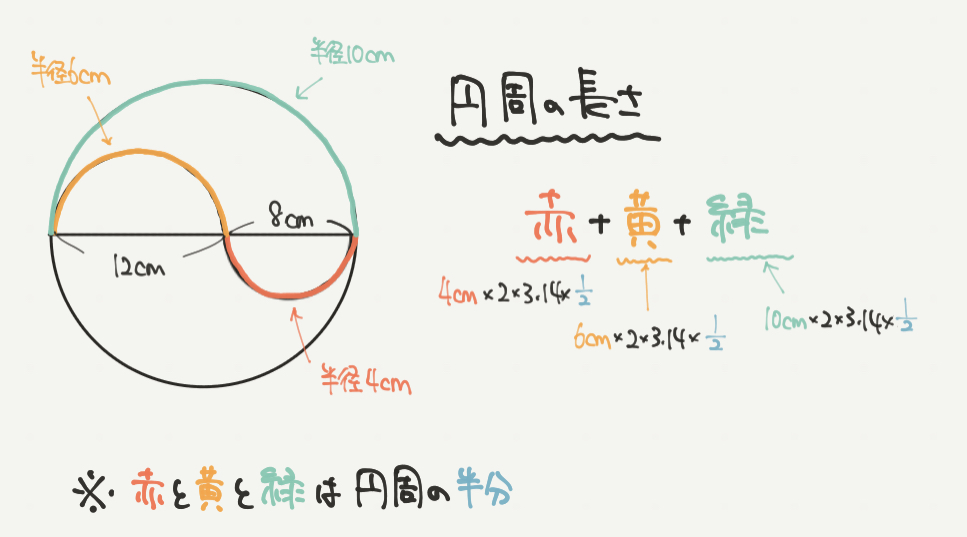
まずは斜線部分しゃせんぶぶんの周りの長さを求めていきましょう。

周りの長さは図の赤＋黄＋緑の部分を全部足した数になることがわかると思います。
1つ1つ計算する前に！まずはそれぞれの円周の式を書いてみましょう。

赤：4×2×3.14×1/2
黄：6×2×3.14×1/2
緑：10×2×3.14×1/2

↑この長さは円周の半分なので×1/2を忘わすれないようにしましょう。

STEP2：円周の長さを計算を楽にして求めよう

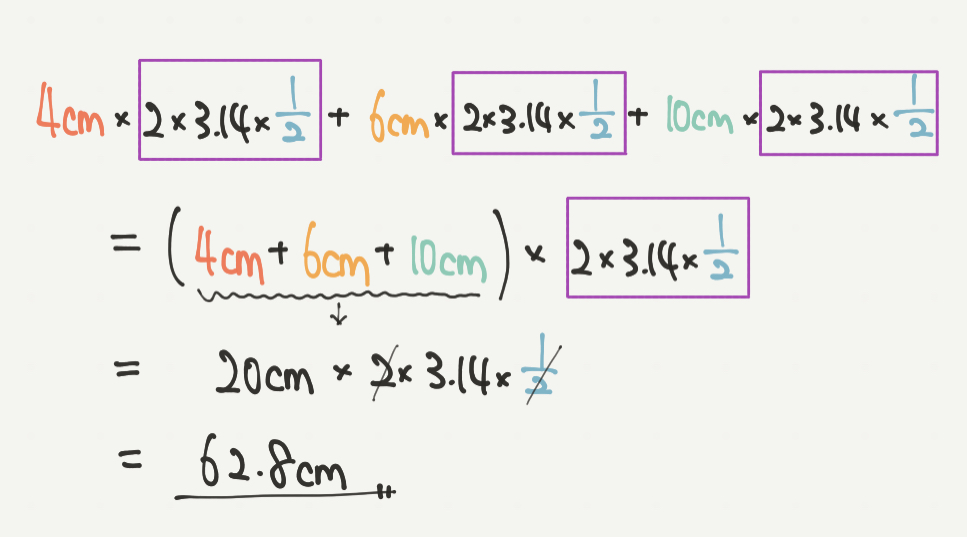
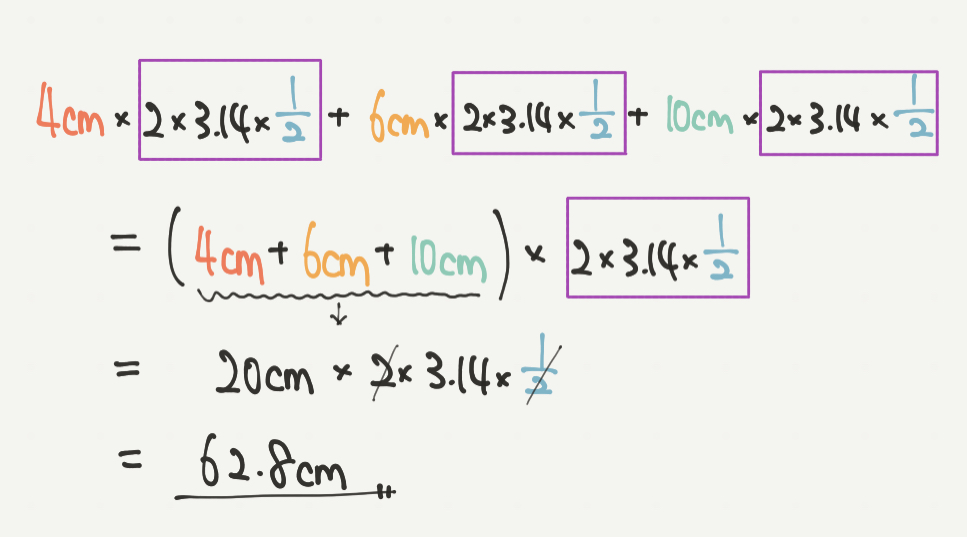
このとき、紫の部分が全部の式で同じになります。
はじめにで勉強した計算をかんたんにするやり方を使って、
2×3.14×1/2=■として計算してみましょう。

4×■+6×■+10×■=　(4+6+10) ×■と楽に考えることができます。

よって求めたい周りの長さは、
(4+6+10) × ■
=20×■
=20×2×3.14×1/2

20×2×3.14×1/2
=62.8cmとなりました。

STEP3：面積は緑＋赤−黄

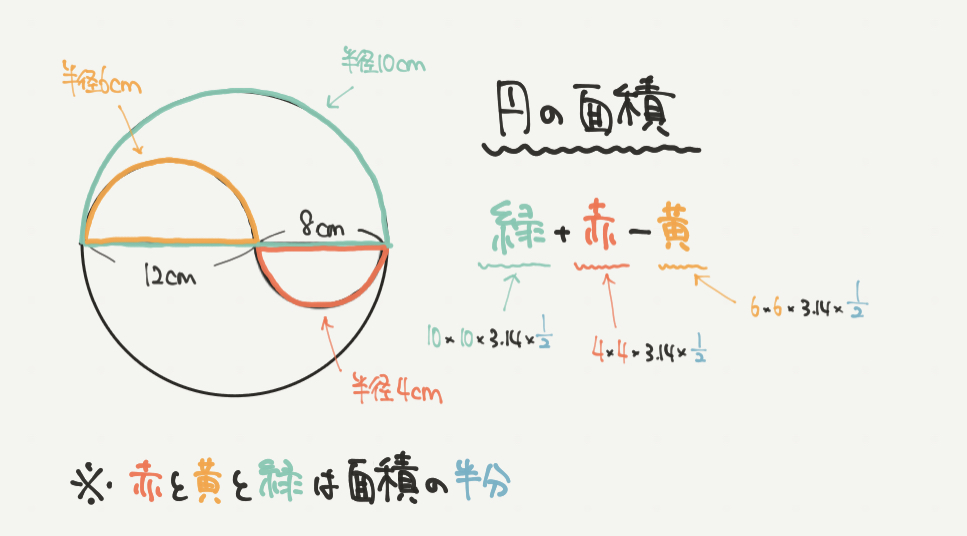
続いて斜線部分しゃせんぶぶんの面積を求めましょう。
この面積は緑の半円＋赤の半円−黄の半円で求めることができますね！

それぞれの半円の面積は、
緑：10×10×3.14×1/2
赤：4×4×3.14×1/2
黄：6×6×3.14×1/2

なので、この3つの式を使って計算していきましょう。

STEP4：円の面積を計算を楽にして求めよう

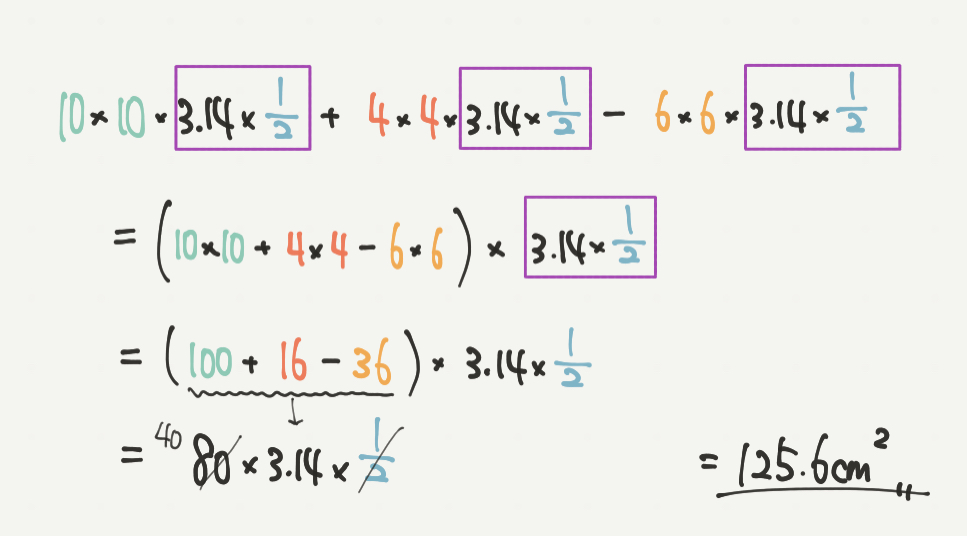
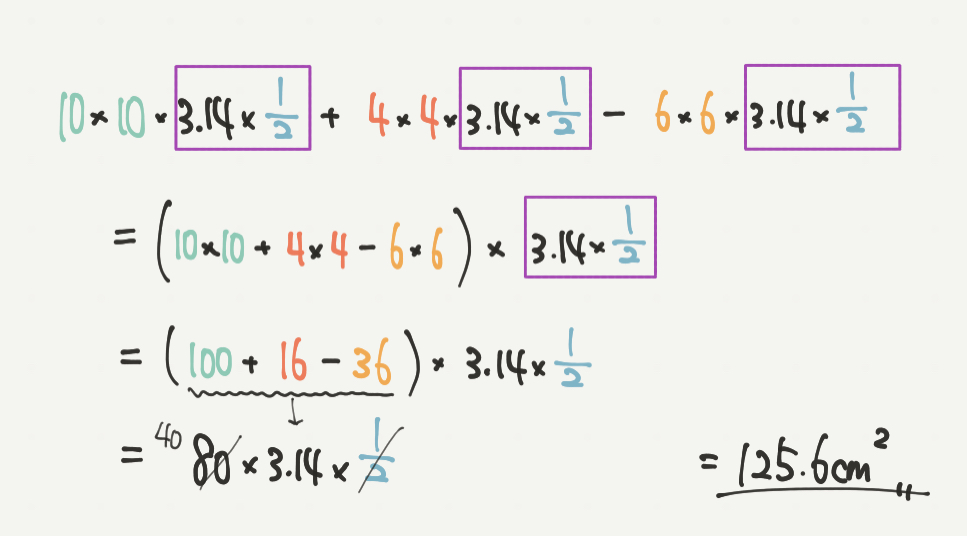
このときは、紫の部分が全部の式で同じになります。
なので、3.14×1/2=■として計算してみましょう。

10×10×■+4×4×■−6×6×■
= (10×10+4×4−6×6) ×■と楽に考えることができます。

なので、
(10×10+4×4−6×6) ×■
= (100+16−36) ×■
=80×■
=80×.14×1/2
=125.6㎠

と計算することができました。

円の中の斜線部分の周りの長さと面積を求める問題のまとめ

今回の問題で大事なポイント

• 計算を楽にする考え方（はじめに、STEP2、4）
  ・「同じところを見つける、作る」考え方を使って計算をまとめてしまおう！
  
• 円についての考え方
  ・円の面積の求め方の確認（半径×半径×3.14）
  ・円周の求め方（半径×2×3.14）

この問題のポイントはいかに楽に計算をするかでした。

特に3.14の計算はめんどくさいので最後にまとめて行うのが効率的こうりつです。
一つ一つ計算しても解けますが、それでは時間もかかってしまいますし、ミスもしてしまいます。

ですので3.14の計算を最後にまとめてやるために、楽する考え方をこの記事では勉強しましたね！

3.14の計算以外でもこの「まとめる考え方」をきちんと理解していれば同じ問題でも
解くスピードを上げることができます。