はじめに
みなさんこんばんは!
今日は前回やった問題とそっくりな、「割合と比」の問題にチャレンジしてみましょう!
「さんすうがく」をはじめて勉強する受験生にもわかるようにていねいに解説していますので、
一緒にがんばってきましょう!!
まずは線分図を書く練習をしてみよう
問題:次の①、②、③の内容を図にしなさい。
①AさんとBさんの所持金の比は5:4です。
②CさんからAさんとBさんは500円わたしました。
③すると、AさんとBさんの所持金の比が11:9になりました。
線分図の書き方
①の線分図
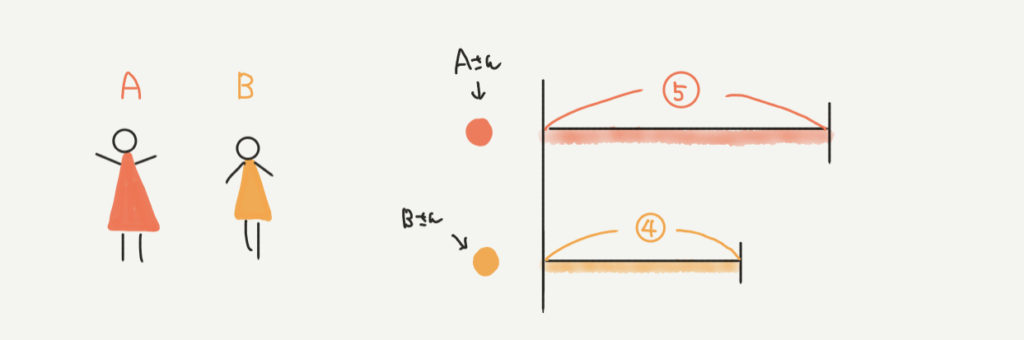
まずは①の図をかいてみましょう!
AさんとBさんの所持金を線分図に直すだけなので、そこまでむずかしくはなかったと思います。
できなかった受験生はまず上の図をきちんとかけるように練習しましょう。
②の線分図
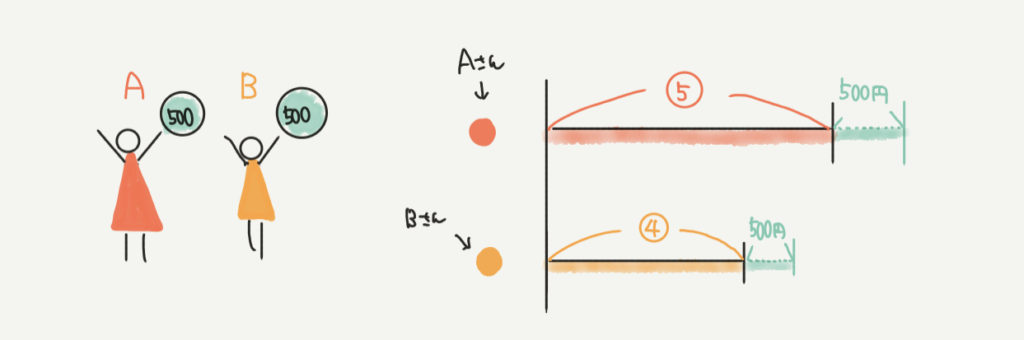
2人とも500円もらったので、2人の線分図に500円を足していきます。
緑色の部分が追加で書いた部分です。
ここまでも大丈夫ですか??
まだそこまでむずかしくないと思います!
しっかりついてきてくださいね〜!
③の線分図
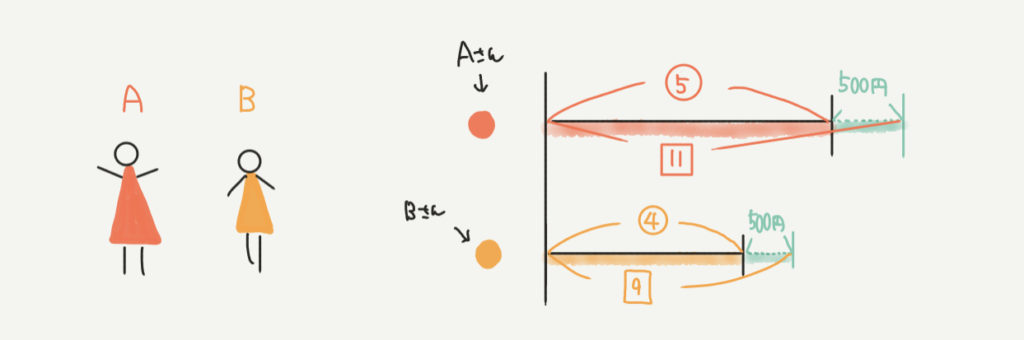
するとお金をもらった後の2人の所持金の比は11:9なので、それを書き足していきます。
どこからどこまでが□の11で、どこからどこまでが□の9なのかを間違えないようにしましょう!
算数を得意にするコツ、なんで記号を同じにしてはいけないの?
兄弟の所持金の変化から2人の持っていた金額を求めるには?

 わかみや先生
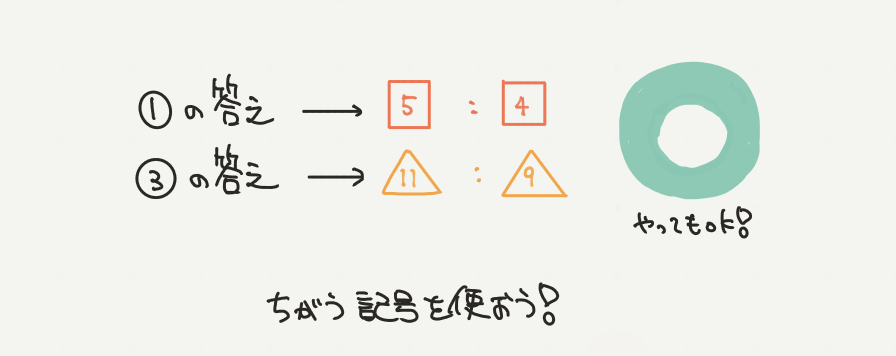
わかみや先生さっきの①、③問題で、比の記号を①と③で同じにかいてしまった受験生はいますか?
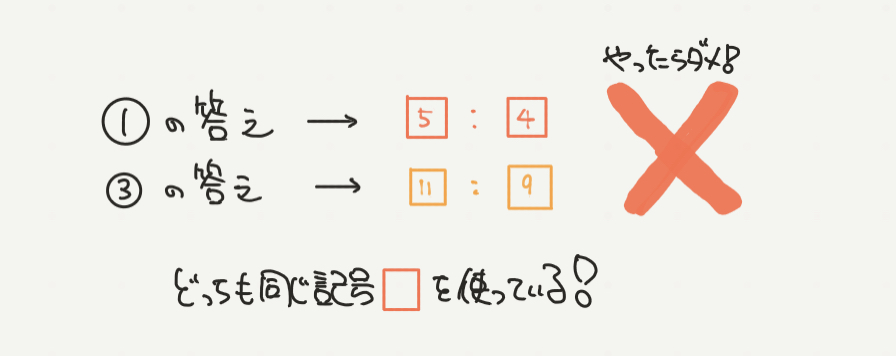

もし、記号をどちらも同じにしてしまっていたら、それは危険です!
せっかくがんばっているのに不正解になってしまう可能性がありますので注意しましょう。

それでは問題にチャレンジです!
問題に挑戦!
解答
答えを見るにはここをクリック!
200円
この記事を書いている人はこんな人




解説を読んで「 割合と比 」を攻略しよう!

STEP1:問題文を線分図にしよう
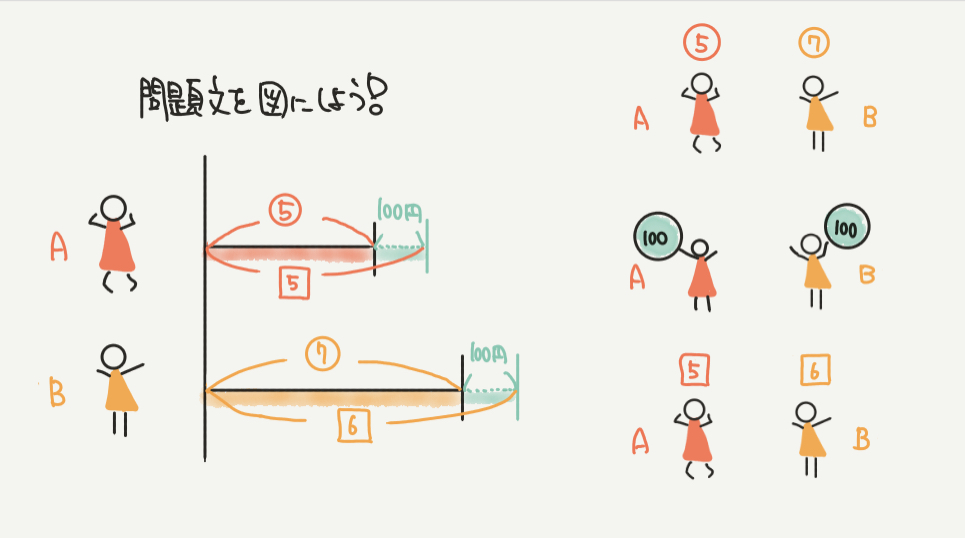

まずはいつも通り!問題文の内容を図にしていきましょう。
例題通りに書くと、上の図のように書くことができますね!
ちなみに絵でかくと右のようになります。
さあ、どんどんいきますよ!
STEP2:同じところがない!なら作ろう!!
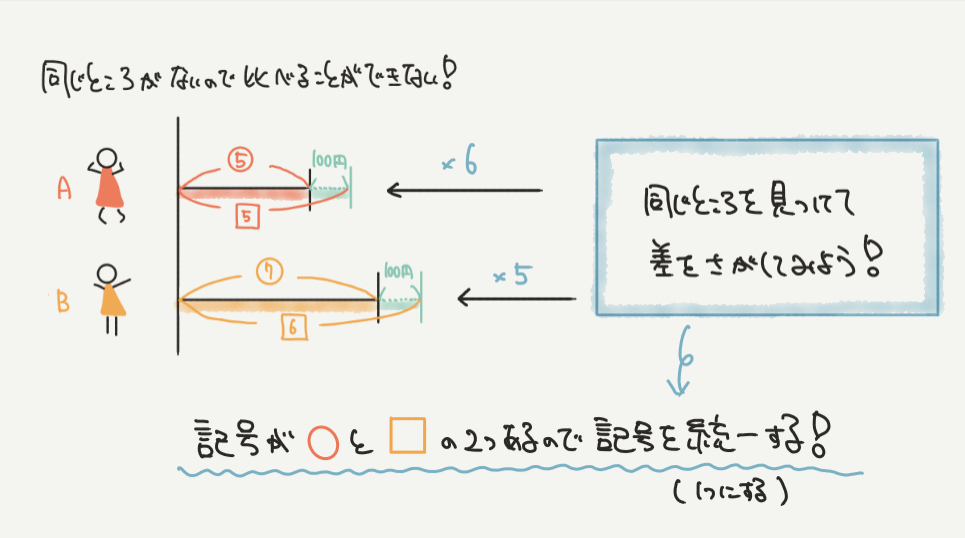

線分図をSTEP1のように書いたら、今度は同じところをさがしましょう。
ただ、このままさがしても同じところは見つけられません。
そういうときは、同じところを作っていきましょう。
この問題では記号が○と□で2種類あるので、記号を統一して、記号を2つから1つにしていきましょう!
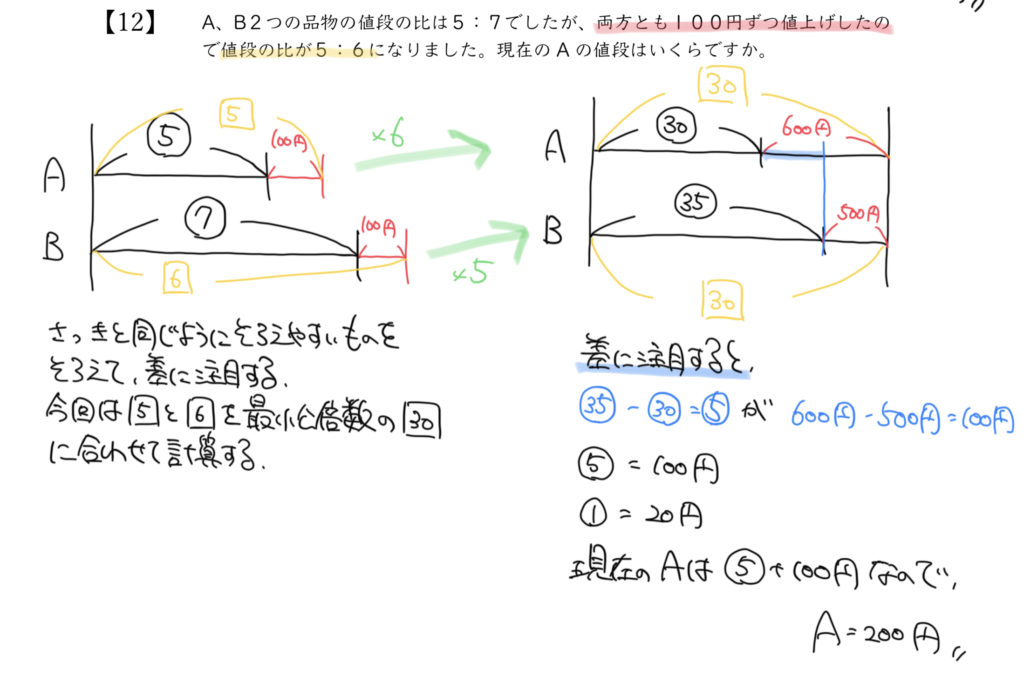
今回は、Aを6倍、Bを5倍すれば同じ記号(□の30)を作ることができます!
Aの線分図を6倍→□の5×6倍=□の30
Bの線分図を5倍→□の6×5倍=□の30
STEP3:同じところを作る
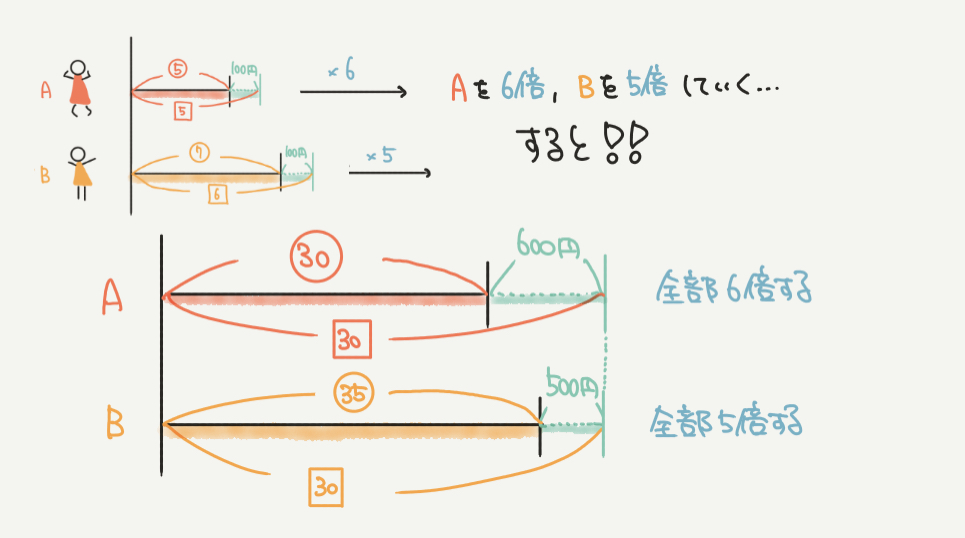

AとBをそれぞれ6倍、5倍すると上の図のようになりますね。
気をつけてほしいのは、Aの線分図全部を6倍するので、⑤も100円もしっかり6倍していきましょう。
⑤×6=㉚
100円×6=600円、とわかりますね!
ここまでかければ、最後に差を見つけて答えを出していくだけです!!
STEP4:同じところから差を見つけて解いていきましょう
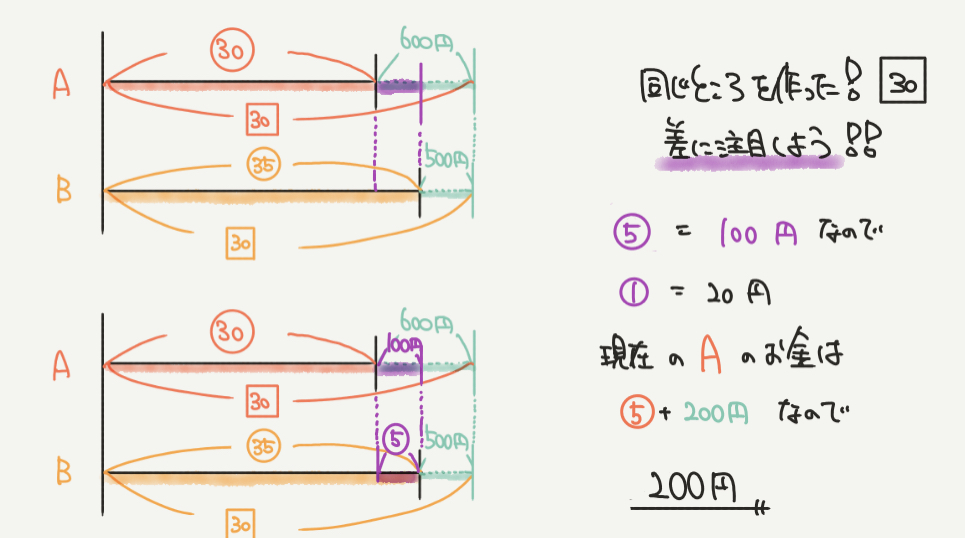

最後は線分図から見つけられる差に注目していきましょう。
ちなみに線分図を書くときは、どこからどこまでが同じなのかを忘れずに書いてくださいね。
注目してほしい差は紫色の部分です。
600円–500円=100円が差になります。
同じ部分の差が㉟–㉚=⑤、と表せるので
⑤=100円となり、
①=20円と求めることができます。
よって現在のAのお金(⑤+100円)は200円と分かります。
品物2つの比の変化から値段を求める問題のまとめ
今回の問題で大事なポイント
線分図の書き方(STEP1)
・問題文をきちんと図にする練習をしよう
「同じところを見つける、作る」考え方(STEP2)
・同じところを今回は作ろう!(STEP3)
以上が今日の問題でした!いかがでしたでしょうか?
線分図を間違えないようにかければ、かんたんに正解できたと思います。
逆に、できなかった受験生はこの線分図をうまく書けないことが多いのできちんと確認するようにしましょう。
同じものを作るとき、基本的には合わせたい数の最小公倍数にそろえるのが基本です。
(今回で言うと、6と5の最小公倍数の□の30に合わせることが大事でした。)
ちなみに今回の最小公倍数は、
○の5と7の最小公倍数か、□の5と6の最小公倍数の2つがあったのでどちらでそろえても答えは出ますが、□の5と6の方が合わせやすかったので30でそろえました。
記号をしっかりと使い分ける練習もこれからより大事になってきます。
記号の使い分けは、何を基準に記号を書くかが重要ですので、
この問題やはじめにで紹介した復習問題をしっかりと解き直しておくようにしておきましょう!