【中学受験攻略】地点間の最短経路を求める問題で場合の数を勉強しよう！

はじめに

今日は「 場合の数 」の問題にチャレンジです。
「 場合の数 」の問題も気づいたらあっという間に7問目！
これまでの問題を解きたい受験生は下の記事をクリックしてみてください！

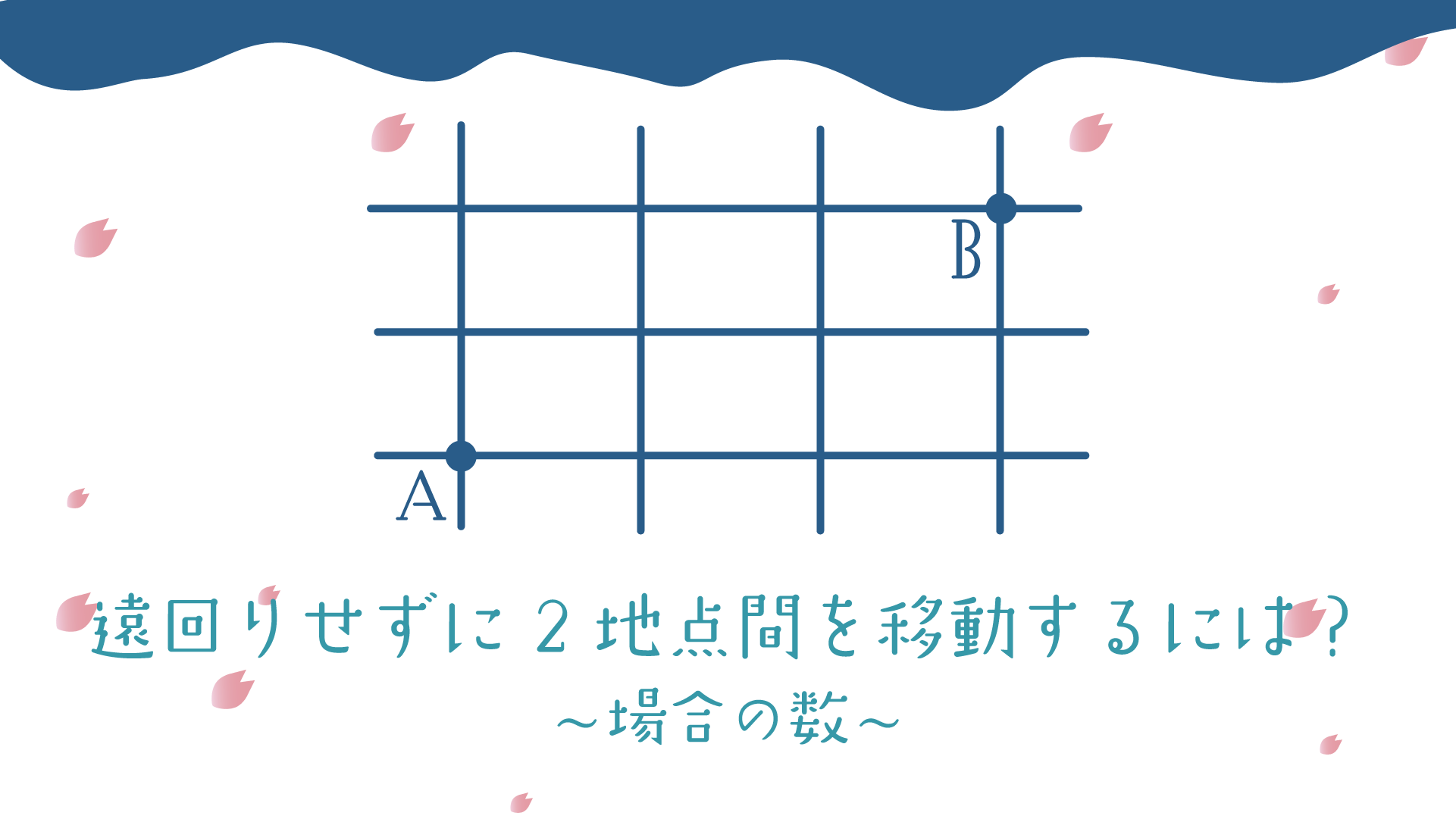
最短で行く場合の数はこう考えよう！

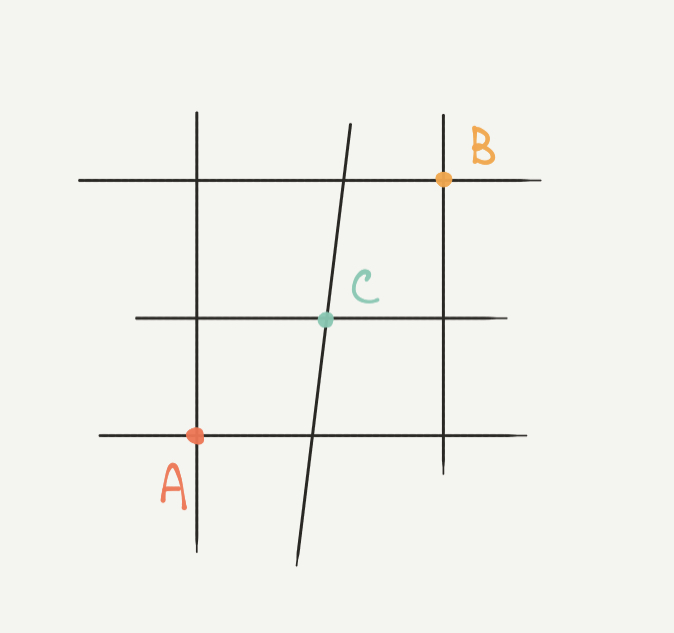
たとえば、点A、点B、点Cがあったとします。
このとき、点Aから点Bへ最短で進む場合の数を求めてみましょう。

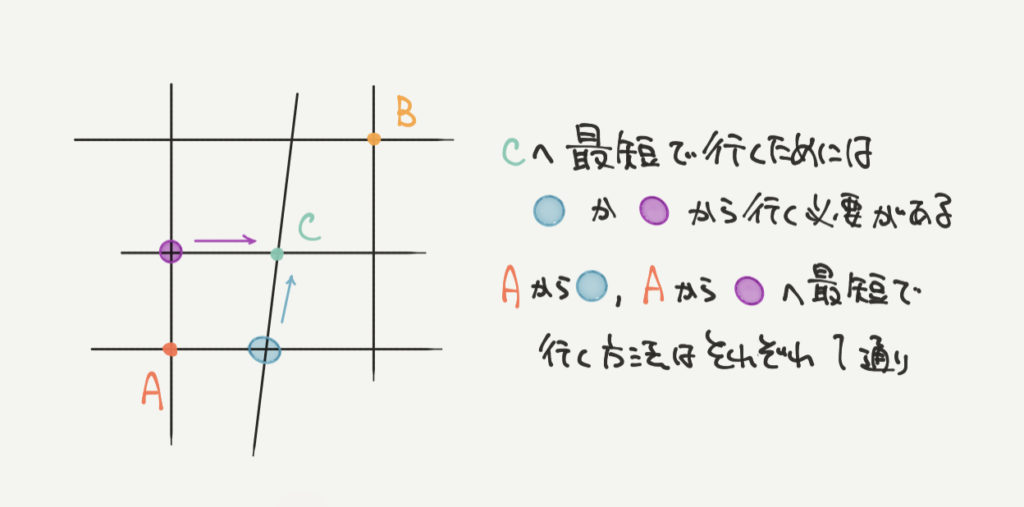
点Aから点Cへ最短距離きょりで進むためには、●か●を通る必要があります。
なので、点Aから●と点Aから●へ最短でいく場合の数を書き出してみましょう。
すると、最短で点Aから●への進み方は1通り、Aから●への進み方も1通りとなります。

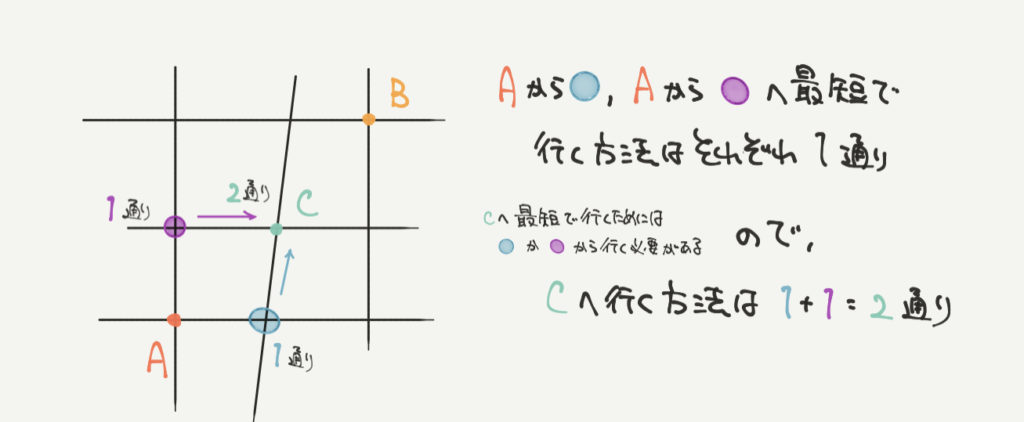
つまり点Cへ行くためには点Aから●への進み方は1通りのパターンと、
Aから●への進み方の1通りのパターンの合計2通りの方法があります。

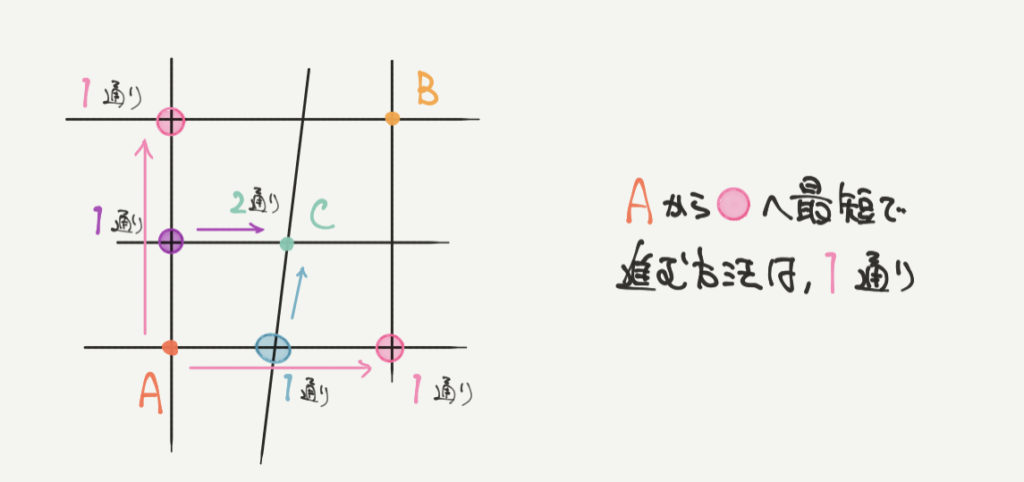
同じように●へ最短で進むときの場合の数を求めます。
点Aから●へ最短で進むときの方法はそれぞれ1通りです。
なので、図に1通りと書くことができます。

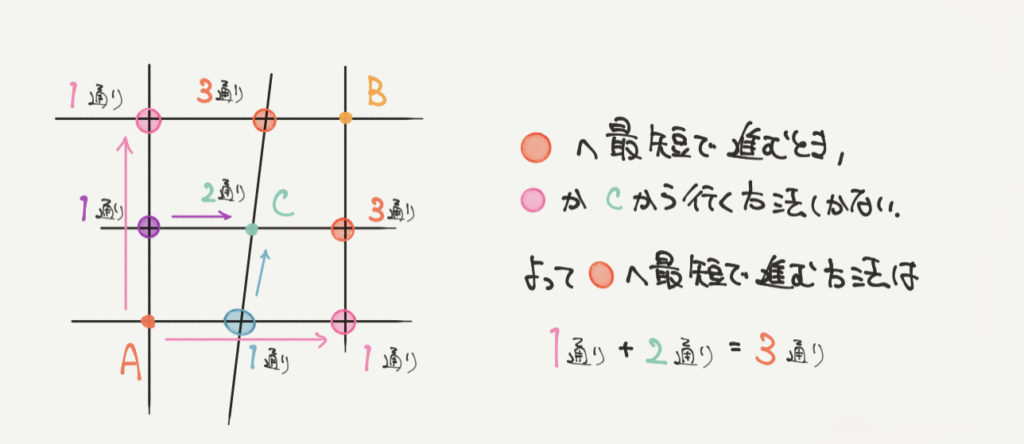
点Aから●へ最短の道が1通りとなりますので、
次に●への行き方を考えてみましょう。
点Aから●への最短の道は直前で点Cか●にいる必要があります。

よって、●への最短の道＝点Cへの道の数＋●への道の数となります。
1通り＋2通り＝3通りとなります。

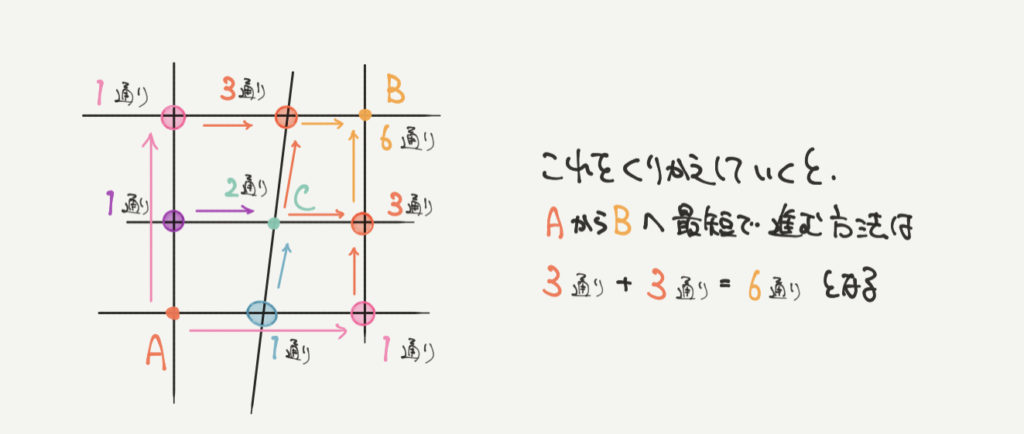
このように求めたい場所への道順を求めるには、
その直前までいるはずの場所への場合の数を足し算すればいいということがわかりますね。
点Bへの最短の道では、直前で●と●にいる必要がありますので
3通り＋3通り＝6通りが正解になります。

「 場合の数 」の問題に挑戦ちょうせん！

下の図のように、東西に5本、南北に6本の道路が直角に交わっています。
この道路を通って、A地点から遠回りせずにB地点へ行きます。これについて次の問いに答えなさい。

① 行く方法は全部で何通りありますか。
② Cを通らずに行く方法は何通りありますか。

解答

この記事を書いている人はこんな人

解説を読んで「 場合の数 」を攻略こうりゃくしよう！

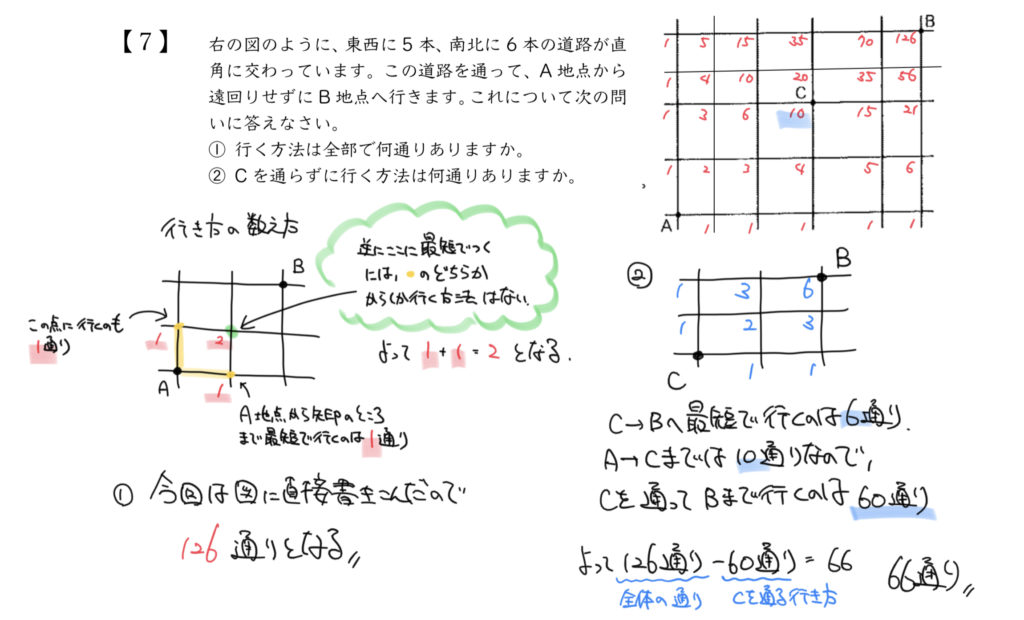
STEP1：最短の道を書きこんでいこう！

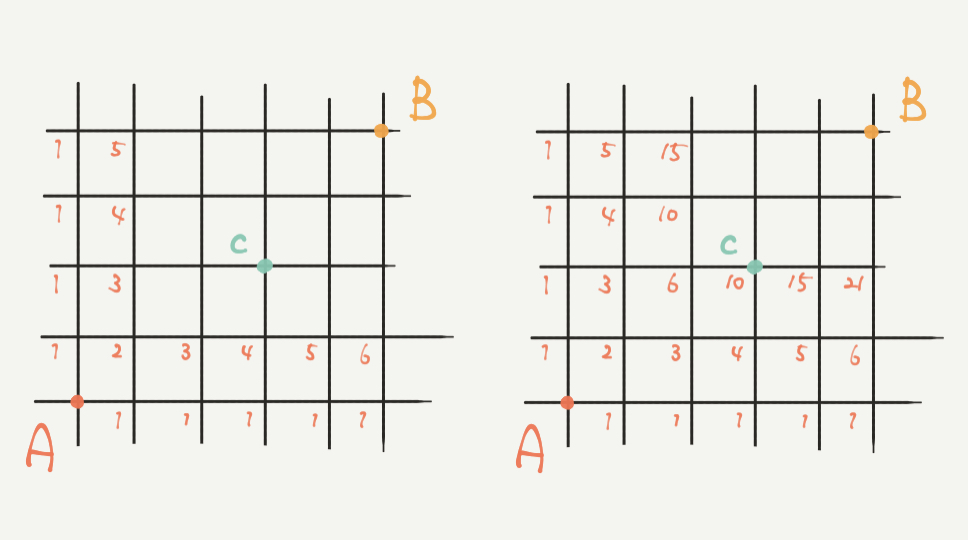
まずはヒントに書いたようにそれぞれの点への最短ルートの場合の数を書きこんでいきましょう。
①の問題はひたすら書きこんで足し算していくだけですので、特に解説はありません！
図を見ながらみなさんも計算してみて下さい。

STEP2：足し算していくと126通りとなる

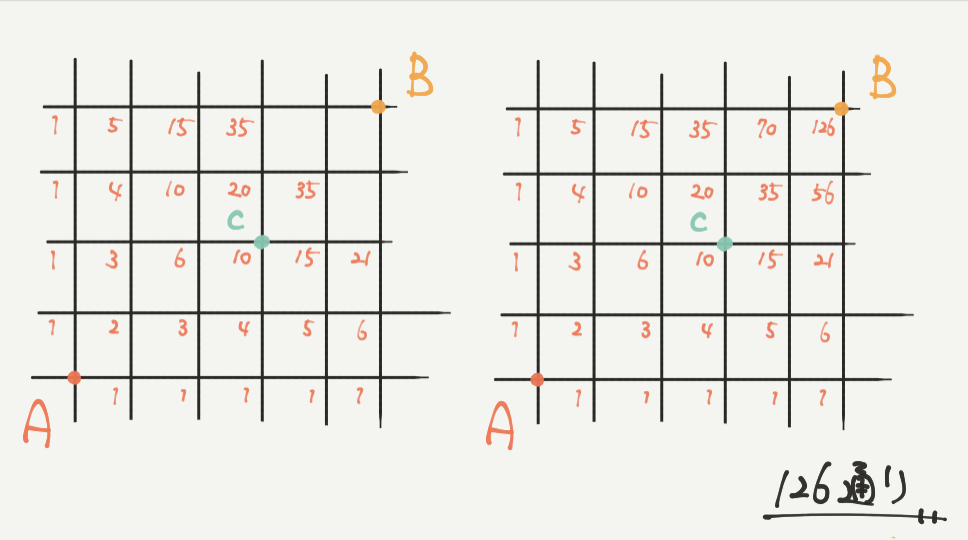
先ほどの考えを理解すれば、図に全部書き込むことができます。

STEP3：Cを通らずにAからBへ向かうときの場合の数を求めよう

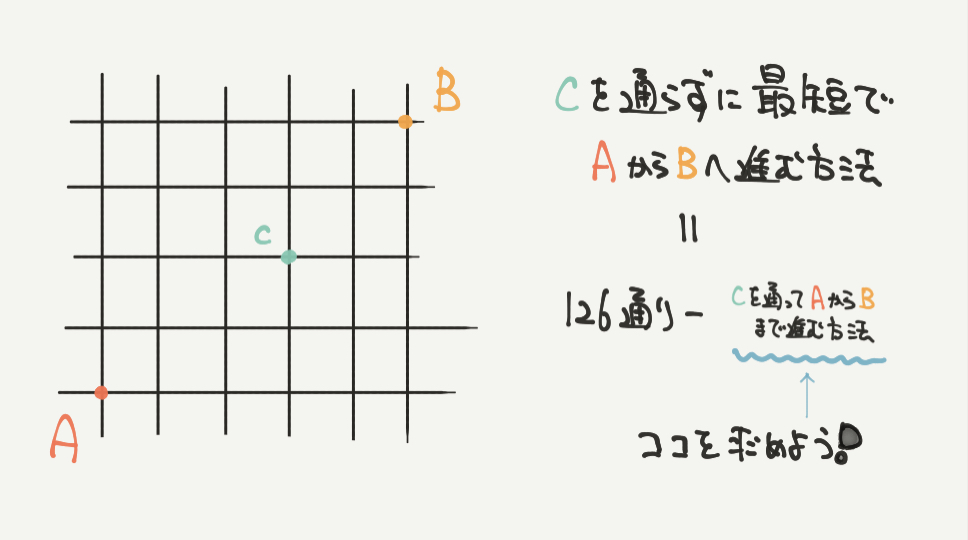
Cを通らずに最短でAからBへ向かうときの場合の数は、
全体（126通り）-Cを通ってAからBへ向かうときの場合の数、となります。
なのでCを通ってAからBへ向かうときの場合の数を計算しましょう。

STEP4：AからCまでが10通り、CからBまでが6通り

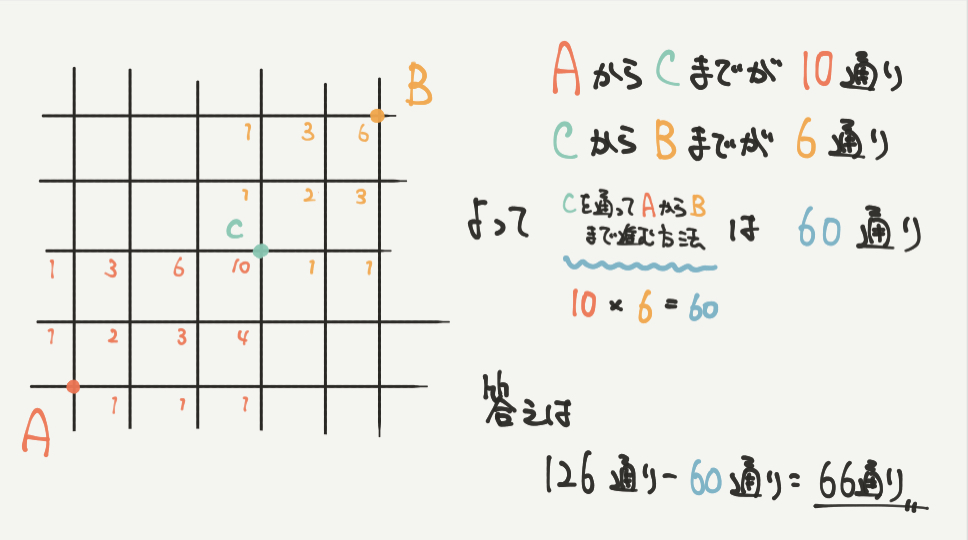
AからCまでの行き方はSTEP1で求めた通り、10通りです。

CからBへの行き方はまた1から数える必要があります。
点Cをスタート地点にBまで進むときの場合の数を求めると、図から6通りとなります。
よって、Cを通ってAからBへ向かうときの場合の数は10通り×6通り＝60通り

答えは126通り-60通り＝66通りとなります。

遠回りせずに2地点間を移動する場合の数を求める問題のまとめ

「 場合の数 」の問題で大事なポイント

「最短の道で進むとき 」の考え方
・直前の場所の行き方を足し算して求めましょう！
・困ったらかんたんな例を使いながら計算してみましょう

以上で今日の問題は終わりです！
最後まで読んでくれてありがとうございました！！
次の問題で会いましょう！！！

その他の単元の問題の復習はこちらから！