はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います!
今回もSPIの「確率」の勉強です。
前回までの基礎編に引き続き今回は応用編です。
正直SPIという時間との戦いの試験で「確率」の応用を完璧に解くことは難しいと思います。
場合によってはこの難易度の問題は戦略的に飛ばしてもいいくらいだと思います。
しかしそんな鬼畜問題にチャレンジしたいという勇気ある就活生の皆さんのために
私も頑張って解説を書いてまいりたいと思います!
頑張っていきましょう。
この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
[98]問題に挑戦!
答えを見るにはここをクリック!
14/25
[98]解説を見てみよう!
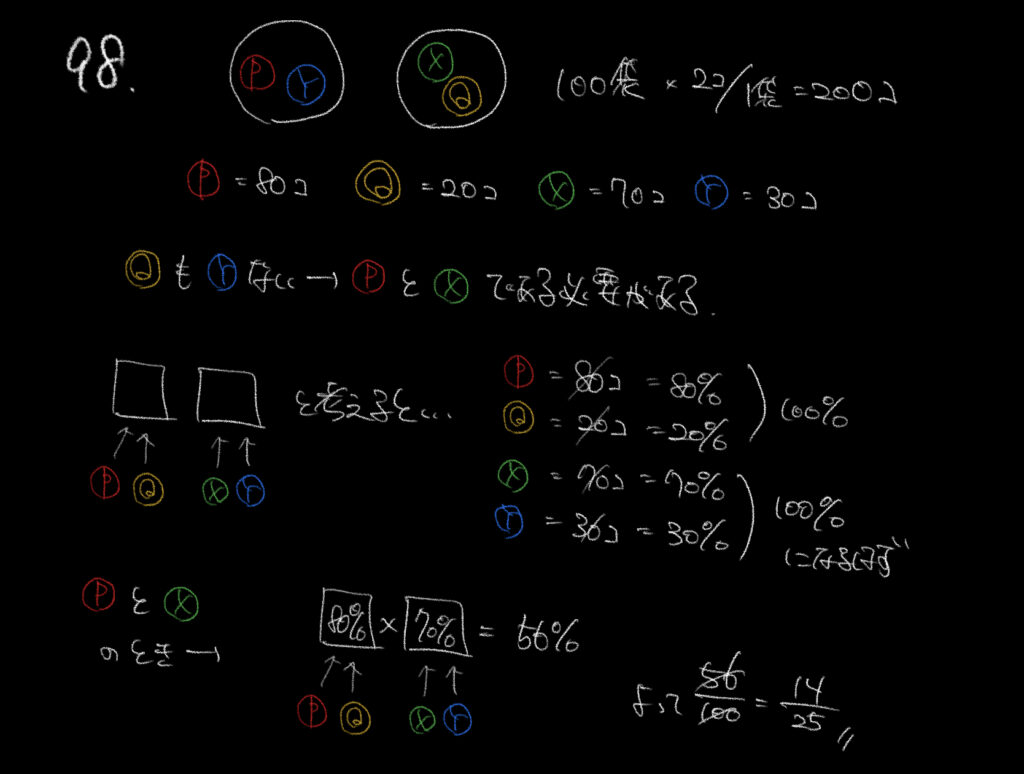
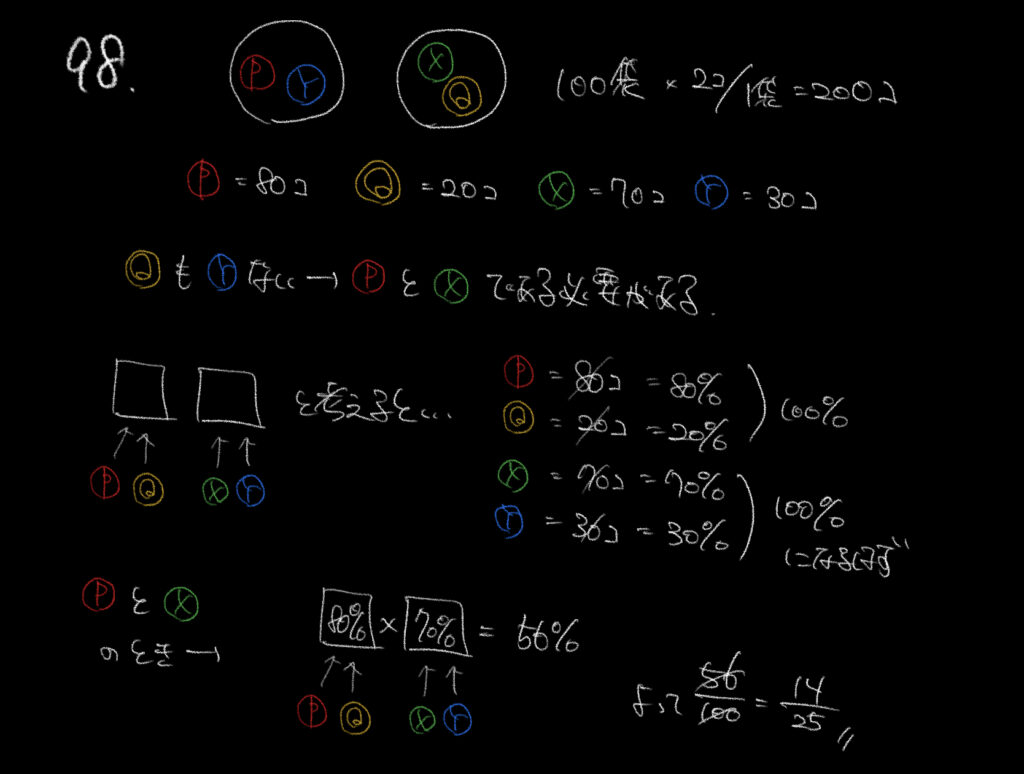



確率の応用です!ここはSPI最難関といっても過言ではありません。
かなり難しいですが、わかりやすく丁寧に頑張ります。
一緒に頑張っていきましょう。
4つの文字を色分けして考えましょう。
“商品QもYも入っていない確率”ということは商品PとXが入っているということです。
商品がPかQである確率は個数の比率からそれぞれ80%、20%です。
商品XかYが入っている確率はそれぞれ70%、30%です。
なのではじめにP、次にXと考えると、80%×70%=56%(14/25)です。
これが応用の中でも簡単な問題です。
あっやばい、と思った方はこちらの基礎編からまず攻略していきましょう!


[99]問題に挑戦!
答えを見るにはここをクリック!
①1/5
②4/5
③4/9
④8/27
[99]解説を見てみよう!
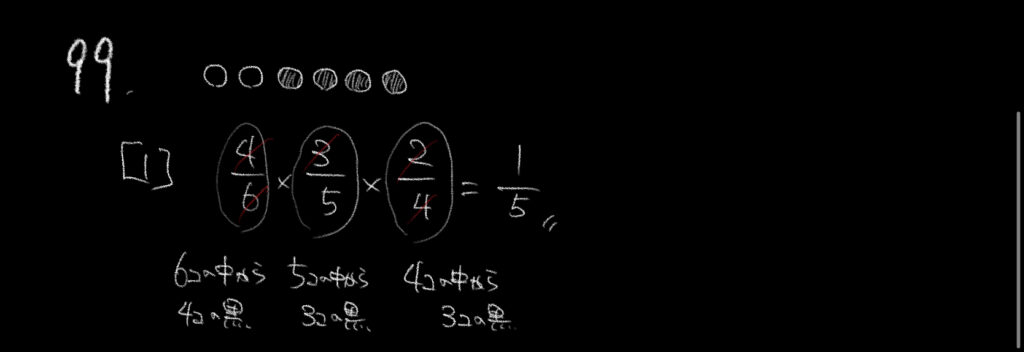
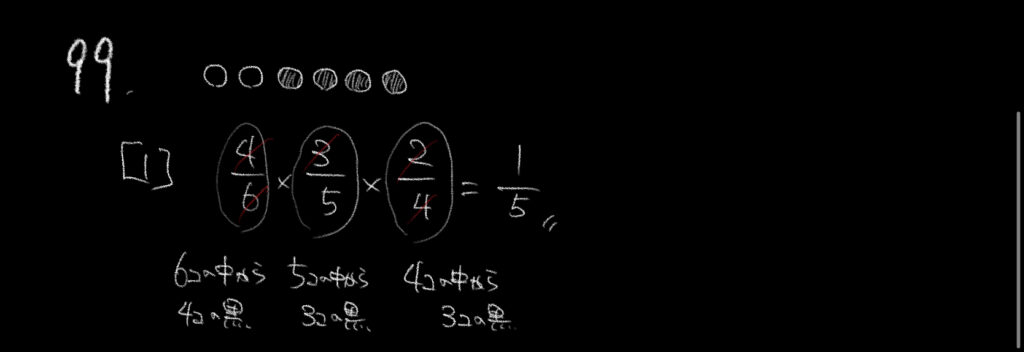
①黒が3連続なので、順番に考えると
6個の中から4個の黒、
5個の中から3個の黒、
4個の中から2個の黒を取り出せばいいので
4/6×3/5×2/4=1/5となります。


②黒の碁石が2個以上のとき=黒の碁石が2個、黒の碁石が3個のときです。
①で黒が3連続で出る確率を求めたので、今度は黒い碁石が2個出る確率を求めていきましょう。
はじめに白が出た場合を考えると、
6個の中から2個の白、
5個の中から4個の黒、
4個の中から3個の黒となり、
2/6×4/5×3/4=1/5となります。
同様に2回目に白が出るとき、3回目に白が出るときと3パターンがあるので
1/5×3=3/5となります。
よって①の答え(黒い碁石が3個になる確率=1/5)と足して4/5とわかります。
③②と同様に考えます。ただし今回は出した石を元に戻して行います。これに気をつけましょう。
はじめに白が出たときのことを考えると、
6個の中から2個の白、その後石を戻すので
次の6個の中から4個の黒、またまた石を戻して
次の6個の中からも4個の黒となり、
2/6×4/6×4/6=4/27となります。
先ほどと同様にはじめに出た時、2回目、3回目と3パターンあるので
4/27×3=4/9になります。
④今回難しかったのはこちらの問題でした。
4度目に3回目の黒が出る、ということは、
3度目までに2回黒が出ているはずです。
3回の間に2回黒を出す確率は③で求めているので、4/9とわかります。
4回目に黒い石を出す確率は4個/6個なので、4/6となり、
よって求めたい確率が4/9×4/6=8/27と計算できます!
[100]問題に挑戦!
答えを見るにはここをクリック!
①1/7
②1/28
[100]解説を見てみよう!
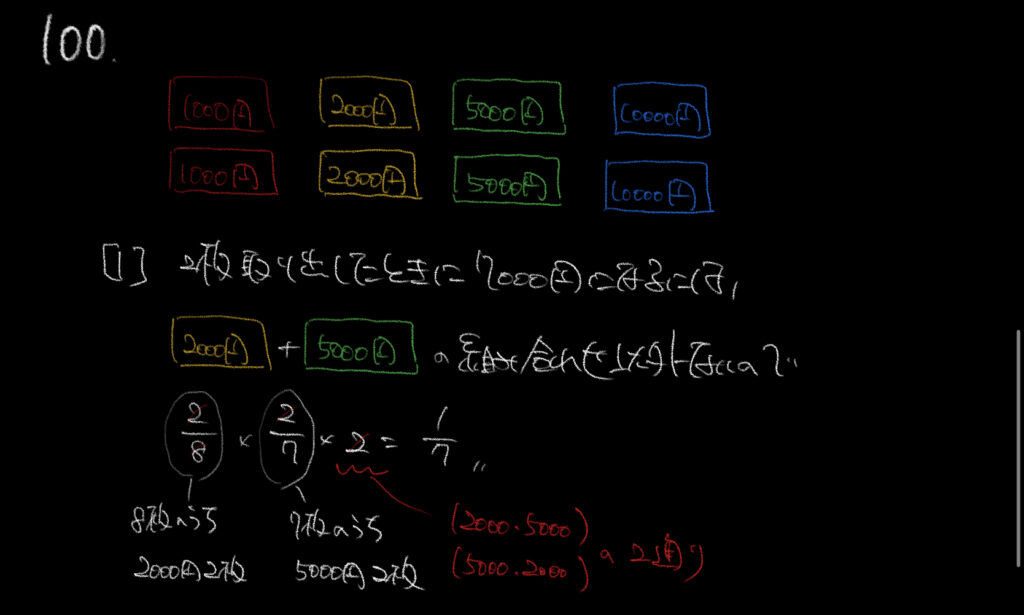
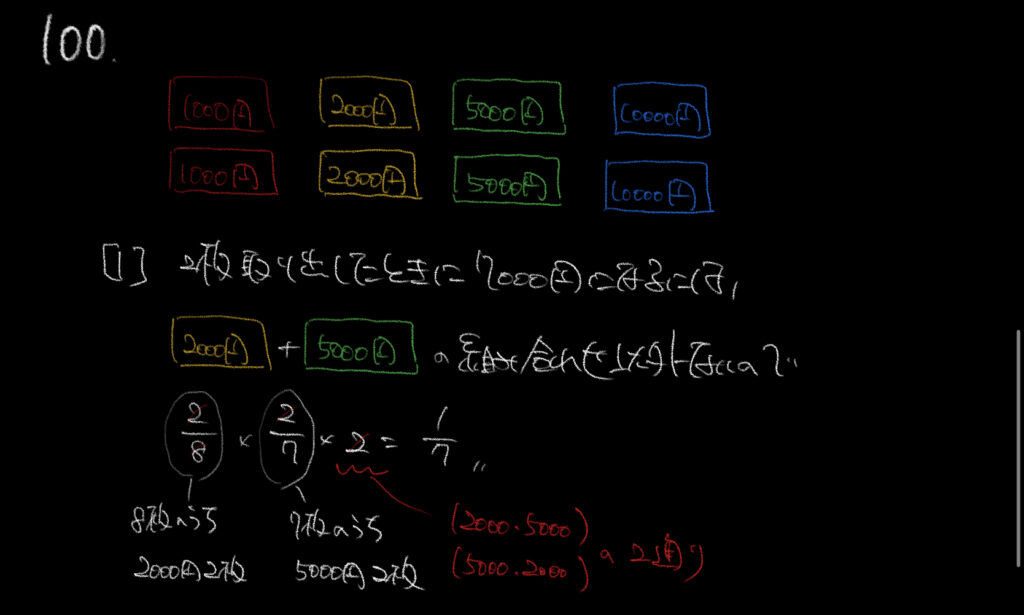
①この確率の問題は簡単です!安心してください。
今回簡単だといった理由は、7000円になる組み合わせが1通りしかないからです!
7000円を作れる組み合わせは2000円+5000円のみとなります。
よって2000円、5000円を引く確率を求めます。
ここで気をつけて欲しいのがいつものように、順番を考えてあげることです。
7000円になる組み合わせは2000円、5000円ですが、
7000円を引く順番は(2000-5000)か(5000-2000)の2通りあります。
あとは計算して求めましょう!
5000円と2000円はそれぞれ2枚あるので、
8枚中2枚の5000円と7枚中2枚の2000円の確率を求めて、順番を考慮して2倍してあげましょう!
2/8×2/7×2=1/7
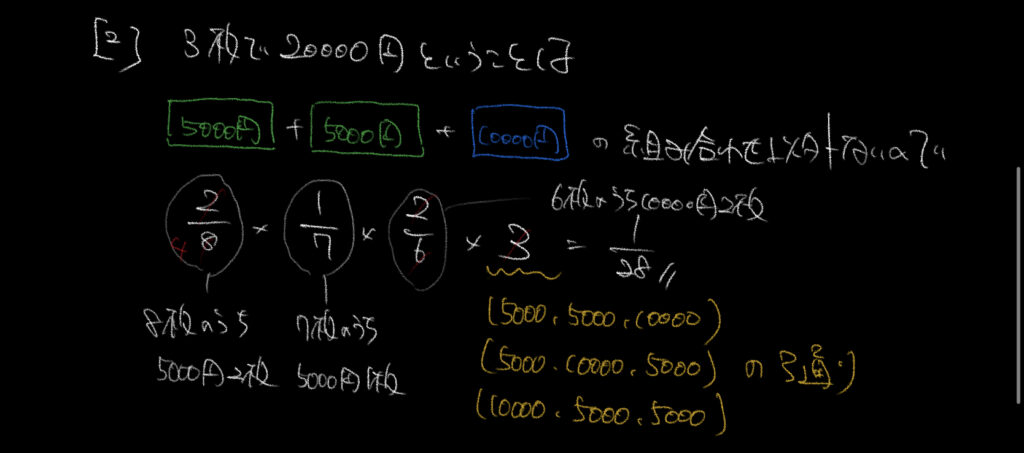
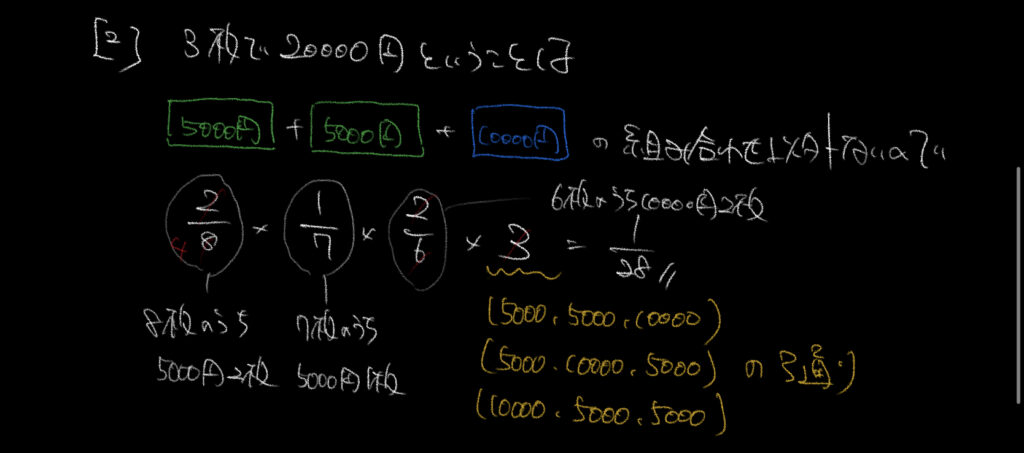
②①とほぼ一緒です!
組み合わせは5000-5000-10000ですが順番は3通りあります。
そこに気をつけて計算しましょう。
解説では5000-5000-10000の順番で解いています。
最初に5000円を引く確率:8枚中2枚
次に5000円を引く確率:7枚中1枚
最後に10000円を引く確率:6枚中2枚
この確率が1/84なのでこれを3倍した1/28が答えになります!

[101]問題に挑戦!
答えを見るにはここをクリック!
①4/7
②4/7
[101]解説を見てみよう!
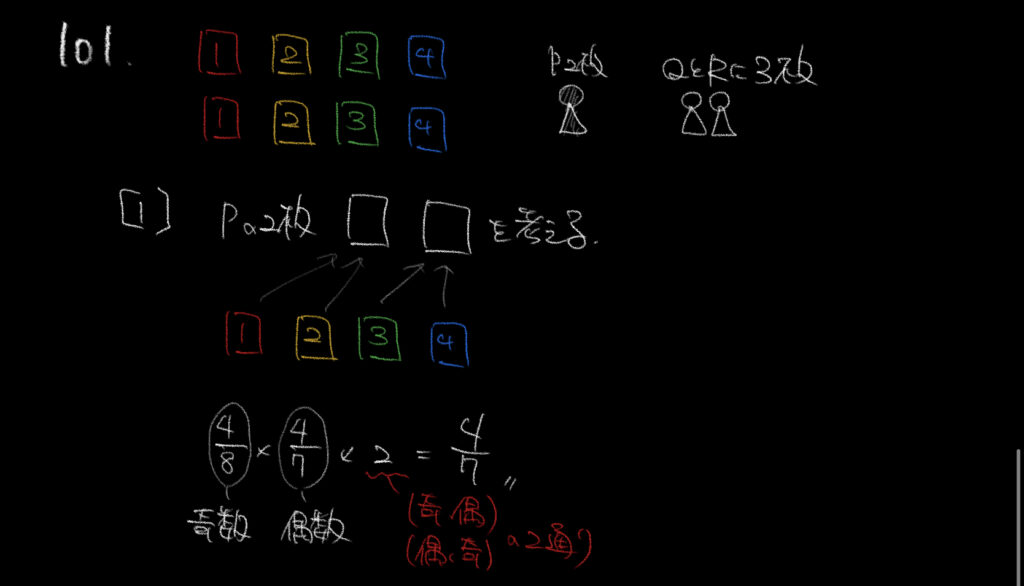
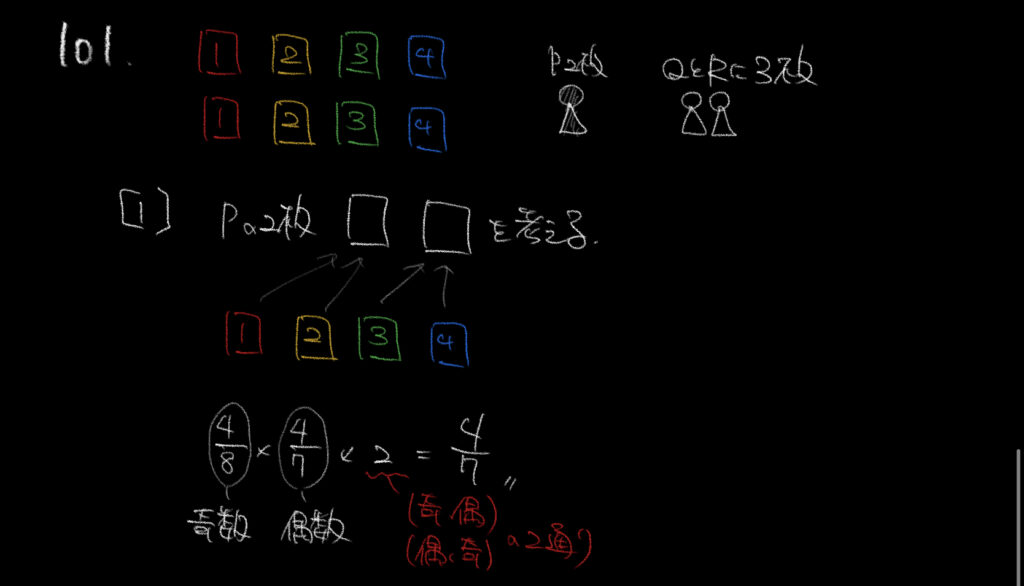
①1からしっかり確率を解いている方ならそろそろこの問題が簡単に見えてくる頃ではないでしょうか?
奇数、偶数を1枚ずつ引く場合の組み合わせは、(奇数-偶数)(偶数-奇数)の2パターンあります。
はじめに奇数、その次に偶数だったときを考えます。
8枚中奇数は4枚あるので、4/8。
次に7枚中偶数も4枚あるので4/7。
この順番が2通りあるので2倍して、
4/8×4/7×2=4/7と求めることができます!


②余事象を使って考えましょう。
(余事象でなくても解けますが、今回は余事象を使った解説をしていきます。)
今回、考えられるQのカードの種類は1種類、2種類か3種類かのパターンしかありません。
よって、全体–Qに配られるカードが異なる2つの数字のときの確率–Qに配られるカードが全部同じときの確率=Qに配られるカードが異なる3つの数字になる確率となります。
これを計算することで答えを出すことができます。
Qに配られるカードが異なる2つの数字のときの確率と全部同じのときの確率を同時に求めていきます。
メモの緑の部分で、2つの同じカードを引く確率を求め、3倍します。
この3倍は解説にも書いてある通り、同じカードを2回引くときの順番を表しています。
最後の4倍はその同じだったカードに書かれている数字が1、2、3、4のいずれか4パターンのときです。
これを計算すると3/7となり、
1−3/7=4/7と求めることができます。


[102]問題に挑戦!
答えを見るにはここをクリック!
①12%
②70.56%
[102]解説を見てみよう!


①比率というのが難しいポイントだったかもしれません。
解説では比率を○で表しています。
今回は赤玉と白玉が3:2の比率で入っているので③と②と表します。
この中のあたりの割合がそれぞれ20%と10%なので、○で表すことができます。
赤玉の当たり:③×0.2(20%)
白玉の当たり:②×0.1(10%)
全体⑤のうち、当たりの赤玉は○の0.6なので0.6/5=12%となります。


②①で仮定したように全体⑤に対して、ハズレくじは○の4.2あります。
赤玉の当たり:③×0.2(20%)
白玉の当たり:②×0.1(10%)
ここからハズレのくじを計算できますね!
よって2連続でハズレを引く確率は
4.2/5×4.2/5=17.64/25
17.64/25=70.56%となり71%と求められます。
仮定して考えることが重要な問題でした。


[103]問題に挑戦!
答えを見るにはここをクリック!
①15/64
②39/64
[103]解説を見てみよう!


①私はめんどくさいやり方でやってしまったので、別解を参考にしてください。
(後で思いついて泣きそうになりました。)
余事象で解く方がはるかに楽です。解説の分量からもよくわかると思います。
要は全体からPがグーで勝つ確率を引けばいいのです。
Pがグーで勝ってしまうとき、Pは1/2の確率でグーを出します。
そしてQは負けるので1/4のチョキを出してしまいます。
よってPがグーで勝つ確率が1/8とわかったので、全体(1)から1/8を引いた7/8が答えとなります!


②こちらも余事象で考えましょう。
本当に便利ですよね余事象(いまさら)
解説をさらにわかりやすく書いたものがこちらです。
全体からPが2回ともチョキかパーで勝つかあいこにならない確率を引きます。
Pがチョキで勝つ確率:1/4×1/2=1/8
Pがパーで勝つ確率:1/4×1/4=1/16
Pがチョキであいこになる確率:1/4×1/4=1/16
Pがパーであいこになる確率:1/4×1/2=1/8
1/8+1/16+1/16+1/8=3/8
チョキかパーで勝つかあいこにならない確率=1-3/8なので5/8
チョキかパーで勝つかあいこにならない確率が5/8とわかります。
よってそれが2回連続で起きる可能性は25/64。
全体からPが2回ともチョキかパーで勝つかあいこにならない確率が答えなので、
正解は全体(1)から25/64を引いた39/64となります!!


まとめ
いかがでしたでしょうか?
SPIで出題される問題の難易度でいえば間違いなく上位に入るくらいの鬼畜さです。
正直テストでこれが出たら素直に諦めて次に行ったほうがいいです。
これ以上の難易度の問題は出ないはずなので、
完璧にマスターしたい!確率を武器にしたいと思っている方はしっかり復習しておいてください!
次からは割合の単元になります。
割合は中学受験でも出ている内容なのでそこに着さされている攻略法をおさえて解くといいでしょう!








