【SPI試験徹底対策】円順列、重複の問題攻略法を解説！仕切りの考え方を活用せよ！（全５問）

2023年11月28日

はじめに

わかみや先生

みなさん、こんにちは！「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います！

SPIで出題される問題の中で個人的に最も難しいと思うのが
この円順列や重複に関する問題だと思います。

全5問の今回の問題で大切になってくるのが「仕切りの考え」です。
これは前の記事でも取り扱った「ボックスの考え」の応用になりますので、
気になる方は先にこちらの記事から見ていただけると良いかと思います！

［82］問題に挑戦！

［82］リンゴ３個、ミカン３個、カキ２個がある。ただし、リンゴ、ミカン、カキの中で区別はないものとする。
①ここから４個取り出したい。選び方は何通りか。
②ここから５個取り出したい。選び方は何通りあるか。ただし、各種最低１個は選ぶものとする。
③全部を横一列に並べたい。並べ方は何通りあるか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

①10通り
②5通り
③560通り

［82］解説を見てみよう！

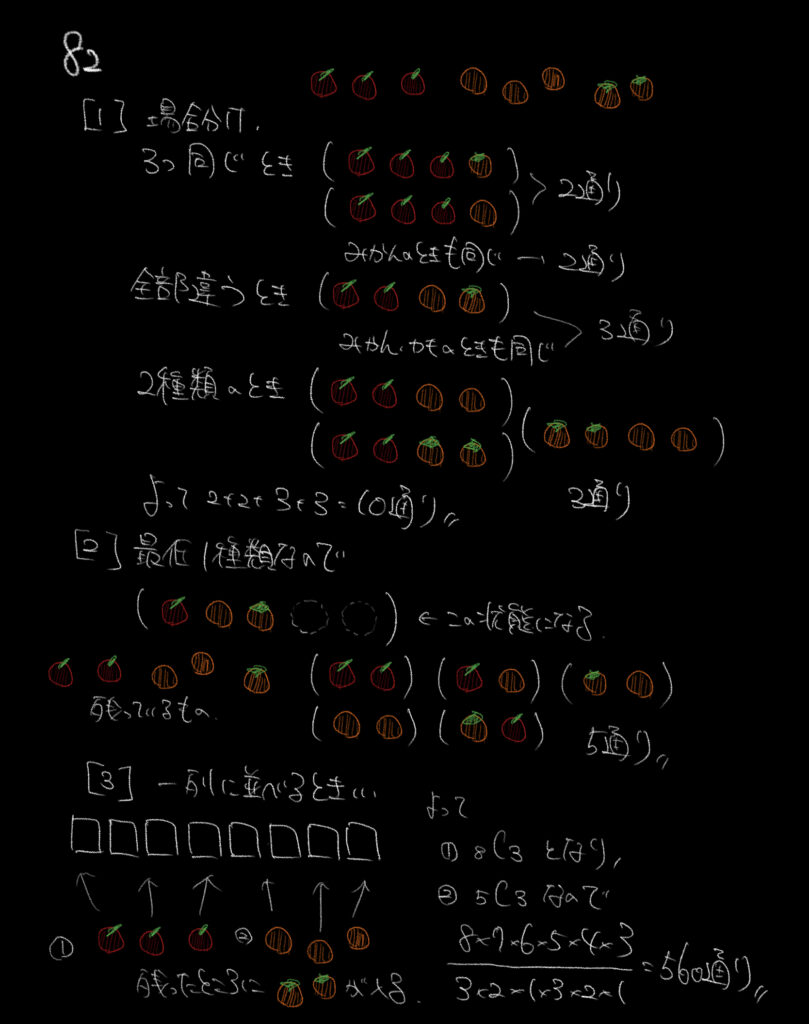
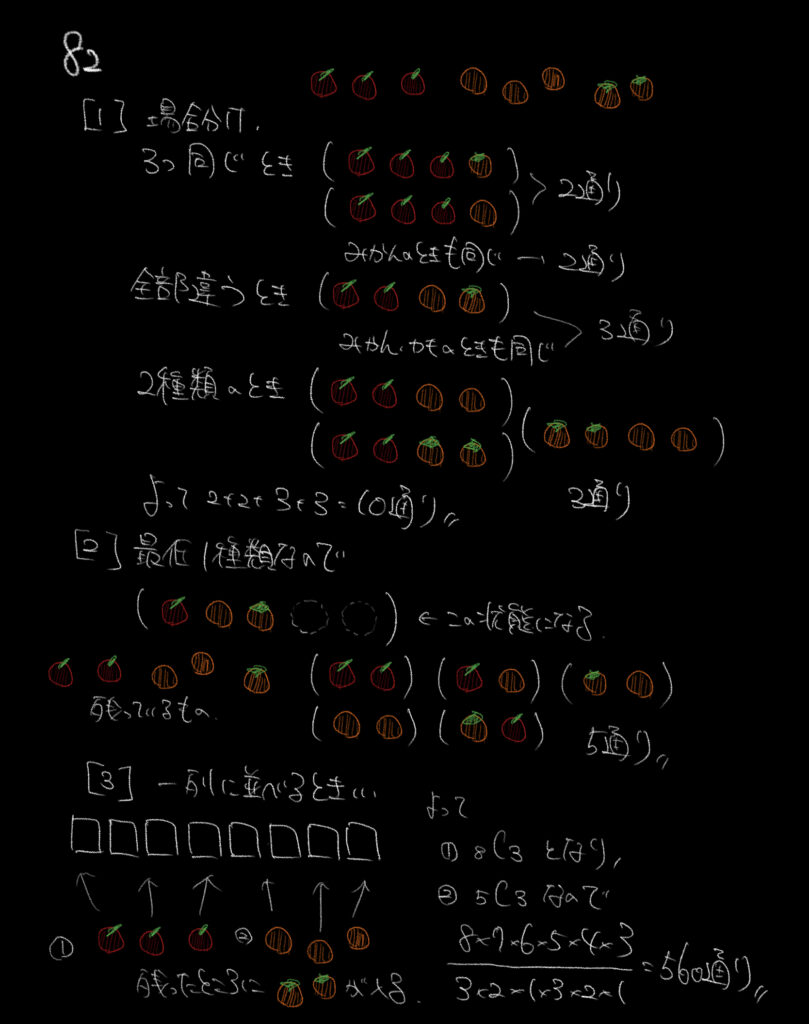
タイトルにある仕切りの考えは一回置いておいて、
まずは自力で場合わけして解いていきましょう。気合です！

①SPIの問題で場合分けをするときのコツは少ない方から数えていく、ということです。
この問題の場合、３つ同じときと３つ全て異なるときが少ないとなんとなくわかると思います。

３つ同じとき：りんご３つ＋カキ、りんご３つ＋みかん、みかん３つ＋りんご、みかん３つ＋カキ
全部違うとき：りんご２つ＋カキ＋みかん、みかん２つ＋カキ＋りんご、カキ２つ＋りんご＋みかん
２種類のとき：りんご２つ＋みかん２つ、みかん２つ＋カキ２つ、カキ２つ＋りんご２つ

めんどくさいのを最後に置いておいて、計算しましょう。
解説ではスペースの関係で絵が描かれていませんが、
みかんのとき、カキのときも考えてあげましょう！
全部の場合の数を足し合わせて10通りとなります。

②最低1種類は選ぶ系の問題は実はめちゃめちゃ簡単です。
全て一個とってくれるので、５個選ぶ問題でも実際に考えないといけないのは２つ分のみ。
残っているりんご、みかん、カキの数に注意して求めていきましょう。

③最後は「ボックスの考え」と、PとCの復習が必要な問題でした。
１からやっている方はもう見慣れてしまっていると思いますが、
ボックスとは場合分けの時に使われる解法のことです。

今回８個のフルーツを並べる、またそれぞれの果実は区別しないと書いてあるので、
組み合わせの公式を使って解いていきます。

まず８個の中から、りんごを３つ入れます。
そして余った５個の中から、みかんを入れる３箇所を入れて、
最後に残った部分にカキを入れます。

これを計算すると、8C3×5C3になり560通りと求められます。

（8C3：８個の中からりんごを３つ入れる）
（5C3：余った５個の中からみかんを３箇所入れる）

［83］問題に挑戦！

［83］10円、20円、80円の3種類の切手がたくさんある。ここから５枚を取り出して切手セットを作りたい。選び方の組み合わせは何通りあるか。ただし、各種類最低１枚は選ぶものとする。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

6通り

［83］解説を見てみよう！

先ほどの問題にもありましたね。
最低一種類系の問題は簡単です。ちょろいです！
なぜなら、組み合わせの可能性を減らしてくれているからです。

５つのうち、３つはもうすでに10円、20円、80円で埋まっています。
なので考えるのは残りの２個分です。

すると考えられる組み合わせは、
全部同じとき：10円–10円、20円–20円、80円–80円
全部違うとき：10円–20円、20円–80円、80円–10円

このように難しいように見える問題も、考え方を変えることで対策できるようになります！
この問題は簡単だったと思うので、これより超むずの問題を欲している方はこちらの問題を解いてみてください。

［84］問題に挑戦！

［84］赤、黒、青のボールペンが各色１ダースずつある。ここから４本選ぶときの色の組み合わせは何通りあるか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

15通り

［84］解説を見てみよう！

さあ、そろそろ計算がめんどくさくなる問題になってきました。
この問題も私は気合の力技で解いていますが、仕切りの考えはここでも使えます。
（詳しい解法は次の問題で行なっています。）

是非、この問題を復習する時は２通りの方法（自力と仕切りの考え）で解いてみてください。
解き方のバリエーションが増えると、ケアレスミスの低下につながります！

場合分けは少なそうなものからやっていくのが鉄則でしたね。
まずは同じ色しかない場合、そして３つが同じ色のとき、２つが同じ色のとき、全部違うときで求めていきましょう。

同じ色しかない場合：赤–赤–赤–赤、白-白-白-白、青–青–青–青
３つが同じ色のとき：赤–赤–赤-白、赤–赤–赤–青、白-白-白-赤、白-白-白-青、青–青–青–赤、青–青–青-白
２つが同じ色のとき：赤–赤-白-白、赤–赤–青–青、青–青-白-白
全部違うとき：赤–赤–青-白、白-白-赤–青、青–青–赤-白

全部合わせて15通りになります！

ちなみに、参考書にかかれている公式は完全無視でOKです。
明日試験があってまだ何もやってないという方はそちらを暗記していくほうがいいかもしれませんが、
そうではないならおすすめしません。

［85］問題に挑戦！

［85］赤、白、ピンクのバラが10本ずつある。ここから10本選んで花束を作りたい。
①２色で作るとき、10本の色の組み合わせは何通りあるか。
②３色をそれぞれ少なくとも2本ずつ使うとき、10本の色の組み合わせは何通りあるか。
③少なくとも赤を3本入れるとき、10本の色の組み合わせは何通りあるか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

①27通り
②15通り
③36通り

［85］解説を見てみよう！

さあついにやってきました。「仕切りの考え方」のお時間です。
今までどうにかこうにか気合でやってきましたが、ここで限界を迎えるはずです。

わかみや先生

私はここで限界を迎えてしまいました（笑）

なので解説していこうと思います。気を引き締めて、ついてきてください！！

①まず初めの問題、これは普通に場合わけで解いていきましょう。
２色の組み合わせは（１本–９本）（２本–８本）（３本–７本）（４本–６本）（５本–５本）の５通りですが、
ここで注意して欲しいのは（１本–９本）（２本–８本）（３本–７本）（４本–６本）には
（９本–１本）（８本–２本）（７本–３本）（６本–４本）の場合も考えられるということです。

なのでこの４通りに２をかけるのを忘れないようにしましょう。
（５本–５本）はそのまま１通りでOKです！これを踏まえた上で計算しましょう。

②ここでも最低2本ずつと言われているので考えるのは残りの4本です。
組み合わせの場合わけは、先ほどもやったように数の少ない方からやっていきましょう！

残り４本のうち、
３つが同じ色のとき：6通り
２つが同じ色のとき：3通り
３つとも違う色のとき：3通り
よって合計で12通りと考えることができます。

さて問題は次です。

③この問題で場合分けの限界を迎えました。
時間内にこれを的確に数え出して、とやるのは流石に厳しいと思います。
そこで、今回ご紹介するのは「仕切りの考え」です！！

仕切りの考え方

順を追って説明していきます。
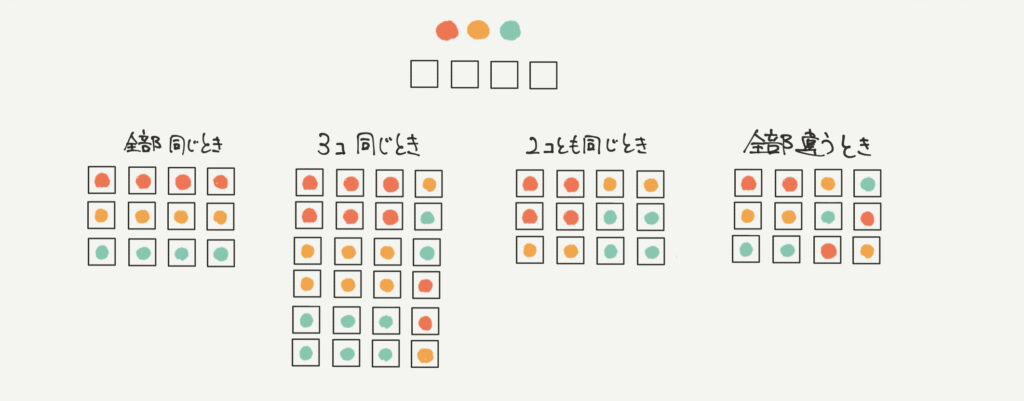
まずは今までの問題にもあった、３種類から４つ取るような問題を考えます。

考えられる可能性は、以下の４パターンです。

全部同じ
３個同じ
２つとも同じ
全部違う

この４パターンに分類されますよね？
これと似た問題が下のような４つの玉と２つの仕切りを組み合わせる問題です。

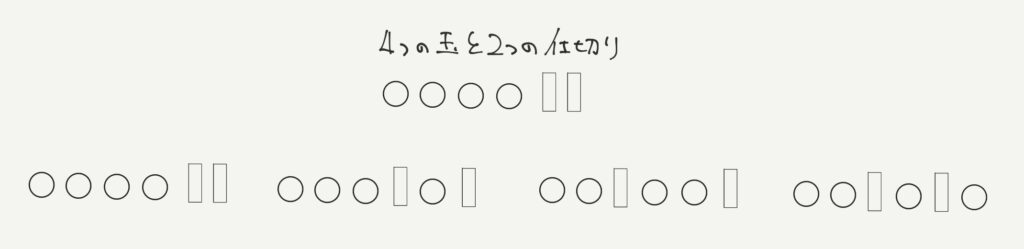
この問題は４個の玉と２枚の仕切り板を合わせた６つのものを並び替える問題です。
一見何の関連もなさそうですが、４つのパターンに注目してみてください。

仕切りが２枚とも端っこで玉が全部同じ位置にある
仕切り板１枚端っこでもう１枚が３個と１個に分けている
仕切り板１枚端っこでもう１枚が２個ずつ分けている
仕切り板２枚が中側にあり、玉を３つに分けている

これ、さっきの色分けのパターンと似てないですか？

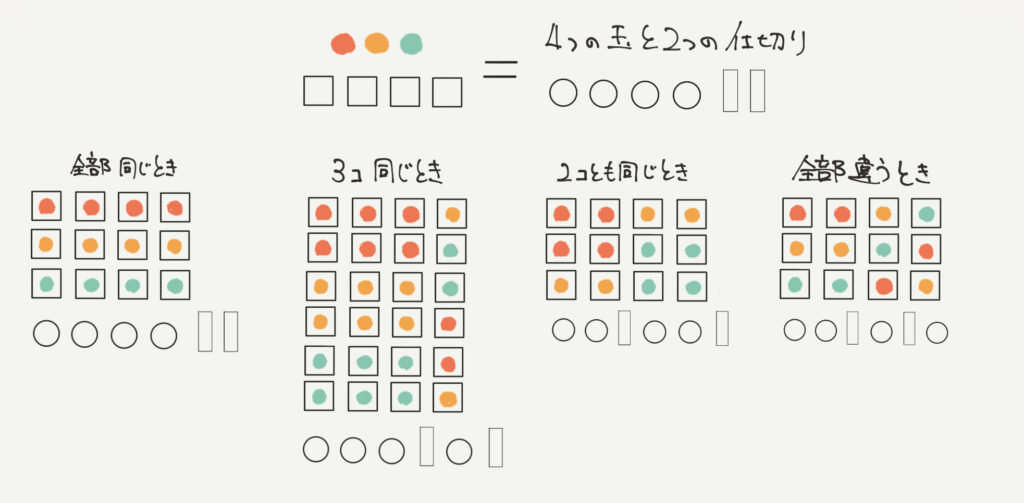
なので、3種類の玉を４つ並べる場合の数は
仕切り板を２枚含んだ６つのものを並び替える問題と同じになります。

これが仕切りの考え方です！ちなみに私は当時この解説を見て感動しました。
ちなみに、今回仕切り板が２枚なのは3種類の玉があるからです。
5種類なら仕切り板は４枚、10種類なら仕切り板は９枚になります。

③の問題の解説に戻ります。
今回空いているスペースは７個で3種類の花を分けるので
仕切り板が２枚、合計９個のスペースに板を入れる場合の数を求めます。

すると ₉C₂となり、答えが36通りと求めることができます。

［86］問題に挑戦！

［86］大人2人と子供6人が手をつないで、輪になりたい。
①8人の並び方は何通りあるか。
②大人2人が向かい合うように、８人で輪になりたい。並び方は何通りあるか。
③大人２人が手をつなぐように、８人で輪になりたい。並び方は何通りあるか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

①5860通り
②720通り
③1440通り

［86］解説を見てみよう！

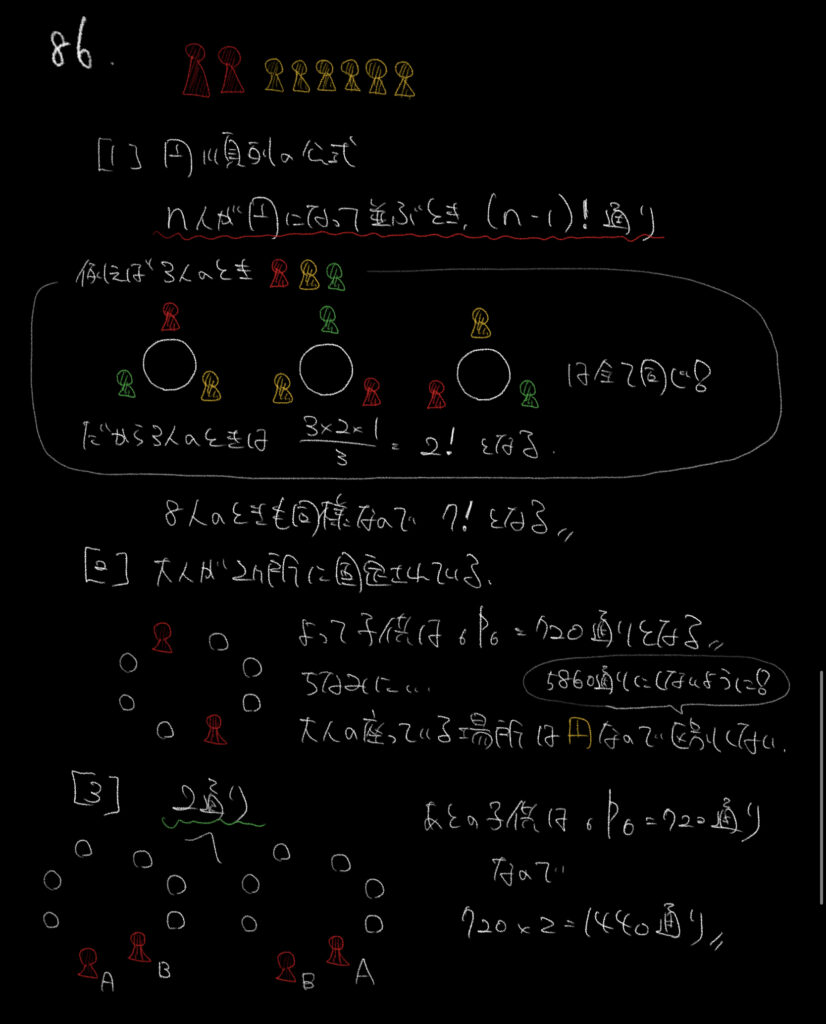
①円順列の公式は覚えているでしょうか？
覚えていなくても解けるとは思いますが、公式の理由だけ頭に入れておきましょう。
例えば、３人で一列になる場合、ボックスの考えで３×2×１＝6通りになりましたね。

n人が円になって並ぶときの場合の数は（n -１）！通りとなります。
例えば5人が円になって並ぶときは4！＝4×3×2×1で24通りとなります。

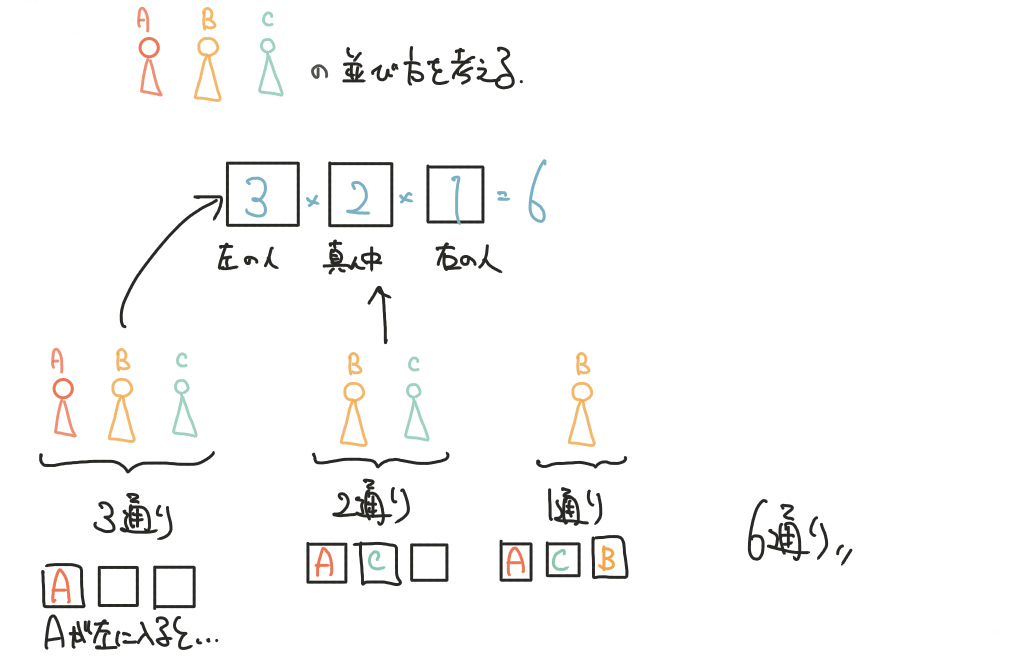
でも円で座る場合、解説の図のように
向きが変わっただけで、並ぶ順番は変わっていないという現象が起こります。

そしてそれは座っている人数分起こります。
今回の例でいうと、３人が座っているので３回重複して計算してしまうということです。
今回は８人が座っているので８回重複して計算してしまいます。よって７！が正解です。

7！＝７×６×５×４×３×2×１
よって、7！＝5860通りになります！

②大人が固定されているので、子供の並び方を考えましょう。
子供は６人いるので6P6＝720通りになります。

大人Aと大人Bの場合の数は考えなくていいのか？

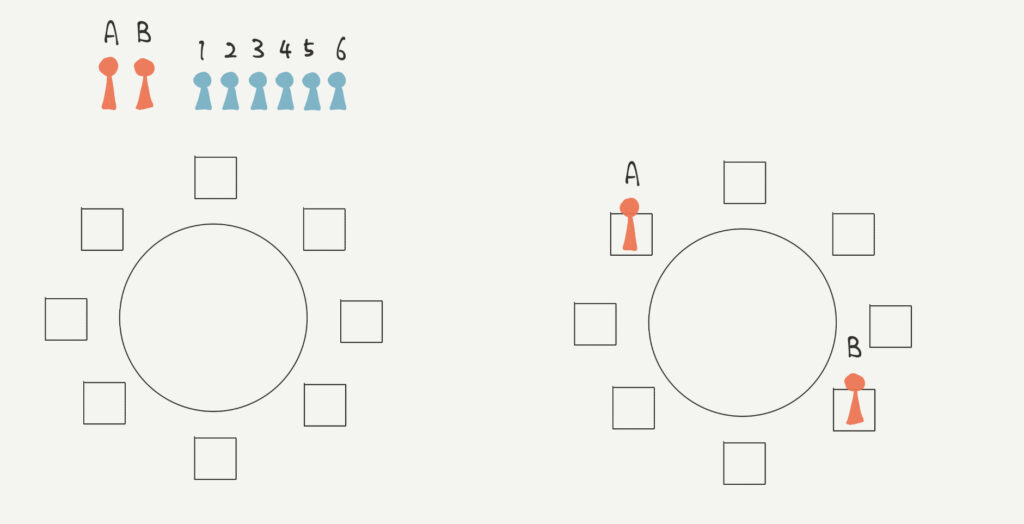
少し難しい話になりますが、子供の6人と大人2名なんだから子供の720通り×大人2人の並び方（2通り）をかけなくていいのか？と疑問に思った方はいませんか？

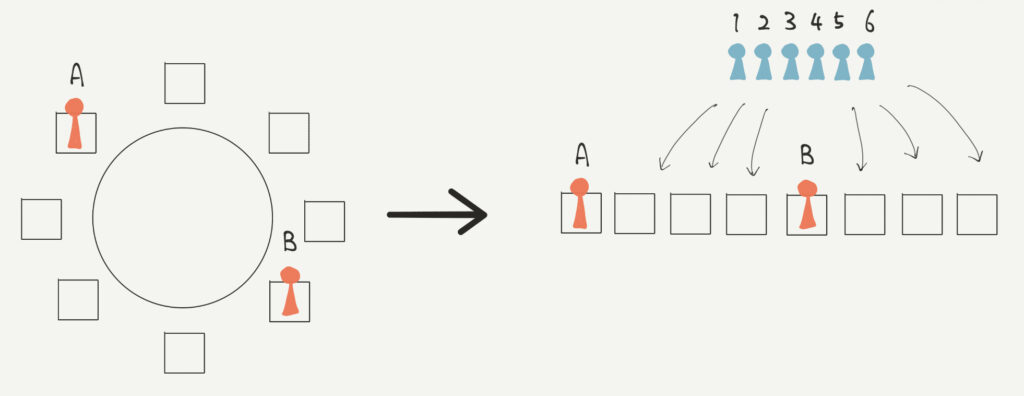
大人Aを基準に円順列をボックスに書き出してみましょう。
大人Bは正反対の位置にいるので子供が入る場合の数だけをまず計算します。

すると6P6＝720通りとなると思います。

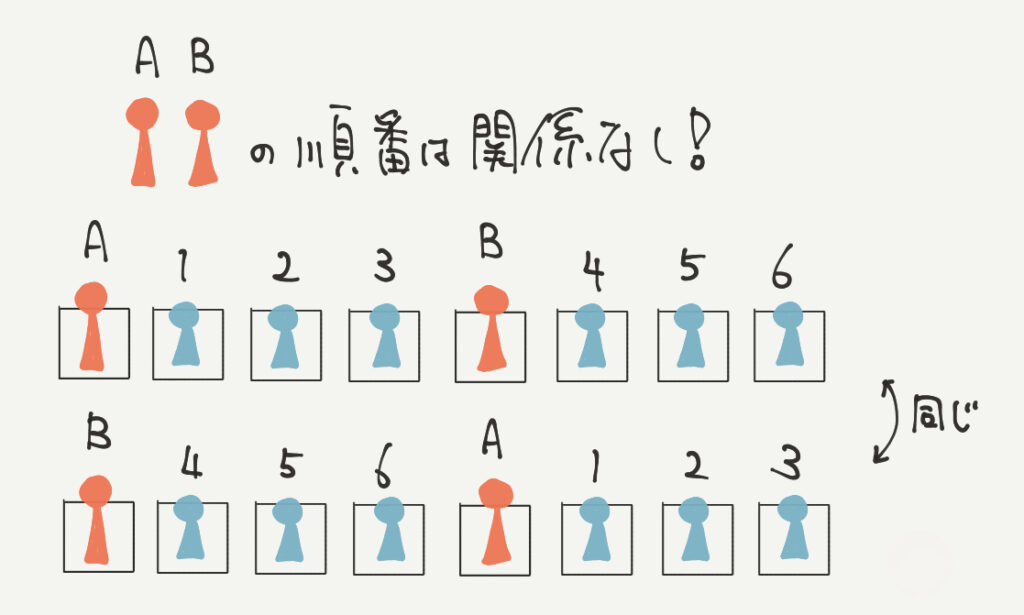
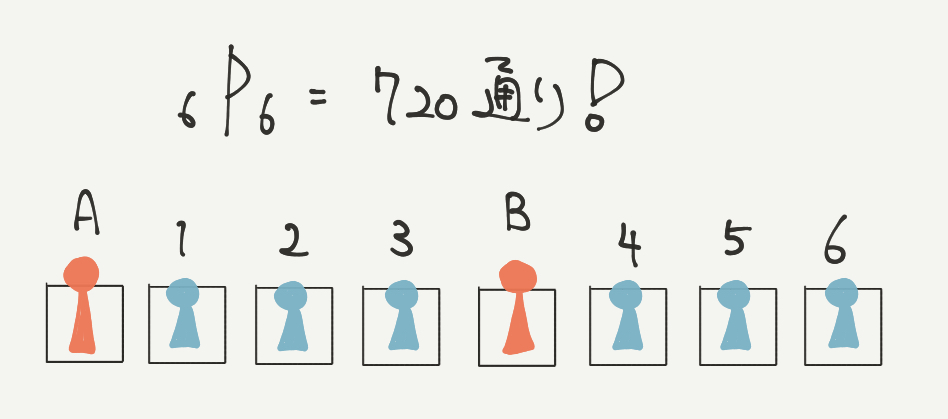
最後に大人Aと大人Bの順番ですが、結論から言うと関係ありません。
上の並び方を見てみてください。
一見違う並び方に見えますが、どちらもAから順番に１２３B４５６という並びですよね？
このようにAとBを固定して考えるだけで、
全員の並び方の場合の数を網羅することができるので計算しなくていいのです！

わかみや先生

相当ややこしい問題なので実際に
一部の並び方を書き出してもいいかもしれませんね。

③最後は大人２人が手を繋ぐときです。これも場所は関係ありません。
ただし大人Aと大人Bの並び方は関係してきます！

これもAを基準に並び方を書き出してみてください。
②と違い、AとBが等間隔で離れていないため、重複が発生しなくなります。

あとは②でもやったように子供の場合の数を求めれば、
720×2＝1440通りと求めることができます。

まとめ

いかがでしたか？今回の単元で重要だったのは何と言っても「仕切りの考え方」でしたね！！
この考えを理解していれば、私のように気合で解き進めることなくサクサク問題を解くことができます。

ぜひ使いこなせるように復習を徹底してみてください！
そして悲しいことに円順列と重複の問題はもう少し続きます（泣）

問題集の攻略、頑張っていきましょう！

参考になったらぜひシェアお願いします！

URLをコピーしました！

URLをコピーしました！

【SPI試験徹底対策】円順列、重複の問題攻略法を解説！仕切りの考え方を活用せよ！（全５問）

はじめに

［82］問題に挑戦！

［82］解説を見てみよう！

［83］問題に挑戦！

［83］解説を見てみよう！

［84］問題に挑戦！

［84］解説を見てみよう！

［85］問題に挑戦！

［85］解説を見てみよう！

仕切りの考え方

［86］問題に挑戦！

［86］解説を見てみよう！

大人Aと大人Bの場合の数は考えなくていいのか？

まとめ

関連記事

解き方から問題に挑戦