はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験のSPI対策として主に数学(算数)に関する
情報やコツをお届けしていきたいと思います!
SPIを勉強していると中学受験や高校受験を思い出しますよね。
特にSPIでは「場合の数」や「確率」の単元が頻出される印象があります。
多くの皆さんも同じだと思いますが、小学生や中学生だった頃
一番嫌いだった算数/数学の単元が「場合の数」と「確率」でした。
なぜよりにもよってこの単元なんだ・・・と何度思ったことか。
平面図形とかもっと出してくれ〜なんて思っていました(笑)
ですが、そんな泣き言も言えませんので1つ1つ苦手を攻略していくしか道はないですね。
微力ですが、一緒に頑張って勉強してきましょう!
この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
[74]問題に挑戦!
答えを見るにはここをクリック!
①288通り
②24通り
③144通り
④528通り
[74]解説を見てみよう!
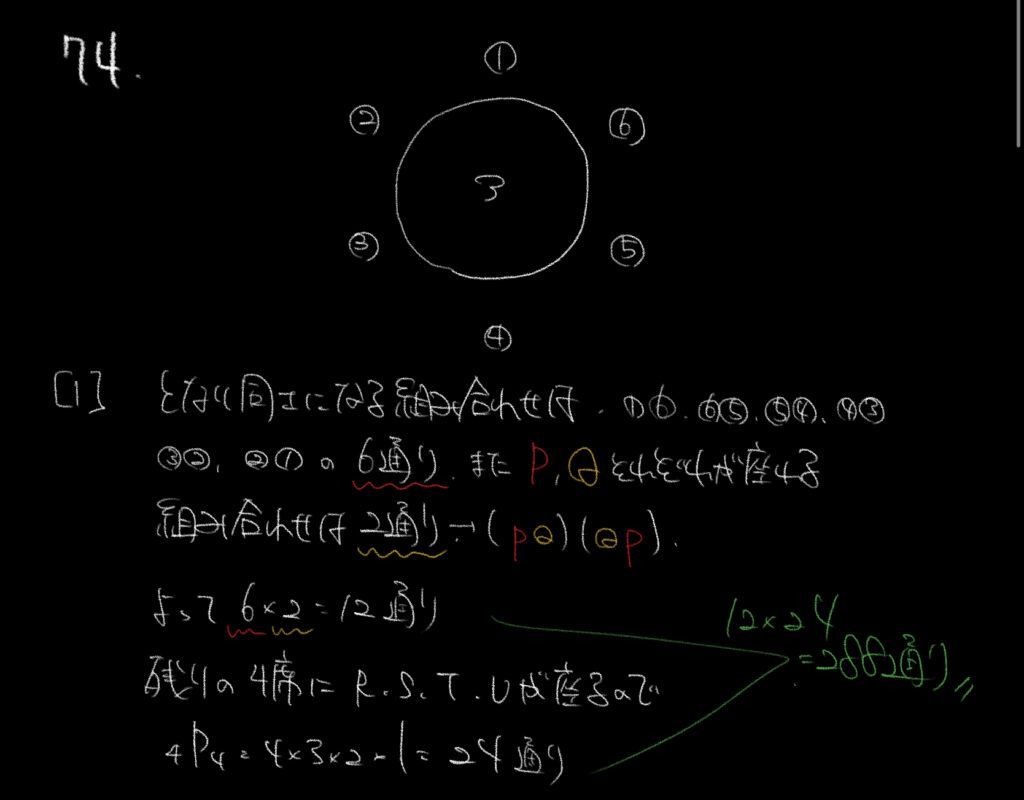

この単元はじめの問題は席順の問題でした。
①1つずつ順番に考えてみましょう!
まず初めに、隣同士になる場合は1-6、6-5、5-4、4-3、3-2、2-1の6通り。(メモが見づらくてすいません!)
それぞれPQで座る場合とQPで座る場合の2通りがあるので、組合せは12通りです!
ここで満足してはいけません。
残り4席に座るR,S,T,Uの4人について考えてみましょう。
4人が残った4席に座る場合の数は4×3×2×1=24通りです。
よって12×24=288通りと出すことができます。
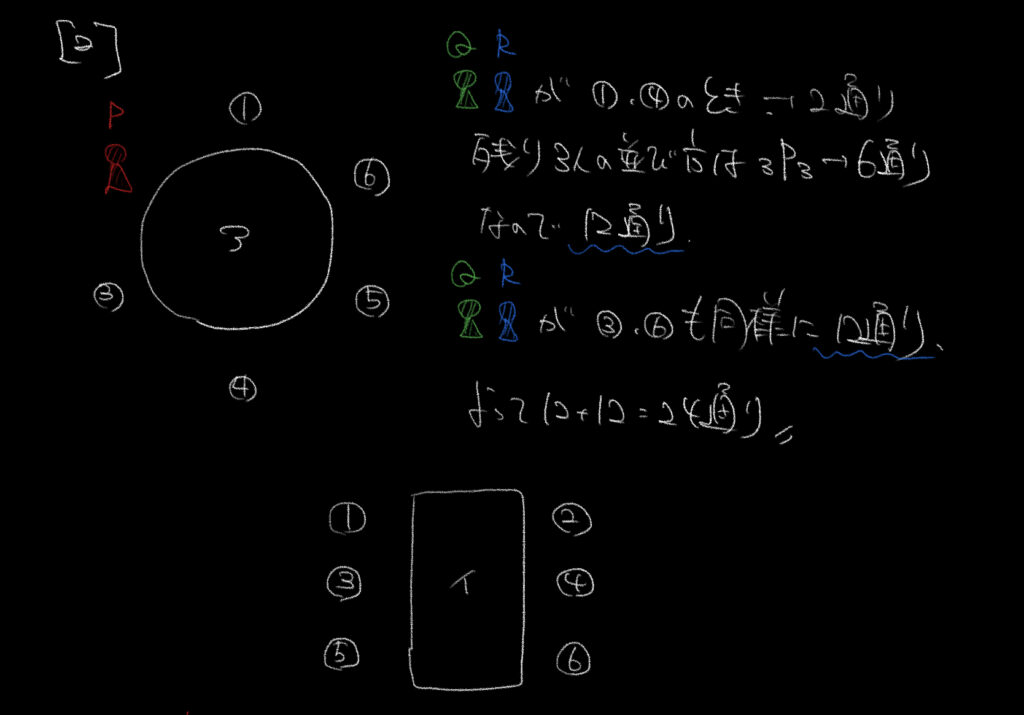
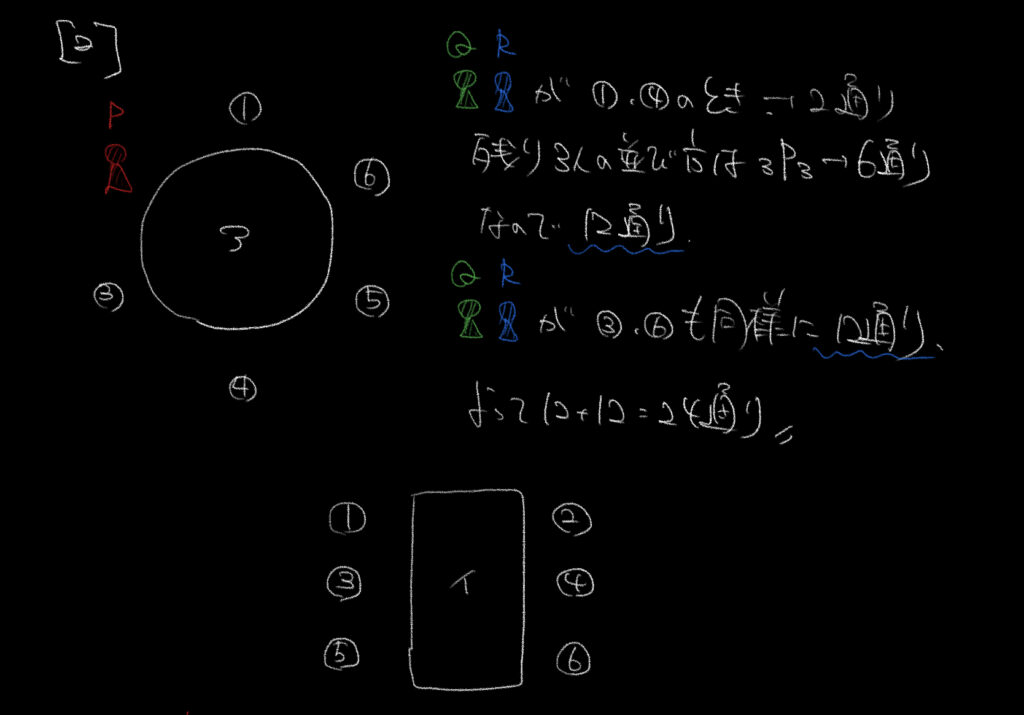
②QRの場所について、2人が向かい合うためには2人が1-4か3-6のときだけです。
(2-5はPが座っているので使えません。)
先ほどと同様に、QRの座り方は2通り、Pが座っているので残りの座る人は3P3で6通りの座り方があります。
また1-4の時、3-6の時と2通りあるので合計で
2×2×6=24通りとなります。
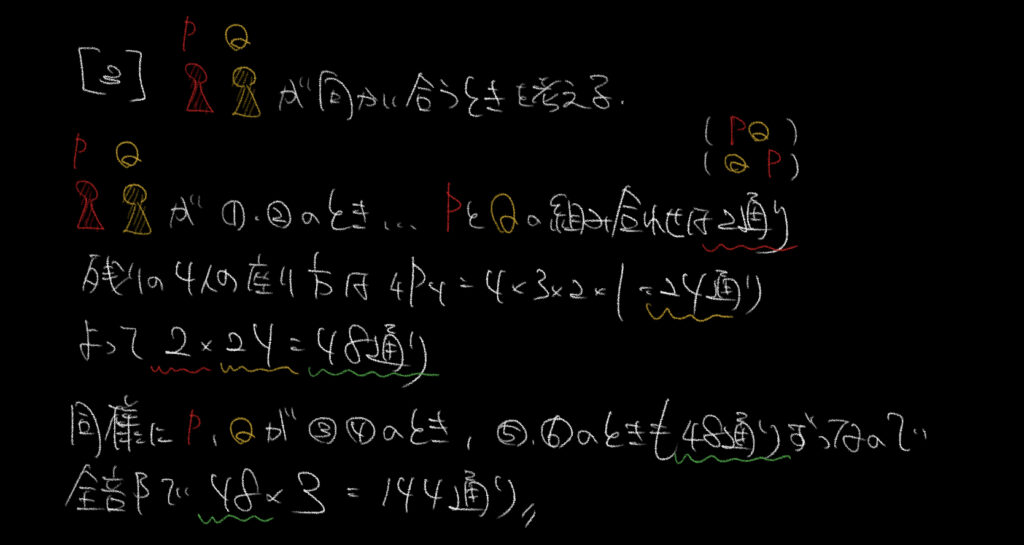
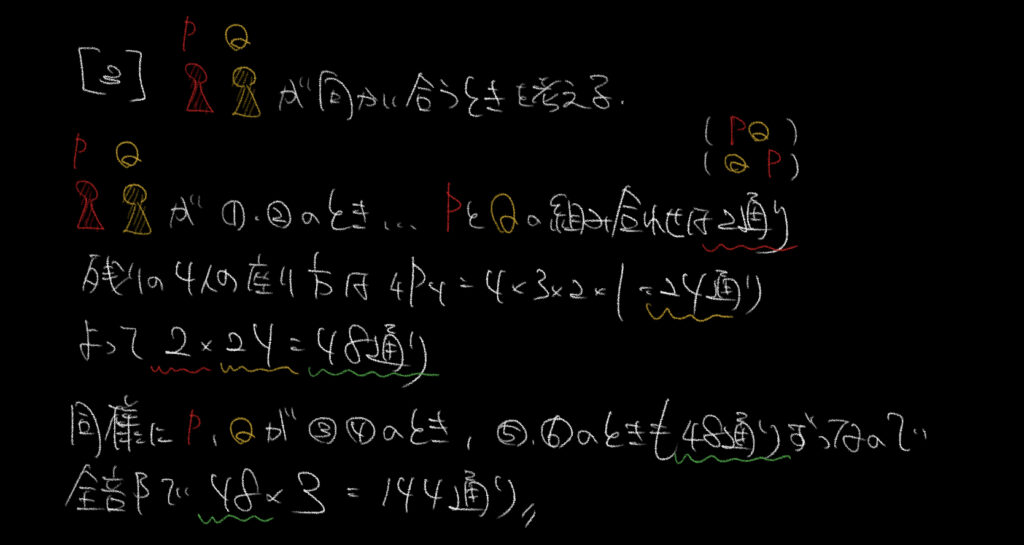
③ここから、席が円形ではなくなってしまいます。
ここに気をつけて解いていきましょう。
先ほどと同じ考え方で、PQが向かい合うのは1-2と3-4と5-6の3通りです。
また、それぞれPQの順で座るのかQPで座るのかで分かれるので2人の座り方も2通りあります。
そして最後に残りの4人の座り方が4P4で24通りとわかるので、
2×3×24=144通りとわかります。


④余事象の復習です。
全体からPQが隣同士になる場合の数を引けば
PQが隣同士にならない場合の数を求めることができます。
全体の場合の数は6P6=720通り!
PQが隣同士になる場合の数は、
PQが1-3と3-5と2-4と4-6の4通り。
それぞれの座り方はPQとQPの2通りをかけて4通り×2通り=8通り!
残りの4人(R ,S ,T,U)の座り方は4P4=24通り。
よって8×24=192通りになります。
全体からPQが隣同士になる場合の数を引いて
720−192=528通りとなります。

[75]問題に挑戦!
答えを見るにはここをクリック!
①6通り
②24通り
[75]解説を見てみよう!


中学受験で最も頻繁に出る色分けの問題とそっくりです。
手順を①②③④と書いたのでそれに沿って解説を読んでみてください。
(1)まず初めに塗れる色は全部で3色。
ここで赤を塗ったと仮定しましょう。
次にぬれる色は青と黄の2色になります。ここで青を塗ると、
次もその次も塗れる色が1通りになります。
よって3×2×1×1×1=6通り。
(2)も同様です。まず塗れる色は4色。
ここで青を塗ったと仮定しましょう。
次に入るのは3色でここに黄が入ったとします。
最後にぬれる色は赤か、緑の2通りです。
よって、4×3×2=24通りになります。


[76]問題に挑戦!
答えを見るにはここをクリック!
①48通り
②144通り
[76]解説を見てみよう!


①女性が真ん中のときの場合の数です。
この時考えるのは女性の並び方と男性の並び方です。
女性は解説にも書いてあるように2通りの並び方があります。
一方で男性は4×3×2×1=24通りの並び方があります。
このことから女性を真ん中にする並び方は全部で48通りあることがわかります。
②こちらの方が難しかったと思います。
まず前列後列での並び方はそれぞれ6通り(3P3)ずつあります。
そして忘れてはいけないのが、前列にいく男性を選ぶことです。
男性4人の中から、前列にいく男性を1人選ぶので4通り。
よって6×6×4=144通りであることがわかります。


[77]問題に挑戦!
答えを見るにはここをクリック!
①12通り
②20通り
[77]解説を見てみよう!

この問題、結構めんどくさいですよね。
私もこの問題にかなり時間を割かれたのを覚えています。頑張っていきましょう!
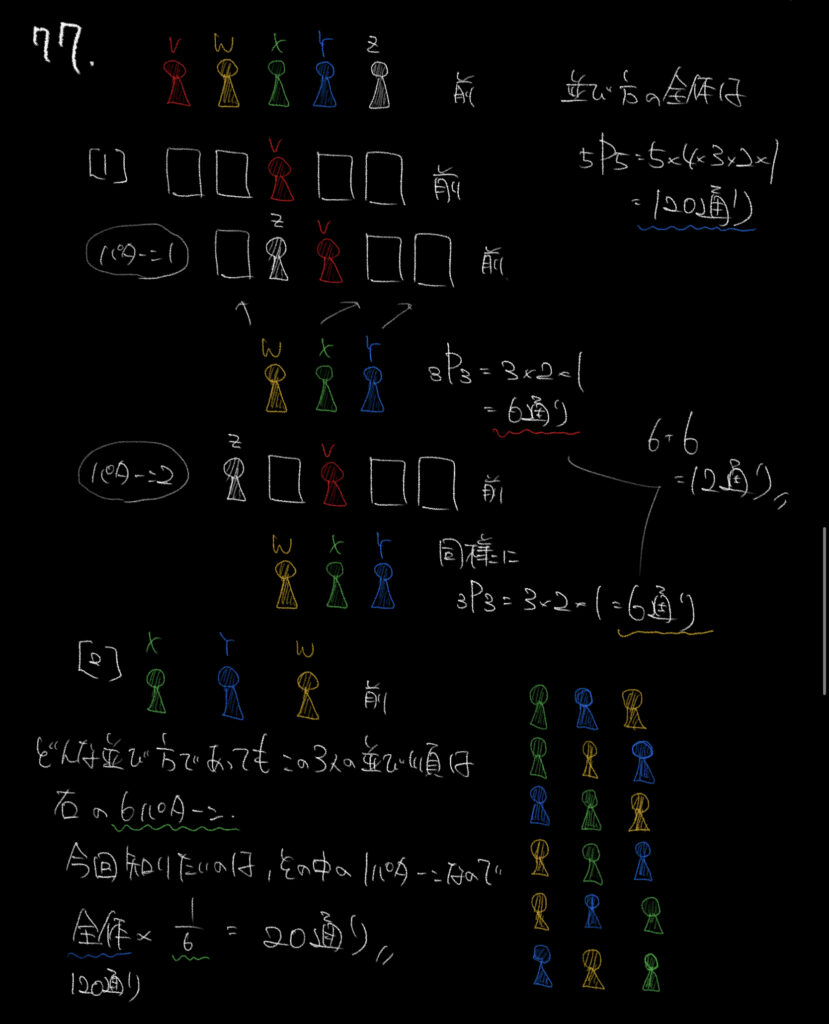
①の問題は場合分けで解いていきます。
3番目にVが並んでいる時、Zは4番目か5番目にいるはずです。
<パターン1>4番目の場合、残った3人の並び方は3×2×1=6通りあります。
<パターン2>同じように5番目に並んでいても3×2×1=6通りです。
よって6+6=12通りと求めることができます。
別解では少し賢いやり方で解いています。
②で使う考えと同じなので頭に入れておきましょう。
Vが真ん中に立っている時、4人の並び方は12+12=24通りあります。
この24通りのうち、Zが後ろにいるのは半分の12通りであることがわかります。
24通りの半分で12通りとなりますが
Vが2番目、4番目に立っている時は半分ではないので図を書いて気をつけましょう。
②は全体からX,Y,Wの並び順のうち、当てはまるものを選びます。
VとZを一旦無視して考えると、どんな並び順であれ、XYWの並び方は解説の6パターンしかありません。
なので全体の並び方120通りを6で割った20通りが答えとなります。




まとめ
いかがでしたでしょうか?
以上がSPI対策の席決め、塗り分けの問題でした。
このように一見難しい内容でも、きちんと図を書いて場合分けすることが重要でしたね。
これをしないとこんがらがって考えてしまい、時間もかかる上に正解できなくなってしまいます。
今回特に難しかったのが最後の問題でした。
別解のやり方を押さえておくと次のカード、コイン、サイコロの問題が楽になります。
一度ここで復習しましょう!
順列・組合せもあともう少しです!頑張っていきましょう。









