【SPI試験徹底対策】円順列、重複の問題攻略法を解説！場合分けのコツを駆使してケアレスミスをなくそう！（全５問）

2023年11月29日

はじめに

わかみや先生

みなさん、こんにちは！「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います！

円順列や重複に関する問題のパート２になります。
パート１から勉強したい皆さんはこちらの記事からぜひチェックしてみてください。

［87］問題に挑戦！

［87］X,Y,Zの３つの箱に６個のミカン全部を入れる場合、入れ方のパターンは何通りあるか。
ただし、使わない箱があってもよい。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

27通り

［87］解説を見てみよう！

円順列、重複の後編です！
ここからの問題は前回の記事で勉強した「仕切りの考え」よりも「場合分け」重視で解いていきます。
最終的にどちらの方法がやりやすいのかは個人差があると思うので、自分が解きやすい方法で解くといいでしょう。

まずはこちらの問題です。
数え忘れ、数えすぎのないように（XYZ）の順番で考えています。

（XYZ）の組み合わせのうち、数字が2個同じ場合の場合の数は３通りになります。
（６-０-０）（０-６-0）（０-０-６）のような感じです。

一方で３つの数が違うときは６通りあります。
（５-１-０）（１-０-５）（１-5-０）（５-０-１）（０-１-５）（０-５-１）みたいな感じです！

これらを計算することで答えを求めましょう！

［88］問題に挑戦！

［88］赤皿２枚、白皿２枚、青皿１枚がある。これをA,B,C,D,Eの５つに区切られた陳列棚に１枚ずつ飾りたい。皿の並べ方は何通りあるか。ただし、同色の色に区別はないものとする。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

30通り

［88］解説を見てみよう！

考え方は今まで通りです。順番にやっていきましょう。

STEP1：まずは赤皿２枚を５つの棚のどれか２つにしまいます。
５つの中から２つ選んでいて、順番は関係ないので組み合わせの式を使いましょう。
5C2となりますので、５つの場所から2枚の皿を入れる場合の数は10通りと計算できます。

STEP2：残った３つの棚の中から白皿を入れる２つを選びます。先程と同様にやりましょう。
すると3C2=3C1となりますので、３つの場所から2枚の皿を入れる場合の数は3通りとなります。

残った１つに最後のお皿が入りますので、最後は計算しなくて大丈夫です！
これらの場合のを合わせて、10通り×3通り＝30通りが答えとなります。

ちなみにこのお皿を入れる順番は全く関係ないです。
はじめに青皿を入れてもいいですし、赤皿を最後にしても計算結果は変わりません！

［89］問題に挑戦！

［89］男性3人と女性3人がいる。
①男女が交互になるように一列に並びたい。並び方は何通りあるか。
②男性3人が隣り合うように、一列に並びたい。並び方は何通りあるか。
③男女が交互になるように、6人で輪になりたい。並び方は何通りあるか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

①72通り
②144通り
③12通り

［89］解説を見てみよう！

①交互に並ぶので場合分けで解いていきます。

まずは男子が左にいる状態の場合の数を求めましょう。
図にも書いてある通り、まずはじめに男子が3人、次に女子が3人、残った男子2人、
残った女子2人、最後に男女1人ずつといった風に計算で求めることができます。
すると男子が左にいる状態の場合の数は36通りとなります。

左が女子のときの場合の数も同様に36通りあるので合計で72通りと求まります。

②男子3人を１グループとして考えます。考えられる可能性は解説の図にある４パターンの並び順です。
１グループで考えているとはいますが、１グループには男子も3人並んでいます。
なので男子の並び順を考えましょう。

男子の並び順は男3人が並ぶので3×2×1=6通りです。

また、女子の並び順も同様に6通りとなりますので、
考えると、4×6×6＝144通りとなります。

③最後は円順列の復習です。
前回の記事の［86］にも書きましたが、円順列の場合、「並んでいる人数」倍だけ多く数えてしまうので、
今回は①で求めた全体の場合の数の72通りを全体人数の6人で割って12通りと答えを求めましょう。

［90］問題に挑戦！

［90］3種類のワインが用意されている試飲会があった。1種類について1人１回、最大３回の試飲ができる。
①P1人が試飲するとき、ワインの種類の選び方は何通りあるか。ただし、最低１回は試飲するものとする。
②PとQの2人があわせて４回試飲するとき、PとQが飲むワインの種類の組み合わせは何通りあるか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

①7通り
②15通り

［90］解説を見てみよう！

①これも場合分けでバシバシ解いていきましょう！！

今回の場合分けはPが１回試飲する、２回試飲する、３回試飲するの３パターン考えられます。
場合分けで考えるときは、数が少ないものから順番に数えていくことが重要でしたね。

まずは１回試飲するときを考えます。これは当然３通りしかありません。
そして２回試飲するときも同様です。調べ上げて３通りと答えを出しましょう。
最後に３回試飲するときを考えましょう。これは１通りとわかりました。

よって合計した7通りが答えとなります。

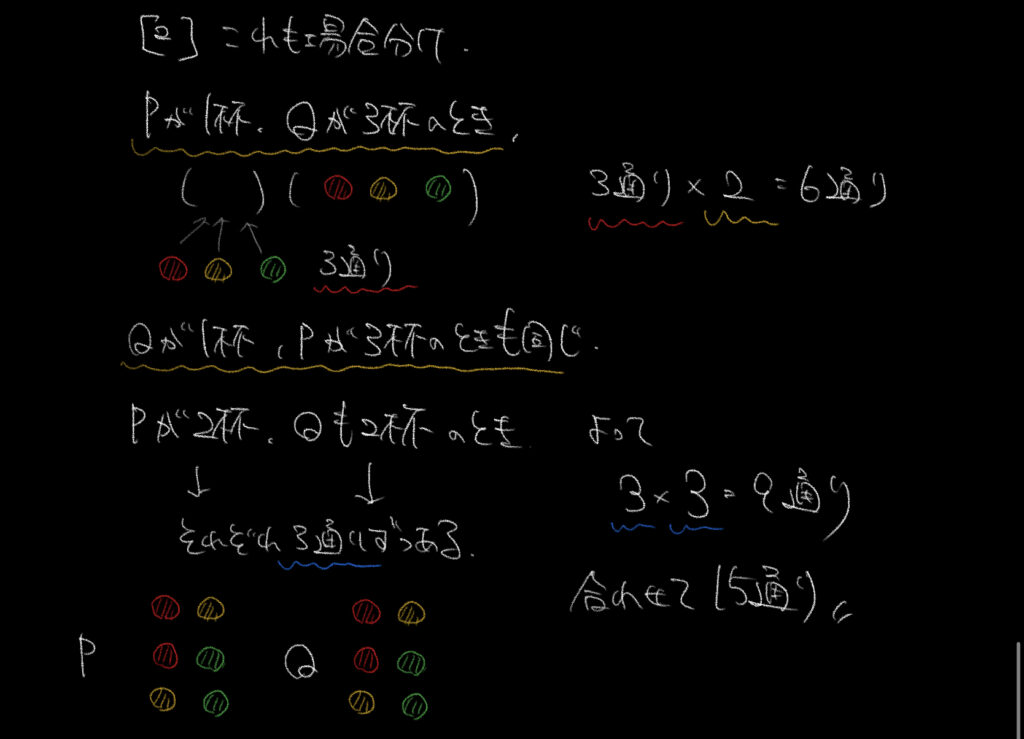
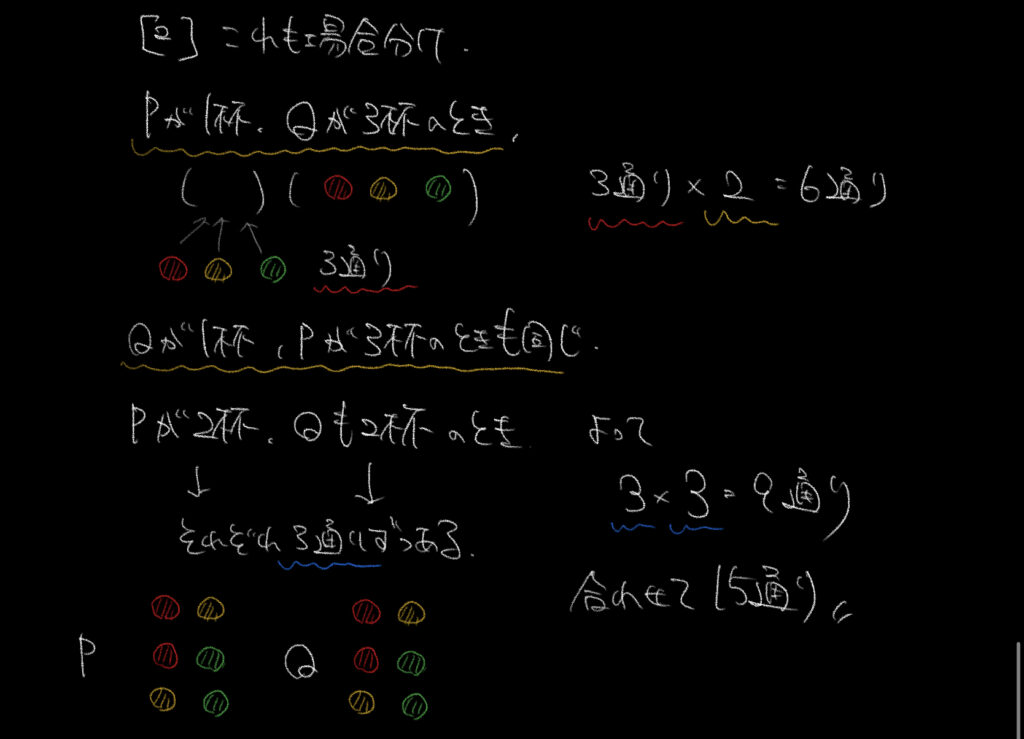
②の問題も「場合分け」です。

まずPQが何杯ずつ飲んだのかを場合分けしましょう。

考えられる可能性は
（PQ）＝（１杯-３杯）（２杯-２杯）（３杯-１杯）の３パターンです。
（１杯-３杯）（３杯-１杯）のときを考えます。

１種類につき１杯までしか飲めないことが問題文に書いてありますので、
３杯飲む＝３種類のワイン（⚫︎–⚫︎–⚫︎）全部1回ずつ飲んでいることになります。

つまりワインを飲む組み合わせは、
（⚫︎–⚫︎–⚫︎）（⚫︎）
（⚫︎–⚫︎–⚫︎）（⚫︎）
（⚫︎–⚫︎–⚫︎）（⚫︎）
3通りと求められます。
ここから、（１杯-３杯）（３杯-１杯）のときの場合の数は３通り×２パターンの６通り。

また（２杯-２杯）のときは①で求めた３通りを使って3×3＝9通りと求めることができます。
これらを全て合わせた15通りが答えです。

［91］問題に挑戦！

［91］洋菓子が5種類、和菓子が3種類ある。ここから何個か選んで、１箱に詰め合わせたい。
①1種類を4個ずつ、合計12個を詰めるときの入れ方は何通りあるか。
②1種類を同じ数ずつ選ぶようにして、洋菓子と和菓子を8個ずつ、合計16個を詰めるときの入れ方は何通りあるか。
③洋菓子と和菓子を3個ずつ、合計6個を詰めるときの入れ方は何通りあるか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

①56通り
②45通り
③350通り

［91］解説を見てみよう！

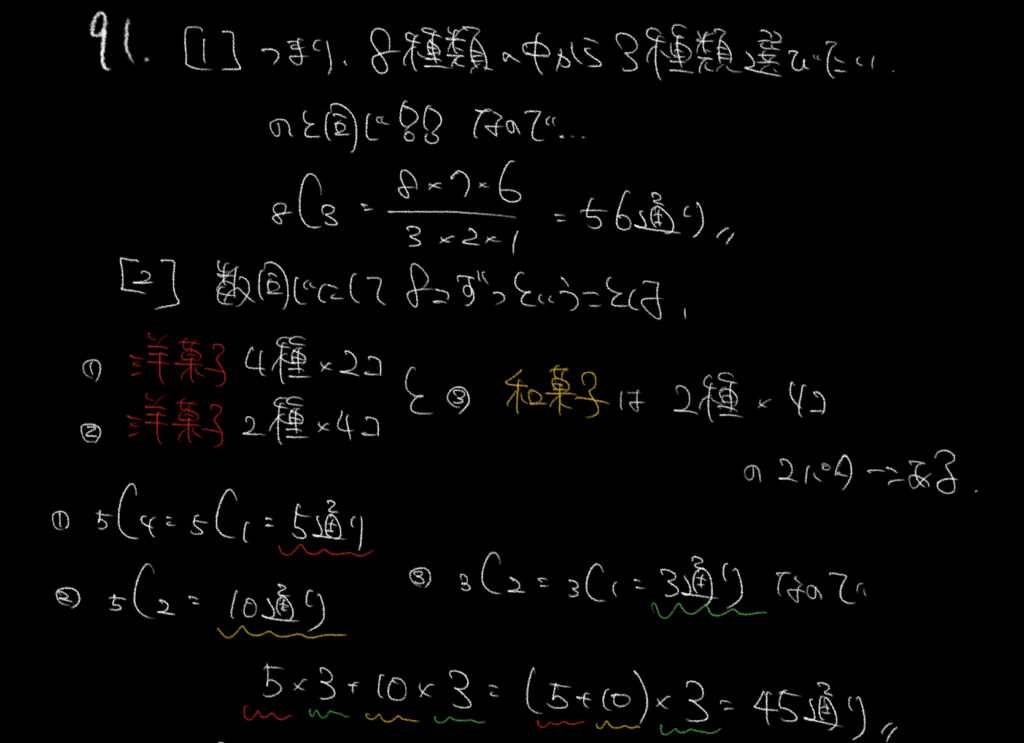
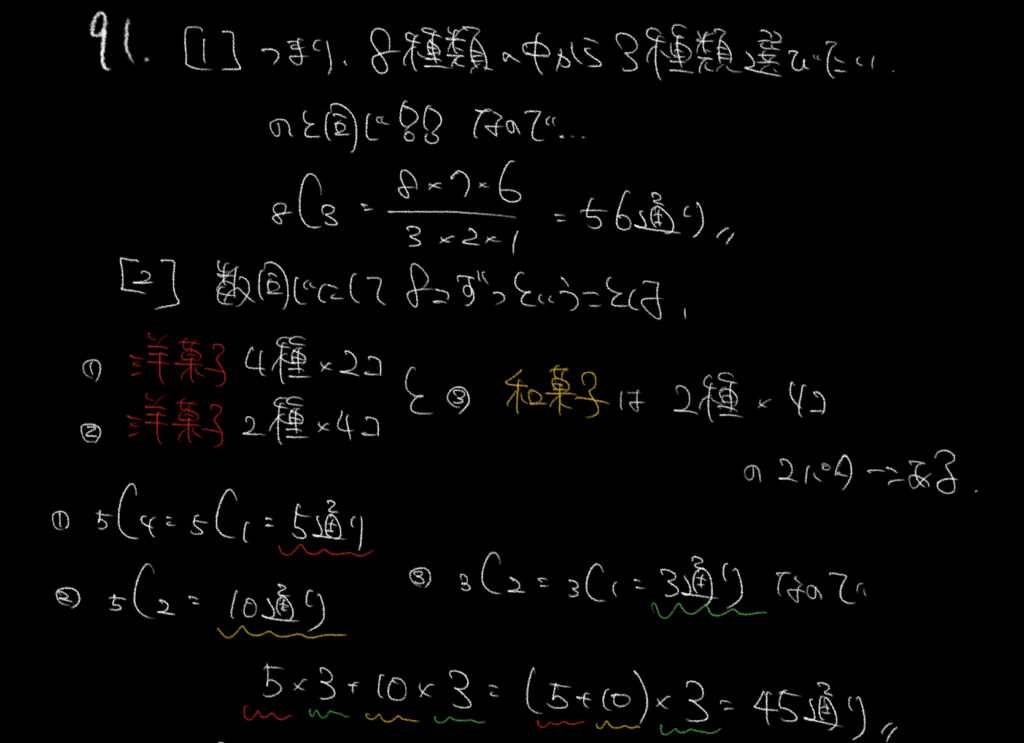
①1種類につき4個で合計12個のお菓子なので言い換えると、
8種類のお菓子の中から3種類を選べということになります。
これも順番は関係ないので、組み合わせの式で解くことができます！
8C3=56通りとサクッと求めましょう！

②ここから少し面倒になってきます。
同じ数ずつで8個ということは、洋菓子なら4種類を2個ずつ、2種類を4個ずつの２通りの考え方ができます。
一方で和菓子は3種類しかないので2種類を4個ずつ選ぶしかありません。

これらを場合分けで計算したものが解説になります。
・洋菓子→4種類を2個ずつ、和菓子→2種類を4個ずつ
・洋菓子→2種類を4個ずつ、和菓子→2種類を4個ずつ
の２通りを考えて、答えを求めましょう。

＜洋菓子→4種類を2個ずつ＞
５種類の中から４種類を選ぶ＝「選ばない１種類」を選ぶので、5C4=5C1で5通り。

＜洋菓子→2種類を4個ずつ＞
５種類の中から２種類を選ぶ＝5C2で10通り。

＜和菓子→2種類を4個ずつ＞
３種類の中から２種類を選ぶ＝「選ばない１種類」を選ぶので、3C2=3C1で3通り。

よってこれらの場合の数をそれぞれ計算して、45通りとなります。
・洋菓子→4種類を2個ずつ、和菓子→2種類を4個ずつ　15通り：5通り×3通り
・洋菓子→2種類を4個ずつ、和菓子→2種類を4個ずつ　30通り：10通り×3通り

③最後にして一番面倒な問題でした。

洋菓子と和菓子を3個ずつ、合計6個を詰めるときの入れ方について
洋菓子、和菓子それぞれの場合で考えてみましょう。

まず洋菓子３つについて、
・全部同じのとき
・全部違うとき
・2個同じとき
の３パターンがあります。

それぞれ、
・全部同じのとき→洋菓子の種類は5種類しかないので５通り。
・全部違うとき→5種類の中から選ばない２つを選ぶ＝5C2なので10通り。
・2個同じとき→ボックスの考えを使って5通り×1通り×4通り＝20通り。

合計で洋菓子を詰める場合の数は35通りとわかりました。

5通り×1通り×4通り＝20通り
5通り→はじめのボックスに入る種類は5通り
1通り→2個同じときを考えたいので、次のボックスに入るお菓子の種類は１つ目のボックスと同じ。よって1通り。
4通り→最後のボックスに入るお菓子は１つ目以外であればなんでもいいので4通り。
和菓子についても見ていくと、

同じように和菓子でも考えていくと、
・全部同じのとき→和菓子は3種類しかないので3通り。
・全部違うとき→3種類なので1通りしかない。
・2個同じとき→ボックスの考えより6通り。

合計で和菓子を詰める場合の数は10通りとわかりました。
よって35通り×10通り＝350通りと答えを求めることができます。

まとめ

以上で円順列、重複は本当に終わりです！！お疲れ様でした！
この解説からもわかるように、こういう問題は解き方がいくつかあります。

今回の記事では「場合分け」に注目して解いていきましたが、
必ずしもこのやり方しかないわけではありません。

解説を通じて自分が一番ミスをせず、賢く解くことのできるやり方を見つけてみてください。
SPIに限らず勉強は、自分が効率よく学習できる方法を探す作業だと思いますので、
ぜひ問題を解き進めていく中でご自身にあった解き方を見つけてみてください。

次回からはみんな大嫌いな確率です笑
お楽しみに！

参考になったらぜひシェアお願いします！

URLをコピーしました！

URLをコピーしました！

【SPI試験徹底対策】円順列、重複の問題攻略法を解説！場合分けのコツを駆使してケアレスミスをなくそう！（全５問）

はじめに

［87］問題に挑戦！

［87］解説を見てみよう！

［88］問題に挑戦！

［88］解説を見てみよう！

［89］問題に挑戦！

［89］解説を見てみよう！

［90］問題に挑戦！

［90］解説を見てみよう！

［91］問題に挑戦！

［91］解説を見てみよう！

まとめ

関連記事

解き方から問題に挑戦