はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います!
今日勉強する問題はカードやサイコロ、コインが出てくる問題になります。
カードを組み合わせて数字を作ったり、
コインやサイコロを何個か転がして場合の数を求めさせたりする問題です。
この記事では中学受験で出てくる「数の性質」という単元が非常に大事になってきます!
全ての問題で共通するポイントは、問題文を図やイメージに落とし込むということです。
頭の中で計算してしまうとケアレスミスや計算の抜け漏れが発生しますので、
テスト本番はともかく、必ず勉強するときはお絵かきをしながらとき進めるようにしましょう。
この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
[78]問題に挑戦!
答えを見るにはここをクリック!
①360通り
②60通り
③216通り
[78]解説を見てみよう!
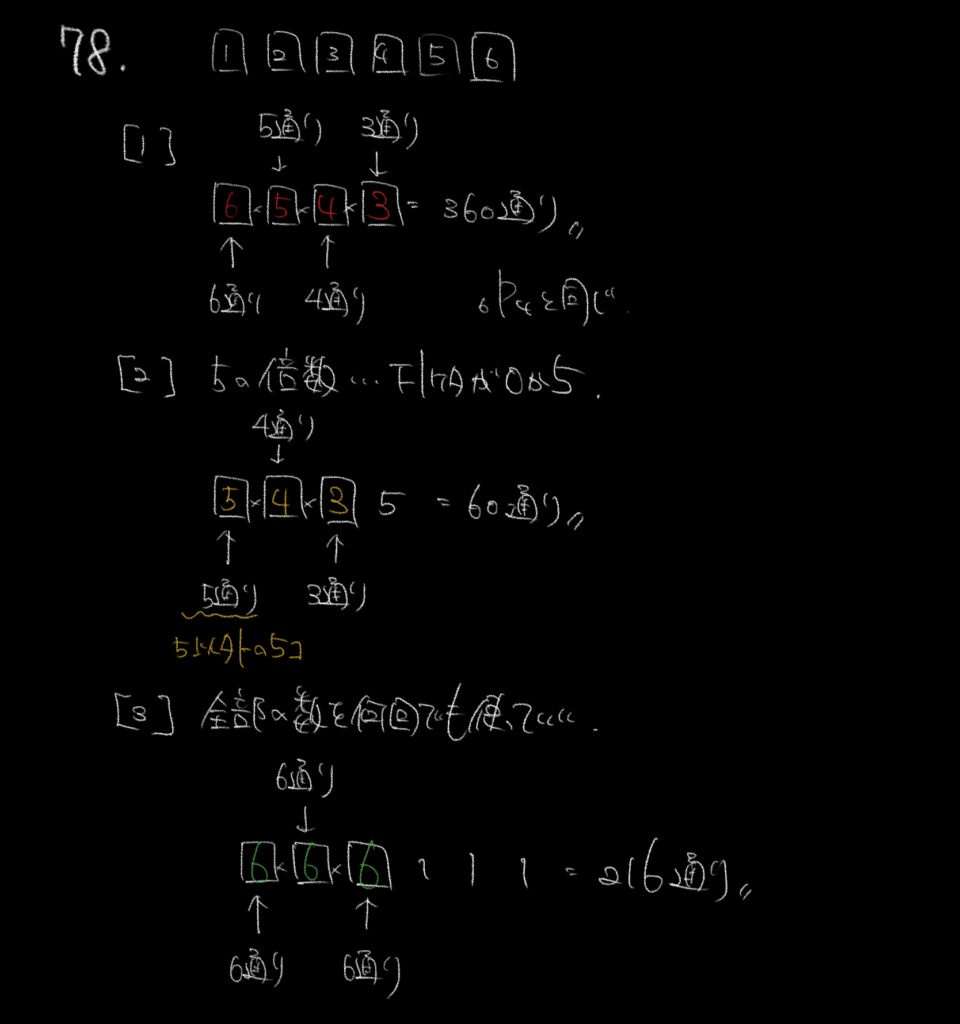
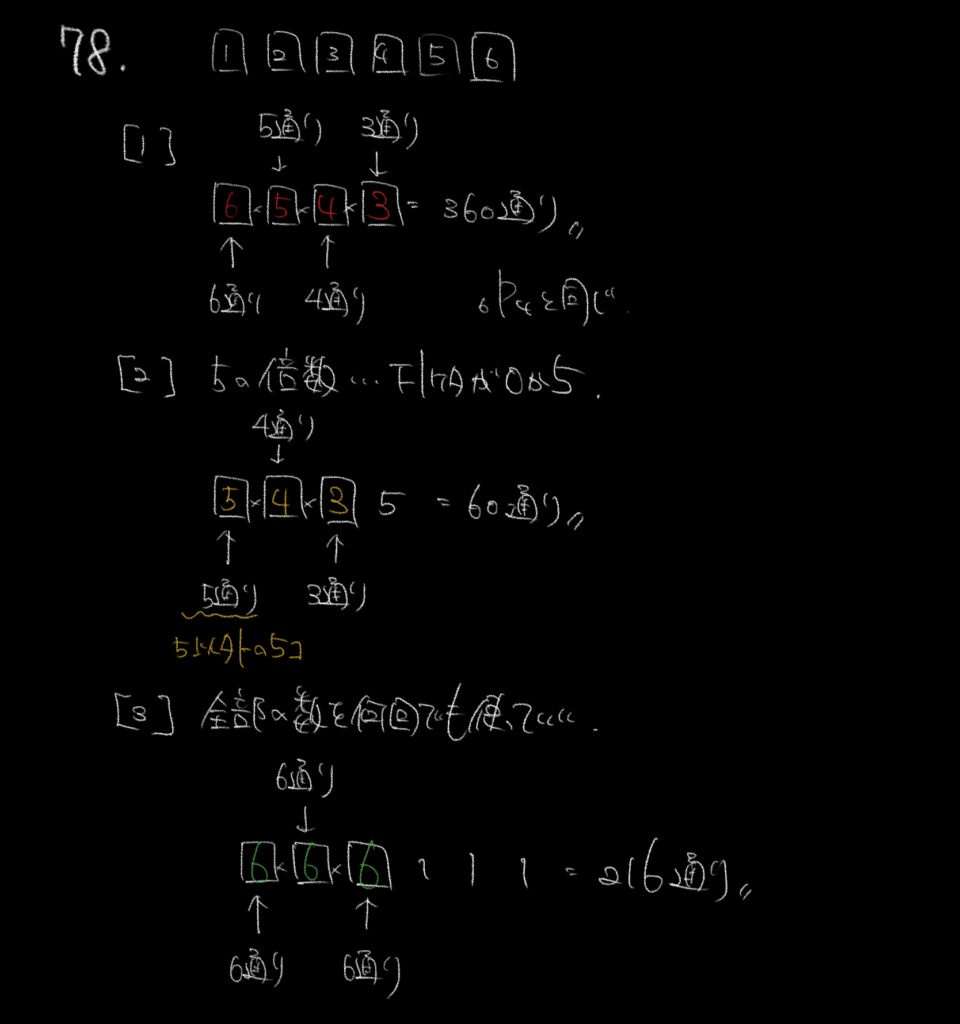
数字の並べ替え問題です。
①ボックスの考えを使って、当てはまる数字を考えてきましょう。
ちなみにSPI対策のボックスの考えとは、◻︎(ボックス:箱)をかくコツのことです。
並ぶ順番や選ぶ組み合わせを考える際に便利な考え方になります。
この考えを理解することでSPIの数学の問題にも対処できます。


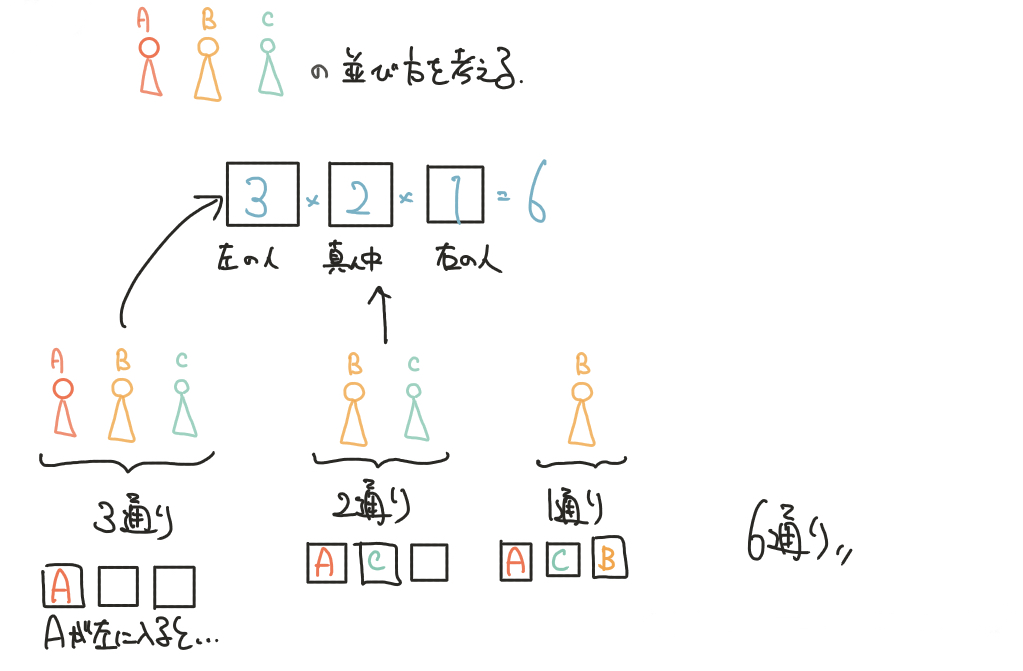

例えばこのようなABCの3人が横一列に並ぶときに左に入る可能性があるのはABCの3通り。
次に、真ん中に入る可能性があるのがBCの2通り。
最後に入るのは必ず残っている人なので1通りとなります。
この考えを実際の問題に適用してみましょう。
同じ数字を使ってはいけないので初めの数字は6通り、そこから5、4、3通りとなります。
よって数字が異なる4けたの整数は、6×5×4×3=360通りになります。
②5の倍数の性質ご存知ですか?
ここでは倍数の性質について考えていきましょう!
倍数の性質
- 2の倍数:偶数
- 3の倍数:各位の和が3の倍数 (258、444、711など)
- 4の倍数:下2桁が4の倍数 (100、3844、921756など)
- 5の倍数:下1桁が0か5
- 6の倍数:偶数であり、各位の和が3の倍数 (456、1032など)
- 8の倍数:下3桁が8の倍数 (1000、76440、24168など)
- 9の倍数:各位の和が9の倍数 (111111111、585、369など)
倍数の性質は上の図のようになっております。
これは“必ず覚えておいてください”
これを知っているだけで解ける問題も多いですし、素早く計算に取りかかれます。
さて、これを踏まえて考えると今回は1の位が0か5である必要があります。
問題文に0のカードはないと書かれているので1の位は必ず5になります。
よってボックスの考えと併用すると、初めに入る数は5以外の5通り、
次は4通り、3通り、そして1の位は5の1通りとなります。
よって5×4×3×1=60通りとなります。
気になる方は下の問題で確認してみましょう!意外と楽しいですよ!
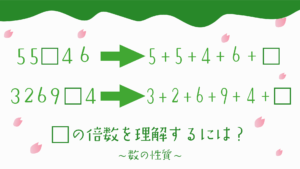

③最後の問題も難しくはありません!!さらっといきましょう。
6けたの整数のうち、下3けたは111と決まっているので、上の3けたを考えましょう。
6つの数字を何回でも使っていいのでそれぞれ6通りの入れ方があります。
よって6×6×6=216通りとなります。
重複する記号の問題も、こちらの問題で復習できますのでぜひ確認してみてくださいね!


[79]問題に挑戦!
答えを見るにはここをクリック!
①24通り
②601通り
[79]解説を見てみよう!
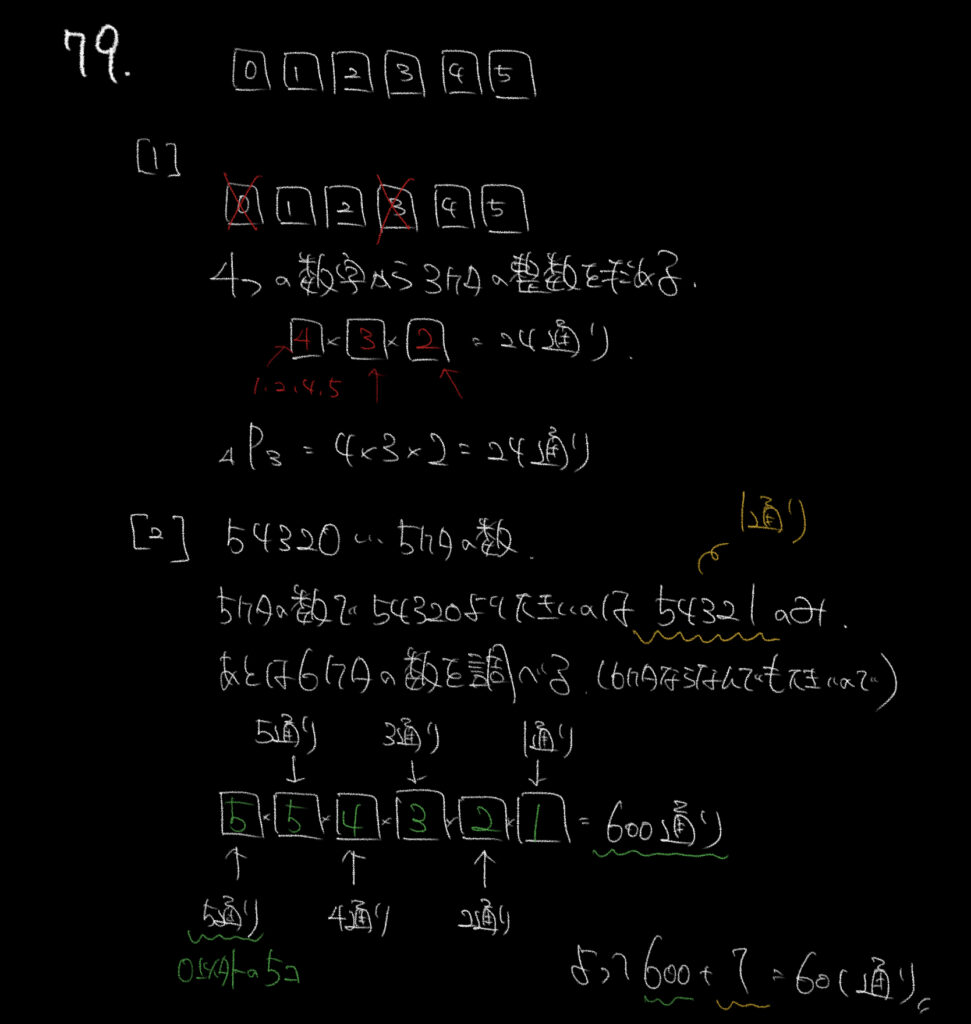
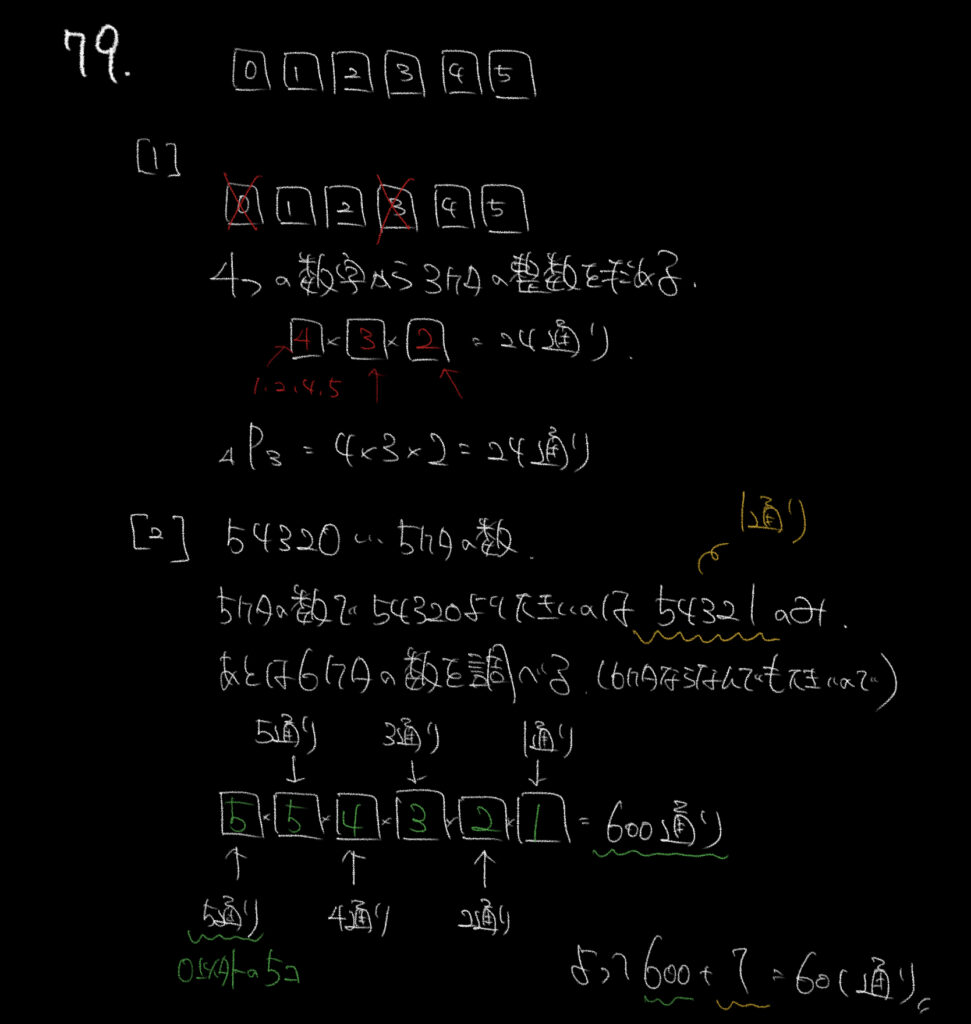
先ほどの問題と少し似ていますが決定的に違う点が一つあります。
それは0のカードがあることです。
一番上の位に0が使えないので数えすぎに注意して解いていきましょう。
①0と3を除く4つの数字から3つの数字を並べます。
ここでは0は使われないので、いつも通りの考えで解いていきましょう。
使える残りの数字は4つなので、4×3×2=24通りです。
②54320よりも多い数を求めたいので今回は5けたの数と6けたの数を考えます。
5けたの数で54320より多いのは54321しかないので1通り。
6けたの数は全て54320よりも大きいので6けたの整数の個数を求めます。
ここで、気をつけたいのが0の存在です。
ボックスの考えを使うと一番上に入る数字は0以外の5通り。
次に入るのは残った4つの数と0を含めた5通り。
あとはいつも通り計算していくと、
5×5×4×3×2×1=600通りとなり、
1+600=601通りとなります。
[80]問題に挑戦!
答えを見るにはここをクリック!
①35通り
②29通り
[80]解説を見てみよう!


今回もボックスをかいて考えていきましょう。
頭の中でやるのと、実際にかいて解くのでは全然違います。
めんどくさがらずにかいていきましょう!!
①「表が4回だけ出る」は言い換えれば、
(コインを7回投げるので)7個のボックスの中から、表が出る4回を選ぶことと等しくなります。
これさえ理解していれば、あとはいつも通り計算するだけです。
7C4(7つの中から4つを選ぶ)=7C3(7つの中から選ばない3つを選ぶ)なので、35通りと計算できます。
②やや難しかったのはこちらの問題でした。
5回以上が表のとき、考えられる場合の数は5回表のとき、6回表のとき、7回全部表のとき、です。
これは2回裏が出る、1回裏が出る、0回裏が出るとも言えるので
計算のカンタンなそっちを計算で求めていきましょう。
解き方は①のやり方と同じです!
すると21+7+1=29通りとなります。


[81]問題に挑戦!
答えを見るにはここをクリック!
①15通り
②15通り
③36通り
[81]解説を見てみよう!




今回の問題は2パターンの解法で解くことができました。
1つ目は①のように地道に調べ上げていくやり方です。
①のようにそこまで時間がかからないものなら、それでもいいかもしれません。
とにかく考えられる組み合わせを抜け漏れがないように書いていきましょう!
下手に計算して落としてしまうのももったいないですしね(笑)
ですが、問題によっては調べられないくらいめんどくさいのもあります。
それが②でした。
②4つの出た目がPQRSの順で小さくなるのは、
PQRSのすべての場合の数の24分の1です。
この考えは、以前にも出てきたのを覚えているでしょうか?


[77]の解説にもかいた通り、出た目がすべて違う場合のPQRSの4人の並び方は24通り以外ありえません。
実際に数字を入れて確かめてみてもわかりますが、
PQRSの数字が1〜6で同じ数字が使えないとき、
並び順は必ずこの24パターンのどれかになります。
よってPQRSの数字が1〜6で同じ数字が使えないときの並び方/24(4人の並び方)で
P,Q,R,Sの順に小さくなっていくような組み合わせを求めることができます。
このやり方をマスターすれば、調べるよりも素早く問題を解くことができます!
③PQが同じになる可能性は1-1、2-2、3-3、4-4、5-5、6-6の6通りあります。
同じようにRSが同じになる場合の数も6通りありますので、6×6=36通りとなります。
まとめ
さて、いかがでしたでしょうか。
以上がカード、コイン、サイコロの単元でした!
困ったらボックスを書くことで攻略していくことが大切でしたね。
問題を解く上で基本となる考えですが、この類の問題では特に
頭の中で計算するのではなく、必ず紙に書くようにしましょう。
お絵かきが大事です!!








