はじめに
みなさんおはようございます!!
通過算の問題では、旅人算のように電車がすれ違うような問題が出ています。
受験生のみなさんが電車に乗っているときも、たまに反対方向からくる電車とすれ違いますよね?
今回はそんな電車のすれ違いに問題に挑戦していきましょう。
まずはいつも通り、問題を解くためのヒントを勉強していきます!
列車が通過するときのヒント
列車が通過するまでの流れを確認しましょう!
列車が通過し始める前
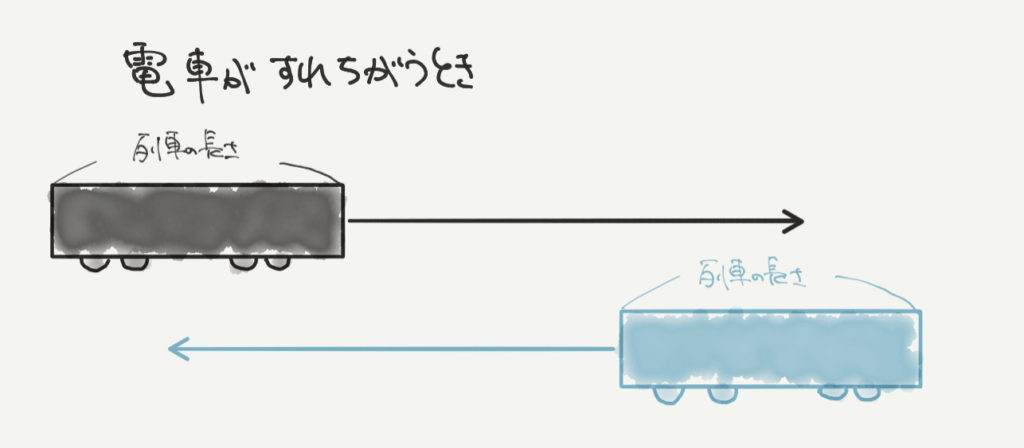
列車が通過し始める前です。
このときはすれ違っていないのでまだ何も始まっていませんね。
列車が通過し始めた瞬間
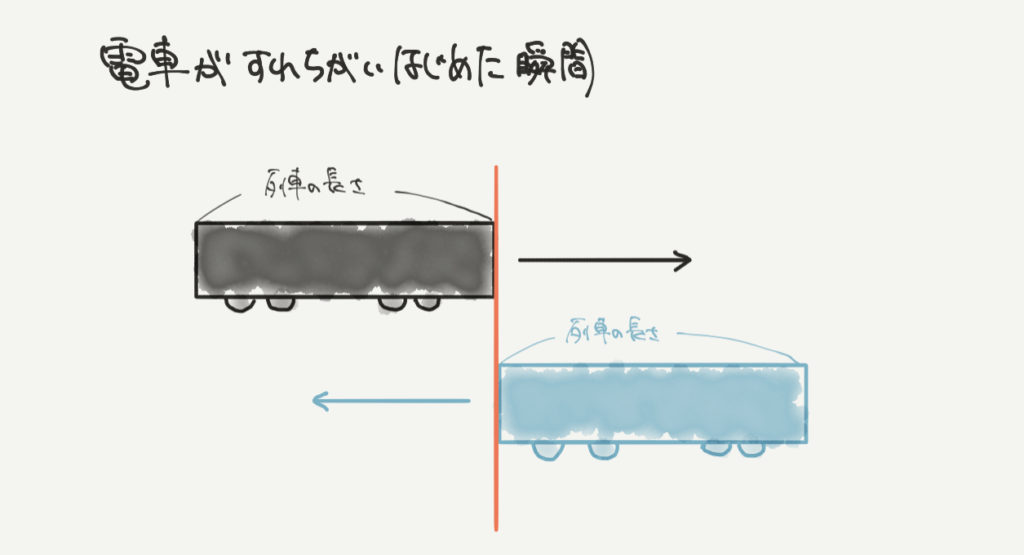
こちらは電車がすれ違い始めたときです。
青色と黒色の列車の先頭同士がすれ違い始めていますね。
問題文で「電車がすれ違い始めてから〜」と言われたらこの瞬間から考えるようにしましょう。
列車が通過している最中
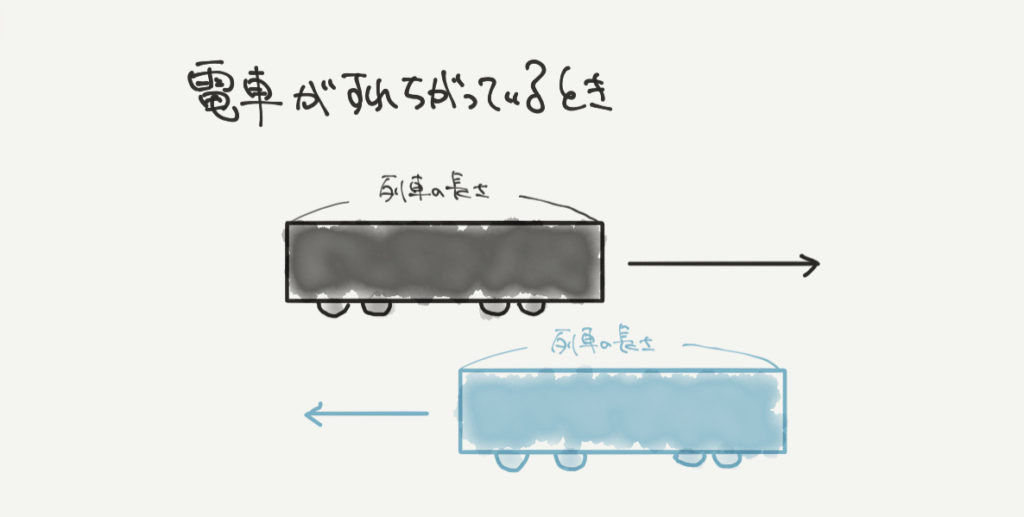
こちらは2つの電車がすれ違っている最中のときです。
特に言うことはなし!!
列車が通過し終わった瞬間
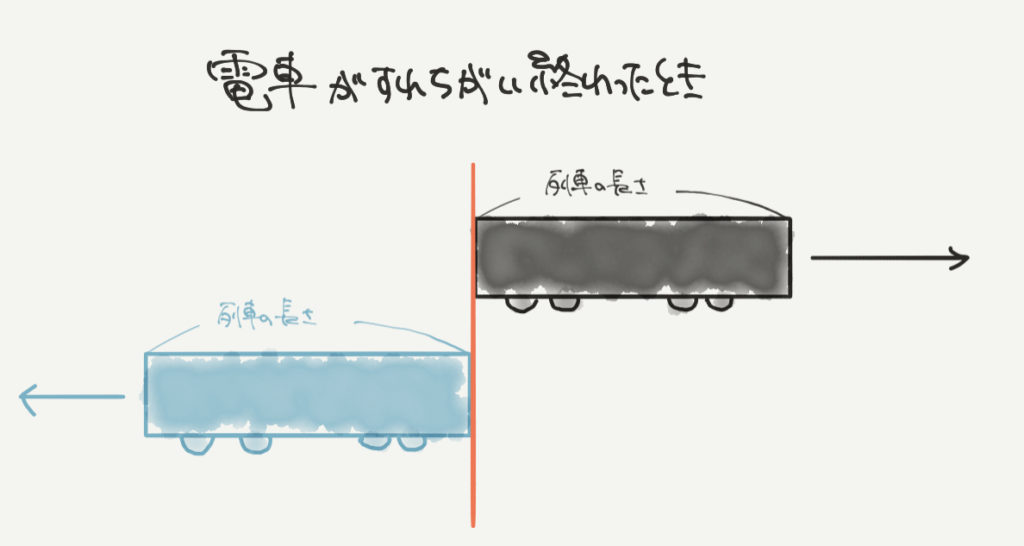
さて、こちらが2つの電車がすれ違い終わるときの絵です。
こちらでは列車の後ろに注目しましょう。
すれ違い終わるのは2つの列車の後ろがすれ違うまでです。
ここまでは通過算、列車がすれ違うときのヒントでした。
このヒントを頭に入れて問題を解いていきましょう〜。
問題に挑戦!
解答
答えを見るにはここをクリック!
3秒
この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略
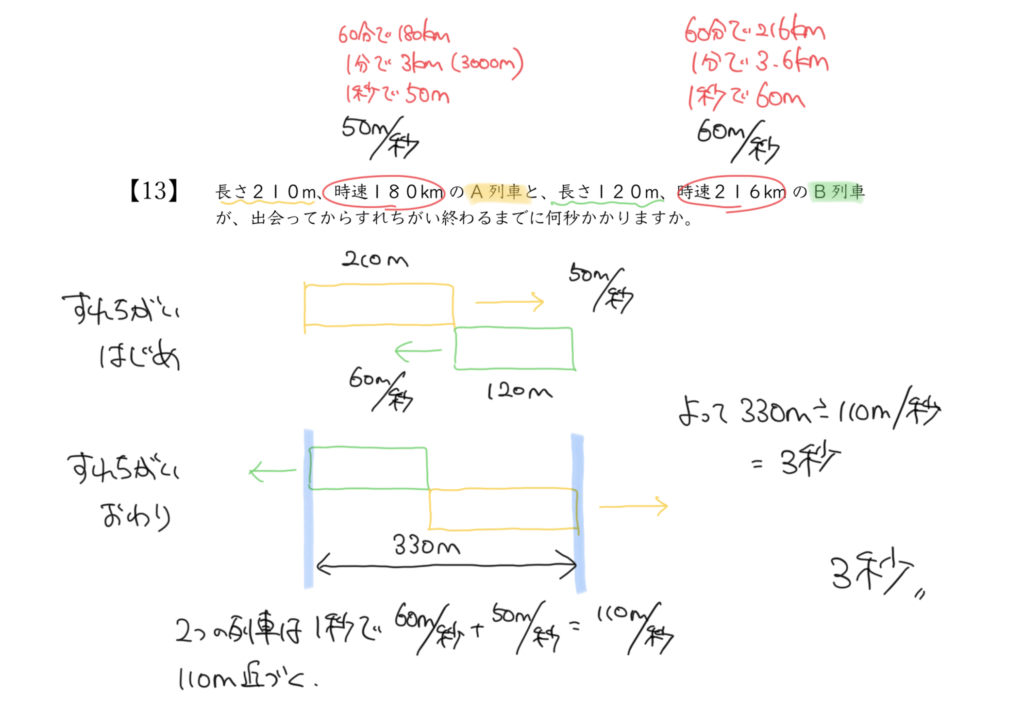
STEP1:それぞれの列車の秒速を求めよう
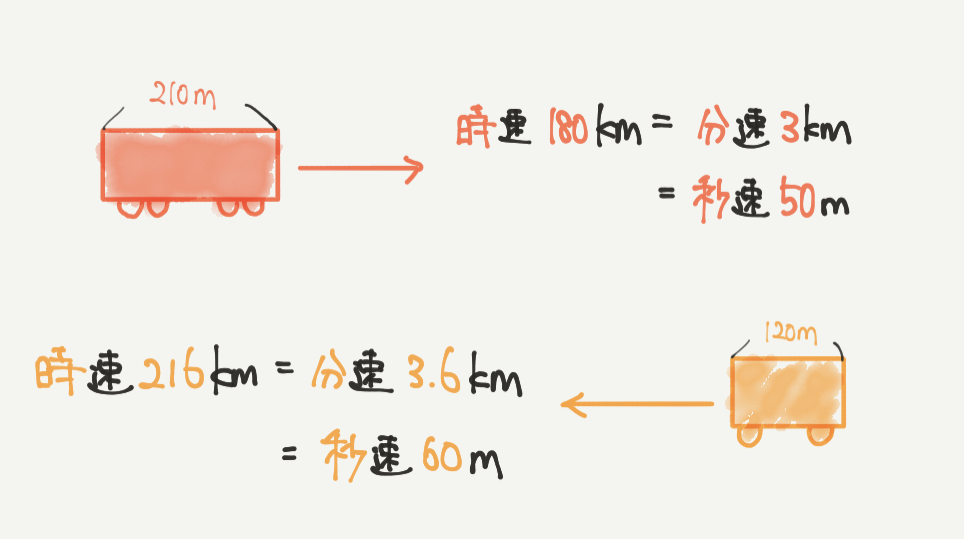
まずは速さの単位をそろえるところから始めていきます。
↑STEP2「問題文を先に図にしよう」から解いても大丈夫です!
赤い列車の秒速を求めよう
時速180kmですので、1時間で180km進むことになります。
1時間で180km
60分で180km
1分で180km÷60分=3km/分(1分間で3km走ることがわかります。)
1分間で3km
60秒で3km
1秒で3km(3000m)÷60秒=50m/秒(1秒で50m進むことがわかります。)
よって赤い列車の秒速は50mです。
黄色い列車の秒速を求めよう
続いて黄色い列車の秒速を計算していきましょう。
時速216kmですので、1時間で216km進むことになります。
1時間で216km
60分で216km
1分で216km÷60分=3.6km/分(1分間で3.6km走ることがわかります。)
1分間で3.6km
60秒で3.6km
1秒で3.6km(3600m)÷60秒=60m/秒(1秒で60m進むことがわかります。)
よって黄色い列車の秒速は60mです。
STEP2:問題文を図にしよう
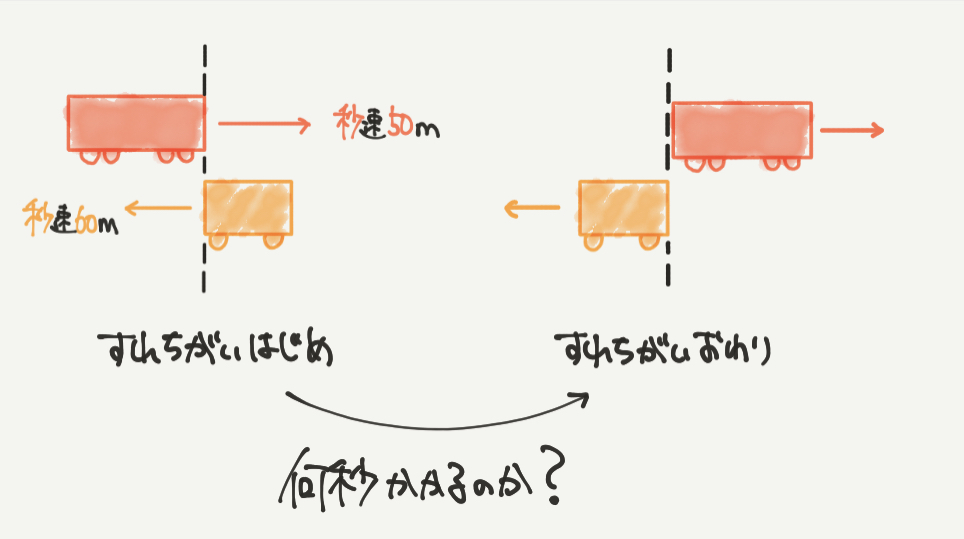
さて、続いては問題文を図にしていきましょう。
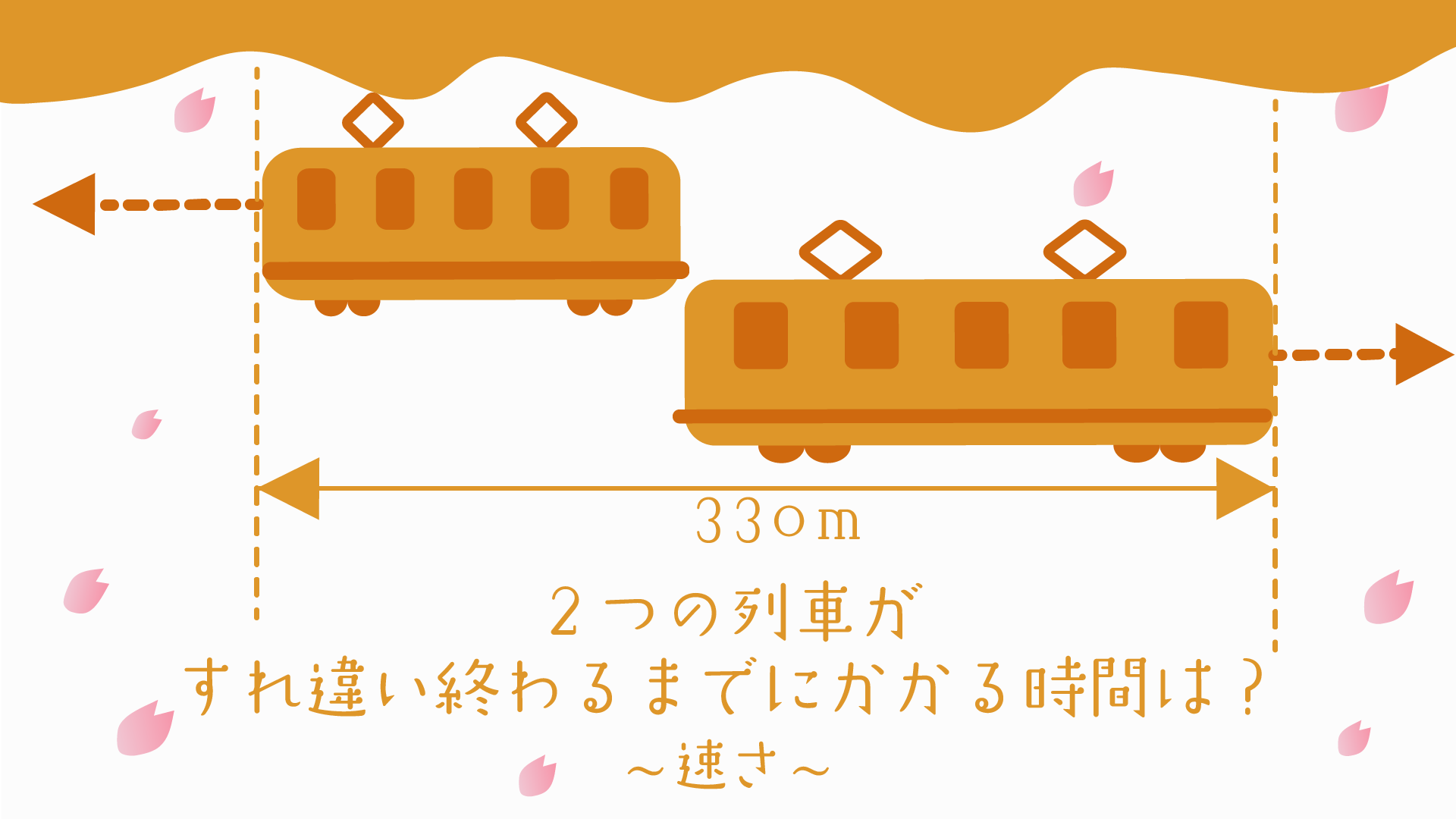
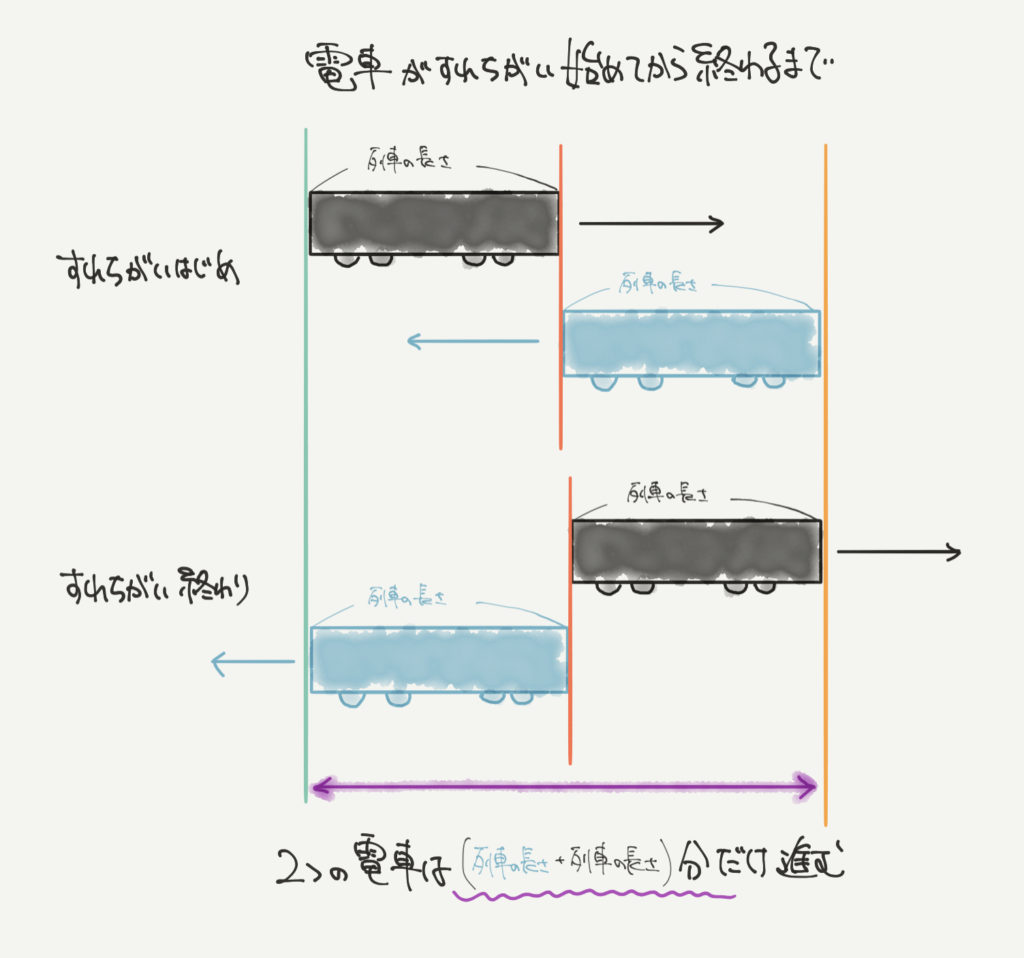
列車がすれ違い始めてから、すれ違い終わるまでを図にしてみました。
こちらをきちんと頭の中に入れてから、STEP3の計算に進みましょう。
STEP3:2つの列車はすれ違うまでにどれくらい進むのか
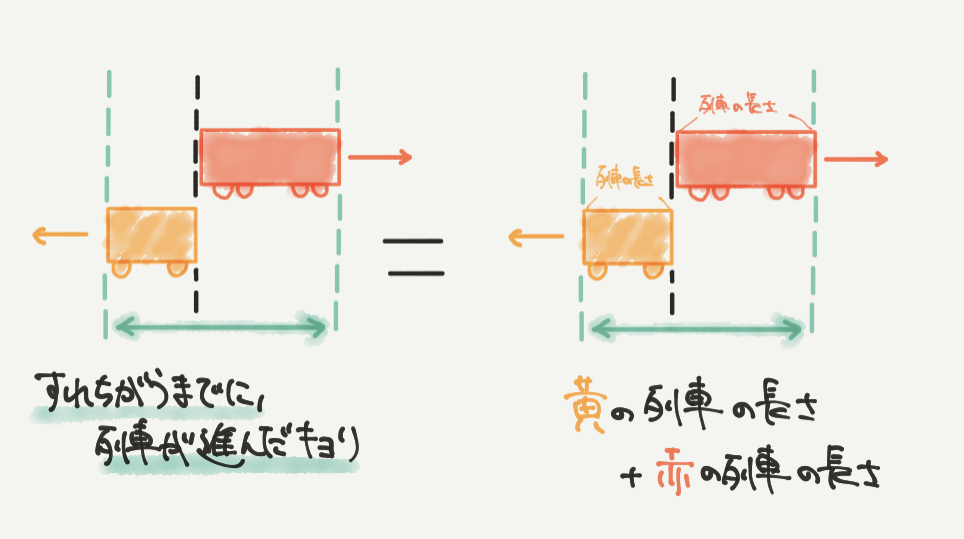
2つの列車がすれ違うまでに進む距離は、黄色の列車の長さ+赤色の列車の長さになります。
また、この2つの列車は反対方向に進んでいるので1秒でかなり遠ざかります。
実際にどれくらい遠ざかるのか、STEP4で計算して求めていきましょう。
STEP4:すれ違うまでの時間を求めよう
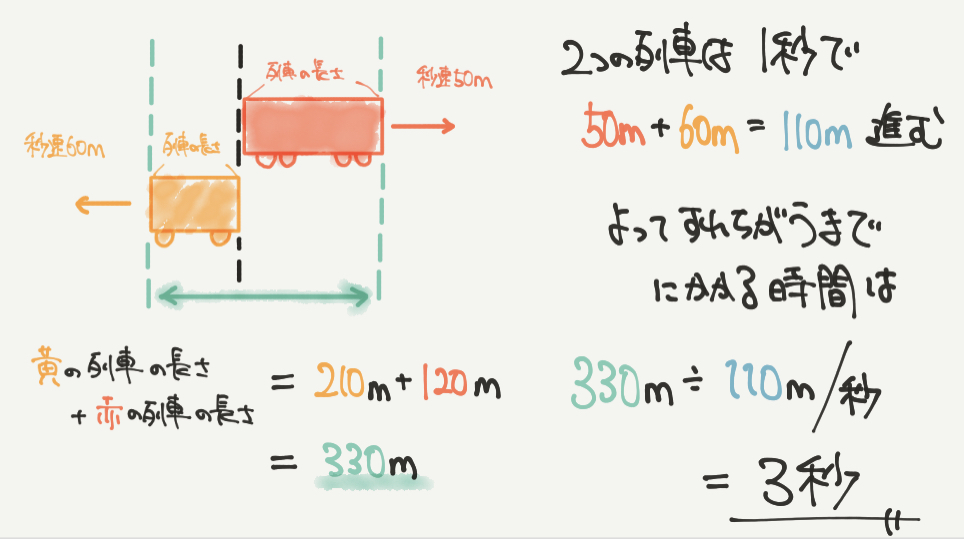
赤の列車は秒速50m、黄色の列車秒速60mで反対方向に進むので、
50m/秒+60m/秒=110m/秒、となり
この列車は1秒間で110m遠ざかることになります。
2つの列車がすれ違うまでに黄色の列車の長さ+赤色の列車の長さ分の距離を進むので、
210m+120m=330m進むことになります。
これらの情報から、2つの列車がすれ違うまでに進んだ時間を
330m÷110m/秒=3秒と答えが出すことができました。
2つの列車がすれ違い終わるまでにかかる時間を求める問題のまとめ
今回の問題で大事なポイント
答えの単位に合わせて計算すること!(STEP1)
列車がすれ違うときの考え方(2つの列車はどれくらいの距離を進むのか?)
2つの列車が1秒間で遠ざかる距離はいくつか?(旅人算の復習)
この問題で大切だったことは、
①答えの単位に合わせて計算する(STEP1:単位をmにそろえること!)
②すれ違うときの考え方(2つの列車はどれくらいの距離を進むのか?)
③2つの列車が1秒間で遠ざかる距離はいくつか?(旅人算の復習!)
の3点でした。
特にこの記事では、列車のすれ違いの考え方を重点的に勉強しましたね!
引き続きこの調子でほかの問題にも挑戦していきましょう!