はじめに
みなさんおはようございます!!
本日も通過算の問題にチャレンジしていきましょう。
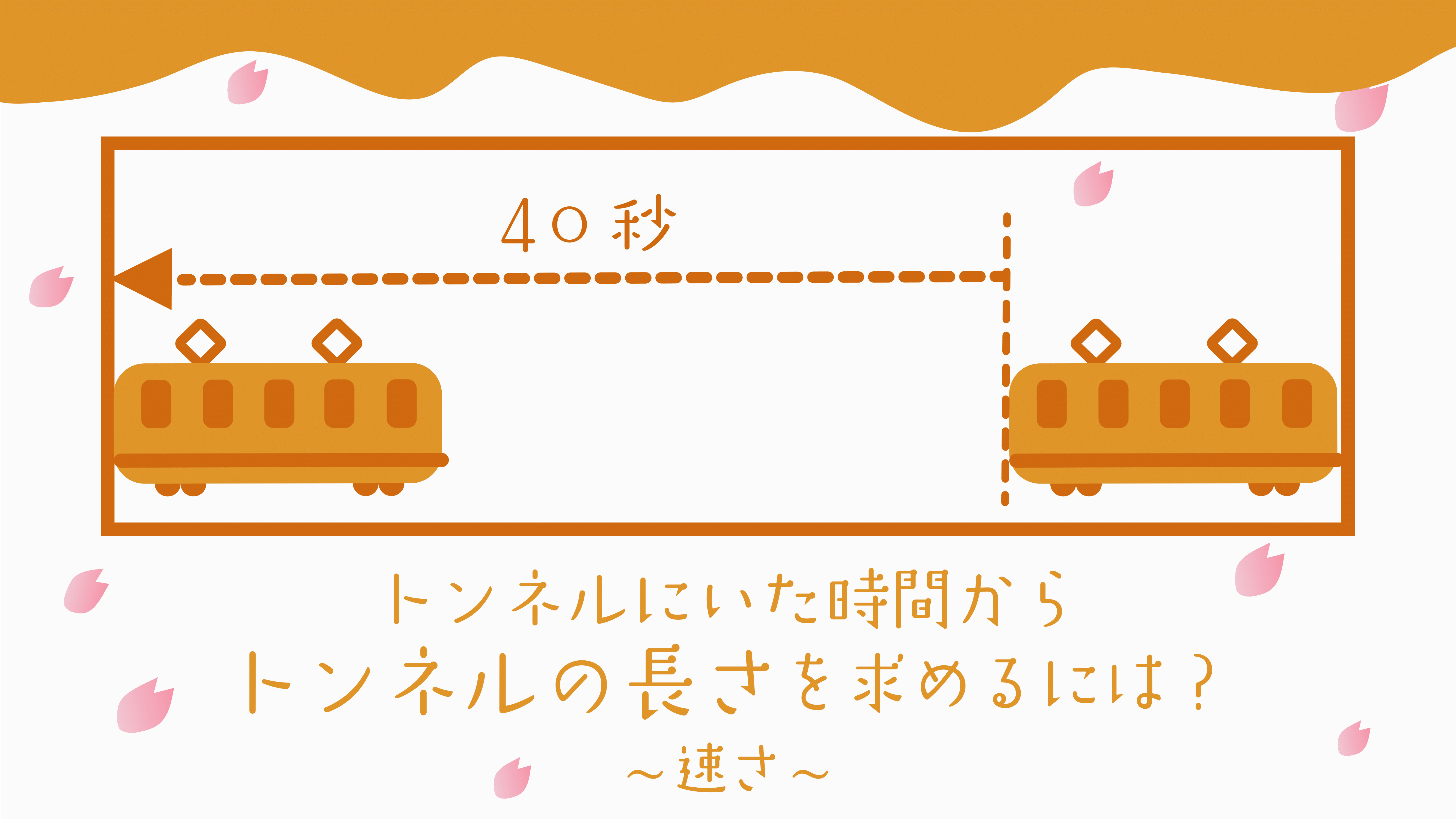
この問題では列車が完全にトンネルの中にかくれている時間から、トンネル全体の長さを求めるような問題です。
まずは通過算の基本的な知識から復習していきましょう!
トンネルの中に列車が完全にかくれているとき
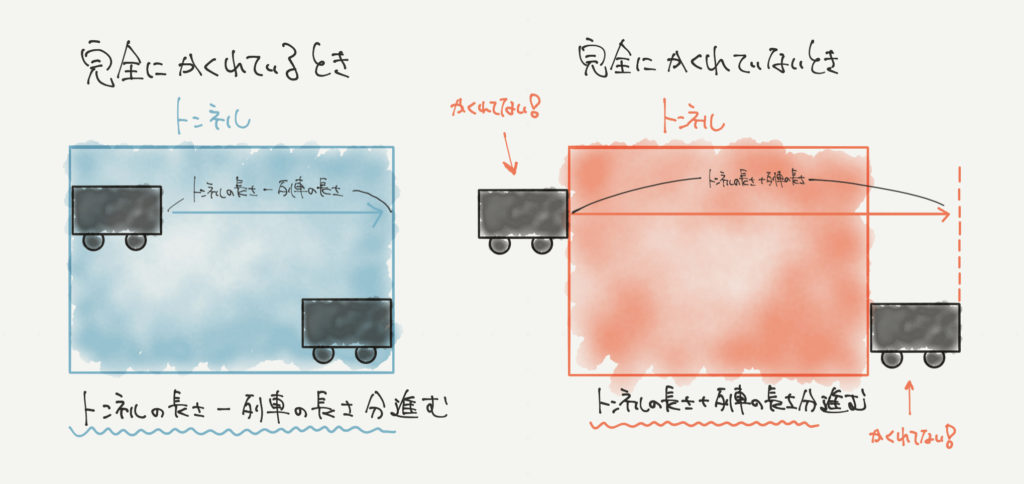
列車が完全にかくれているとき=列車がトンネルに入り終わってから出始めるとき、です!
↑列車がトンネルに入り終わってから出始めるとき→トンネルの長さ–列車の長さ分進みます。
例えば列車が完全にかくれていないとき、赤いトンネルの図にようになります。
電車が入り始めてからですと、電車がまだ完全にかくれていないですね!
また、トンネルから出終わるまでですと電車が見えてしまっているのでかくれていないことになります。
今回のこの問題では、完全にかくれていることに注意して問題を解いていきましょう。
問題に挑戦!
解答
答えを見るにはここをクリック!
660m
この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略
STEP1:時速を秒速になおそう
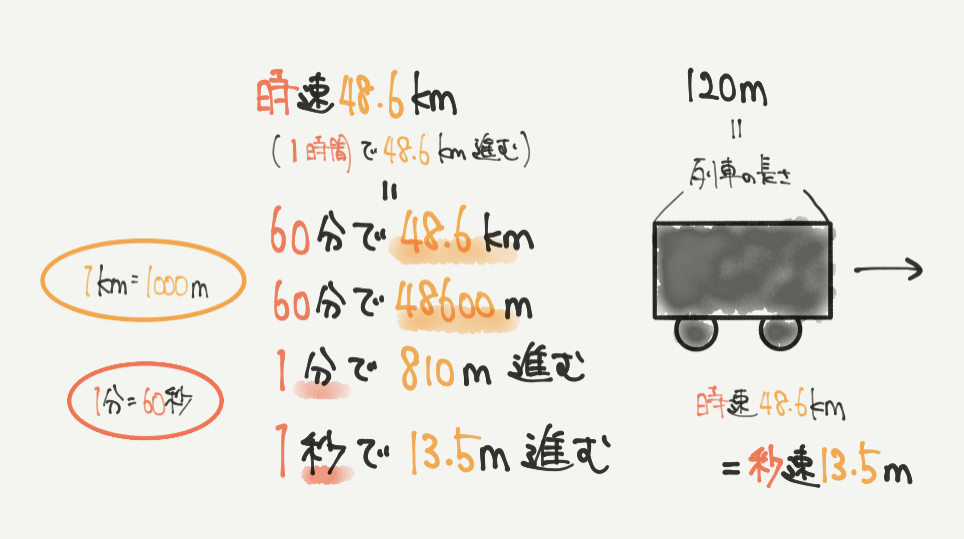
速さの問題では、速さの単位をそろえることが大切です。
今回の問題では答えがトンネルの長さなので、まずは列車の時速を秒速○mになおしていきましょう。
まず時速48.6kmから順番に考えましょう。
時速48.6km=1時間で48.6km進むということなので、
1時間=60分、1km=1000mを使って、
60分で48600m進むというふうに言いかえることができます。
よって1分で進む距離は、
48600m÷60分=810m/分で、810m進むことがわかります。
最後に分速を秒速になおしていきます。
1分(60秒)で810m進みますので、
1秒で進む距離は、
810m÷60秒=13.5m/秒で、13.5m進むこととなります。
ここまでがSTEP1の内容です!!
STEP2:トンネルにかくれているとき、列車はどこからどこまで進む?
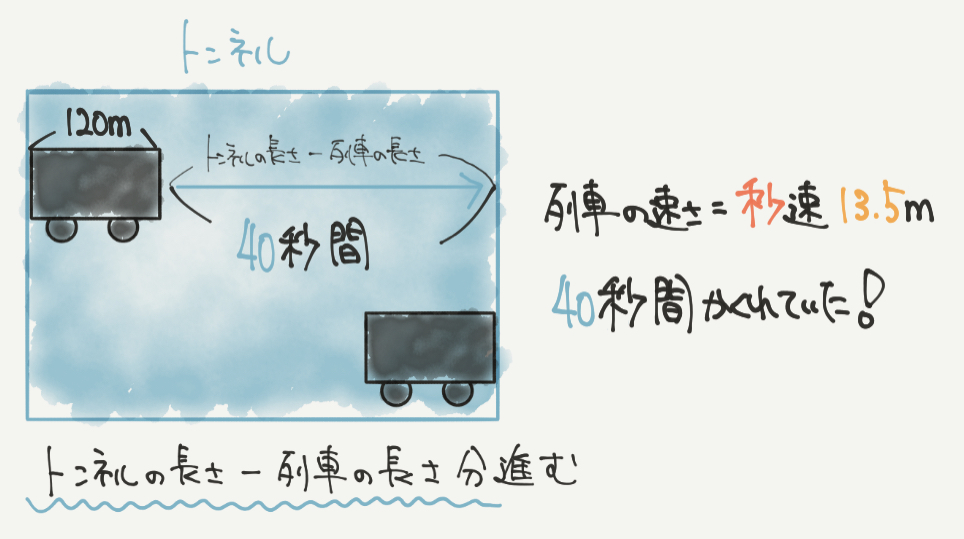
この列車は問題文で「トンネルに40秒間完全にかくれていた」とあるので、
トンネルの長さ→列車の長さ分の距離を40秒で走っていることがわかります。
秒速13.5mで40秒間走ったので、トンネルの長さ→列車の長さ分の距離をSTEP3で計算していきましょう。
STEP3:列車が進んだ距離を計算しよう
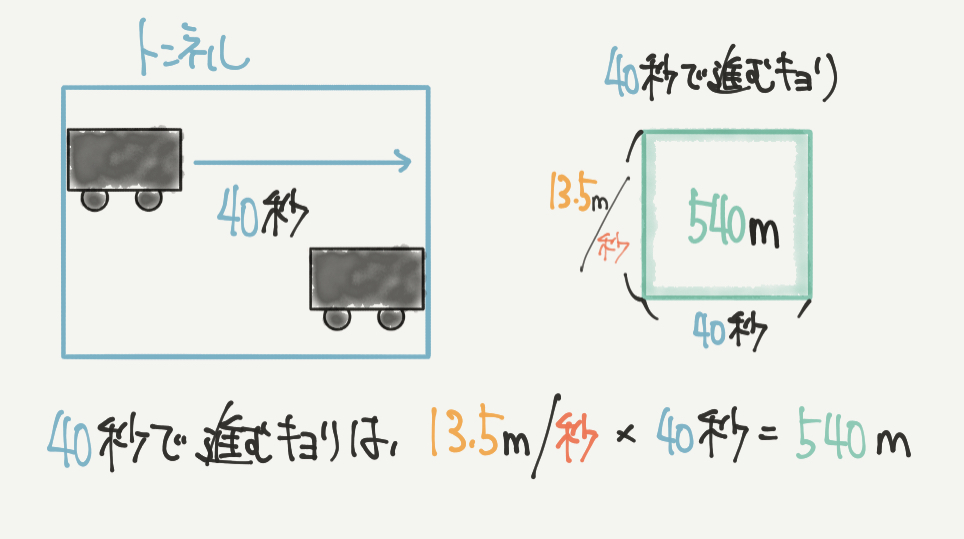
秒速13.5mで40秒間走った距離を面積図を書いて求めていきます。
面積図はたてを速さ、横を時間と書いて計算するととてもわかりやすいです。
よって、今回列車がトンネルにかくれている間に進んだ距離は、
13.5m/秒×40秒=540mとなります。
さあ、あとは答えを求めるだけです!
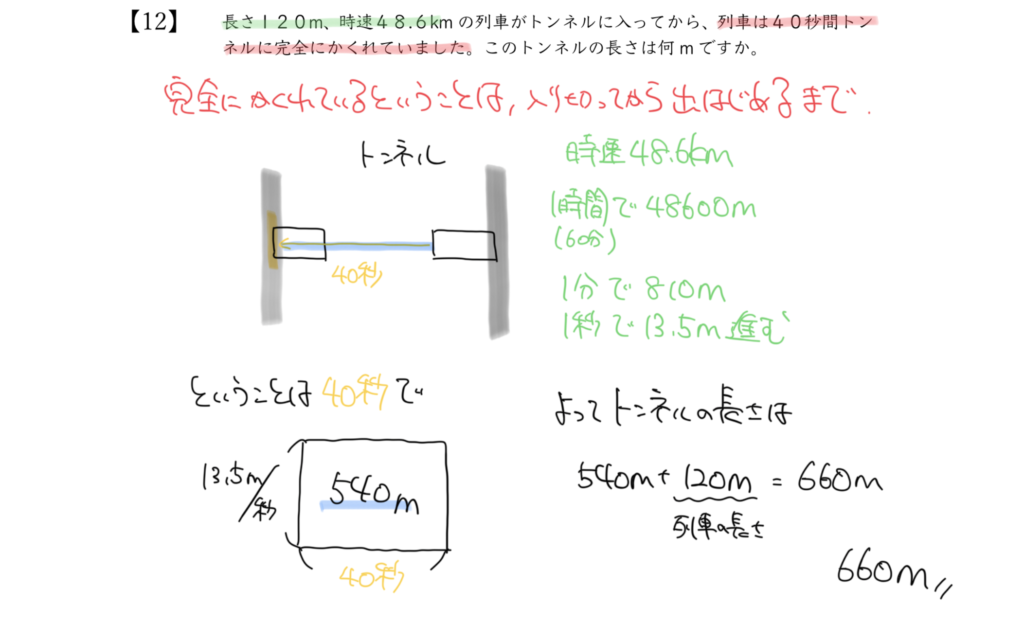
STEP4:求めたい答えはトンネルの長さ
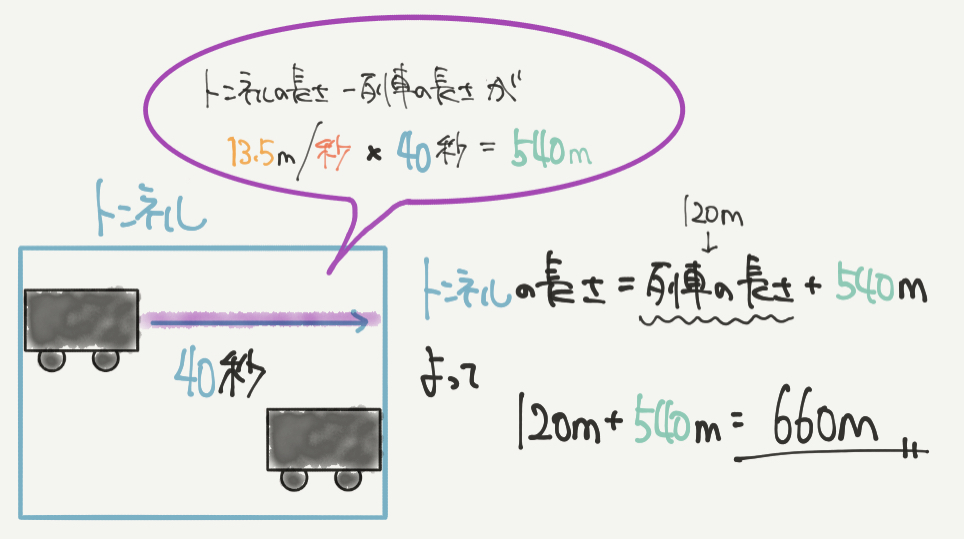
気をつけてほしいのは答え(トンネルの長さ)が540mではないことです!
STEP3まで計算しても、きちんと図を書いていないとケアレスミスしてしまいます。
今回知りたいトンネルの長さは、
540m+列車の長さで求めることができますので
トンネルの長さは540m+120m=660mと答えを出すことができました。
トンネルにいた時間からトンネルの長さを求める問題のまとめ
今回の問題で大事なポイント
速さの単位をそろえよう
・今回の答えの単位は「m」なので、「m」でそろえよう!
トンネルに完全に隠れているときの考え方(STEP2、3、4)
・列車は「トンネルの長さ–列車の長さ」の距離だけ進む
今回の問題で重要だったポイントは、
①答えから問題文の単位を同じにする考え方(単位をそろえる)
②トンネルに完全にかくれているときに列車が進む距離(トンネルの長さ–列車の長さ分進む!)
の2つの点でした。
ほかの通過算の問題や速さの問題でも、問題文に注意することや、
速さの単位を同じにそろえる考え方は大事になります。
ほかの通過算の問題にもぜひ挑戦しておきましょう!