はじめに
みなさんこんばんは!!
今回解く問題は「流水算」に関する問題です。
「さんすうがく」ではじめて勉強する受験生にもわかるようにていねいに解説していますので、一緒にがんばっていきましょう。
流水算の復習から!
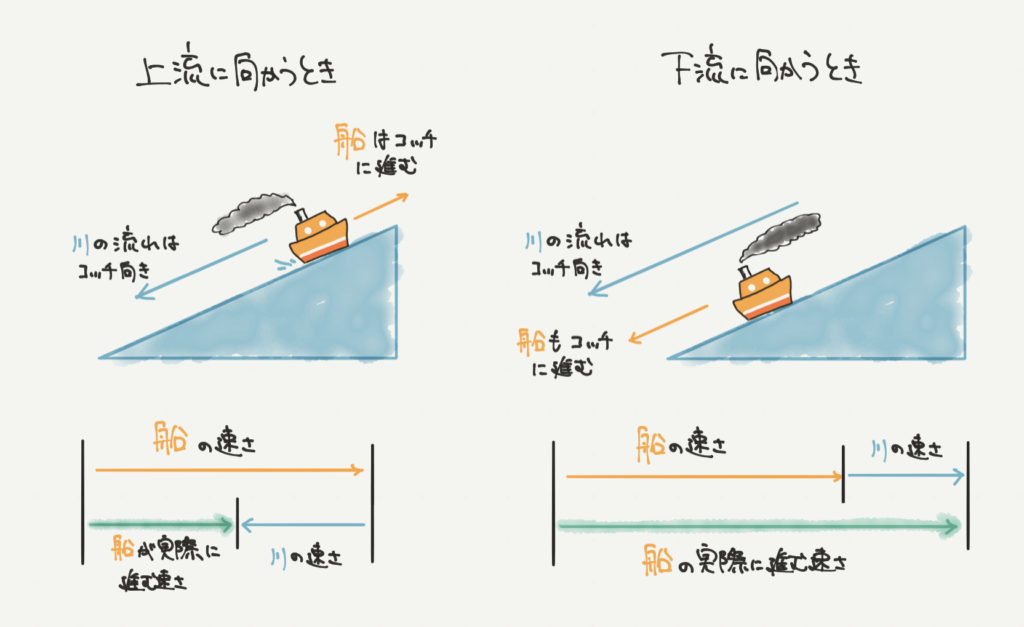
流水算では、上(上流)と下(下流)に向かう場合で船の速さが変わります。
たとえば、船が上流に向かって進むとき船の速さは少し遅くなります。
このときの船の速さは船のもとの速さ–川の速さで求めることができます。
逆に船が下流に向かって進むとき船の速さは少しはやくなります。
この場合、船の速さは船のもとの速さ+川の速さで求められます。
以上が流水算の基本でした。
このポイントをおさえながら、問題に挑戦していきましょう!
問題に挑戦!
解答
答えを見るにはここをクリック!
4km/時
この記事を書いている人はこんな人


解説を読んで「 速さ 」を攻略
STEP1:速さの線分図を理解しよう
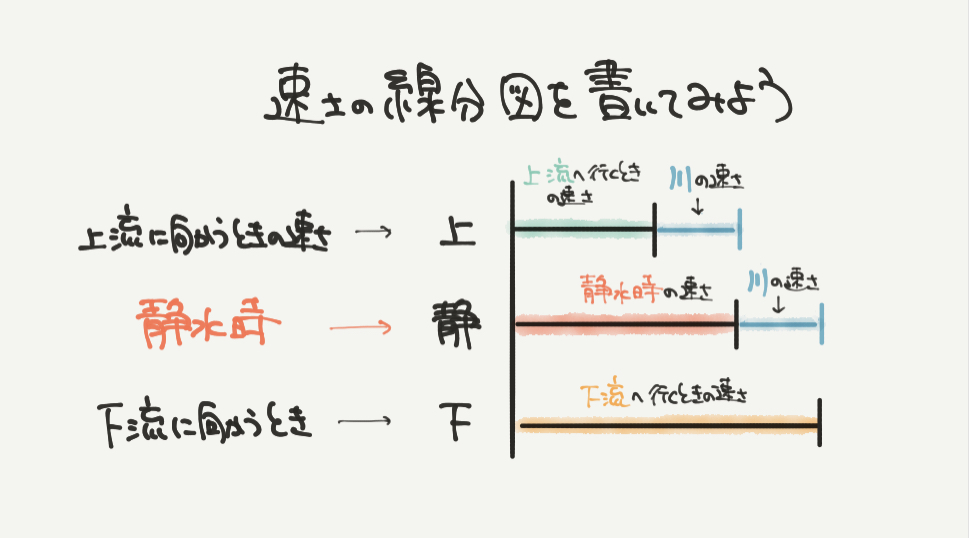
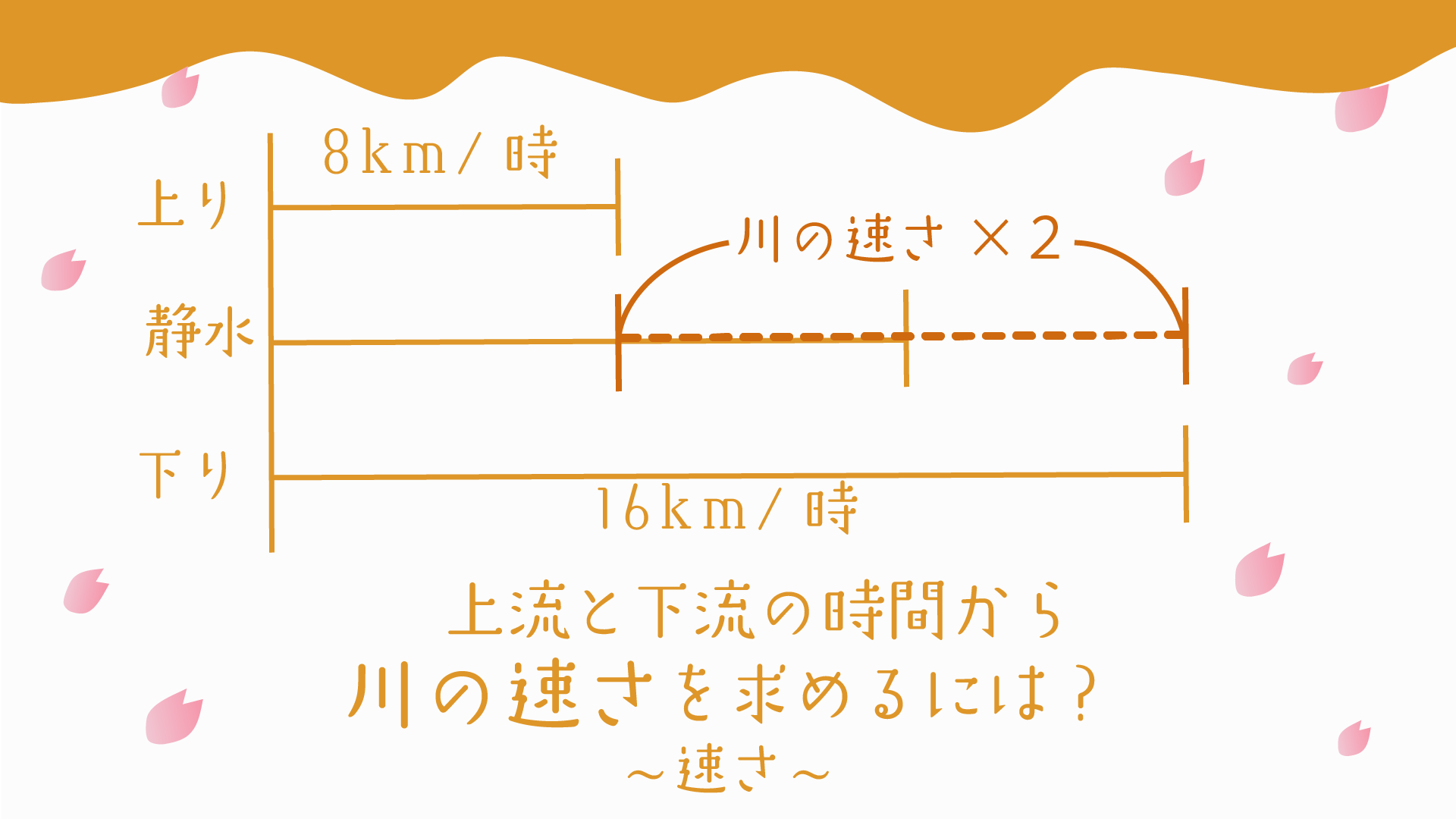
まずは流水算で重要な速さの線分図について確認しておきましょう。
流水算では速さがコロコロ変わります。
なので、上流に向かうときの速さ、静水時のときの速さ、
下流に向かうときの速さの3つの線分図を書いて求めていきます。
そしてポイントになるのが、川の速さです。
静水時の速さと上流へ向かうときの速さの差と、
静水時の速さと下流へ向かうときの速さの差が川の速さになります。
STEP2:問題文の内容を図にしよう
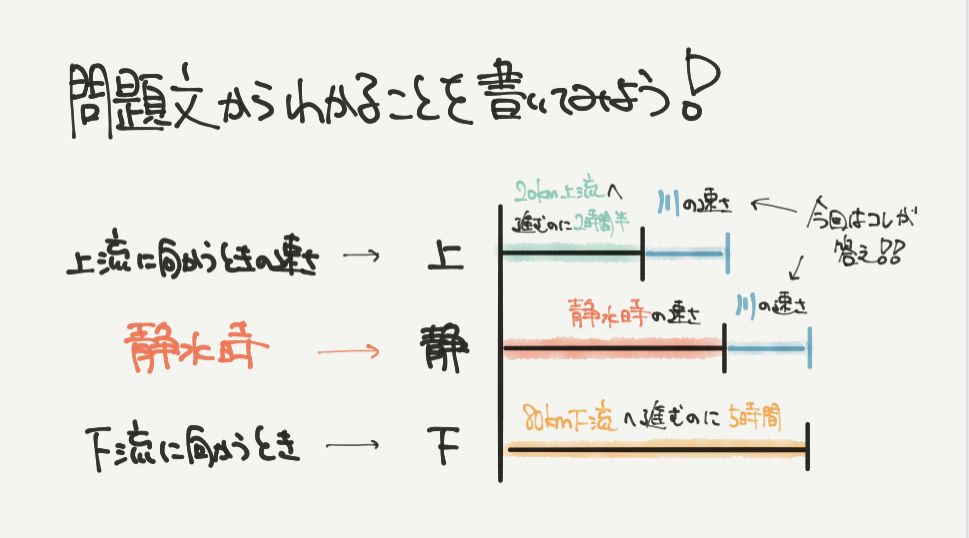
STEP2では問題分の内容を図にしていきましょう。
今回問題文では、「上流へ向かうときの速さ」「下流に向かうときの速さ」に関する2つの情報があります。
問題文から読み取れる情報
上流に向かうときの速さ:20km進むのに2時間半かかった。
下流に向かうときの速さ:80km進むのに5時間かかった。
これらの情報を使ってSTEP3で計算していきましょう。
STEP3:上流、下流に進むときの速さを求めよう
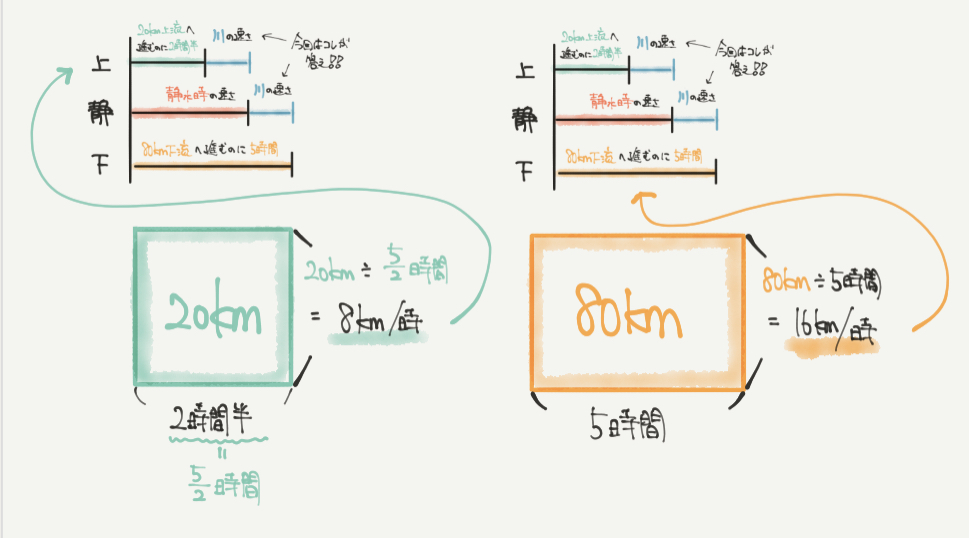
上流に進むときの速さ
上流に向かうときの速さは20km進むのに2時間半かかったので、
20km÷5/2時間=8km/時と求められます。
下流に進むときの速さ
下流に向かうときの速さは80km進むのに5時間かかったので、
80km÷5時間=16km/時と計算できます。
STEP4:最後は川の速さを計算しよう
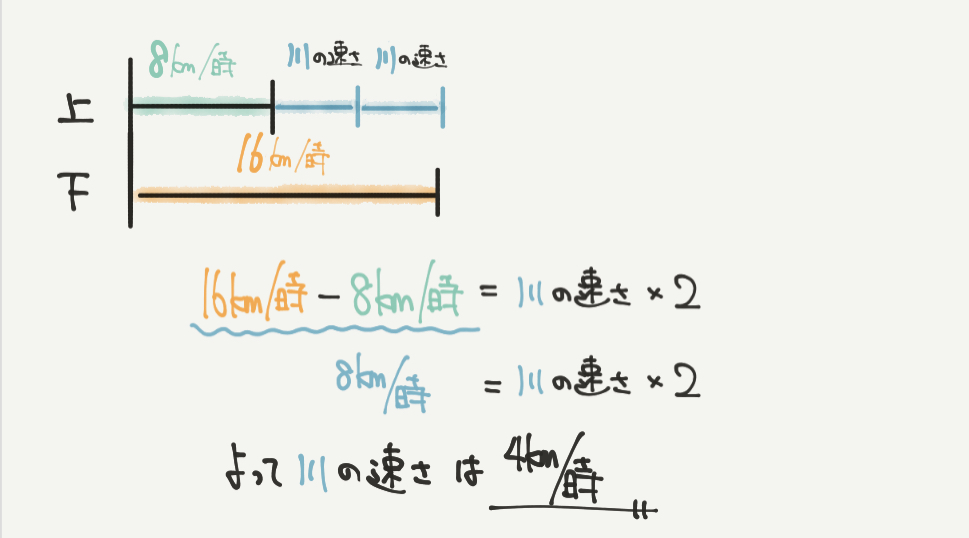
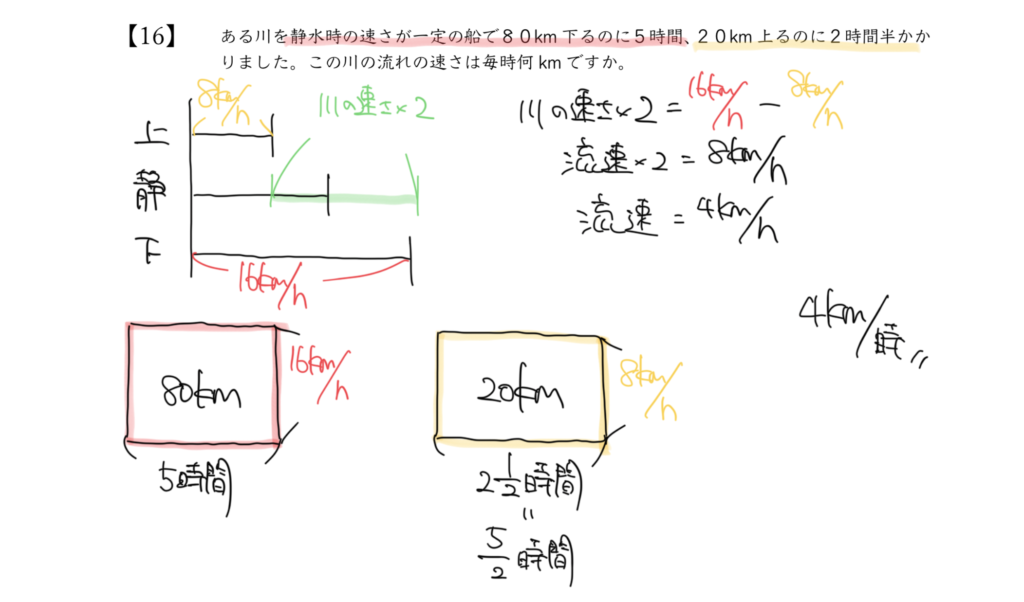
STEP3で求めた8km/時と16km/時を速さの線分図に書きこんでいきましょう。
速さの線分図から、上流に向かうときの速さと下流に向かうときの速さの差が、川の速さ×2となります。
よって、
16km/時–8km/時=8km/時(川の速さ2個分)なので
川の速さは、
8km/時÷2=4km/時と求めることができました。
上流と下流まで進む時間から川の速さを求める問題のまとめ
今回の問題で大事なポイント
流水算の考え方(速さがコロコロ変わる!!)
・速さの線分図(STEP1)
・速さの面積図(STEP3)
速さの考え方(速さの単位をそろえよう)
以上が今回の流水算の問題でした!!
よくがんばりました!!
この問題では速さの線分図が超重要になってくるような問題でしたね。
頭の中計算してしまうとこんがらがってしまったり、わからなくなってしまいます。
なので少し時間をかけても、速さの線分図をきちんと書くようにしていきましょう!
ほかにも流水算の問題はたくさんありますので、速さの線分図を今のうちにカンペキにしておきましょう。