【中学受験算数】流水算は川の速さが大事！面積図を書いて川の上流に向かって進む時にかかる時間を計算してみよう！

はじめに

みなさんこんばんは！！
今日は中学受験に出てくる速さの問題、「流水算」と呼よばれる問題です！

1からていねいに解説していますので、はじめて解く受験生は下のヒントから勉強していきましょう。
それではいきますよ〜！

流水算の超基本ちょうきほん！！

流水算で大事なのは川の速さ

流水算の問題では、川の流れがポイントになってきます。
まずはその川の流れについてのかんたんな解説です。
川は雨が降ふることによってできます。

山に雨が降り、その雨が集まって川になります。
ここで覚えておいて欲しいのは、川は上から下に向かって流れているということです。

この川の上の部分を上流じょうりゅう、下の部分を下流かりゅうと言います。
流水算の問題ではこれらの知識ちしきを頭に入れておきましょう。

速さの線分図を書いておこう

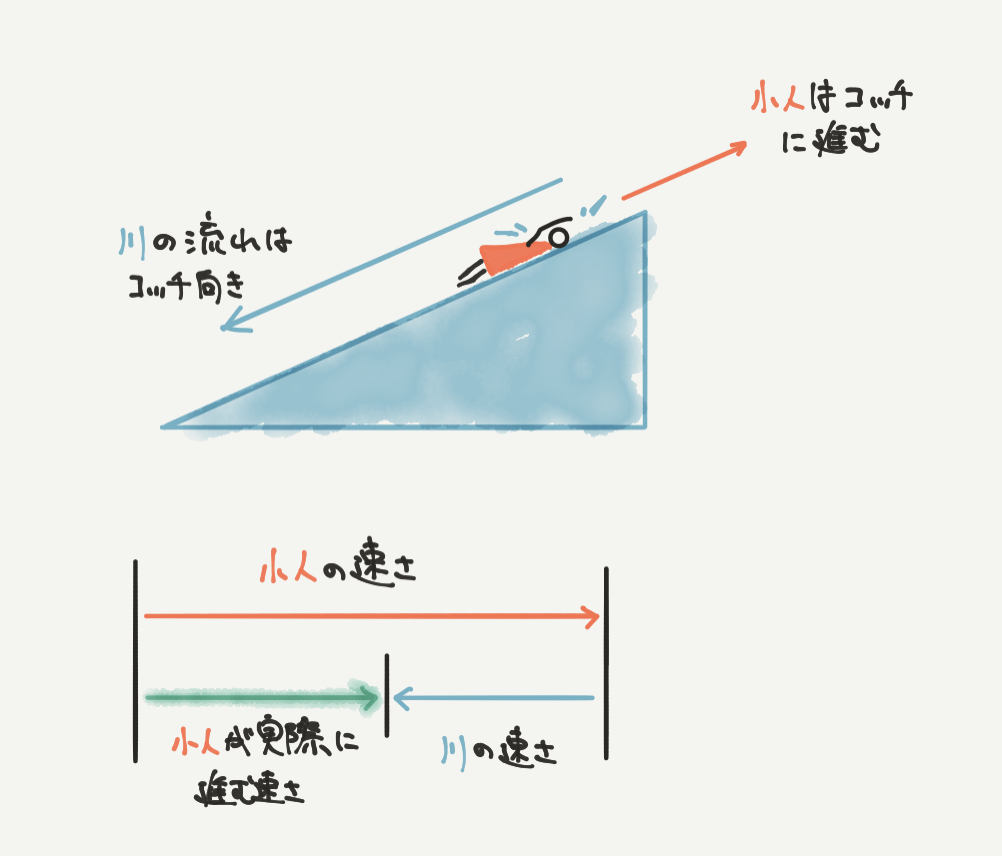
流水算の問題では、速さがコロコロと変わります。
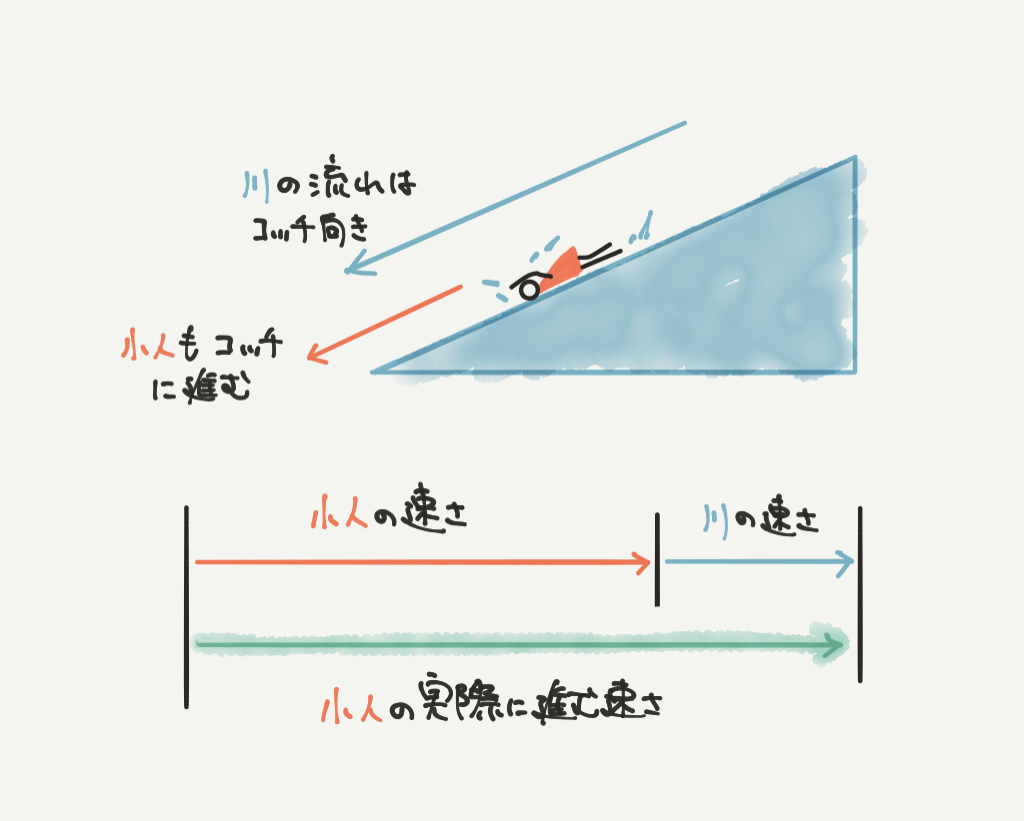
たとえば、上の図では赤い小人が川の上流じょうりゅうに向かって泳いでいます。

このとき赤い小人の実際じっさいに進む速さは、
小人の速さ-川の速さとなります！

こちらは赤い小人が下流かりゅうに向かって進むときの図です。

このとき赤い小人の実際じっさいに進む速さは、
小人の速さ＋川の速さとなります！

このように、小人が進む方向によって計算で使う速さが変わってきますので注意しましょう！
それではさっそく問題に挑戦ちょうせんです。

問題に挑戦ちょうせん！

プールで毎分75mの速さで泳ぐ人が、毎分15mの速さで流れる川の上流に向かって120m泳ぐには、何分かかりますか。

解答

この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略こうりゃく

STEP1：問題文から静水時せいすいじの速さをとらえよう

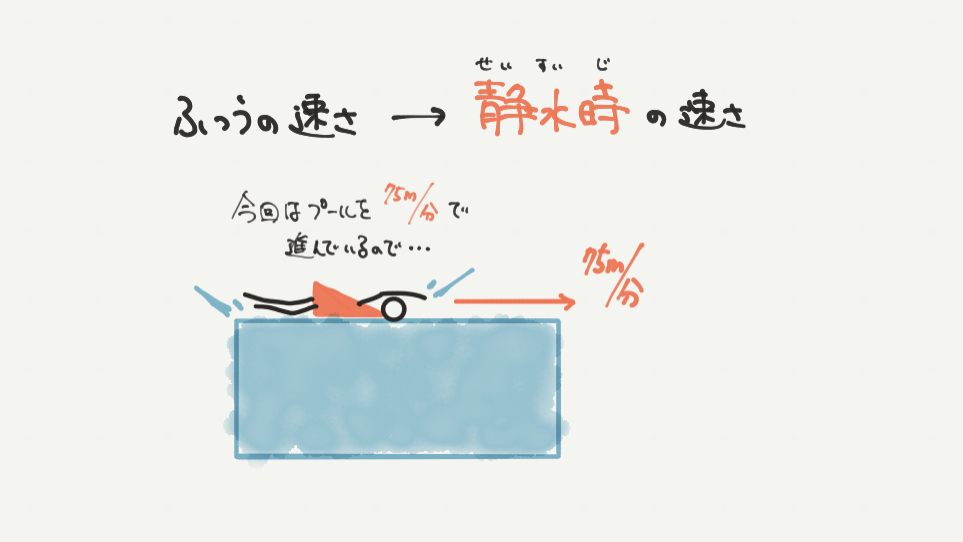
まずは問題文からふつうの速さ（川の流れを考えない速さ）を求めましょう。
ちなみにこのふつうの速さを静水時せいすいじの速さといいます。

静水時せいすいじとは漢字の通り、水が静かな時なので川の流れを考えない速さとなります。
今回は問題文で、プールを進むときの速さが75m/分とわかります。

STEP2：上流に向かうときの速さを求めよう

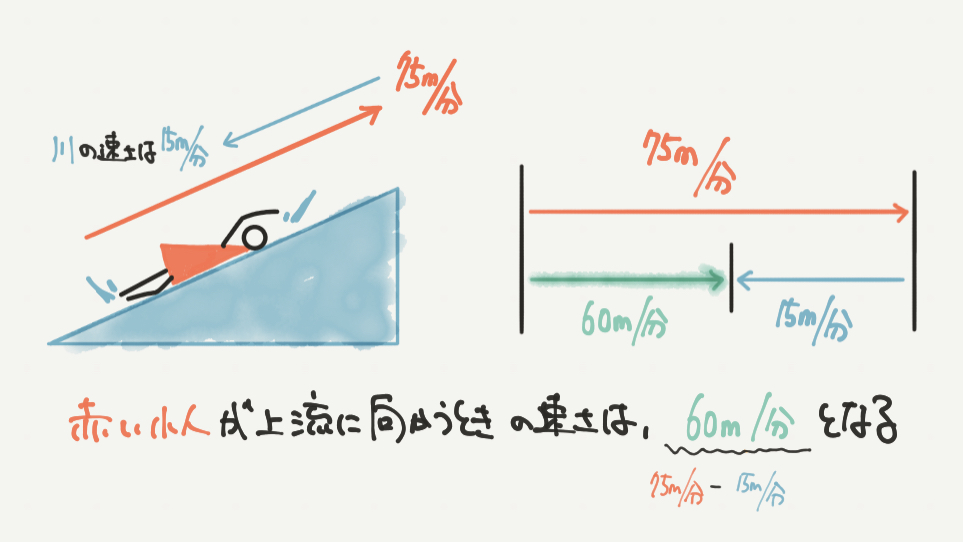
さて、STEP1では静水時せいすいじのときの速さ（75m/分）を求めました。
STEP2では赤い小人が上流じょうりゅうに向かうときの速さを求めてみましょう。

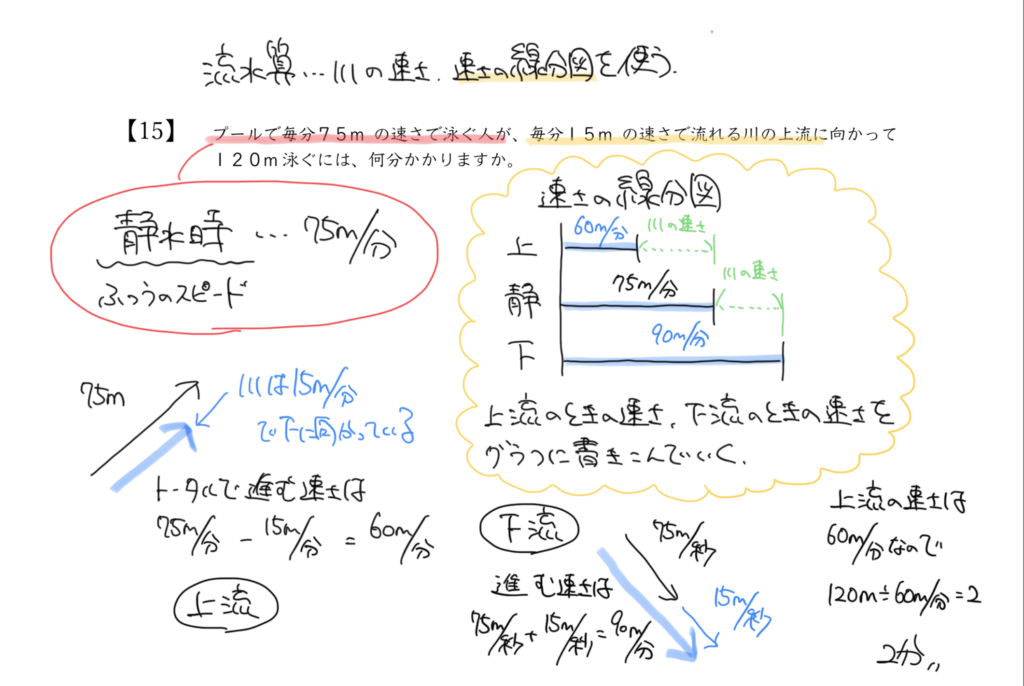
まずは左の図から、上流へ向かうときの速さが75m/分よりも遅おそくなっていることがわかります。
次に右図の線分図より、上流に向かうときの正確せいかくな速さを求めましょう。

今回は線分図を使って、75m/分–15m/分＝60m/分と計算できます。

STEP3：速さの線分図を書いてみよう

STEP2で上流へ進むときの速さを60m/分と求めることができましたね。
STEP3は今回はやってもやらなくても問題は解けます。

ですがこの先もっとむずかしい流水算の問題を解くときに、
とても大切になってくる考え方ですので、ぜひ確認しましょう。

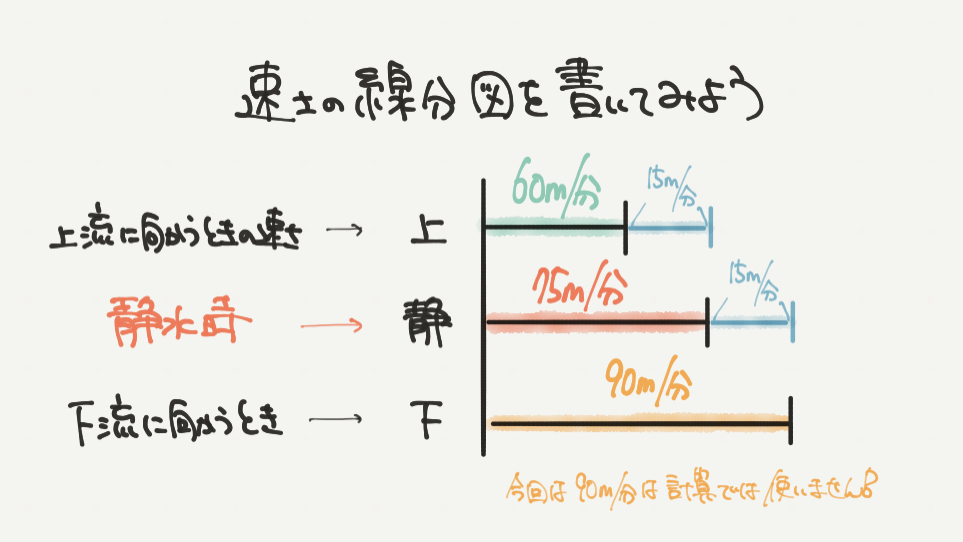
流水算では上図のように、速さの線分図を書くことがとても大事です。
書き方は上から「上流じょうりゅうに向かうときに速さ」、「静水時せいすいじのときの速さ」、「下流かりゅうに向かうときの速さ」です。

↑今回は「下流かりゅうに向かうときの速さ」を求める必要はないですが、90m/分と計算することができます。

この図を書いておくことで、ケアレスミスをしないように考えることができるんです！

STEP4：最後は計算して120m上流に進むまでの時間を求めよう！

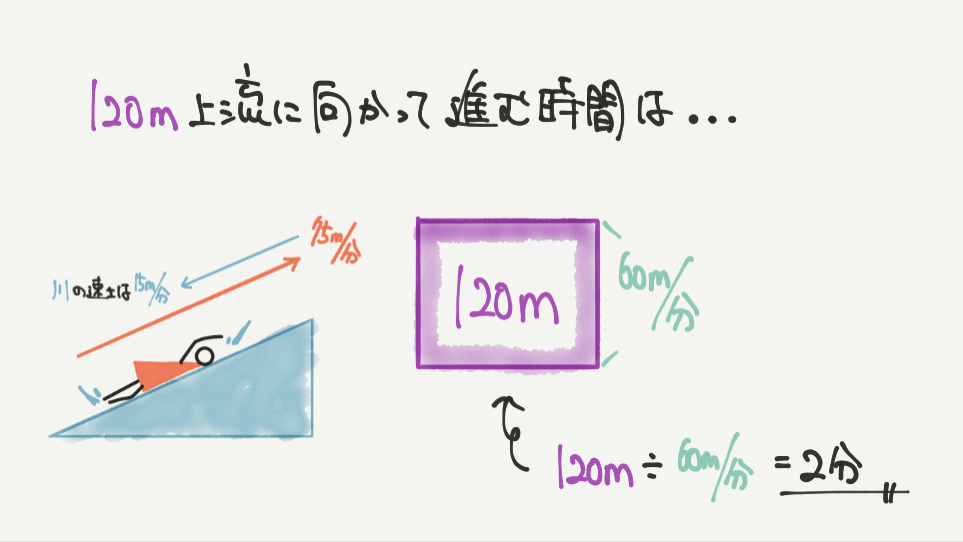
さあ、最後は計算をするだけです。
120m上流に向かって、60m/分で進みますので、速さの面積図を書きながら計算していきましょう。

とくに追加の説明はないです。
120m÷60m/分＝2分と求まりますね！！

川の上流に向かって進む時にかかる時間を求める問題のまとめ

以上で、今回の問題はおしまいです。
流水算の基礎中きそちゅうの基礎きその問題でした。

今回の問題で大事なポイント

流水算の考え方（速さがコロコロ変わる！！）
・静水時せいすいじはふつうの速さのこと（STEP1）
・速さの線分図（STEP3）
速さの面積図（STEP4）

この問題で大切な点は↑の3点でした。
速さの問題のなかでも流水算は苦手とする人が多いと思います。

なのでいつもよりもていねいにSTEPを確認しながら解いていきましょう。
またSTEP3でもやりましたが、速さの線分図は書いたことがない受験生も多いと思うので
今のうちからしっかり練習しておきましょう。

それではもう少しむずかしい、流水算にチャレンジしていきましょう〜！！！

その他の単元の問題の復習はこちらから！