【中学受験算数】「割合と比」を線分図を書いて解きまくろう！！AとBの持っている土地の面積比から始めの2人土地の面積を求めるにはどんな線分図を書けばいい？

はじめに

みなさんこんばんは！！
気がついたらもう夜中の12時になってしまいました。

今日も中学受験算数の「割合と比」に関する問題にチャレンジしていきましょう！
はじめてこの「さんすうがく」をみている受験生も、すぐにわかるようにていねいに解説を書いていますので、
一緒にがんばっていきましょう〜！

今日の問題とそっくりな問題がこちら！！

品物２つの比の変化から値段を求めるには？

まず今日の問題を解く前におさらいしておきたいのが上の問題です！
この上の記事の問題を勉強してから問題を解くと、より今日の解説が分かりやすくなると思うので、

時間がある受験生はまずこちらから確認してみてくださいね！
それでは今日の問題を解いていきましょう！

〈プロ講師のみ〉数学が苦手な生徒のための個別塾「数強塾」

問題に挑戦ちょうせんしよう！

A、B２人の持っている土地の面積の比は3:1でしたが、Aは150㎡を売り、Bは200㎡を買ったので、AとBの土地の面積の比は3:2になりました。2人がはじめに持っていた土地の面積はそれぞれ何㎡ですか。

解答

この記事を書いている人はこんな人

解説を読んで「 割合と比 」を攻略こうりゃくしよう！

STEP1：問題文を線分図にしよう

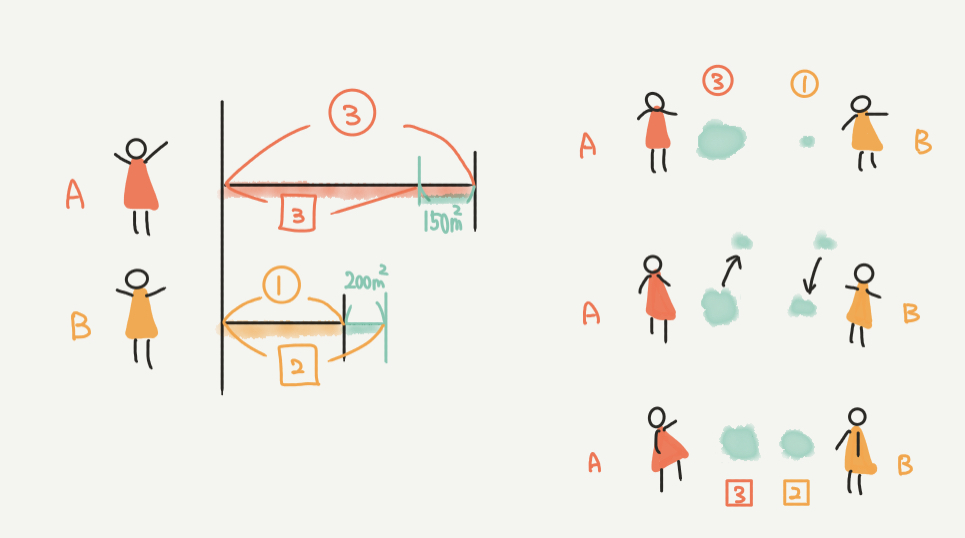
まずは問題文の内容を図するところから始めていきましょう！
線分図が左、絵にすると右になります。

線分図をかくときの注意点は、記号を同じものでかかないようにすることです。
↑今回は○の数字がもともと持っていた土地が基準きじゅんで、□が土地の面積が変化した後の土地が基準きじゅんになっています。

STEP1のこの図をきちんとかければ、あとは計算するだけです。
なのでまずはこの線分図を確実にかけるように練習しましょう！！！

STEP2：同じところがない！なら作ろう！！

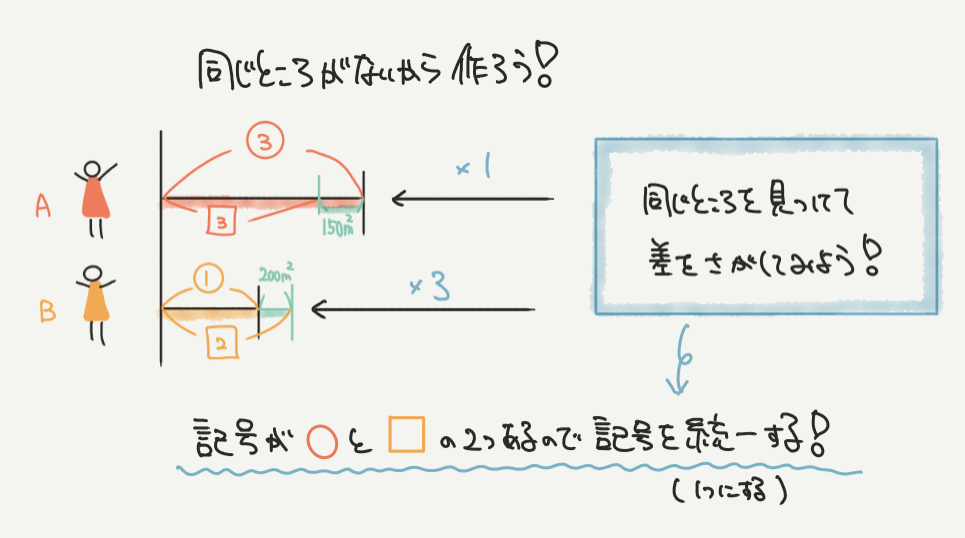
この図から、わかるところを探していきましょう。
普通ふつうの問題であれば、同じところを探さがして解いていきますが、この図では同じところがありませんよね？

そういうときは同じところを作ってしまえばいいのです。
たとえば、今回は③と①を同じにしたいので、Aの図を1倍（そのまま）、Bの図を3倍にして見ましょう。

するとAの③が1倍されて③になり、
同じくBも①が3倍されて③になりますね！

どういうことかわからない受験生は、STEP3を見てみてください！

↑これが「同じところを見つける、作る」という算数の大事な考え方になります。

STEP3：同じところを作る

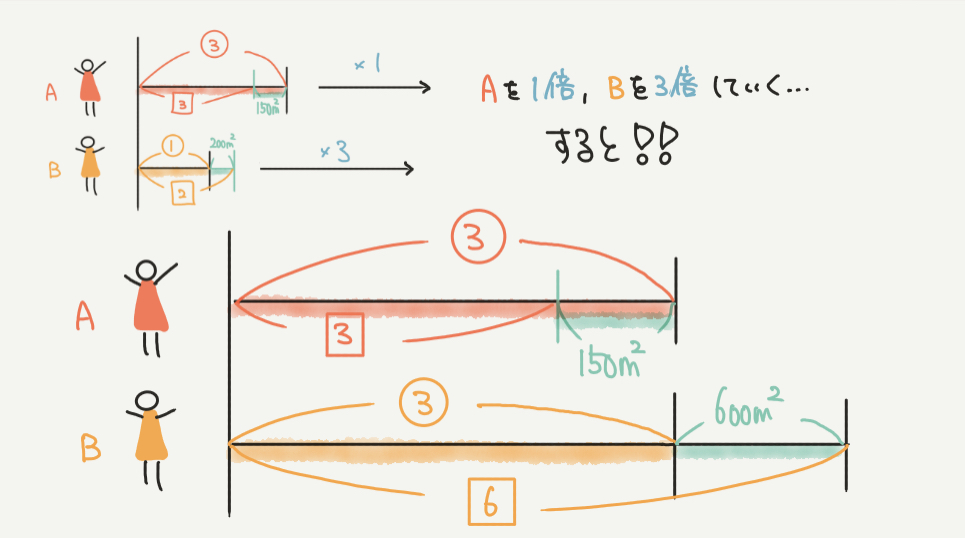
同じところを作ると上の図のようになります。
今回はAの土地③とBの土地①を③にそろえて同じものを作りました。

Aの土地（③）を1倍するということはAの図をそのままにして、
Bの土地（①）は3倍するので、①と200㎡も3倍することになります。

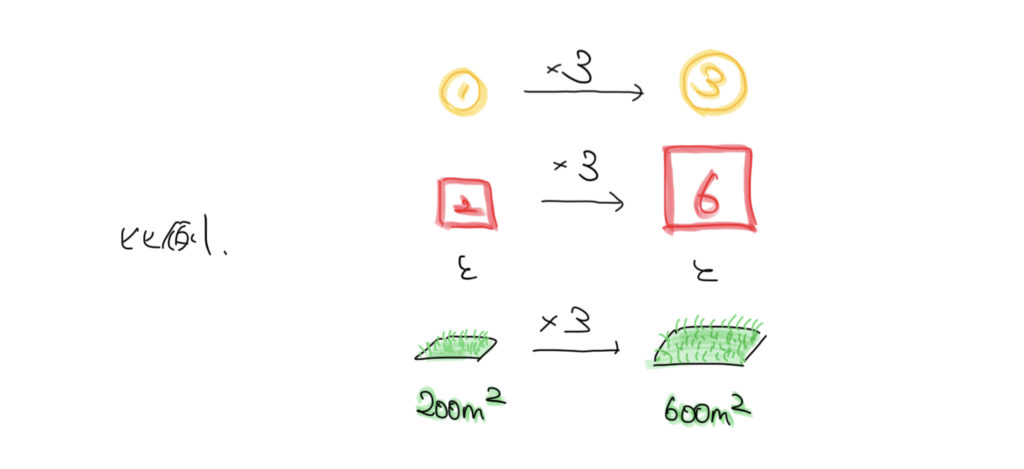
これは比例の復習ですね！

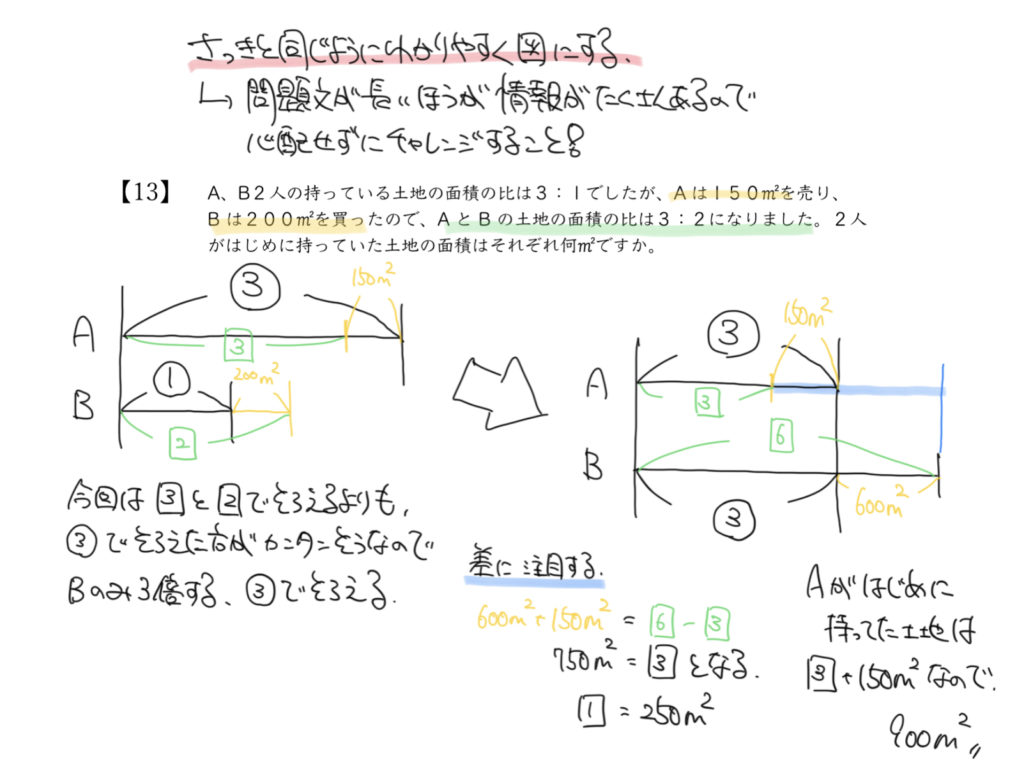
STEP4：同じところから差を見つけて解いていきましょう

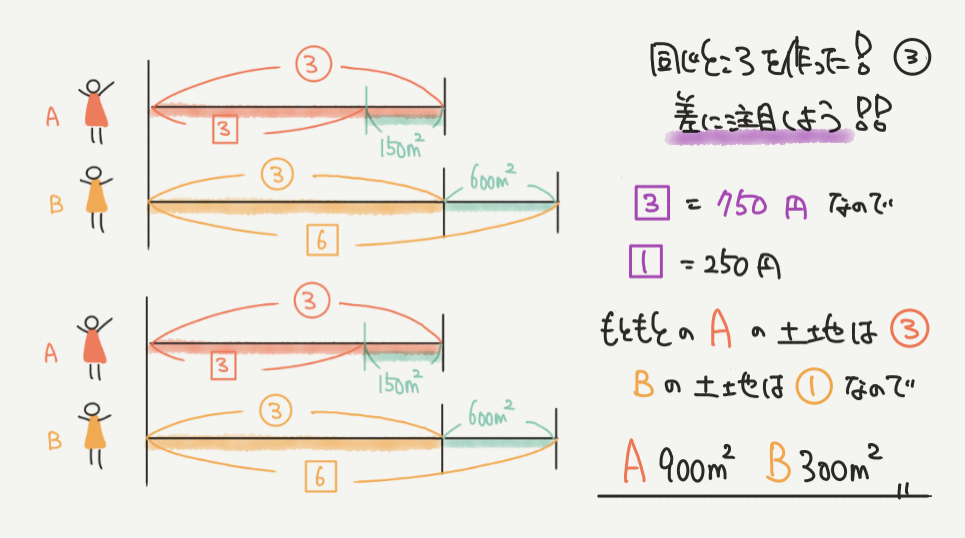
ここでAとBの線分図の部分を③とそろえたことで、
□の6と□の3の差（□の3）が750㎡であることがわかります。

よって、
□の3＝750㎡なので
□の1＝250㎡になります。

答えはもともとのAとBの土地なので、もともとの線分図から答えを求めます。
3倍したBの線分図の答えを答えてはいけませんので、注意してくださいね！！

Aのもとの土地③（□の3+150㎡）なので900㎡、
Bのもとの土地は①なので
900㎡÷3＝300㎡となります！

2人の土地の面積比から始めの土地の面積を求める問題のまとめ

今回の問題で大事なポイント

線分図の書き方（STEP1）
・問題文をきちんと図にする練習をしよう
「同じところを見つける、作る」考え方（STEP2）
・同じところを今回は作ろう！（STEP3）
・比例の考え方を理解しよう！（STEP3）

線分図もそろそろ書き慣なれてきたでしょうか。
1から「さんすうがく」の問題を勉強している受験生は、
もうこのような問題を解けるようになってきていると思います。

しっかりと実力がついてきている証拠しょうこですね！

今回の問題のまとめですが、
①線分図の考え方
②同じところを見つける、作るの考え方
③比例についての考え方
が大事な問題でしたね。

そしてそろえたところ（同じところ）から差に注目することも重要でしたね。
ちなみに今回の問題のように文章が長い問題の方が、正解しやすかったりするのを知っていましたか？

それでは次の問題に進んでいきましょう！！

その他の単元の問題の復習はこちらから！