はじめに
みなさんこんにちは!
それでは今日の問題を見ていきましょう!
今回解く問題は「立体図形」で、複雑な形をしているときの表面積と体積を求める問題です。
前に似た問題を平面図形で一度やっていますね。
「立体図形」の前に平面図形で復習したい受験生は下の記事から解いてみてください!
図形の面積を周りの長さを求める問題の復習
複雑な図形の面積と周りの長さを求めるには?

補助線を引いて全体を部分と部分に分けよう
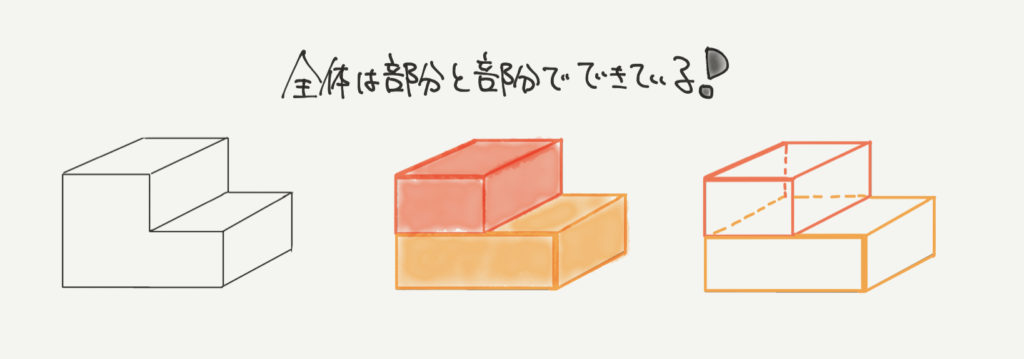
「さんすうがく」の重要なポイントの1つに「全体は部分と部分でできている」という考え方がありました。
特にむずかしい図形や形のときは「全体は部分と部分でできている」考え方を使って、
自分の知っている形に変形させていきましょう。
たとえば上の立体図形では、赤い直方体と黄色の直方体に立体を切り分けることができます!
これが部分と部分に分ける考え方です!
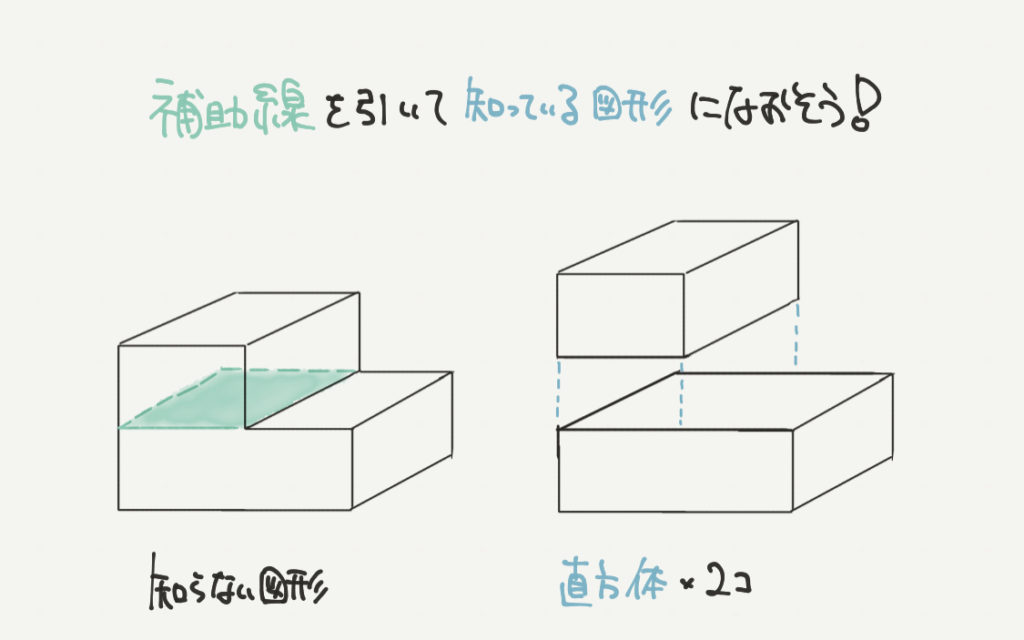
そして全体を部分と部分に分けるとき、大事になってくるのが補助線の考え方でした。
補助線を引くときのポイントはさっきと同じ、自分の知っている形にするために線を引いていきます。
今回の問題ではこの補助線と「全体は部分と部分でできている」という考え方を使いますので、
ぜひ覚えておいてください。
問題に挑戦!
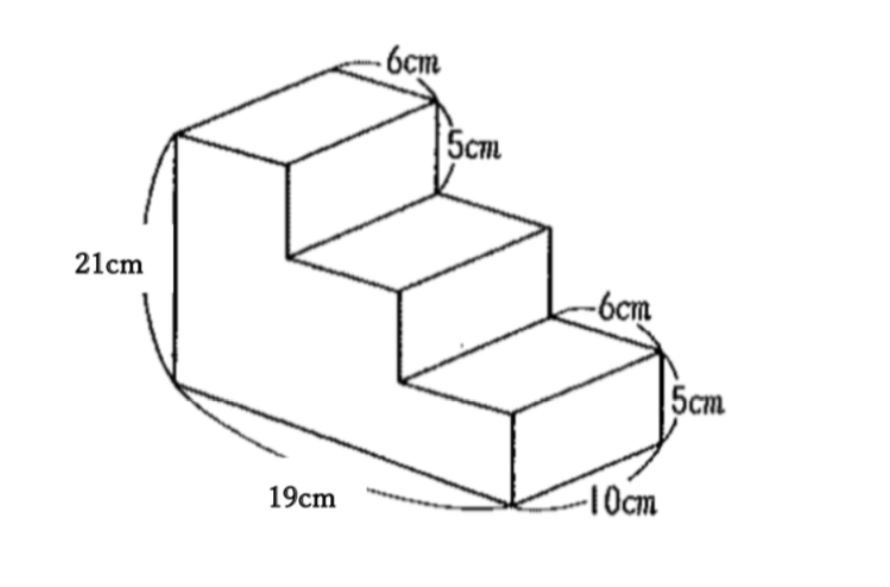
解答
答えを見るにはここをクリック!
①2680㎤
②1456㎠
この記事を書いている人はこんな人


解説を見てみよう!
STEP1:補助線を引いて立体を分けて考えよう
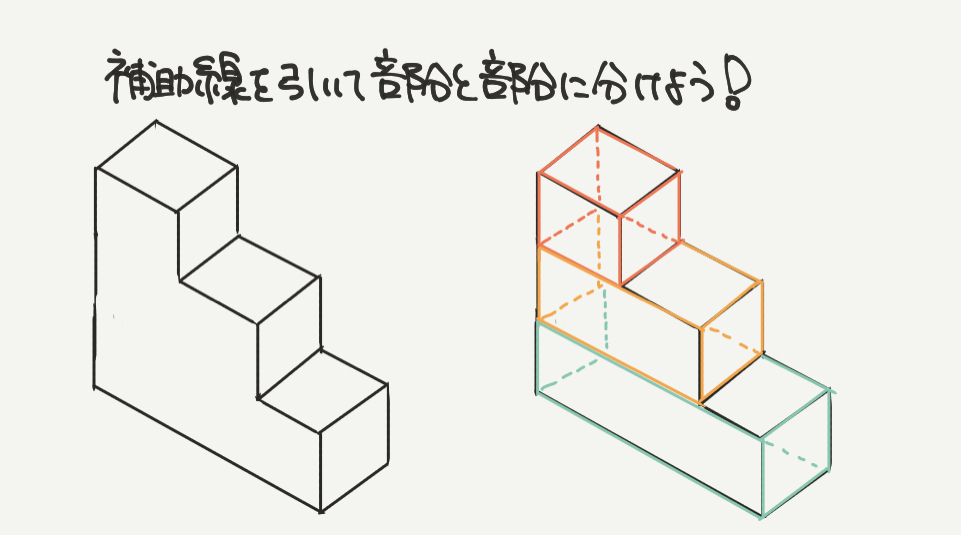
まずはこの複雑な図形に補助線を引いていきましょう。
今回は赤と黄と緑の直方体ができるように線を引いていきます。
すると、右図のように3つの直方体に分けることができました。
これが「全体を部分と部分に分ける」考え方です。
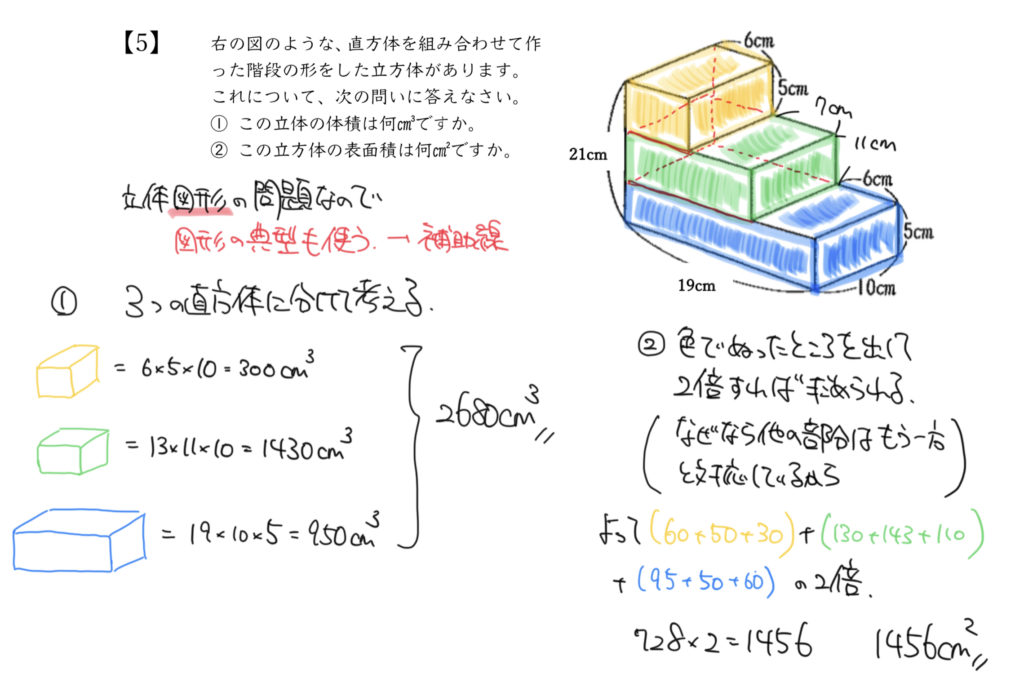
STEP2:赤と黄と緑の体積を求めよう
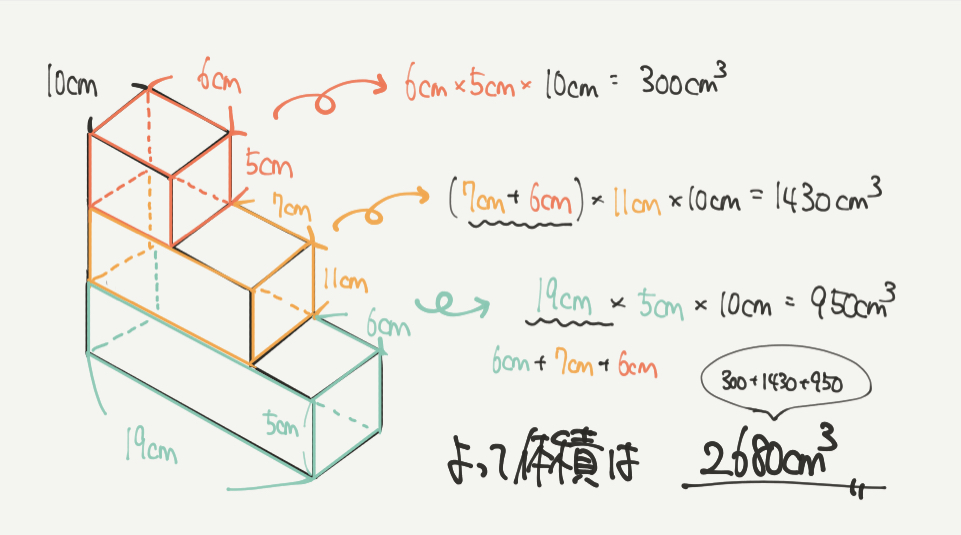
まず求めたいのは体積なので、赤と黄と緑の直方体の体積を計算していきましょう。
ちなみに問題を解くときに必要になってくる7cmと11cmの情報は
問題文から引き算をして求めていきます。
7cm:19cm–6cm–6cm
11cm:21cm-5cm–5cm
そしてここからそれぞれの体積を計算すると・・・!
赤:6cm×5cm×10cm=300㎤
黄:(7cm+6cm)×7cm×10cm=1430㎤
緑:(6cm+7cm+6cm)×5cm×10cm=950㎤
よってこの立体の体積は、
300㎤+1430㎤+950㎤=2680㎤
と計算できました!!
STEP3:表面積は3方向から考える!まずは2方向から
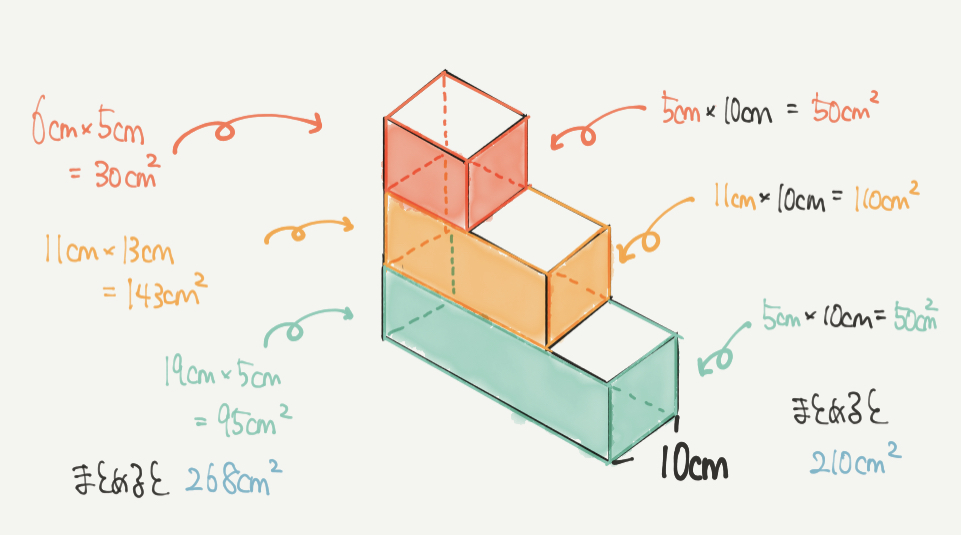
続いて、表面積についてみていきましょう。
ここでポイントですが、表面積を求めるときは全部の面積を求めるよりも
片方の側面の面積を2倍する方が簡単に解くことができます。
どういうことか説明します!
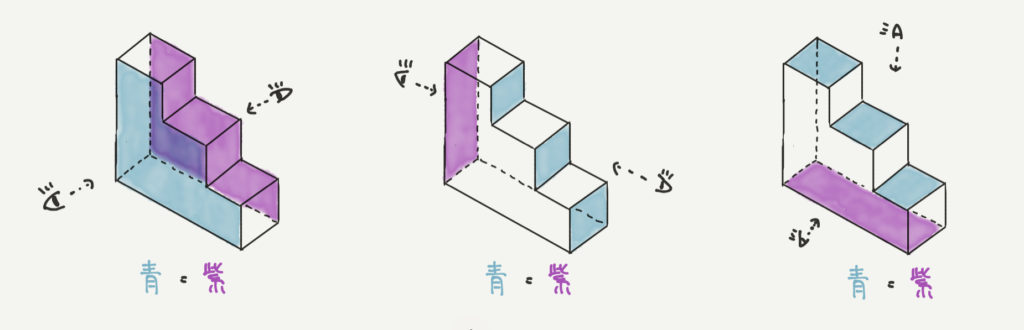
こんな感じでイメージしてみてください。
複雑な立体図形でも同じ部分を見つけることができます。
それぞれ青の面積と紫の面積が等しくなります。
ですので、3方向から見た片方の側面の面積を2倍すれば
表面積を求めることができるというわけです!
STEP4:最後に1方向考えて答えを出そう!
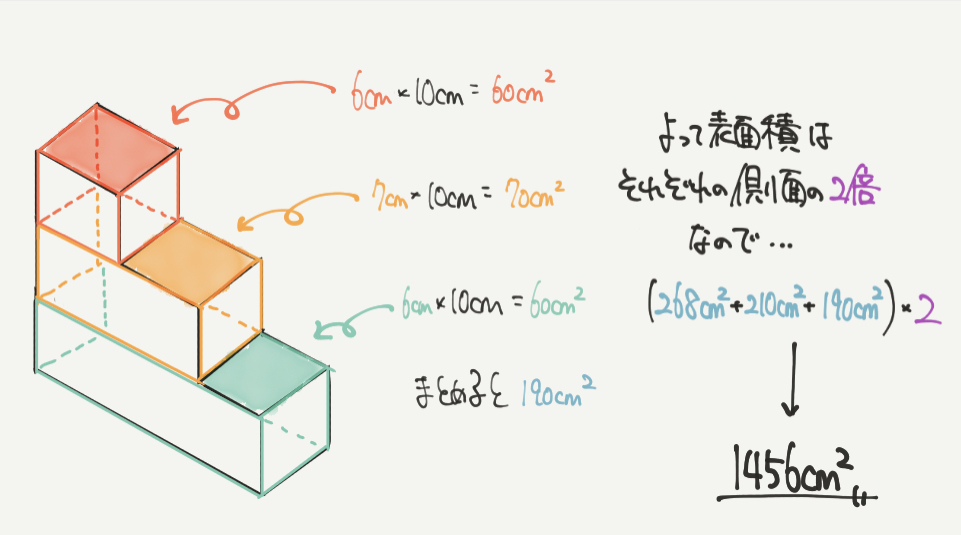
計算式がたくさん多く、イラストきちんと説明しているので文章では書きません。
ですが3方向から見たときの側面積がそれぞれ、268㎠、210㎠、190㎠なので表面積は
(268㎠+210㎠+190㎠)×2倍=1456㎠が正解になります。
複雑な立体の表面積と面積を求める問題のまとめ
今回の問題で大事なポイント
- 補助線の考え方(はじめに、STEP1)
- 「全体は部分と部分でできている」考え方(はじめに、STEP1)
- 立体図形の表面積の求め方(STEP3、4)
・3方向から側面の面積の2倍になる
※どんな立体でもこうなるわけではないので注意してください!
「平面図形」の応用バージョンの複雑な「立体図形」の問題でした!!
体積と表面積、どちらも求めることができましたか?
この問題は今までの復習問題といってもいいでしょう。
もし間違えてしまっていたら原因を突き止めて、改善していきましょう。
解説にも書いてある通り、立体図形の問題にも平面図形の知識を使います。
見慣れない図形(複雑な図形)を補助線を用いて解きやすくするというテクニックを使いましたね!
今回は横に線を引いていますが、もちろんたてに線を引いても解けるので好きなやり方で大丈夫です。
そしてもう一つが「全体は部分と部分でできている」考え方です。
これは中学受験の先生が教えてくれました。
一見むずかしそうな図形や問題文も、実はたくさんの部分でできている。
なので部分と部分に分けて考えれば解きやすくなる、と教わりました。
このむずかしそうに見える立体も補助線を引けばただの直方体の集まりです。
むずかしく考えずに解いていきましょう!