【中学受験攻略】円柱を三等分した図形の体積と表面積の計算方法

はじめに

みなさんこんにちは！
今日勉強する内容は円柱の体積と表面積についてです。
少し変わった円柱の体積と表面積を求めるにはどうしたらいいのか？
さっそく説明していきたいと思います！

円の面積の1/3倍と円柱の体積の1/3倍

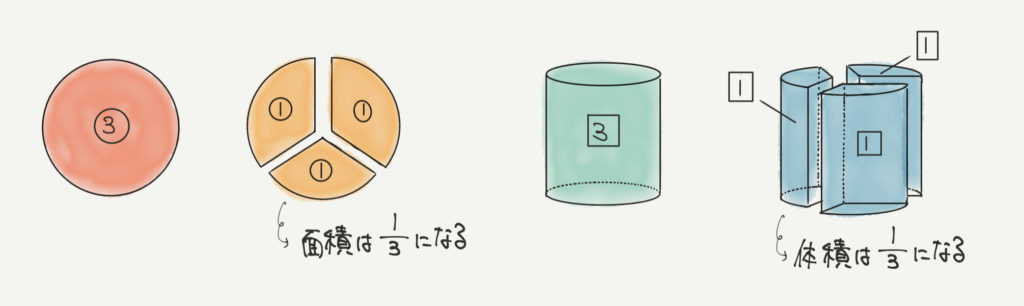
まずは今回の問題を解く上で大切なポイントについて確認しておきましょう！！
赤の図は円の全体を表しています。
そして円の中心から120度の角度で三等分したときの図形が黄色です。
このとき赤円の面積と黄色円の面積の比は3:1になります。
ここまでは「平面図形」の復習でもあるので大丈夫だいじょうぶかと思います。

ポイントはここからです。
次に緑の円柱に注目してみましょう。
そしてこの円柱を120度の角度で三等分したときの立体が青の図形です。
この図形の体積も先ほどと同じ考え方で円柱の1/3の大きさになります。

体積になっても考え方は面積のときと同じであることを覚えておいてくださいね！！
それでは今日の問題に挑戦ちょうせんしていきましょう。

問題に挑戦ちょうせん！

下の図は、円柱の1/3の立体を表しています。
円周率を3.14として、次の問いに答えなさい。

① この立体の体積は何㎤ですか。
② この立体の表面積は何㎠ですか。

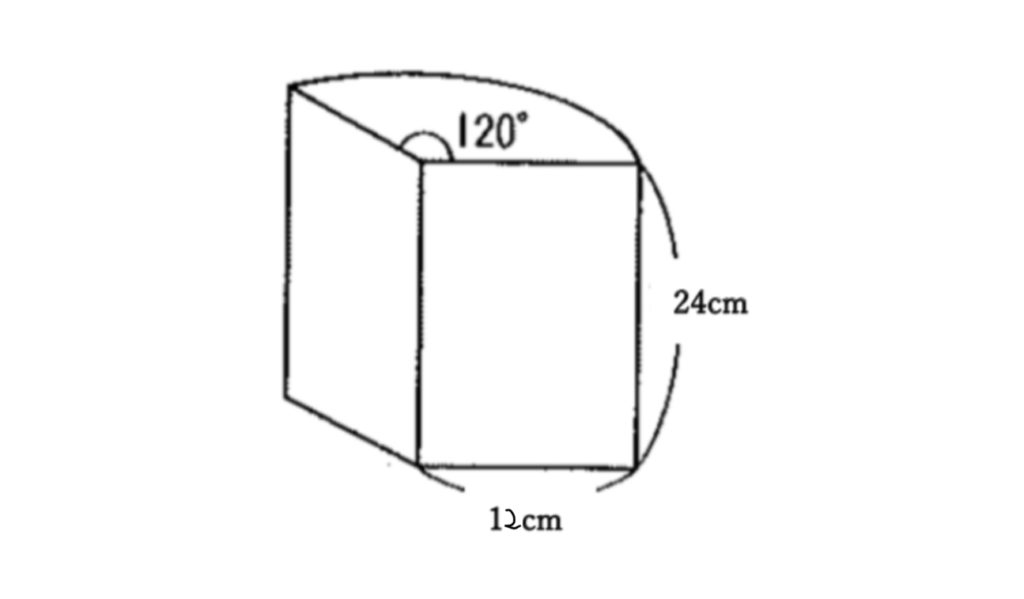
解答

この記事を書いている人はこんな人

解説を見てみよう！

STEP1：体積は円柱の1/3！

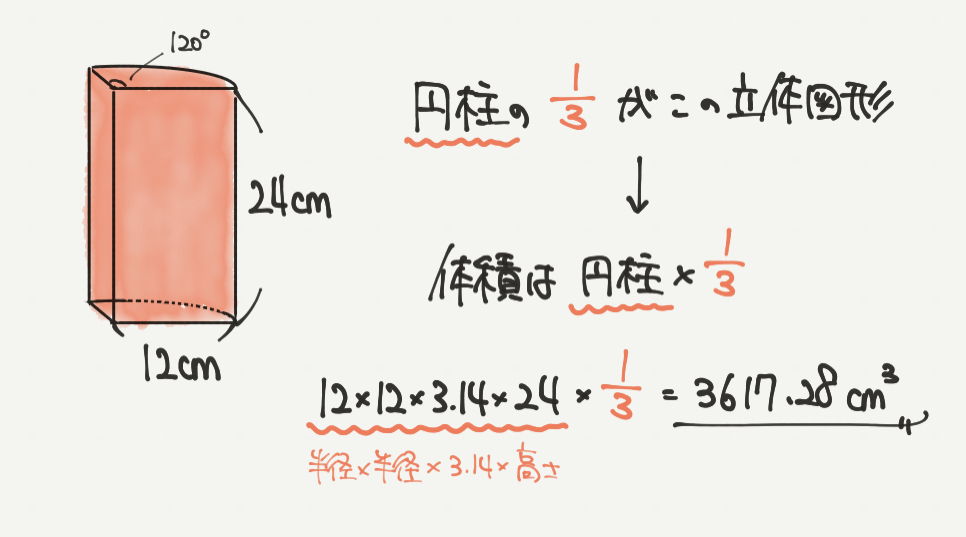
まずは体積を求めていきましょう！

こちらは角度が120度と360度の1/3なので、円柱が1/3になってしまった立体図形です。
体積を求めるために必要なのはこの120度の情報だけです。

なので体積を求めるときは円柱の1/3を求めればいいだけです。
ここでも楽に計算することを意識してみましょう。

求めたい体積：円柱×1/3
=半径×半径×3.14×高さ×1/3
=12×12×3.14×24×1/3
=(12×12×24×1/3)×3.14
=1152×3.14
=3617.28㎤となります。

STEP2：表面積は黄+緑+青で求められる

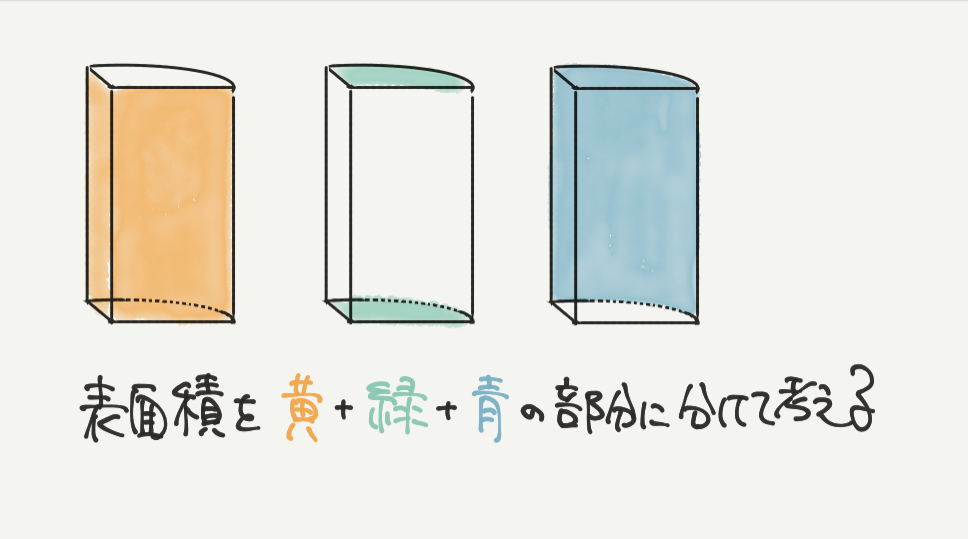
一方で②の表面積を求める問題は少しめんどくさいです。

「さんすうがく」で大切な「全体は部分と部分でできている」考え方を使って、
求めたい表面積を黄+緑+青に分けていきましょう。

すると、この3つに形を分けることができます。
黄：長方形が2つ
緑：おうぎ形が2つ
青：長方形が1つ（展開図を書いてみよう！）

これらの面積を求めていきましょう！！

STEP3：黄と緑の表面積を求めよう

まずは一番かんたんな黄色の長方形から求めていきます。
黄色の長方形1つ：12cm×24cm
黄色の長方形2つ：12cm×24cm×2コ=576㎠となります。

続いて緑のおうぎ形を見ていきましょう。
緑の部分の面積は、1/3の大きさの円の面積２コ分です。

緑のおうぎ形1つ：12cm×12cm×3.14×1/3
緑のおうぎ形2つ：12cm×12cm×3.14×1/3×2コ
=96×3.14になります。
↑120°/360°=1/3

STEP4：青の表面積を求めて答えを出そう

最後に青ですが、問題はこの長方形の横の長さです。
立体図形をよく見てもらうとわかると思いますが、
青の長方形の横の長さはおうぎ形の弧この長さと同じになります。

ですので青の長方形の面積は、おうぎ形の弧この長さ×24cmとなり
おうぎ形の弧この長さ：12cm×2×3.14×1/3
青の長方形の面積：12cm×2×3.14×1/3×24cm=192×3.14

よって答えの表面積は、黄+緑+青なので
576+96×3.14+192×3.14
=576+(192+96) ×3.14
=576+288×3.14
=1480.32㎠

これらを合わせて答えを出しましょう！！

円柱を三等分した図形の体積と表面積を求める問題のまとめ

今回の問題で大事なポイント

• 「全体は部分と部分でできている」考え方（STEP2）
• ×3.14の計算のまとめ方
  ・3.14を最後にしてまとめて考えよう！！

以上が円柱の応用問題の「立体図形」の問題でした！！
体積と表面積、どちらも正解できましたか？

今回も立体図形の少しむずかしい問題でしたね。

これは「立体図形の問題あるある」だと思いますが、
体積を求める問題よりも表面積を求める問題の方がめんどうくさいです。

表面積を求めるときはSTEP2の「全体は部分と部分でできている」考え方を使って、
必ず数え忘れをしないように注意しましょう！！

3.14の計算を楽にする考え方

円の中の斜線部分の周りの長さと面積を求めるには？