【中学受験攻略】立体図形のポイント解説！対角線から立方体の体積・表面積を簡単に求める方法

はじめに

みなさんこんにちは！
最近ずっとお腹がへってしまいます。なんででしょう？笑
さて、そんなことはさておき、今日は立体図形の問題を全4問解いていきましょう。

いつものように立体図形の絵がないので、受験生のみなさんで書いてもらう必要があります。
今までに教えた知識を使って解いていきましょう〜。

展開図を頭の中で組み立ててみよう

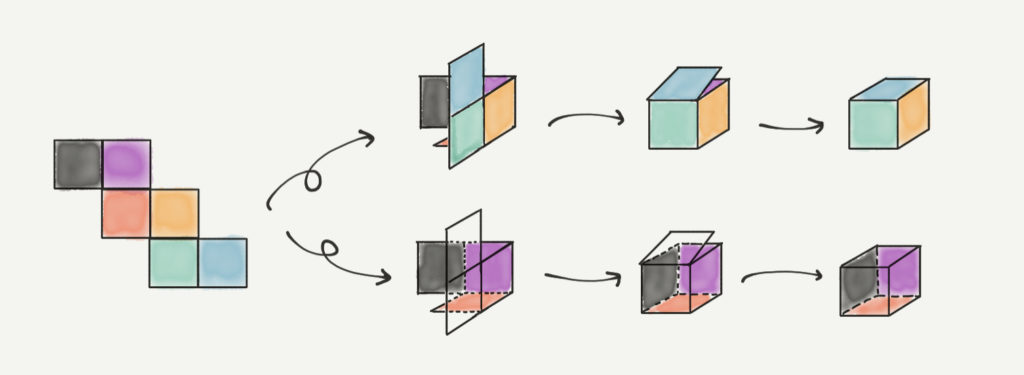
まずは立体図形の基本である、展開図についておさらいしておきましょう。
言葉で説明するのがとてもむずかしいので上の図をよーくみてイメージしてみてください！

展開図を頭の中で組み立てるとき、頭の中ではこのようなことが起きています。
今回は赤い面を下にしています。そのほかの色の面がどのように組み立てられていくのか
想像してみてください。

もしこれがわからなかったら、実際に紙に色をぬって組み立ててみてください。
一度イメージを見ておくとグッとわかるようになりますよ！

正方形の面積の求め方

続いて正方形の面積に関する知識です。
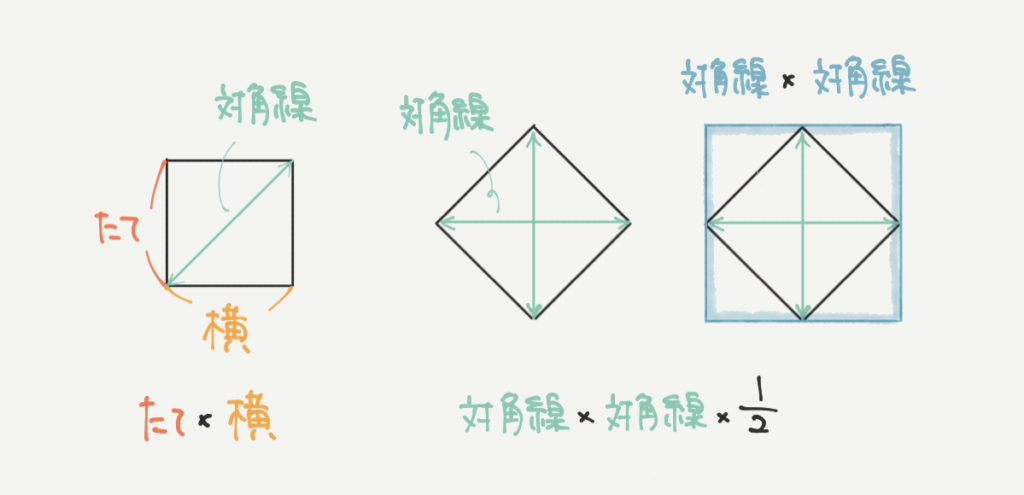
正方形の面積は2つのやり方で求められることを知っていますでしょうか。

1つ目は「たて×横」で求められますね。

そしてポイントとなるのがもう1つの「対角線×対角線×1/2」です。
正方形の面積は対角線の長さからだけでも解くことができます。

対角線×対角線=青の大きな正方形
大きな正方形の半分が求めたい面積。
だから対角線×対角線×1/2なんだね！！

今回の問題ではこれを使いますので、ぜひ覚えておくようにしましょう。

問題に挑戦ちょうせん！

次の問いに答えなさい。

① 1つの対角線の長さが8cmの立方体の表面積は何㎠ですか。
② 表面積が216㎠の立方体の体積は何㎤ですか。
③ 底面が1辺10cmの立方体の容器に水を540㎤入れると、水の深さは何cmになりますか。
④ たて8cm、横10cmで、表面積が592㎠の直方体の高さは何cmですか。

解答

この記事を書いている人はこんな人

解説を見てみよう！

STEP1：1つの対角線から立体の表面積を求めよう

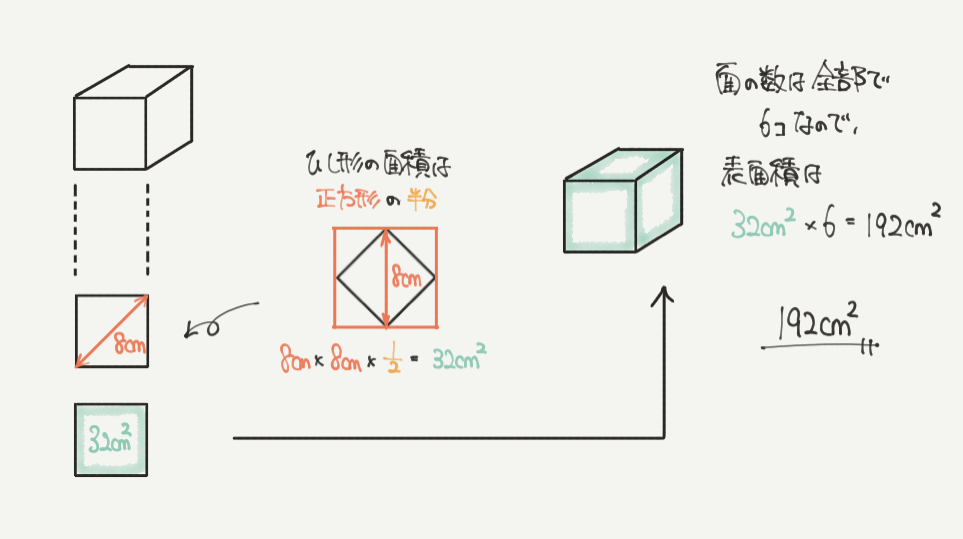
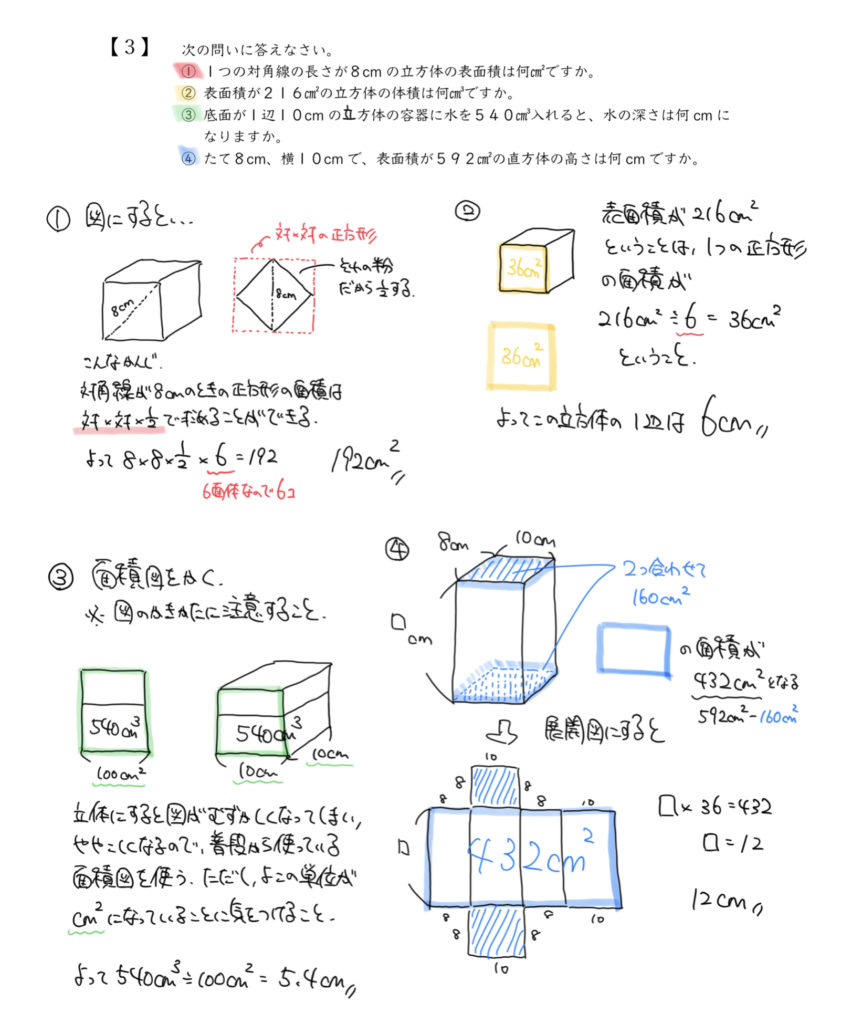
まずは①の問題から解いていきましょう。

こちらの立体は立方体と言われているので、こちらの図形は全て正方形であることがわかります。
そして正方形の対角線が8cmと言われているので、1つの正方形の面積を求めていくと・・・

ひし形（今回は正方形）の面積は、
対角線×対角線×1/2
=8cm×8cm×1/2
=32㎠となります。

今回知りたいのは表面積なので、６面ある立方体の表面積は
32㎠×6=192㎠になります。

STEP2：表面積から立方体の体積を求めよう

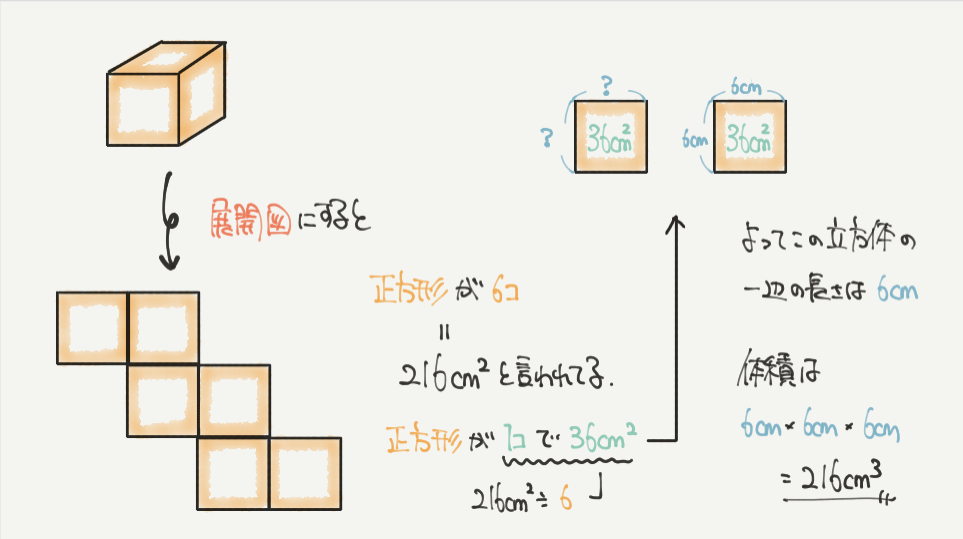
続いて②の問題です。
こちらの問題もそこまでむずかしくはありませんので安心してください。

②では6つの面全ての表面積が216㎠と言われていますので、
正方形×6コ=216㎠
正方形×1コ=36㎠

よって正方形の1つの辺の長さは6cmとなります。
ここから立方体の体積を6cm×6cm×6cm=216㎤と計算することができました。

STEP3：立方体の容器に入っている水の深さを求めよう

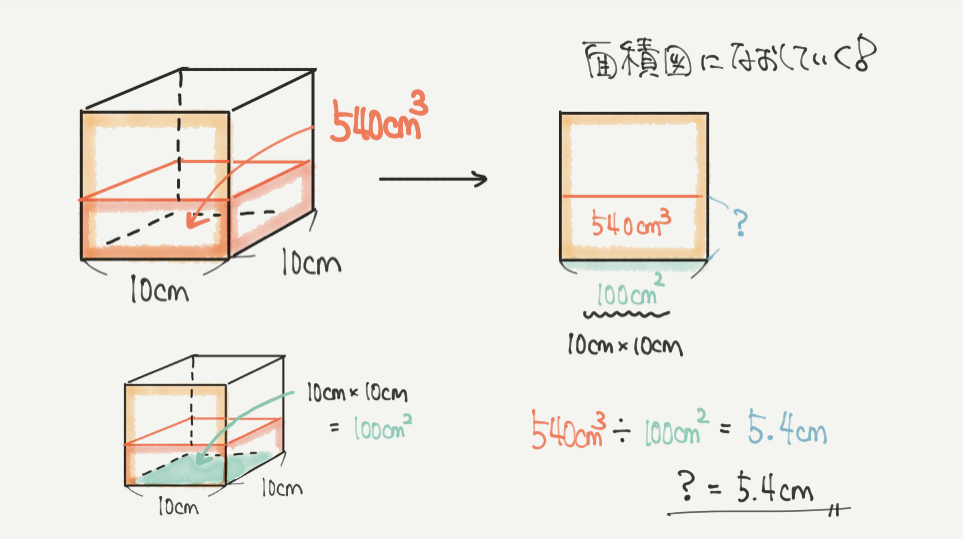
③の問題では見取り図の図形でまずはイメージをして、面積図に変えながら問題を解いていきましょう。

一辺が10cmの立方体に540㎤の水を入れていきますので、これを面積図に直すとどうなるでしょうか？
ここで注意です！！！

面積図は立体図ではないので、底辺の長さが面積に直すと変わっていることに気をつけます。
面積図の底辺は10cm×10cmなので100㎠を書きかえて計算します。

よって水の深さは面積図より、
540㎤÷100㎠=5.4cmになりました。

STEP4：直方体の長さを求めよう

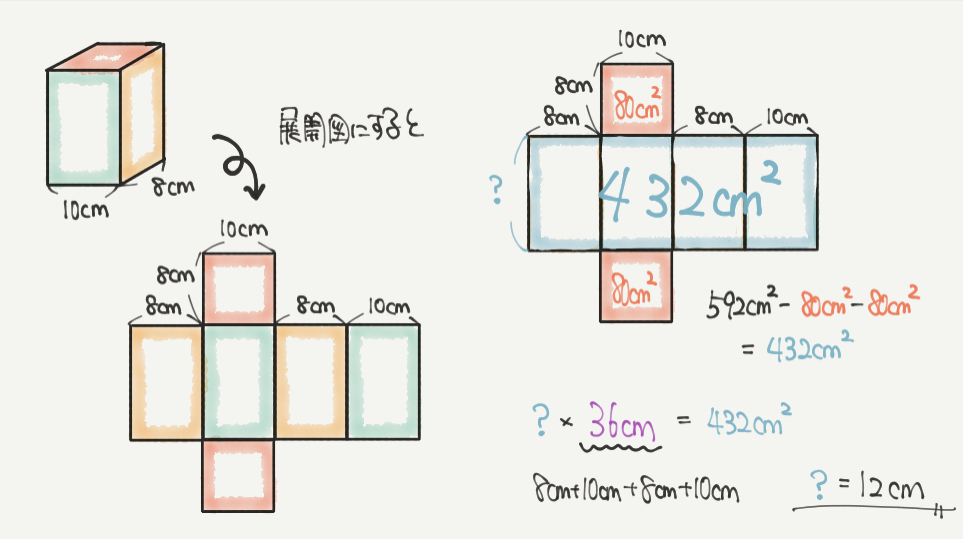
④の問題は展開図の問題でした。この問題は展開図にすると一発で求めることができます。

見取り図から展開図に書き直せるかが最初のポイントです。
展開図を書いたら、問題文に書いてある長さもわかるところから埋めていきましょう。
この時点でわかっているのは赤い四角形の表面積が160㎠（80㎠×2）です。

よって592㎠から160㎠を引いた432㎠が残りの面積になりますので、書いた展開図と合わせて考えると、

？（たて）×（8cm＋10cm＋8cm＋10cm）=432㎠
？（たて）×36cm=432㎠
？（たて）=12cm

12cmと答えを求めることができます。

対角線から立方体の体積と表面積を求める問題のまとめ

今回の問題で大事なポイント

• 見取り図から展開図への頭の中の考え方（はじめに、STEP4）
  ・文章での説明はとてもむずかしいので紙を使って実際にやってみましょう！
  
• 正方形の面積の求め方（はじめに、STEP1）
  ・対角線×対角線×1/2
  ・たて×横

「立体図形」の基本問題がたくさんあった4問だったと思います。
4問中何問正解できましたか？？
これらの文章題の問題は、問題を頭の中で正しくイメージできることが大切です。

ただ頭の中で図形をイメージしたり、計算するのってすごく大変です。
私も絶対に頭の中だけでは計算しません。必ず紙に図を書くようにしています。

どんな問題でもまずはしっかり図を書くこと。
そうすることで見直しのときや、解き直しをするときにどこで間違まちがえたのかがわかるので、
必ず皆さんのレベルアップにつながります。