【中学受験攻略】立体図形の基本！立方体と円柱の体積比をわかりやすく解説

はじめに

みなさんこんにちは！
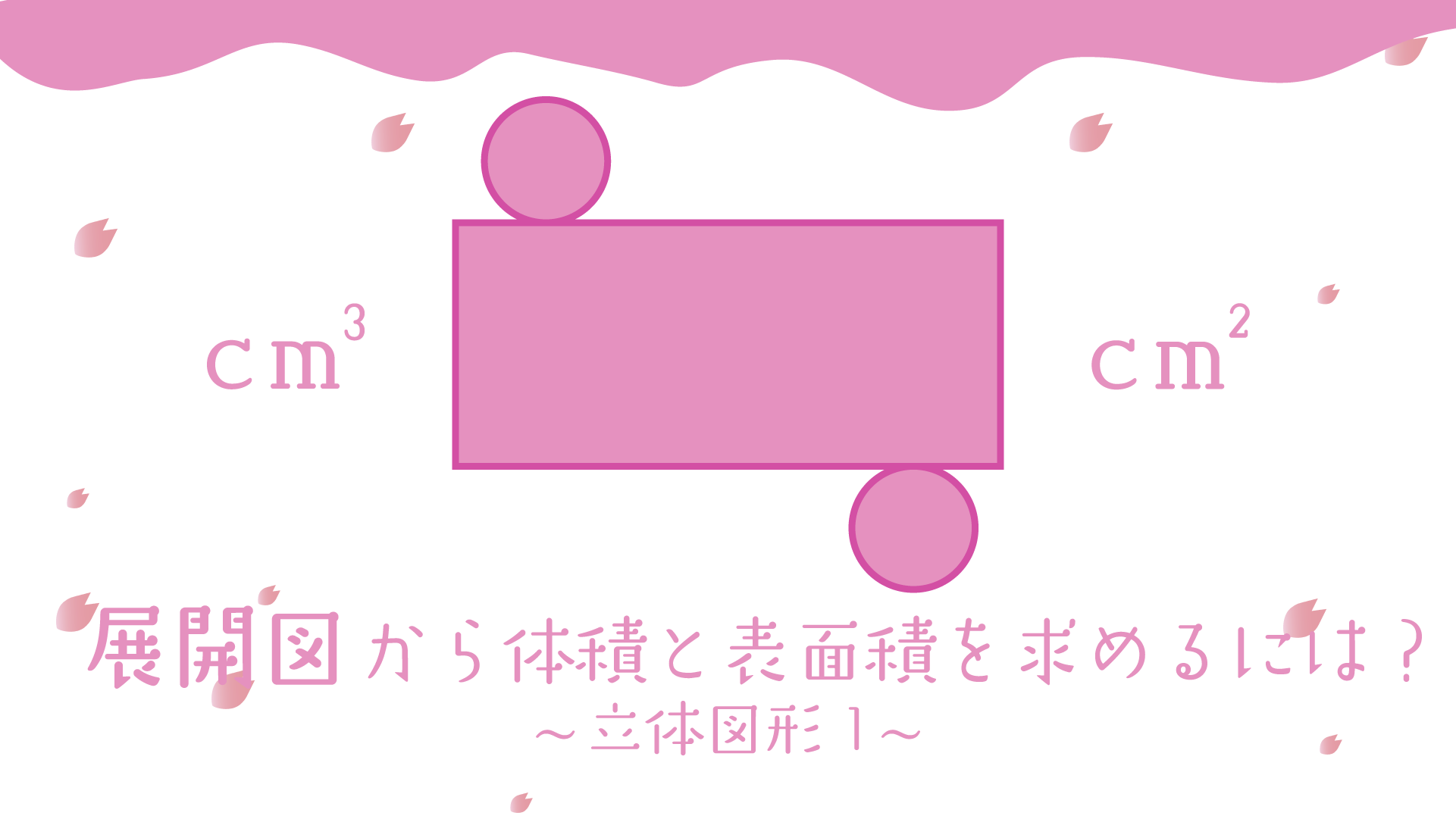
今回の問題は円柱の展開図を使って、立体図形の体積と表面積を求める問題です。
早速ヒントから見ていきましょう～！

円柱の展開図

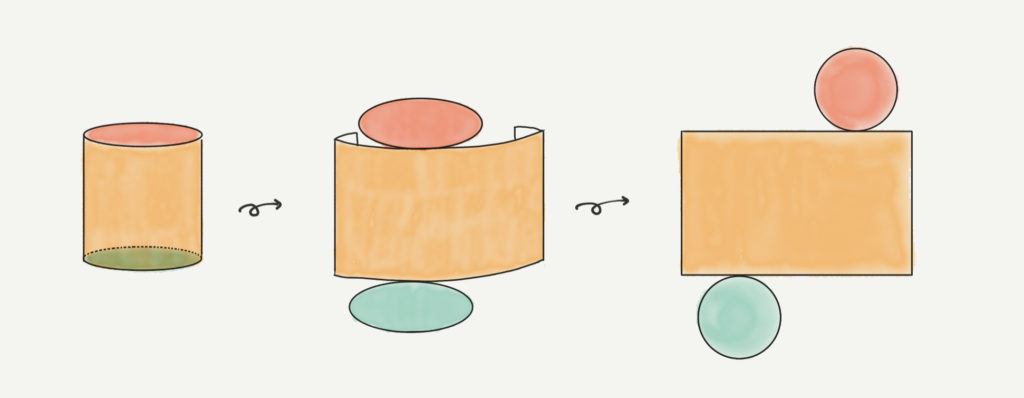
今回の問題では円柱の展開図が出てきます。

円柱の展開図は赤い円と緑の円、そして黄色の長方形でできています。
展開図だけ見るとわかりづらいですが、真ん中の図をみていただけるとイメージしやすいかと思います。

頭の中でチョキチョキ図形を切って、広げるイメージをしておきましょう。
ちなみにもう一つ大事なことがあるんですが、それは問題を解いていく中で説明します！！

今回の問題ではこの円柱の展開図について解いていきましょう。

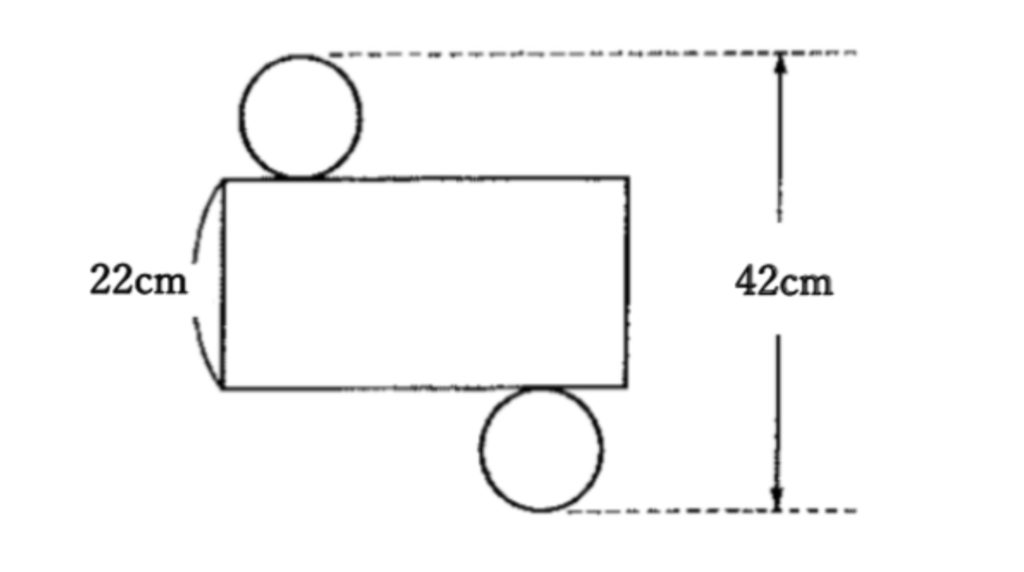
問題に挑戦ちょうせん！

下の図は、ある立体の展開図です。これを組み立ててできる立体について、次の問いに答えなさい。
ただし円周率を3.14とします。

① この立体の体積は何㎤ですか。
② この立体の表面積は何㎠ですか。

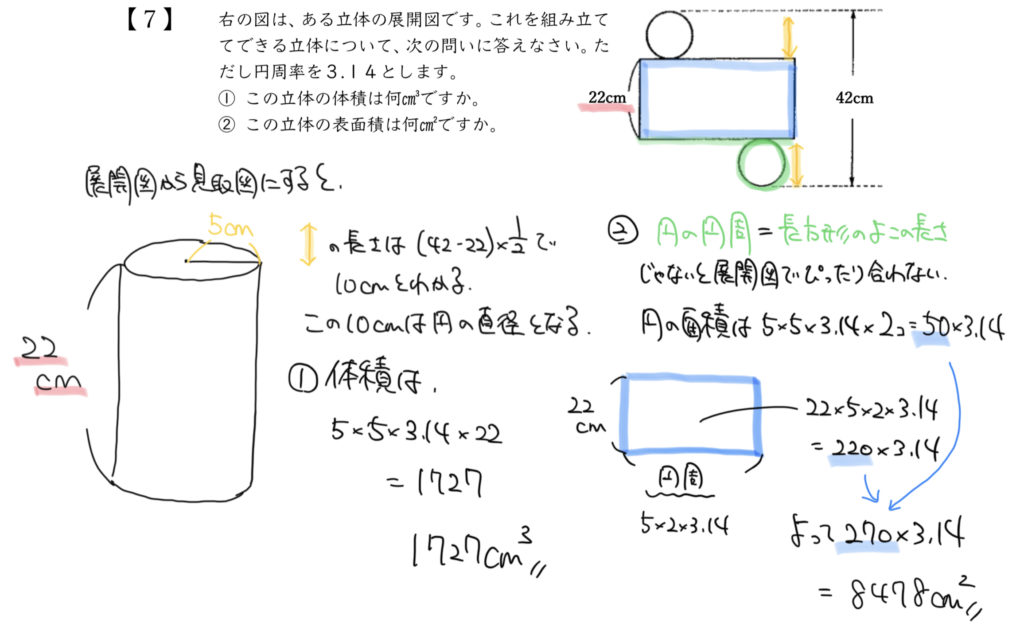
解答

この記事を書いている人はこんな人

解説を見てみよう！

STEP1：展開図に情報を書きこもう

さあ、まずは展開図に問題文からわかることを書いていきましょう。
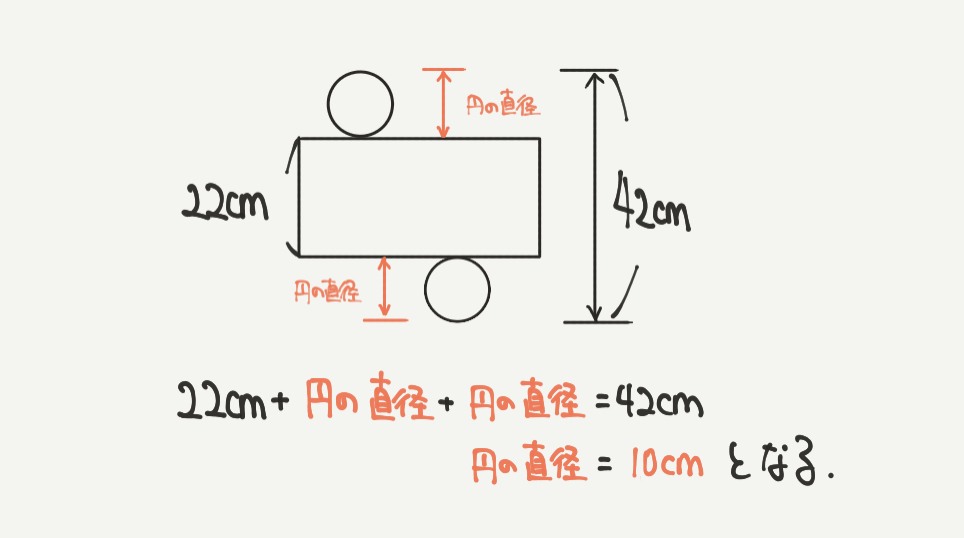
今回問題文で書かれている情報は42cmと22cmです。

そしてポイントになってくるのが円の直径の長さです。
問題文の図を見ると、
42cm=22cm+円の直径+円の直径となります。

ここから、
円の直径+円の直径=20cm
円の直径=10cm
とわかります。

ここまでがSTEP1です！！

STEP2：円柱の体積を求めよう

円の直径=10cmとわかったので、円の半径は半分の5cmになります。
円柱の体積は、「半径×半径×3.14×高さ」で求めることができますので、

①の答え（円柱の体積）は、
5cm×5cm×22cm×3.14になり、×3.14を最後に計算すると・・・

5cm×5cm×22cm×3.14
=550×3.14
=1727㎤になりました。

STEP3：「全体は部分と部分でできている」「同じところを見つける、つくる」

続いてこの展開図の表面積を計算していきます。
ここで使うのがSTEP3：「全体は部分と部分でできている」考え方と
「同じところを見つける、つくる」の考え方です。

「全体は部分と部分でできている」

この展開図は緑の円と青の長方形の部分でできています。
ですのでこの展開図の表面積を求めるには円+円+長方形で考えていきましょう。

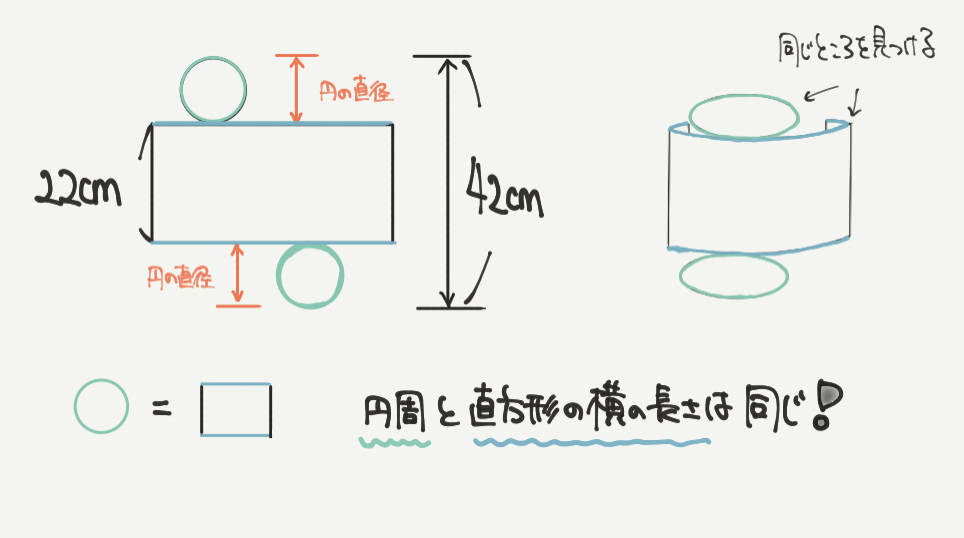
「同じところを見つける、つくる」

そして円柱の展開図で大事なポイントになってくるのが長方形の横の長さです。
右の図を見ていただけるとわかると思いますが、この長方形の横の長さと円の周りの長さが同じになります。
つまり、長方形の横の長さ=円周ということです。

STEP4：展開図の部分の面積を求めよう

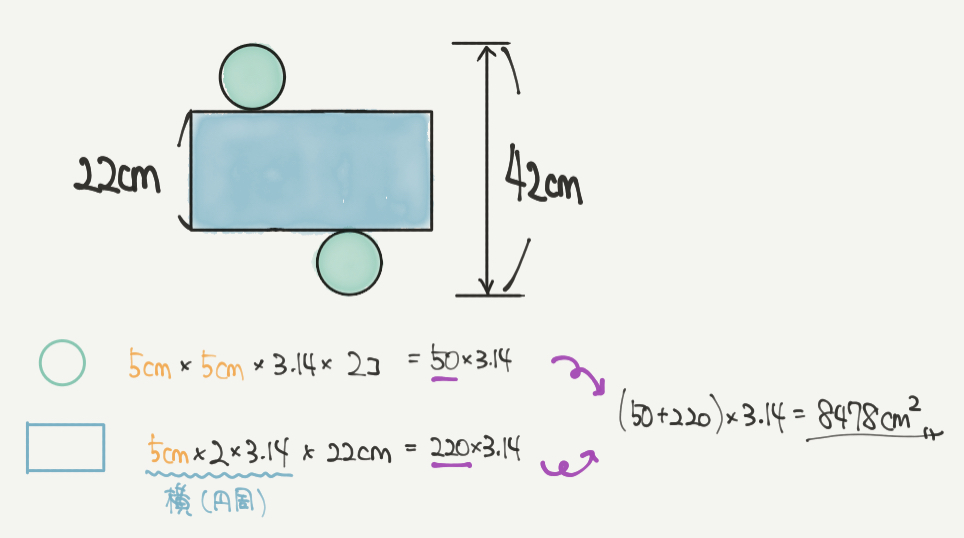
緑の円の面積：5cm×5cm×3.14
緑の円の面積が2個分：5cm×5cm×3.14×2コ

青の長方形：たて×横
青の長方形：22cm×円周
青の長方形：22cm×5cm×2×3.14

よって表面積の合計は、
緑の円の面積が2個分：50×3.14
青の長方形：220×3.14

（50+220）×3.14
=270×3.14
=8478㎠と求めることができました！

50×3.14＋220×3.14＝（50+220）×3.14
↑ここの意味がわからない受験生は下の記事から3.14の計算の考え方を読んでみてください！！

3.14の計算を楽にする考え方

円の中の斜線部分の周りの長さと面積を求めるには？

展開図から円柱の体積と表面積を求める問題のまとめ

今回の問題で大事なポイント

• 立体図形で大切な3つの言葉（復習）
  ・見取り図：いつもよくみる図形、立体的に見える図形のこと
  ・投影図：真上、正面から見たときに見える図形、平面に見える
  ・展開図：立体を切って広げたときにできる図形
  
• 「同じところを見つける、作る」考え方（はじめに、STEP3、4）
  ・円周と長方形の横の長さは同じ
• 「全体は部分と部分でできている」考え方（はじめに、STEP3、4）

展開図の応用問題でした。
いつもみたいな立方体や直方体ではなく、円柱のときの展開図は理解できたでしょうか。
体積と表面積、どちらも求めることができましたか？

この「立体図形」の問題は実際に自分で紙を使って勉強していくのが一番です。
もちろん紙を切ったりするのも時間がかかるので、
お父さんお母さんにお願いして作ってもらうのもいいかもしれません。

両方正解できた受験生も、ちゃんと紙を使ってイメージすることは、
さらに理解を深めるために必ず大切になりますので、
もし時間があるならぜひ紙を使いながら復習してみてください！！