【中学受験攻略】平面図形を回転させて立体図形を作る：体積比/側面積比/表面積比の計算方法

はじめに

みなさんこんにちは！
今回は平面図形を回転させる問題です！
立体図形の問題はまだまだ続きますので、一緒いっしょに解いていきましょう～！

平面図形を回転させるときのイメージ

三角形を回転させてみよう

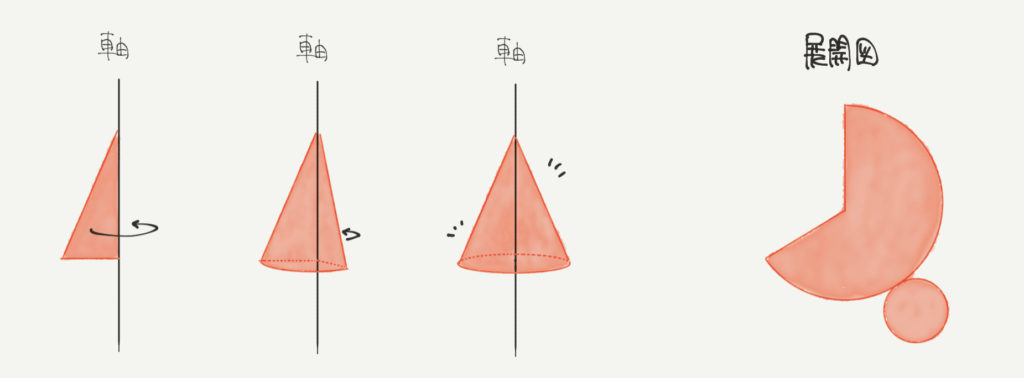
今回の問題では平面図形を回転させるというキーワードが出てきます。
ここで平面図形を回転させて立体図形にするイメージを確認しておきましょう。

回転させるときにポイントになるのが「軸じく」です。
「軸じく」は図形を回転させるときの中心になりますので、この「軸じく」は動きません。

上の図の三角形を見てもらうと、三角形の一辺を「軸じく」に回転させて円すいを作っていますね。

円すいの展開図も復習しておきましょう！円すいの展開図は「おうぎ形と円」でしたね！！

四角形を回転させてみよう

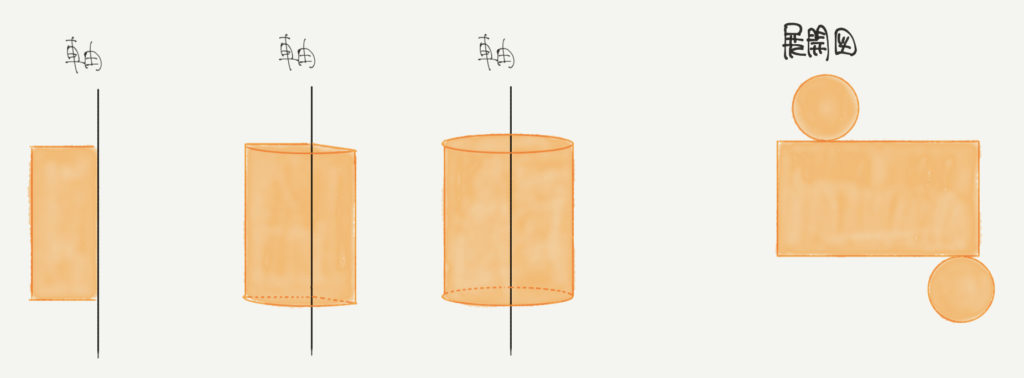
続いて四角形も回転させていきます。
考え方はさっきと同じなので、説明はほとんどありません。

この場合も「軸じく」に気をつけて回転させていきます。
このとき、できる立体図形は円柱なので、円柱の展開図も書いてみましょう！
円柱の展開図は「長方形と円2つ」でできていましたね。

今回の問題ではこの平面図形から立体図形のイメージができていればかんたんに解くことができます。

問題に挑戦ちょうせん！

たて4cm、横8cmの長方形があります。
この長方形を横の辺を軸じくとして一回転させてできる立体について、次の問いに答えなさい。
ただし、円周率は3.14とします。

① この立体の体積は何㎤ですか。
② この立体の表面積は何㎠ですか。

解答

この記事を書いている人はこんな人

解説を見てみよう！

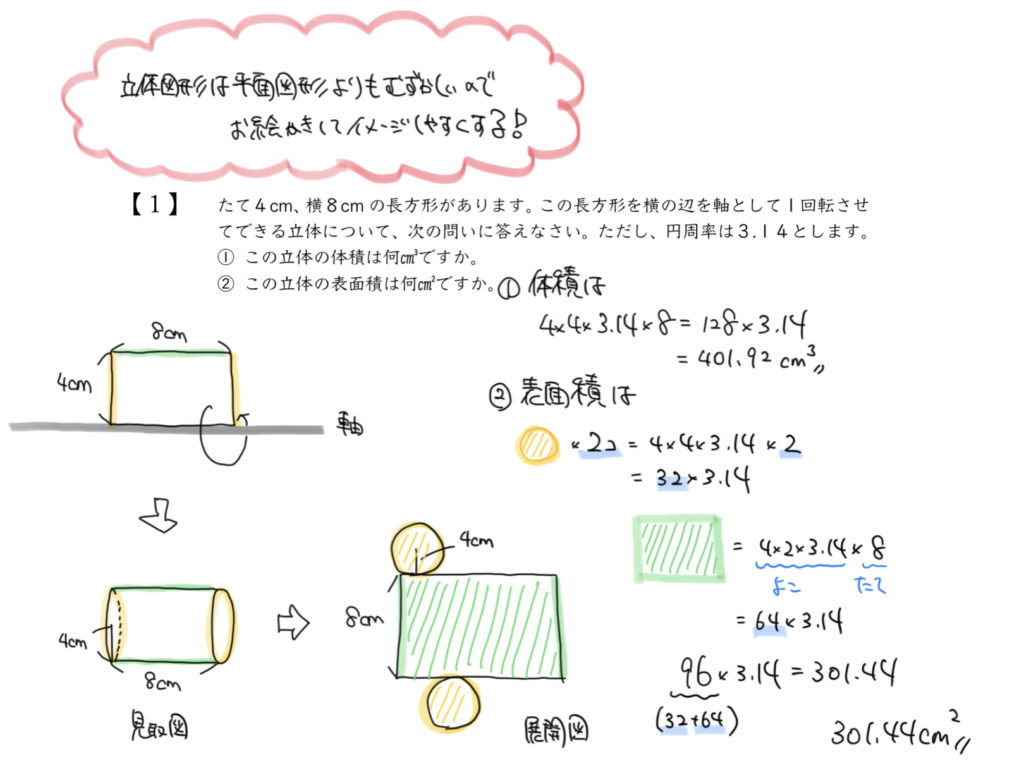
STEP1：平面図形から立体図形をイメージしよう

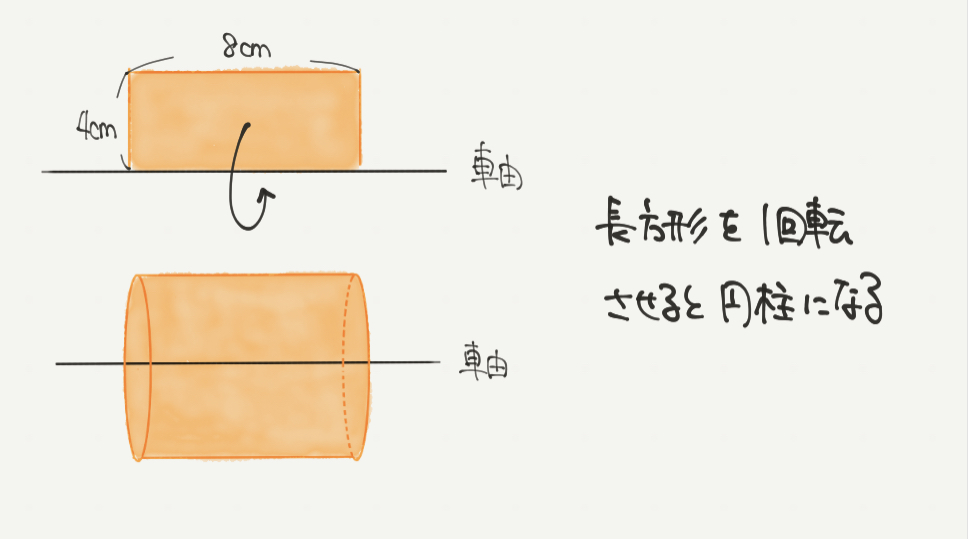
まずは問題文の内容をきちんと図にしていきましょう。
回転させる図形はたて4cm、横8cmなので横に長い長方形ですね。

そして「軸じく」は横の辺なので、横の辺を中心に図形を一回転させていきましょう。

すると円柱ができると思います！！

今回はこの円柱の体積と表面積を求めればOKです。

STEP2：円柱の体積を求めよう

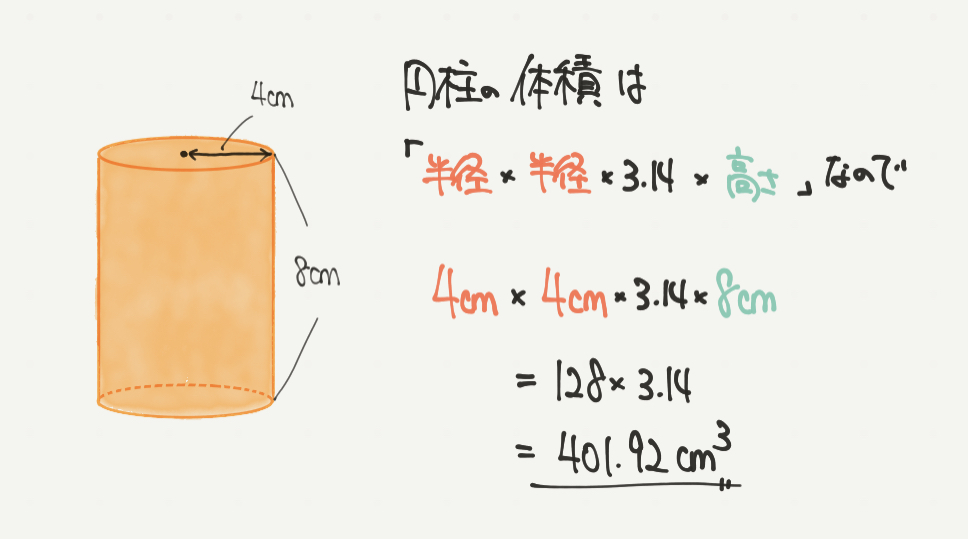
それでは、円柱の体積を求めていきましょう。

計算をわかりやすくするために円柱の向きを変えましたので注意してくださいね。

円柱の体積は「半径×半径×3.14×高さ」なので、今回の図形に数字を当てはめると、

4cm×4cm×3.14×8cm
=128×3.14
=401.92㎤

と計算することができます！！

先に×3.14の計算をしてしまうとめんどくさいので、最後にまとめてやりましょう！

STEP3：円柱の展開図を書いてみよう

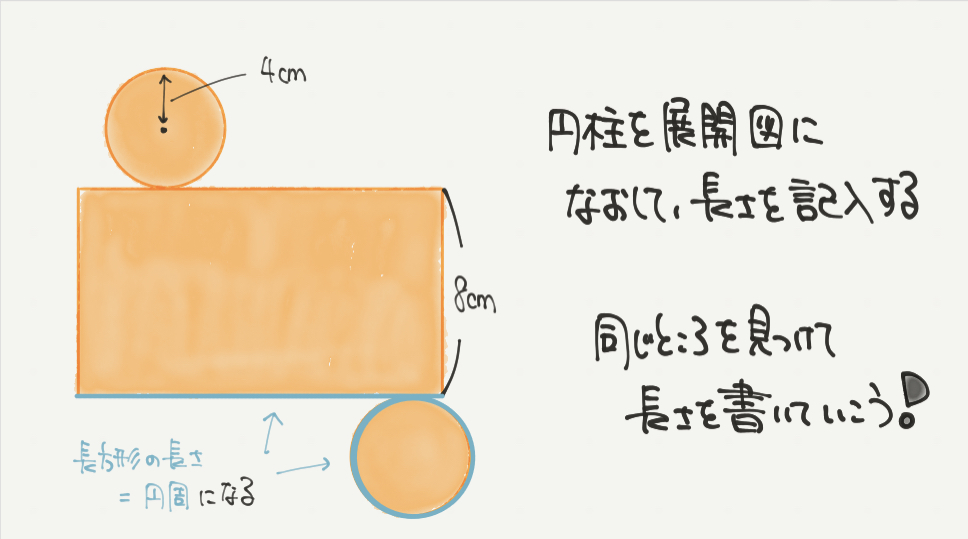
続いては表面積を求めていきましょう。

表面積は見取り図でも求めることができますが、
展開図を書いておくとケアレスミスを無くせますのでぜひ書くようにしましょう。

プチ復習：見取り図と展開図ってなんだったっけ？

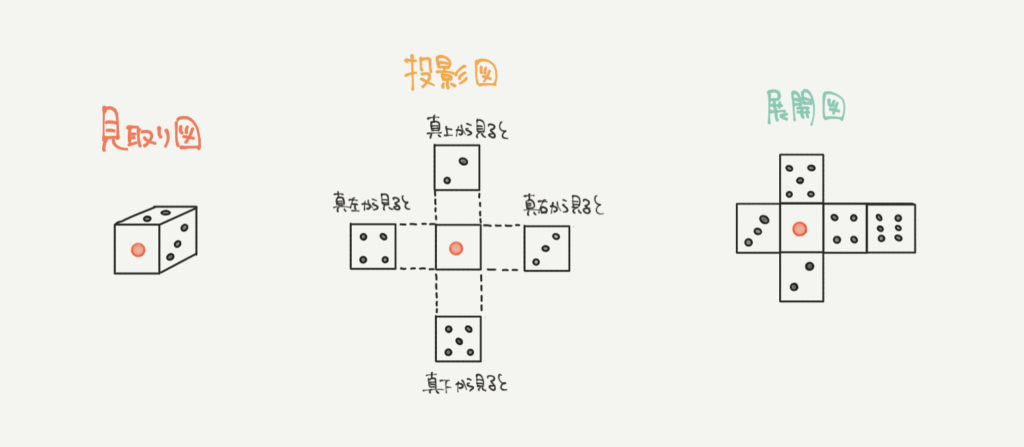
サイコロを例にとって考えてみましょう。

見取り図：いつも見ている図形。よくある図形。
投影図：立体図形を正面や真上から見たときの図。
展開図：立体を切って平面に直したときの図。
でしたね！！

話をもとにもどします。
円柱の展開図は「長方形と円2つ」でした。

そしてこの長方形の横の長さと円周の長さが同じになるのがポイントです。
↑この展開図を組み立てると円柱になるので、ピタッと重なるはず！！

STEP4：楽に計算して表面積を求めよう

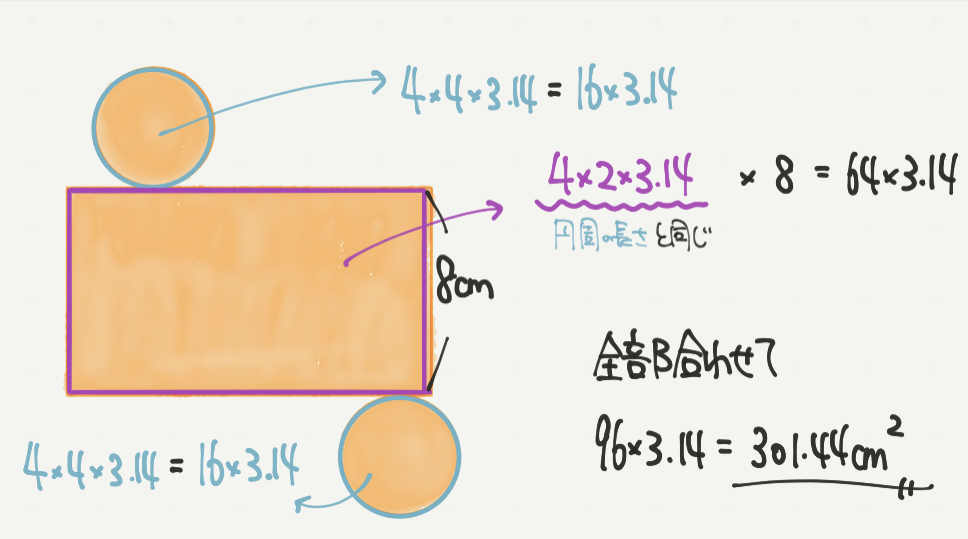
最後は計算あるのみ。
ここで気をつけてもらいたいのが3.14の計算の仕方です。

はじめに×3.14をしてしまうと計算がずっとめんどくさくなるので、×3.14は最後にやりましょう。

円2つの面積：4×4×3.14×2個こ=32×3.14
長方形：4×2×3.14×8=64×3.14

よってこの立体の表面積は、
（32+64）×3.14
=96×3.14
=301.44㎠

と計算できました！！

プチ復習：×3.14をかんたんにやろう

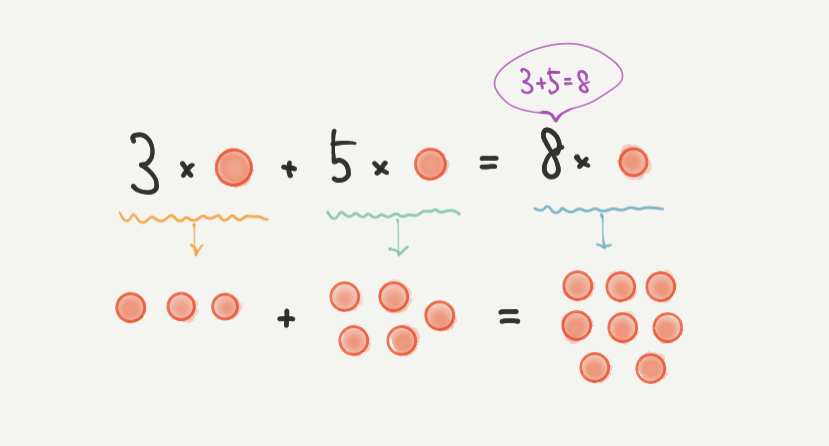
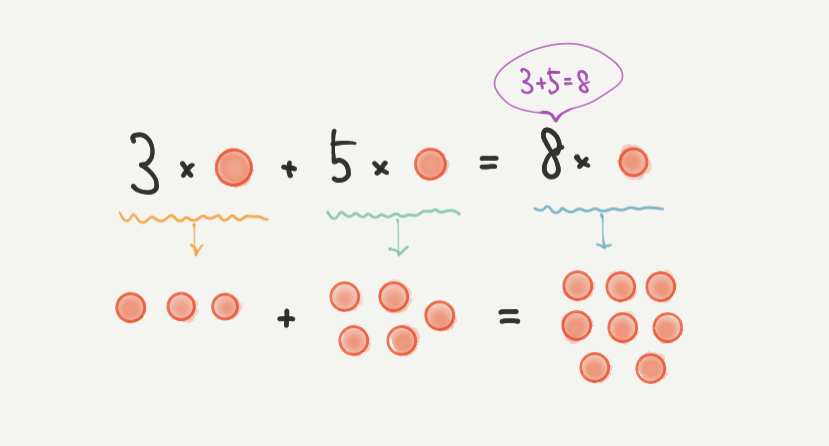
3.14の計算のコツを覚えると、計算スピードがグッと早くなるのでとてもおすすめですよ！

たとえばこちらの図では3×●+5×●という式を表しています。
このときの計算は、（3+5）×●と楽にすることができましたね。

同じように3.14でもまとめて計算することができるのがポイントでした。
32×●+64×●=（32+64）×●になります！

平面図形を一回転させた時の体積と表面積を求める問題のまとめ

今回の問題で大事なポイント

• 平面図形から立体図形に変わるときの考え方
  
• 立体図形で大切な3つの言葉（復習）
  ・見取り図：いつもよくみる図形、立体的に見える図形のこと
  ・投影図：真上、正面から見たときに見える図形、平面に見える
  ・展開図：立体を切って広げたときにできる図形
  
• 「同じところを見つける作る」考え方
  ・展開図を書くときは同じ部分に注目しよう
  
• 3.14の計算のまとめ方

こちらで平面図形を一回転させた時の体積と表面積を求める問題はおしまいです。
みなさんはきちんと立体図形とその展開図を書くことができましたか？？

今回の記事でポイントとして書きましたが、
算数の問題はまずはイメージすることが何よりも大事です。

問題のおおまかな内容を理解しないと何を求めたらいいのか何かわからないからです。
立体図形の苦手な受験生はそもそもイメージができていないことが多いです。

例えば立方体を切ったりするとき、なんとなく感覚で線を引いたりはしていませんか？
表面積を求める問題で、展開図にせずにそのまま気合いで計算してしまっていませんか？

立体図形の単元だけでなく、算数の問題ではまず図を書くことが大切です。
図にするのが難しいのならまずは絵にしてみましょう。

面積図や線分図ではなく絵の方がかきやすくないですか？最初はそれでも全然構いません。
まずはイメージして、そこから図に落とし込んでいきましょう。

この問題の場合、お絵かきは最初の四角形と軸じくです。
これを一回転させたらと想像して書いたのが下の見取り図になります。
そこから展開図を書き、解いていきます。

このようにむずかしい問題でも絵にすること、図にすることを心がけていくと
わからなかった部分が少しずつ解けるようになると思いますよ！