【中学受験攻略】展開図を使って直方体のひもの長さを簡単計算！

2024年1月8日

はじめに

みなさんこんにちは！
今日のテーマも「平面図形」から少しレベルアップした、
中学受験算数の「立体図形」について説明しています。

「立体図形」について今日も問題を解いていきますが、大切な3つの言葉を覚えていますか？
「見取り図」「投影図」「展開図」の3つでしたね！

これらの言葉が今回の解説にも出てきますので、まずはこの言葉から復習しましょう！

「見取り図」「投影図」「展開図」の復習

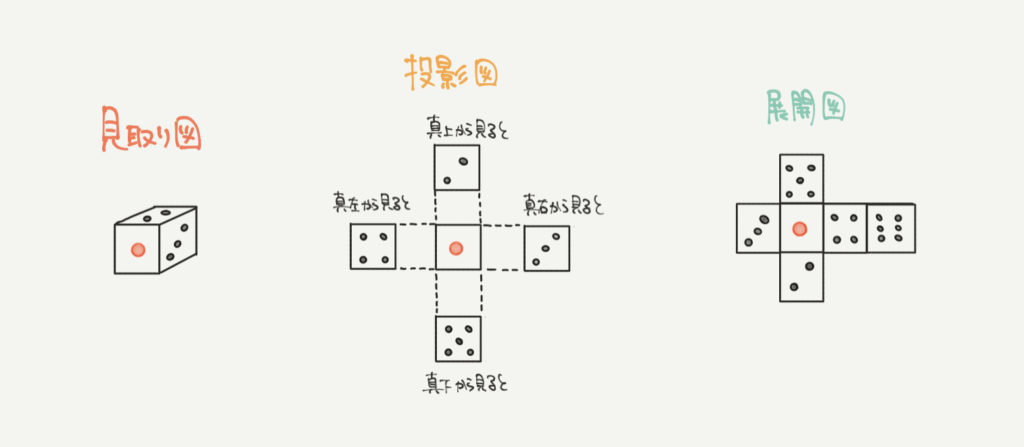
見取り図：いつもよくみる図形のことです。この図で言うと一番左のサイコロの絵が見取り図になります。

投影図とうえいず：図形を真上や真横から見たときの図形です。立体図形の応用問題とかによく出たりします。この絵だと真ん中の図になります。上から見たり左から見たりするとどう見えるのか？についての図です。

展開図てんかいず：展開図は立体を切って広げたときでできる図形のことです。紙パックの牛乳とかを広げたりすると展開図になります！サイコロもハサミでチョキチョキ切ると一番右の図のような展開図になることが想像できると思います。

見取り図から展開図を書いてみよう

こちらでは見取り図から展開図について説明していきます。
頭の中で、どうやって考えれば展開図が書けるのか？しっかり説明していますのでよく読んでくださいね！

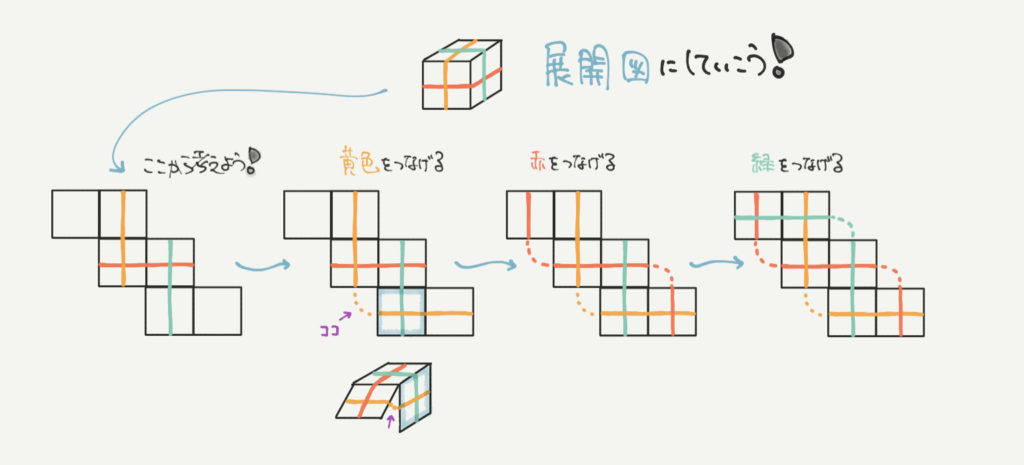
まずは見取り図から見える部分を展開図に書き込んでいきます。
見取り図で見える範囲はんいを展開図に書き込むと一番左の図になります。

ここからはなれた展開図の面をつないでいきましょう。
左から2番目の図に注目してください。

こちらの図の黄色の点線が見取り図の紫の矢印の部分と同じになります。

このように面と面が組み立つように考えていくと、赤い点線や緑の点線も使って、
一番右のように展開図を書くことができます。

わかみや先生

「立体図形」は文章だけでは完全に説明するのは難しいです。
もっとしっかり勉強したいと思っている受験生は、
ぜひ紙を使って展開図を作ってみてください！
グッと理解度が上がると思います！！

問題に挑戦ちょうせん！

図1は、直方体にひもをかけたときのようすを表しています。
このとき使ったひもの長さは結び目の12cmを入れて100cmでした。
これについて、次の問いに答えなさい。

① この直方体の高さは何cmですか。
② 図２のひもの線をかき入れ、結び目のところに○印を書きなさい。

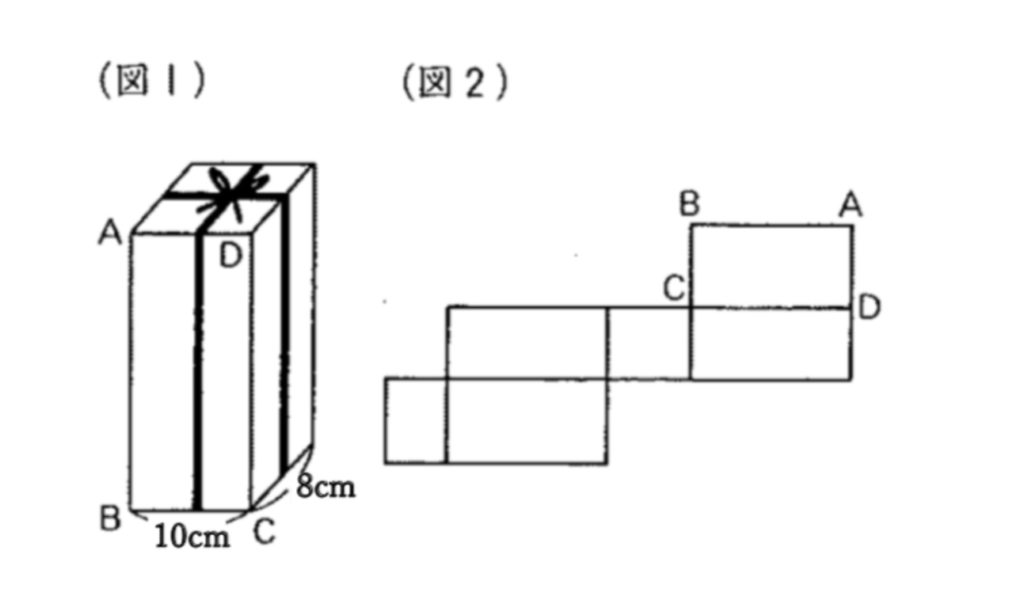
解答

答えを見るにはここをクリック！

①13cm
②図に書いてあります

この記事を書いている人はこんな人

解説を見てみよう！

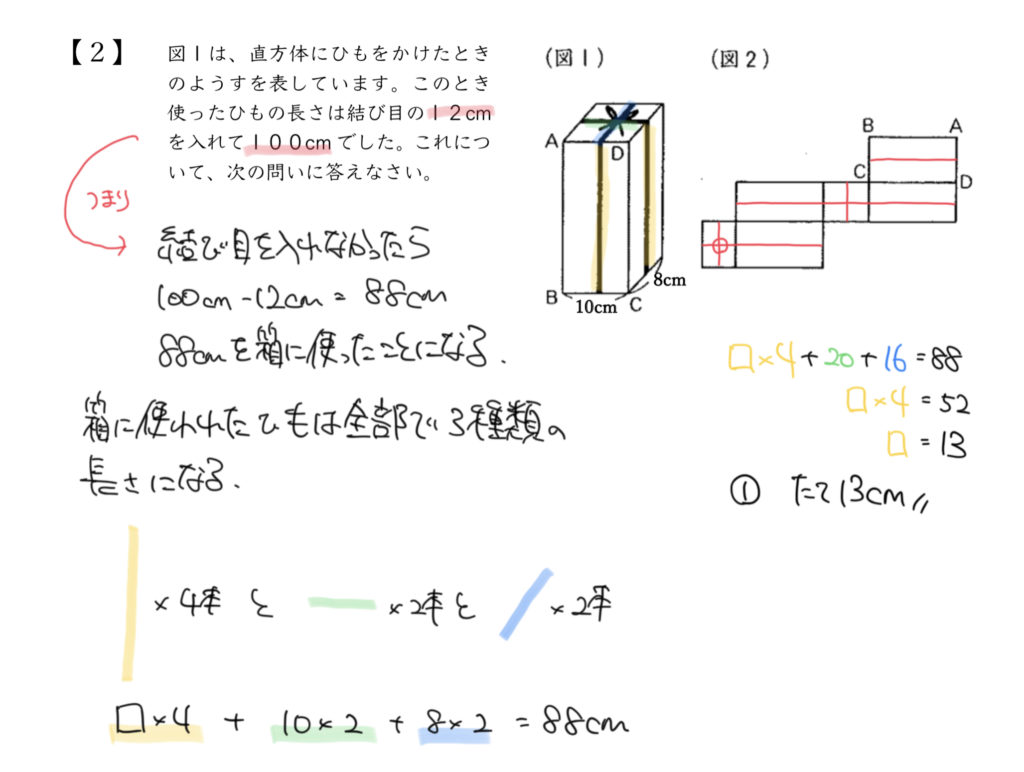
STEP1：見取り図全体を部分と部分に分けて考えよう

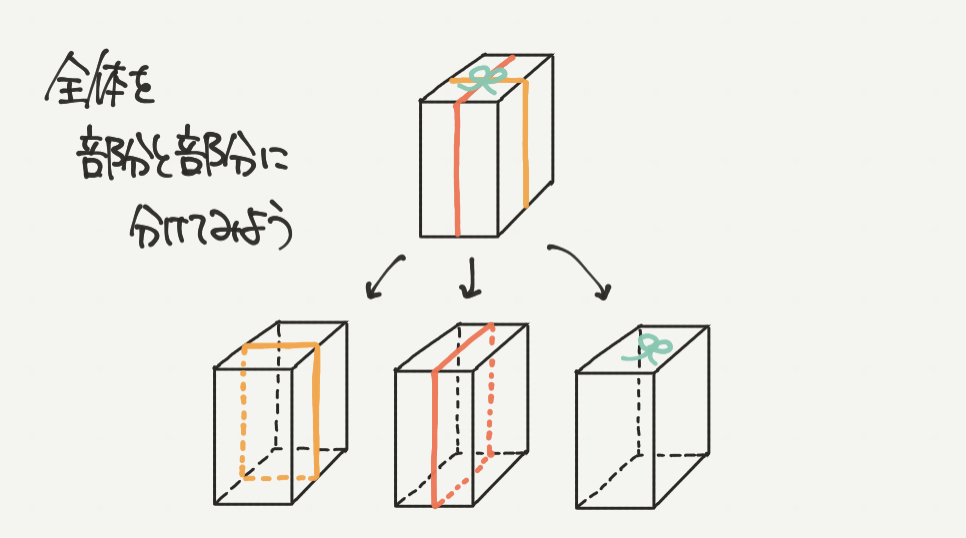
「さんすうがく」の中で大切な考え方の一つに「全体は部分と部分でできている」という考え方があります。

今回のひももよく考えると3つに分けることができます。
それが黄色のひも、赤のひもそして緑のリボンです。

全部をまとめてしまうとむずかしく考えてしまいがちですが、
1つ1つを分けて考えると少しはわかりやすくなると思います。

STEP2：それぞれのひもの長さを計算してみよう

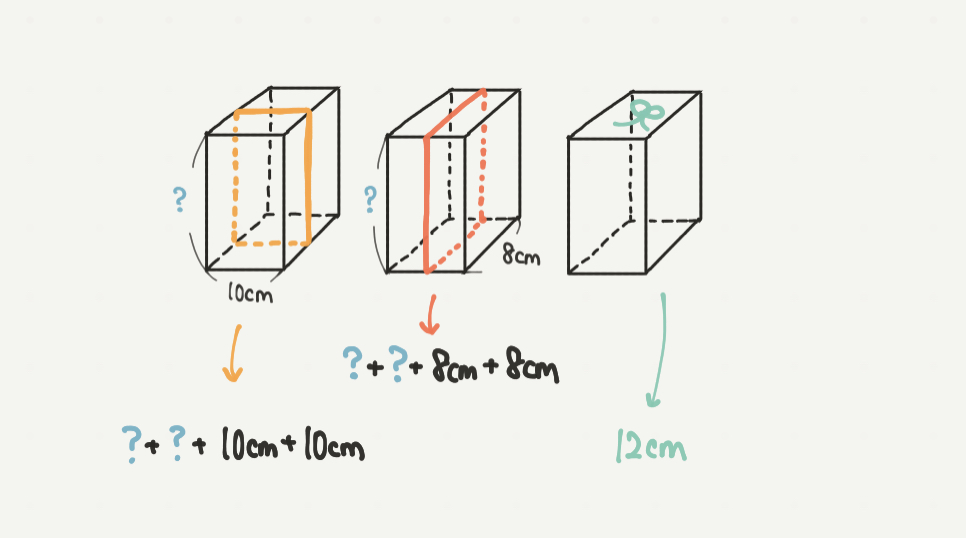
わからない高さの部分を？として、長さを求めていきましょう。

黄色：？+？+10cm+10cm
赤：？+？+8cm+8cm
緑：12cm（問題文に書いてありますね。）

見取り図にして考えてみると、ひもの長さを計算することがかんたんになります。

これらの合計の長さが100cmなのでSTEP3で？を求めましょう。

STEP3：合計の長さ100cmから？を求めよう

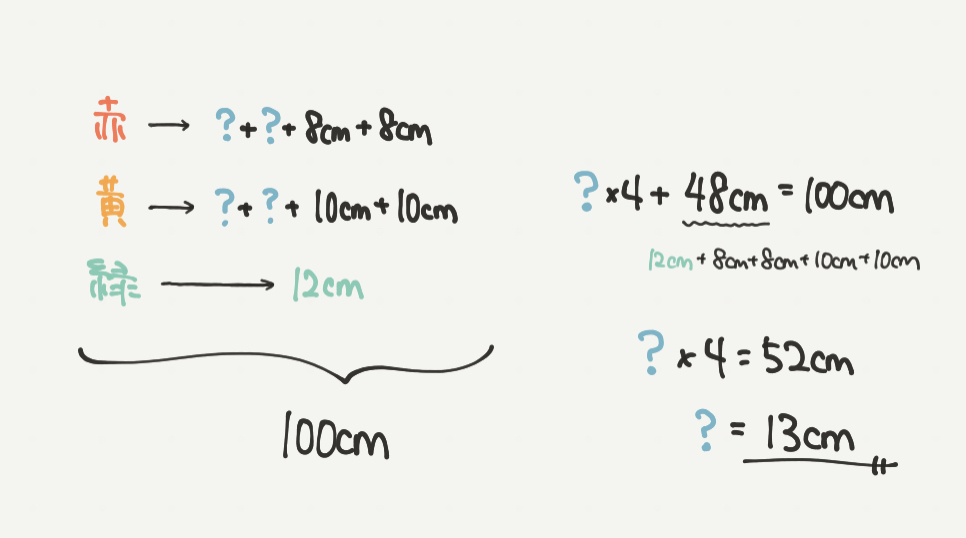
STEP1ではまとまったひもを一つずつ部分に分けて考えていきました。
STEP2ではそれぞれの長さを計算して？を使って表しました。

そしてそれぞれの長さの合計が100cmであることから？を求めましょう。

黄色：？+？+10cm+10cm
赤：？+？+8cm+8cm
緑：12cm

なので3つの合計の長さは、

？+？+？+？+10cm+10cm+8cm+8cm+12cm
=？×4+48cm

これが100cmと言われているので、
100cm=？×4+48cm
？×4=52cm
？=13cm

と計算することができました。

STEP4：見取り図から展開図に直していこう

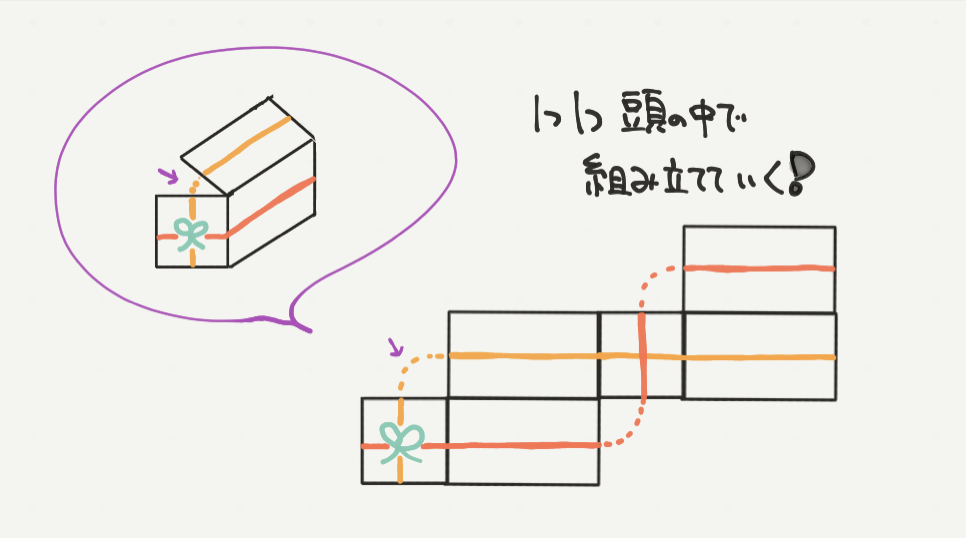
②の問題ははじめにで説明した通り考えてもらうとわかりやすいかと思います。

今回は基準きじゅんとなる面をリボンのついている面にして、わかるところを書いています。

頭の中で立体図を組み立てていき、紫の矢印につながるひもの場所を点線で書いていきます。

すると展開図のひもの長さが上図のように書けるはずです！

直方体にかけたひもの長さを求める問題のまとめ

今回の問題で大事なポイント

立体図形で大切な3つの言葉（はじめに）
・見取り図
・投影図
・展開図
見取り図から展開図への考え方（面がどことつながるのか考えよう！）
「全体は部分と部分でできている」考え方（STEP1）

ここまでが今回の「立体図形」の基本問題でした。
立体図形はやっぱり頭の中で組み立てるのはむずかしいですよね。
ていねいに解説を書きましたが、理解することができたでしょうか？

「立体図形」の問題を得意にするには、何度も説明していますが
実際に紙を使ってやってみることが一番だと思います。

一度紙を使って問題を解くと、次に問題を解くときに、
スッと頭の中で展開図を見取り図に組み立てやすくなります。