はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
今日は中学受験算数の速さについて、
苦手を克服するポイントを紹介させていただきます!
中学受験の算数の単元「速さ」はよく受験で出題されます。
速さは私たちの生活とかなり身近な反面、苦手とする学生が多いイメージがあります。
よく生徒で“き(きょり)・は(はやさ)・じ(じかん)”を使う方が多いですが、
それは覚えなくてもいい解法です。
なぜなら面積図の書き方さえ理解していれば時間と速さと距離の関係は問題ないからです。
「さんすうがく」では丸暗記に頼らないようにていねいに解説を書いていきますので、
しっかり学力を身につけていきましょう!
この記事を書いている人はこんな人


速さの問題でよく出る問題
- 旅人算
- 列車算
- 流水算
- 時計算
1:旅人算
旅人算ってなに?
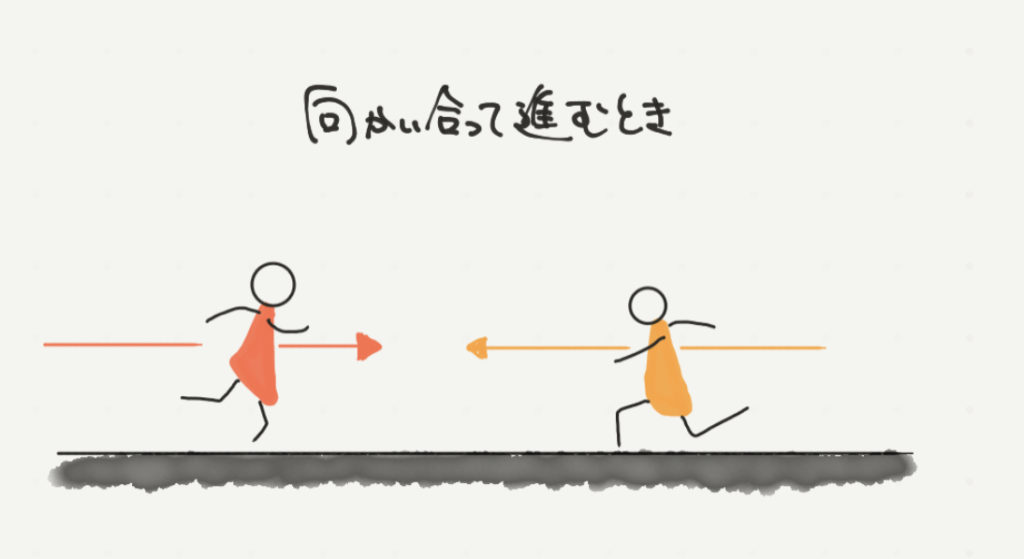

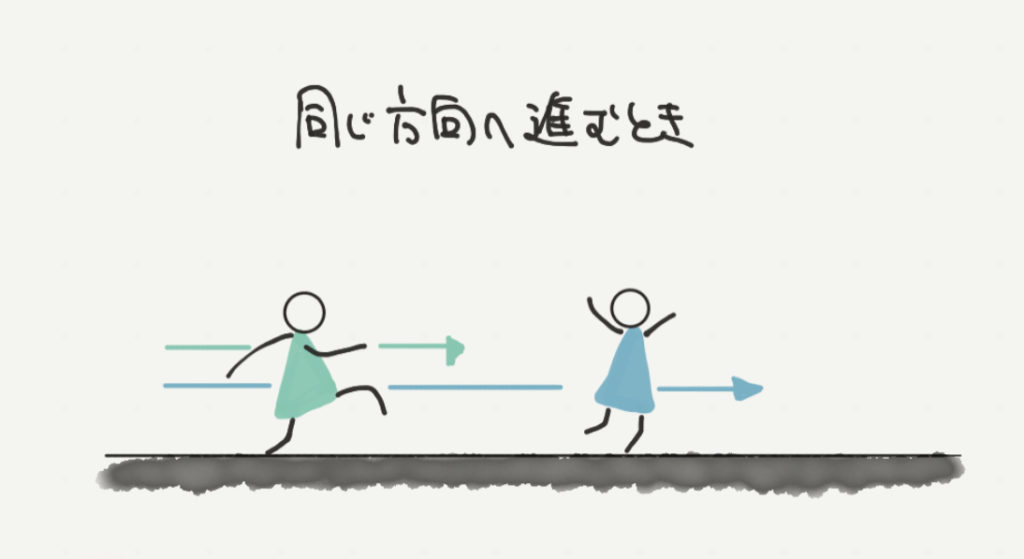

旅人算とは、違う速さで歩く人たちがいつすれ違うのか、いつ追い越されるのかを求めるような問題です。
出発する瞬間や、出会う瞬間、すれ違う瞬間など、場面場面を切り取って線分図でイメージして計算します
基本的に旅人算は以下の2つのパターンしかありません。
旅人算の解き方
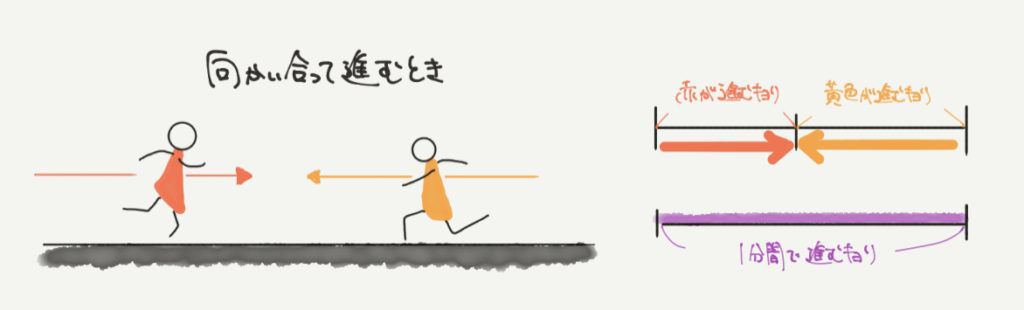

ふたりが向かい合って進むとき、ふたりは1分で紫(赤+黄色)の距離だけ近づくことになります。
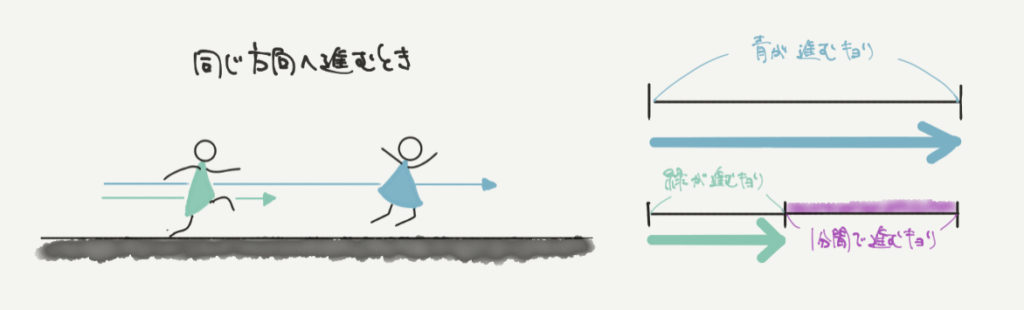

一方で二人が同じ方向に進むとき、1分間でお互いが近づくのは紫(青–緑)の距離になります。
それぞれ向かい合って進むときと反対方向に追いかけるときの具体的な問題は
すでに記事を作っておりますので、そちらを見てチャレンジしてみてください!




2:列車算
列車算の問題は問題文から、列車がどこからどこまでを走っていたのかをとらえることがポイントです!
列車が目の前を通過したとき
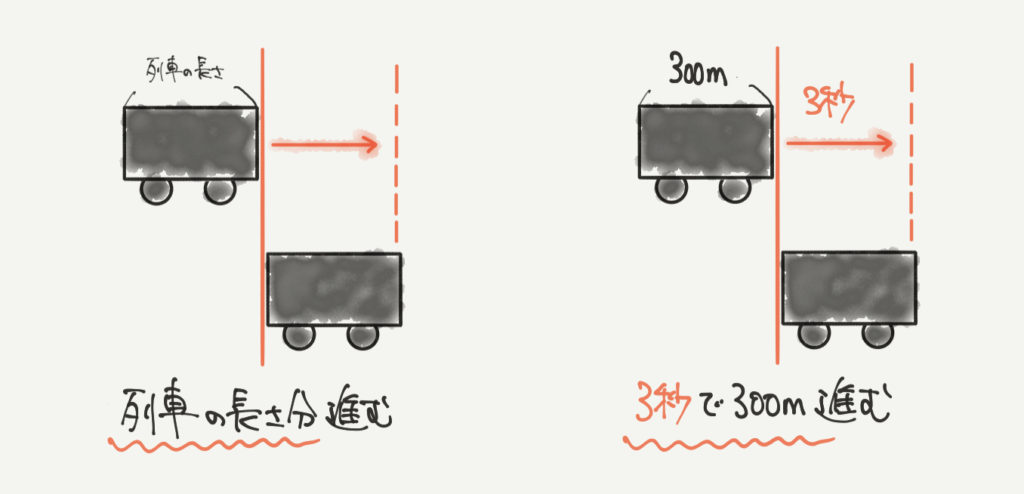

列車が目の前を通過したとき、列車は列車の長さ分だけ前に進みます。
たとえば300mの列車が目の前を3秒で通過したとき、
この列車は3秒で300m進むということになります。
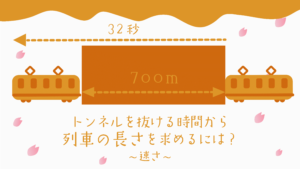
列車がトンネルを通過したとき
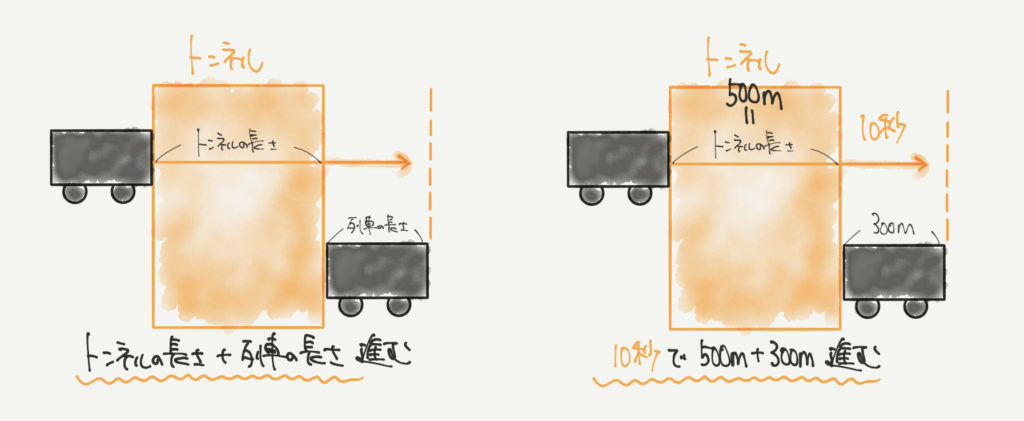

列車がトンネルを通過したとき、列車はトンネルの長さ+列車の長さ分だけ前に進みます。
たとえば300mの列車が500mのトンネルを10秒で通過したとき、
この列車は10秒で800m進むということになります。
列車がトンネルに入ってから出始めるまで
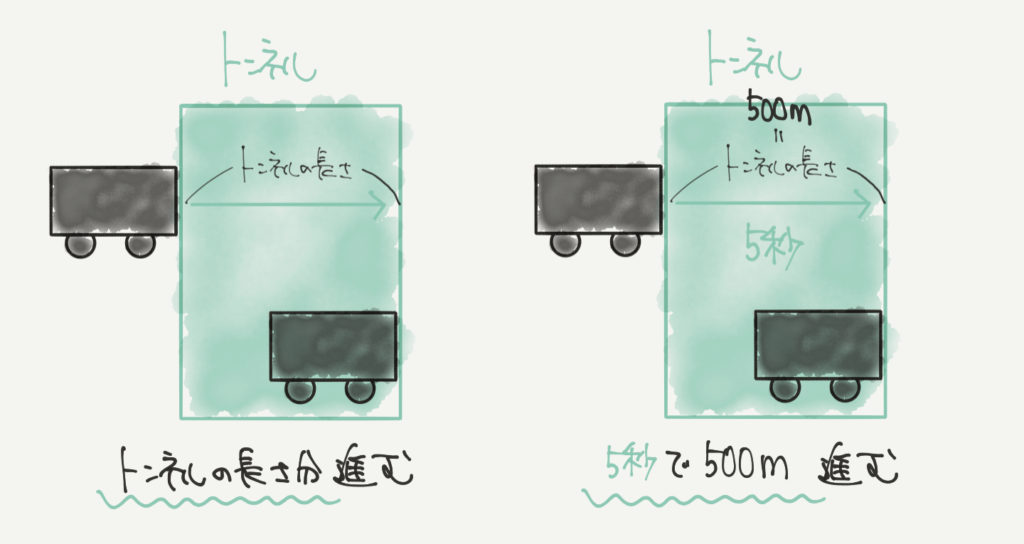

列車がトンネルを入ってから出始めるまで進んだとき、列車はトンネルの長さ分だけ前に進みます。
たとえば列車が500mのトンネルに入り始めてから5秒後に出始めたとき、
この列車は5秒で500m進むということになります。
列車がトンネルに入り終わってから出始めるまで
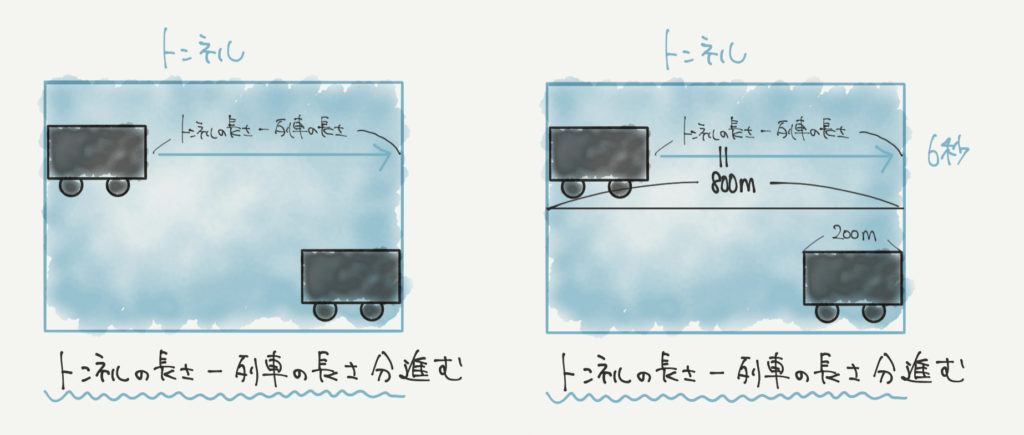

列車がトンネルを入り終わってから出始めるまで進んだとき、列車はトンネルの長さ分–列車の長さ分だけ前に進みます。
たとえば200mの列車が800mのトンネルに入り終わってから出始めるまでに6秒かかったとき、
この列車は6秒で600m(800m-200m)進むということになります。
列車算はこの進む距離さえきちんと捉えることができれば、列車算を攻略することができます!

3:流水算
流水算で大事なのは川の速さ


流水算の問題は、川の流れが出てくる問題になってきます。
まずはその川の流れについてのかんたんに説明しますね。
まず川は雨が降ることによってできます。
山に雨が降り、その雨が集まって川になります。
ここで覚えておいて欲しいのは、川は上から下に向かって流れているということです。
この川の上の部分を上流、下の部分を下流と言います。
流水算の問題ではこれらの知識を頭に入れておきましょう。
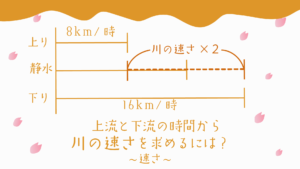
速さの線分図を書いておこう
流水算は川やプールなど、自分以外のものが流れている時に使われます。
自分たちの速さ以外に川やプールの速さを考えないといけないのがポイントです。
また流水算では流れに沿って進むのか、逆らって進むのかで速さが変わってしまうので必ず速さの線分図を書くことが重要です。
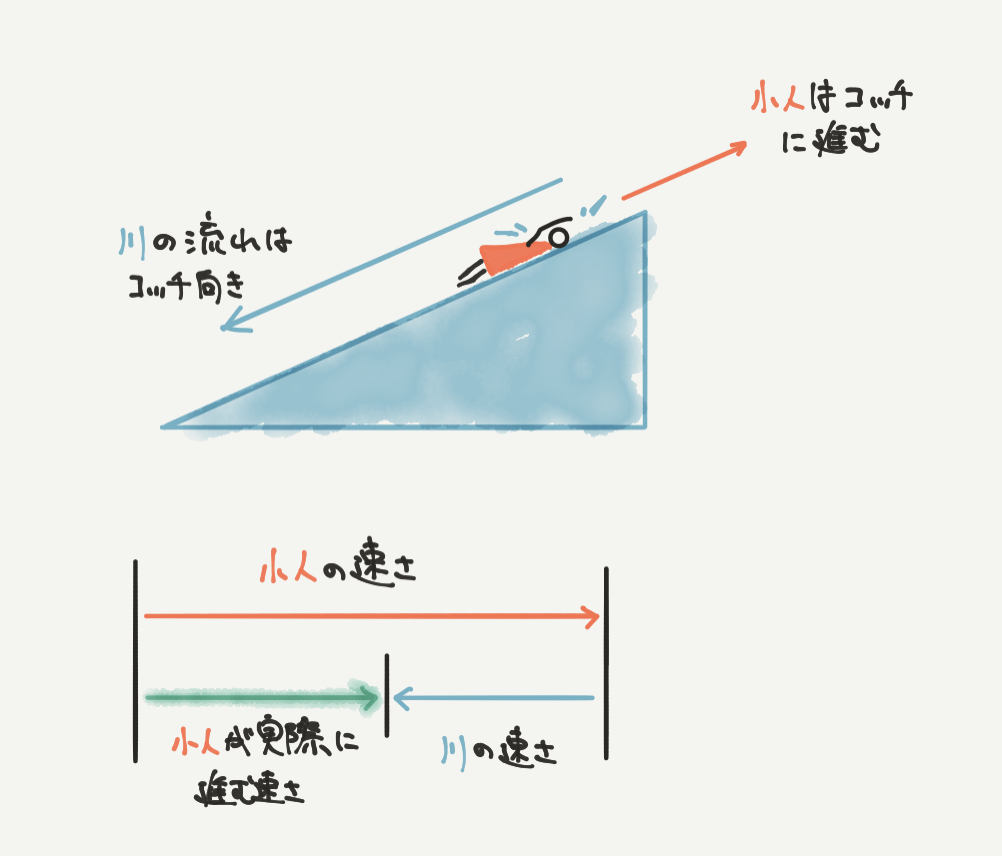

流水算の問題では、船がどの方向に進むのかによって速さが変わります。
たとえば、上の図では赤い小人が川の上流に向かって泳いでいます。
でも川の水は上から下に向かって進みます。
なので赤い小人の実際に進む速さは、
小人の速さ-川の速さとなります!
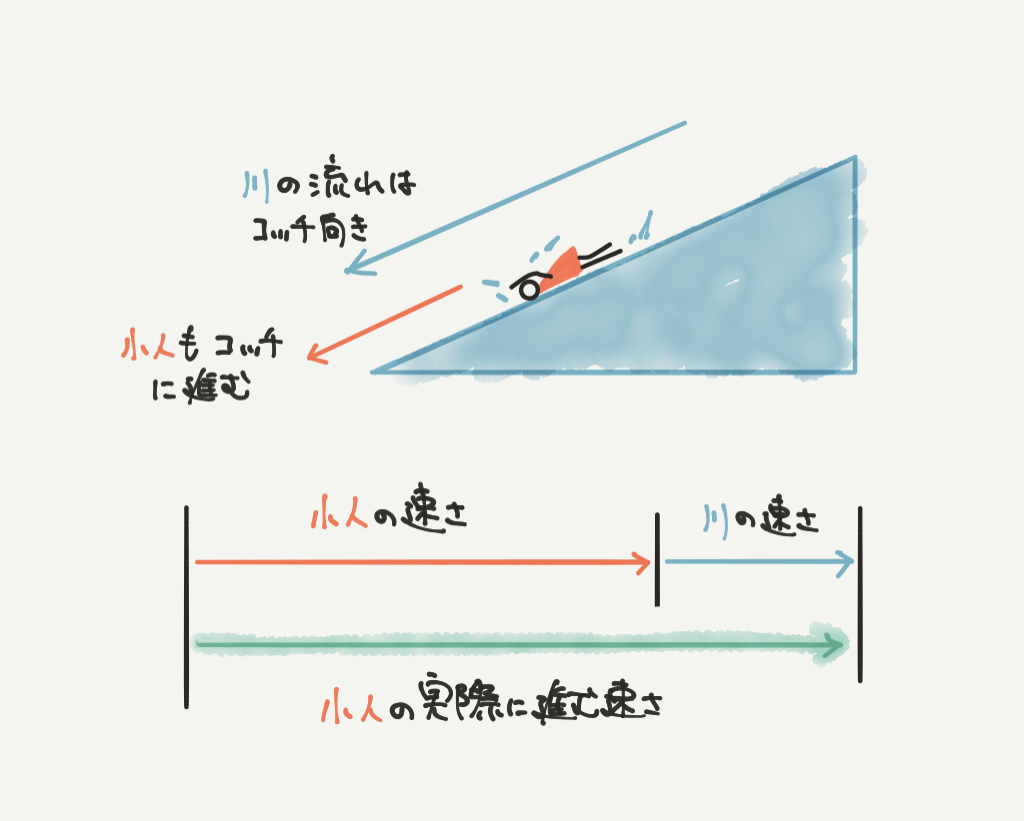

逆にこちらは赤い小人が下流に向かって進むときの図です。
このとき赤い小人の実際に進む速さは、
小人の速さ+川の速さとなります!
このように、小人が進む方向によって計算で計算する速さが変わってきますので注意しましょう!

4:時計算
時計には長い針と短い針がある


時計算の問題では2つの針が出てきます。
長針:時計の長い針のこと
短針:時計の短い針のこと
この長針と短針を使って問題を解きます。
長針と短針の進む速さを求めよう
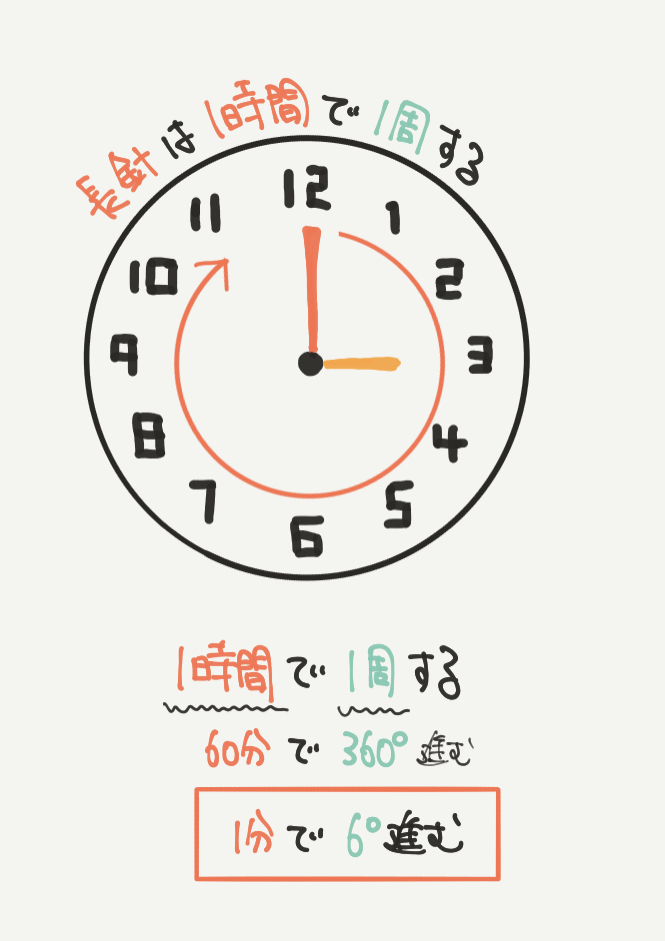

時計の長針は1時間で1周します。
なので1時間で360°進むことがわかります。
よって長針が1分間で進む距離は6°とわかります。
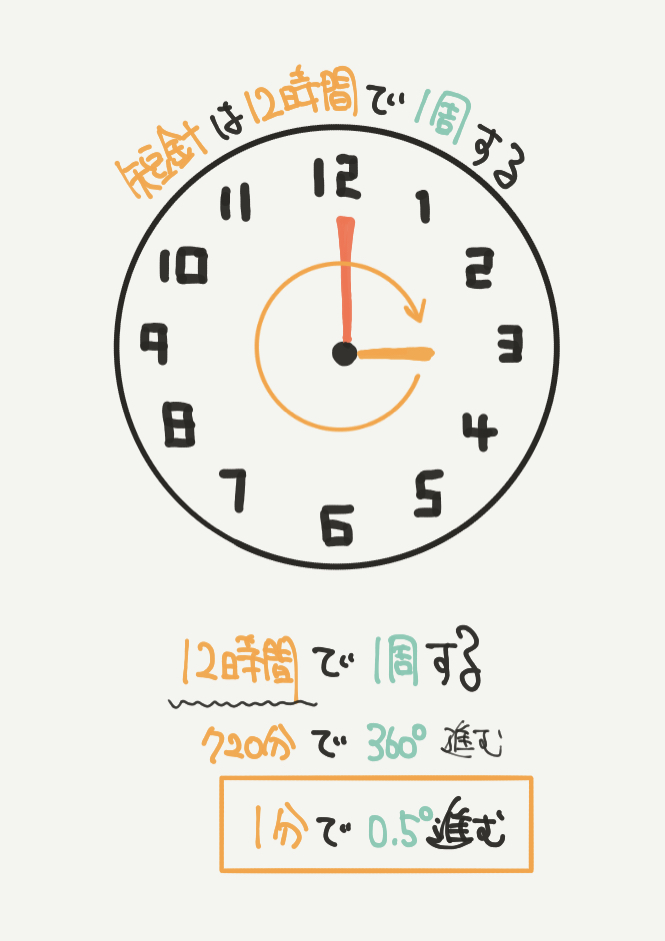

逆に、時計の短針は12時間で1周します。
なので12時間で360°進むことがわかります。
よって短針が1分間で進む距離は0.5°とわかります。
時計の数字の間の角度は30°
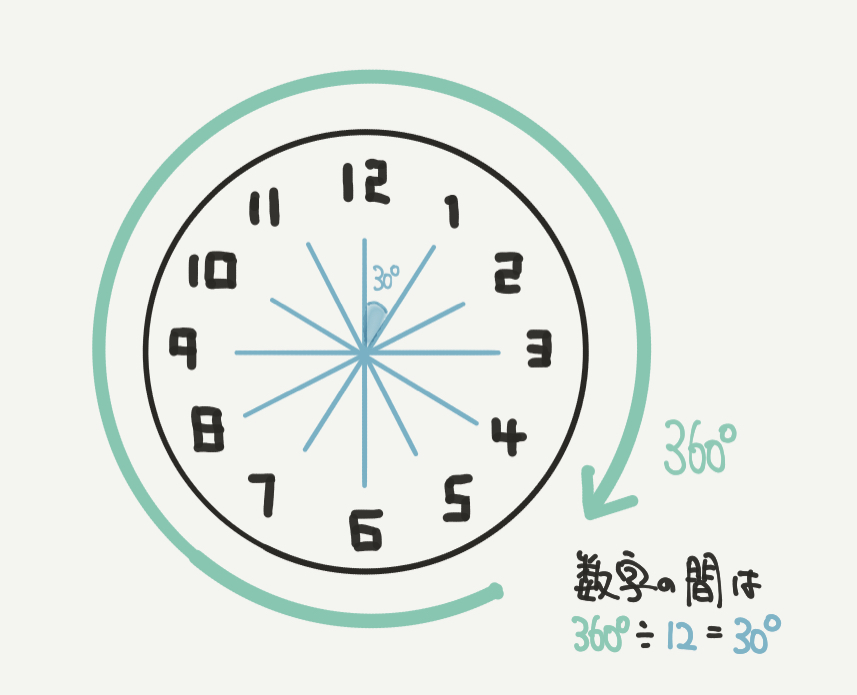

最後に時計の角度について確認しておきましょう。
1周が360°の時計で数字が全部で12個ありますので、数字と数字の間の角度は
360°÷12=30°となります。
ここまでが時計算で絶対に知っておいてもらいたい基本情報でした。
時計算ではこの基本を覚えておくと問題がスムーズに解けるようになります!!
実際に解いてみましょう!


速さの問題を得意にする4つのポイントのまとめ
速さの問題の4つの重要なポイント(復習)
- 旅人算
登場する人物たちの近づく距離を捉えよう!
向かい合って進むときと反対方向に進むときの距離を線分図で表そう! - 列車算
列車が進む距離を捉えよう!
列車が通り始めてから、通り過ぎてから、通り過ぎ終わるまでか、問題文をしっかり読もう! - 流水算
川の流れによって速さが変わる!速さの線分図を書いて計算ミスをなくそう! - 時計算
時計の長針と短針が進む速さを計算してみよう!
時計の間の角度を計算しよう!
全ての速さの問題に共通して言えることは他の単元より想像しやすいということです。
必ず頭の中でイメージしながら図を書くようにしましょう!!






