はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
今日は中学受験算数の平面図形に関する問題についてのポイントを
紹介させていただきます!
中学受験では「平面図形」と「立体図形」の問題がよく出題されます。
平面図形はなんとなくわかるけど、立体図形が苦手という方も多いのではないでしょうか?
平面図形は1つの単元としても重要ですし、この記事の後に勉強する立体図形の単元の基礎にもなります。
また、平面図形の問題は中学入試だけではなく、高校入試にも頻繁に出題される問題です。
「平面図形」「立体図形」が苦手な受験生にこそ、この記事の説明を見ていただきたいです。
ていねいに説明していますので、一緒に勉強していきましょう!
この記事を書いている人はこんな人


平面図形で重要な解法
平面図形に関する問題の4つの重要なポイント
- 角度の知識
- 等積変形
- 補助線
- 図形の知識
この記事では上の4つのポイントについて解説しています!
①角度の知識
平面図形でこれだけは覚えよう!角度の知識①
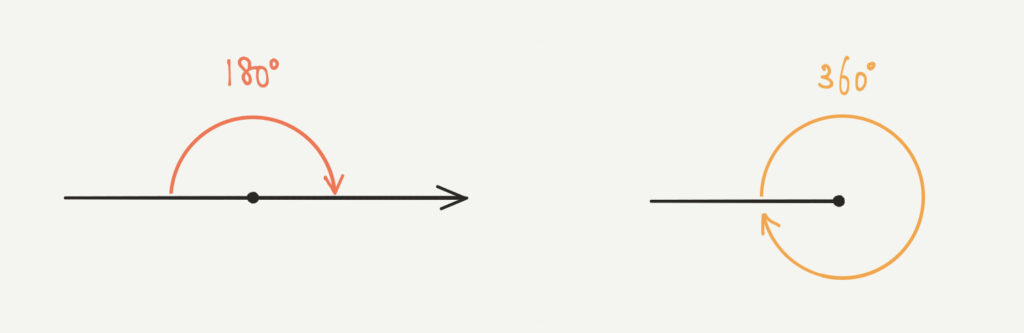

まずは「角度の知識」から1つ1つ勉強していきましょう。
一周は全部で360°、半周は180°です。
平面図形でこれだけは覚えよう!角度の知識②


またこのスリッパ型の角度も頭に入れておきましょう。
このスリッパのような形を見つけたら、図のaとbとcの角度に注目しましょう。
このときこちら式が成り立ちます。
c=a+b
三角形の2つの角(aとb)が、外角の和(c)と等しくなっています。
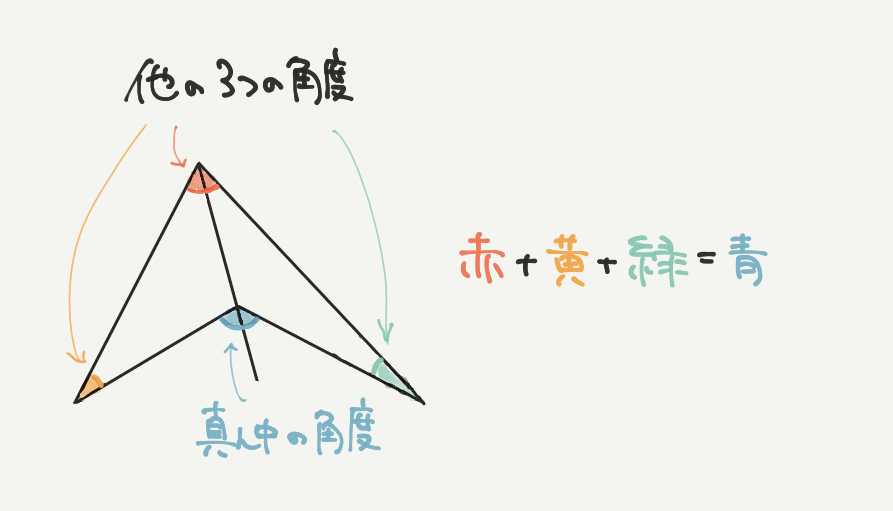

そしてこのスリッパの応用が上の図です!
スリッパを2つ重ねるとこのような式ができます。
赤+黄+緑=青
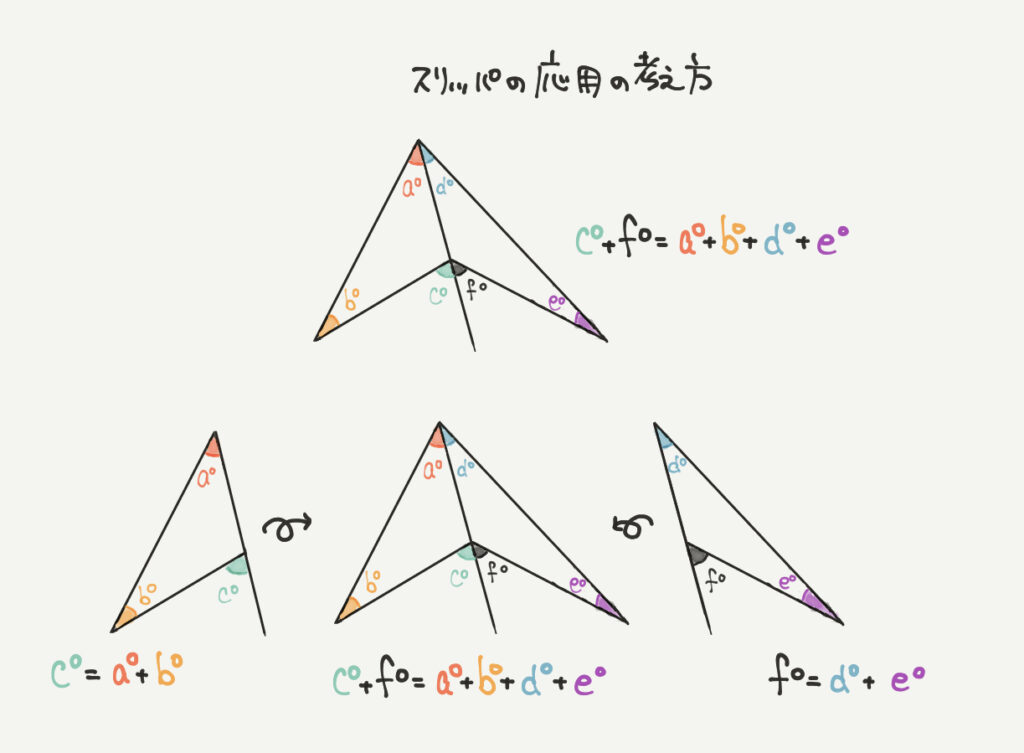

a+b=c
d+e=f
のそれぞれのスリッパを合わせると、
c+f=a+b+d+eとなります。

平面図形でこれだけは覚えよう!角度の知識③
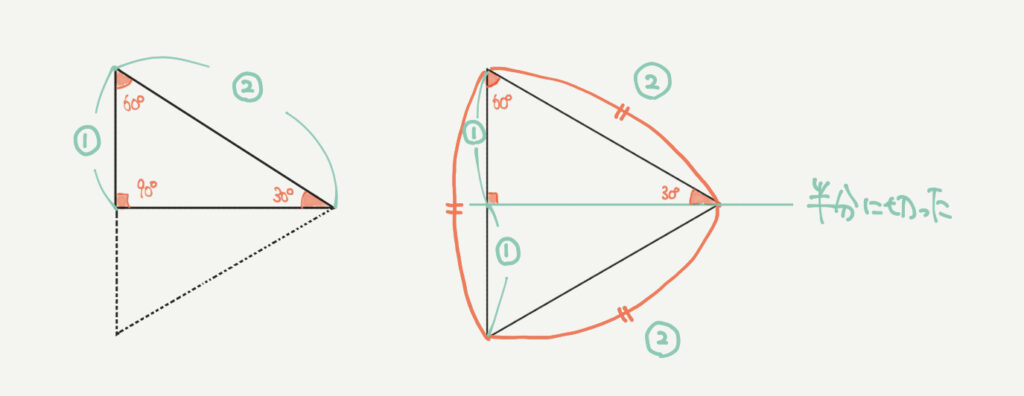

また角度が30°60°90°の三角形のとき、三角形の斜めの長さと横の長さの比が2:1になります。
これは同じ角度の三角形を2つ重ねると、正三角形を作ることができます。
正三角形は全ての辺の長さが同じなので、1辺を②とすると、全部の辺の長さが②となります。
30°60°90°の三角形は正三角形の半分なので、横の長さは①になります。
ここから斜めの長さと横の長さが2:1になります。

②等積変形


図形を解く上で重要なポイントがこの後説明する「補助線」と「等積変形」です。
等積変形とは漢字の通り、等しい面積を変形させることです。
この等積変形を成立させるためにはいくつかの知識が必要です。
この例を見てみましょう
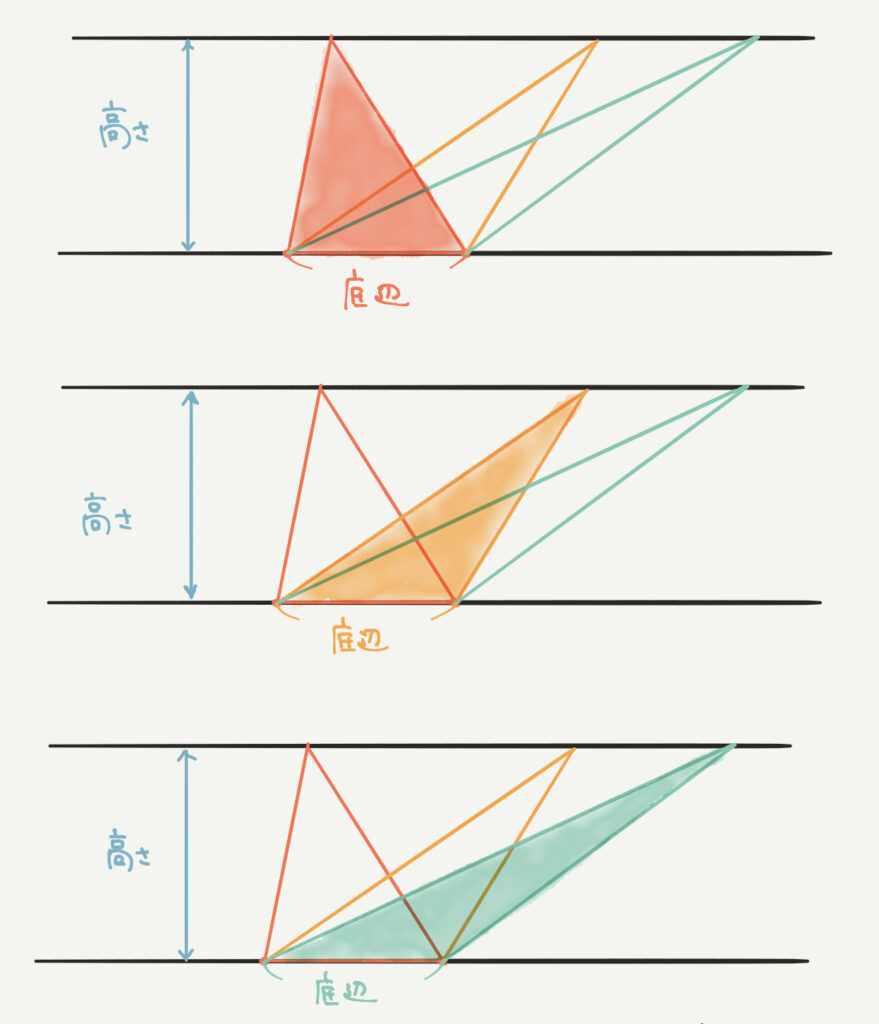

三角形の面積は底辺×高さ×1/2です。
つまりこの図にある赤と黄と緑の三角形は底辺も高さも同じなので、どの三角形も同じ面積になります。
赤の三角形:底辺×高さ×1/2
黄の三角形:底辺×高さ×1/2
緑の三角形:底辺×高さ×1/2
※底辺と高さの値が今回同じ!
このようなとき図形を図形を移動させることができ、それを等積変形と言います。





③補助線
「等積変形」と同じくらい重要なのが「補助線」に関する考え方です。
この補助線をしっかりひけないと「等積変形」がうまくできず解くのが困難になってしまいます。
補助線を引く明確なルールは存在しませんが、
補助線をひくときのポイントは
見慣れていない形から知っている形にすることです。


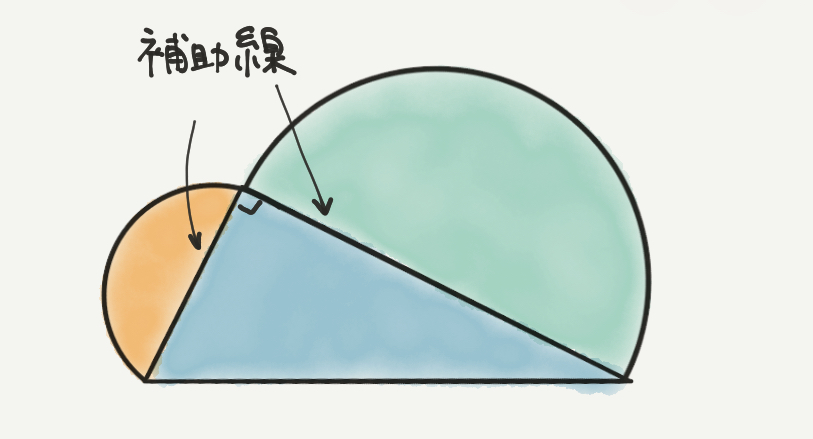
例えば上の図形の面積を求めたいとします。
パッとみたとき全然分からなさそうな図形ですが、
補助線を引けば少しずつ解き方が見えてくると思います。

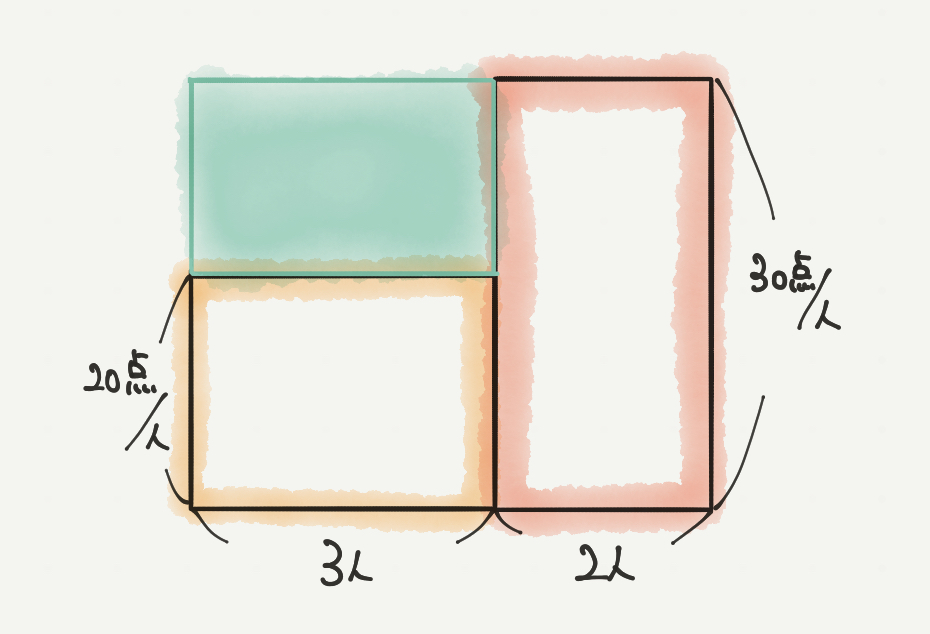
他にも、「平面図形」の単元ではありませんが、
「和と差に関する問題」の解き方の中で面積図を書きましたが、
実はこの面積図の中でも何回か「補助線」を使っていました。
面積図の補助線の例



④図形の知識
平面図形攻略!① 外角の和は必ず360°


図形の外角は、上のような三角形、四角形、五角形の青色の角度のことです。
三角形であれば外角は3つ、
四角形であれば外角は4つ、
五角形であれば外角は5つ、
と増えていきます!
よって⚪︎角形の外角は全部で⚪︎個になります!
これらの外角の和は必ず360°になる、という点を覚えておきましょう!!
平面図形攻略!② 対角線の本数の求め方

ある図形から引ける対角線の本数の求め方も、ここで勉強していきましょう!
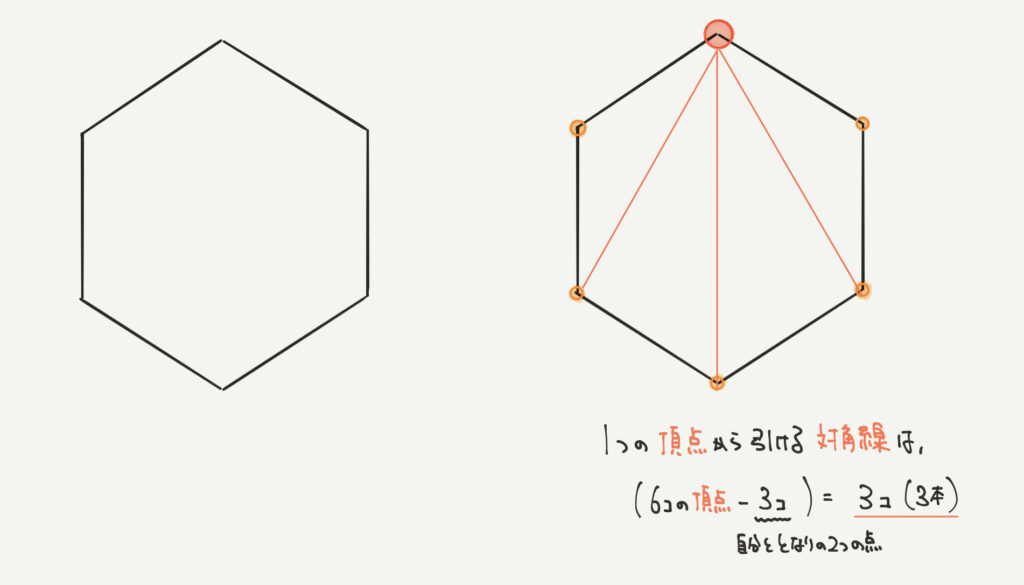
今回は六角形を例に対角線の本数を求めていきます。
1つの頂点から引ける対角線の本数は、6本–3本=3本となります。
※3本=頂点の数6個–自分と隣の2つの点
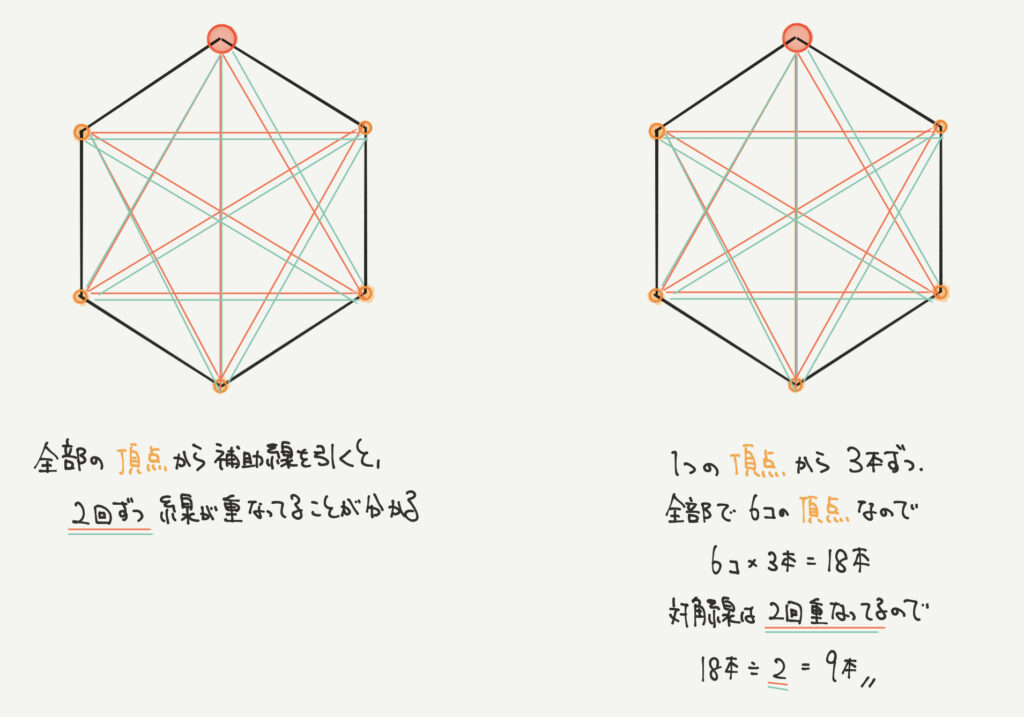

1つの頂点から引ける線は3本。
頂点は全部で6個あるので、3本×6個=18本の線が引けます。
対角線の本数を見ていると、全部で2回ずつ線が引けることがわかります。
よって対角線の本数は18本÷2回=9本となります。


平面図形攻略!③ 台形の求め方
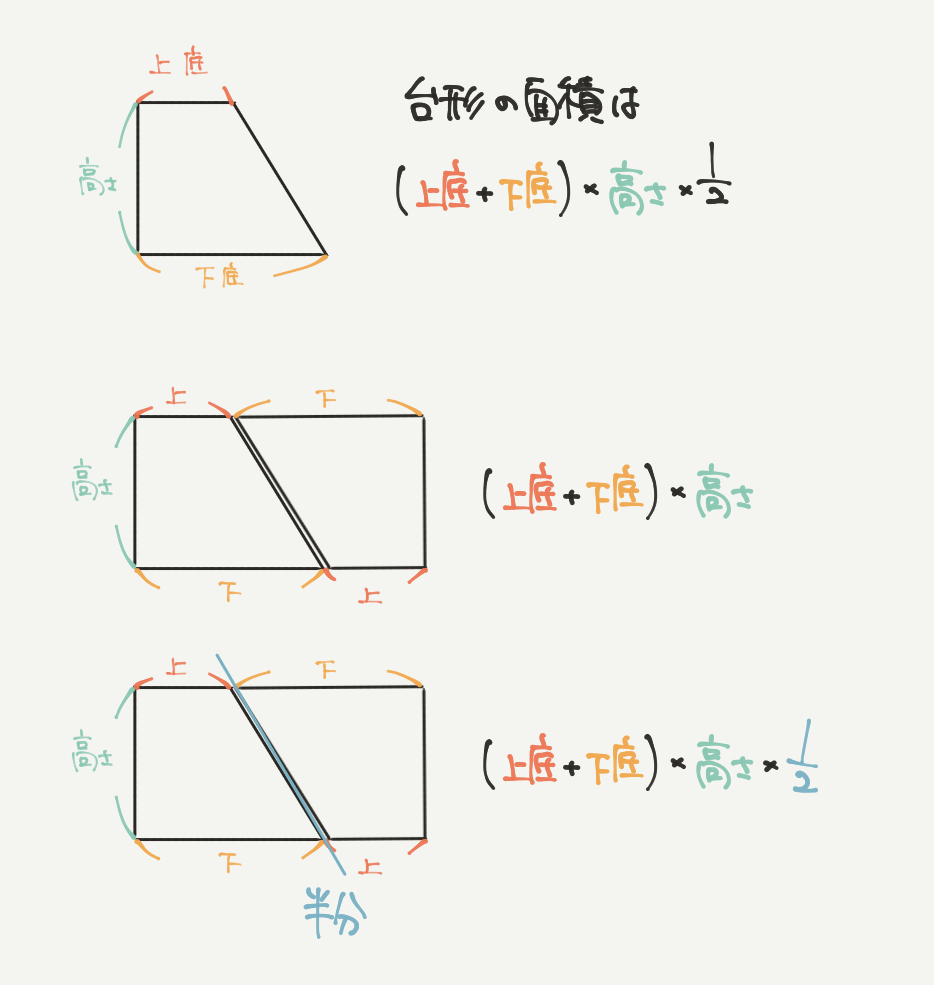

台形の面積の求め方についてもここで復習しておきましょう!!
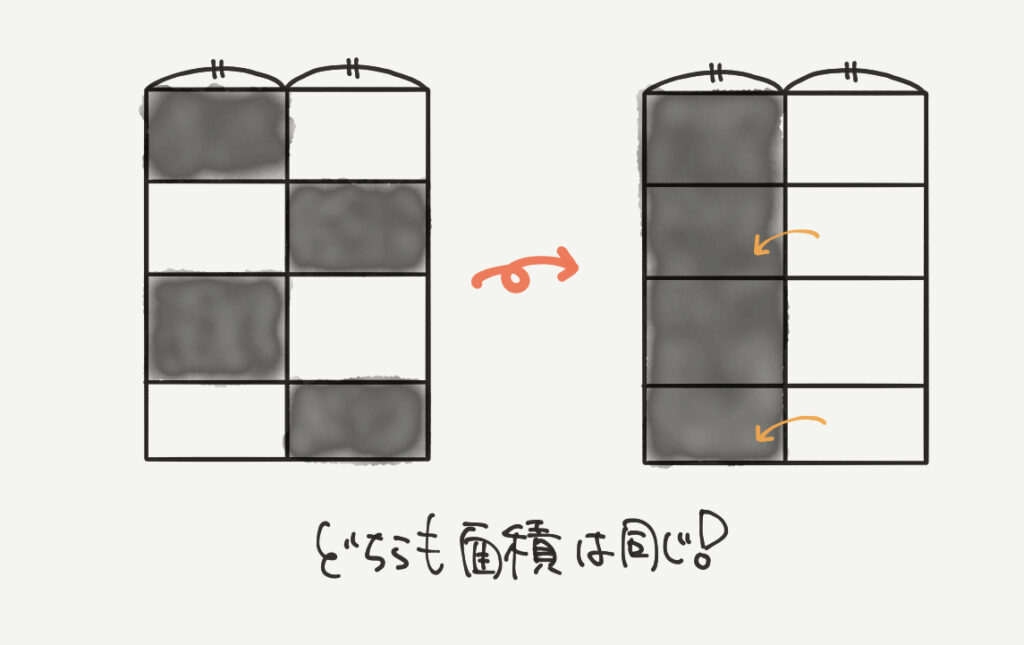
台形の面積は、大きな四角形を作って半分にする求め方が一般的です。
台形を逆さまにしてつなげると、(上底+下底)×高さの大きな四角形が作れますね。
求めたい台形はその半分なので、
台形=(上底+下底)×高さ×1/2、となります。
平面図形攻略!④ ひし形の求め方
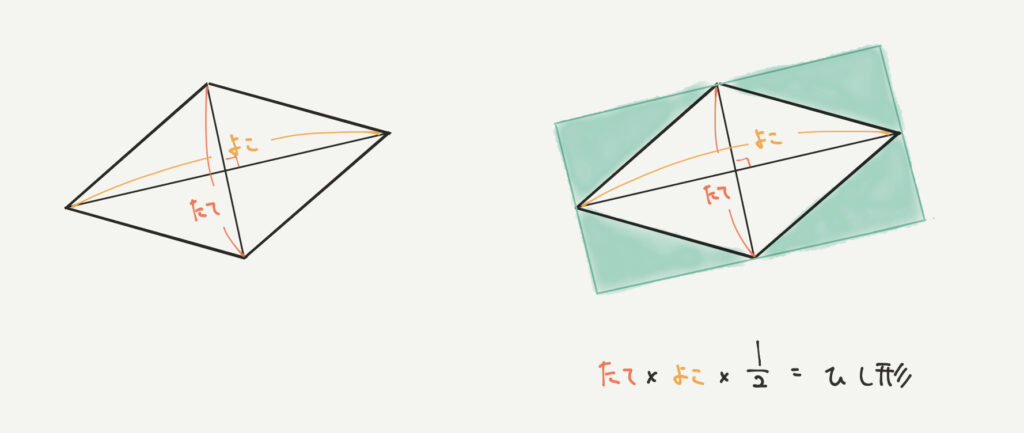

ひし形は対角線の角度が90°になる四角形のことです!
このひし形の面積も大きな四角形を半分にするやり方で求めていきましょう。
たて×横=緑の大きな四角形
ひし形=緑の大きな四角形の半分(1/2)なので、
ひし形=たて×横×1/2となります。
平面図形攻略!⑤ 内角の求め方
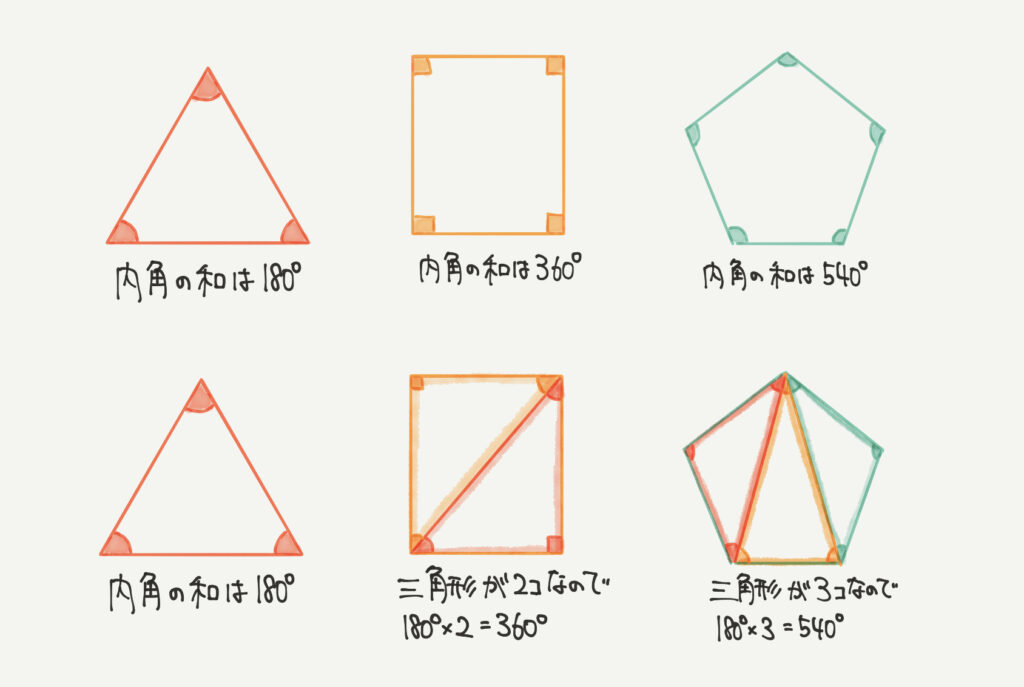

最後は多角形の内角の和についてです。
三角形の内角の和=180°ということだけ頭に入れておきましょう!
すると三角形の内角の和=180°。
四角形は補助線を引くと三角形が2個作れるので、内角の和が180°×2個=360°。
五角形は補助線を引くと三角形が3個作れるので、内角の和が180°×3個=540°。
このように補助線を引くことで多角形の中に三角形を作ることができます。
多角形の内角の和も基本的には補助線を使って求めていきましょう!

平面図形の問題を得意にする4つのポイントのまとめ
平面図形の問題の4つの重要なポイント(復習)
- 角度の知識
- 等積変形
- 補助線
- 図形の知識
この内容だけ見ても頭は良くなりません。
ちゃんと上の4つのポイントを意識しながら問題に挑戦していくことが大切です。
「平面図形」ですが以上の4つの点を勉強してから問題に挑戦すれば
今までよりもかんたんに問題を解くことができると思います。
「角度の知識」や「図形の知識」など、覚えないといけないことも多くて大変だと思います。
問題演習を通じて、学習した知識を使ってみることが重要です。
この知識をきちんと理解できれば「平面図形」や「立体図形」の問題が圧倒的に解きやすくなるはずです!
これを読むだけですと、勉強した気になっているだけになってしまいますので、
実際に問題を解いてたくさん経験を積んでいきましょう!






