【中学受験算数を攻略】和と差に関する問題を得意にする5つのポイントを徹底解説！

はじめに

中学受験では「和と差に関する問題」はよく出題されます。
当たり前ですが、偏差値へんさちの高い学校ほど問題はむずかしくなります。

しかし偏差値へんさちの高いほとんどの学校はむずかしいことを受験生のみなさんには要求ようきゅうしていません。
受験では、いかに基本に忠実か？いかに式や計算を理解しているのか？を見ています。

「さんすうがく」ではこの「和と差に関する問題」を千里の道の第一歩として考えています。
時間に余裕よゆうのある受験生は問題を解く前にこの記事のポイントを一つ一つ確認しておきましょう。

この記事を書いている人はこんな人

和と差に関する問題で重要な解法

和と差に関する問題の5つの重要なポイント

• 線分図と面積図の書き方
• 図の書き分け（面積図と線分図のどっちを書くか？）
• 比の考え方
• ベン図について
• 仕事量の仮定
  
  この記事では上の5つのポイントについて解説しています！

①線分図と面積図の書き方

この線分図、面積図は「さんすうがく」でもたくさん使われる解法です。
基本的きほんてきに算数の問題はこの2つのやり方で解答にたどり着くことができます。

なんにために図を書くのだろう？

そもそも、線分図や面積図を書いて問題を解くのはなんででしょう？

それはケアレスミスを防止するためです。

受験生のミスで一番多いのは、頭の中だけで計算してしまってケアレスミスをしてしまうパターンです。
そして残念ざんねんなことに成績の低い受験生の方が式だけ、頭の中だけで計算してしまう傾向けいこうがあります。

このような小さなミスをなくすためにまずは騙だまされたと思って図を書くようにしてみましょう。

線分図ってなに？

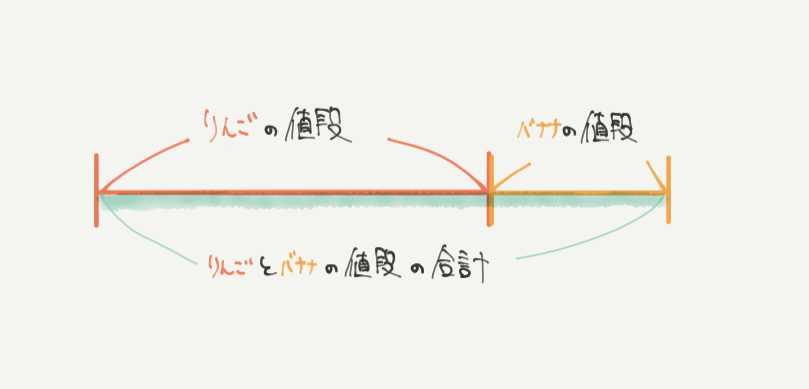
線分図とは、横に線をのばしてあるものとあるものを比べたり、足したりするときに使います。
この図ではリンゴの値段とバナナの値段を足して、合計金額を緑色で表しています。

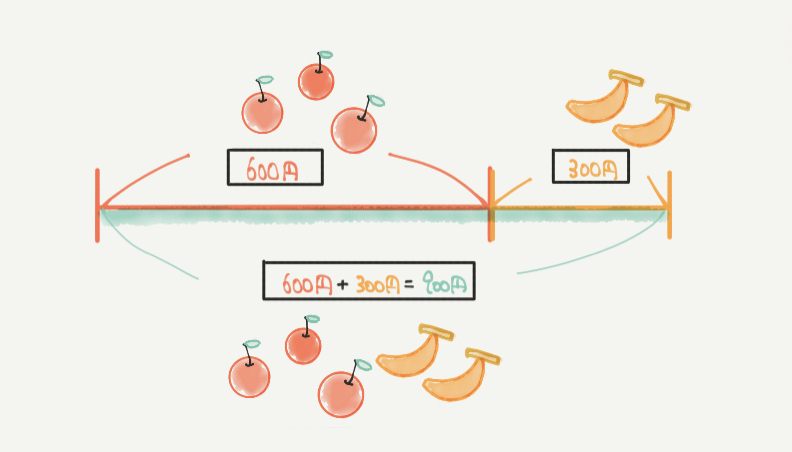
たとえば、この図ではリンゴ3つのお金（600円）とバナナ2本のお金（300円）をたすと900円になりますね。
こういうとき、線分図を使って書くとわかりやすく考えることができます。

面積図ってなに？

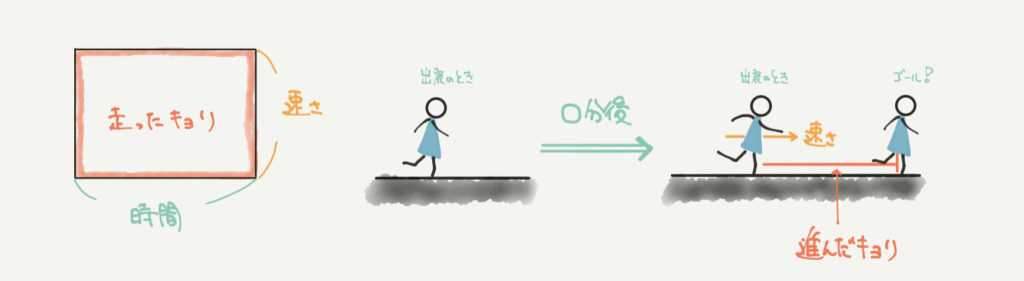
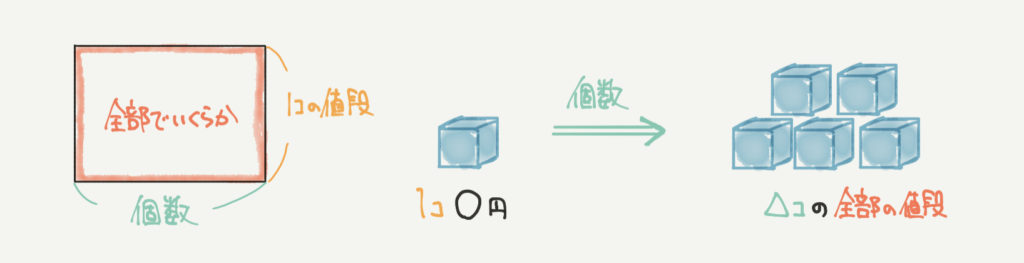
面積図とは、四角形の性質（たて×横）を使って問題を解くようなやり方です。

1個で●円のものが○コある、とか1時間●m進む車が○時間進むといった問題を理解するときに役に立つポイントです。
たとえば、下の図では1分あたり60m進む青い小人が5分間歩いたときの進んだ距離きょりの合計（300m）を表しています。

↑③図の書き分けでくわしく説明します！

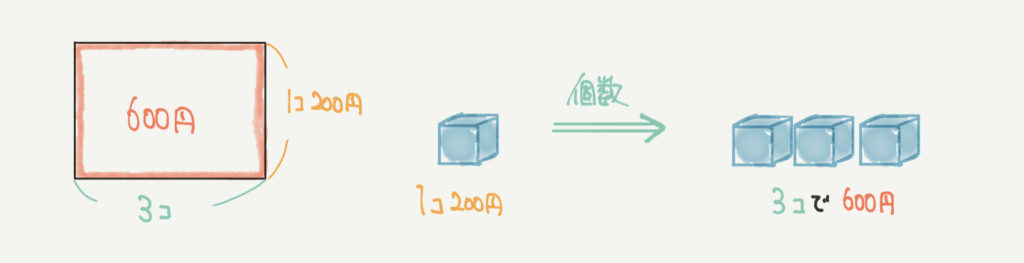
もう一つ、たとえば下の図では1個200円のものを3個買ったときの値段（600円）を求めています。

見直しするときにその式に書かれている数字の意味まで見直す受験生はほとんどいないと思います。

そうすると、式だけ書いてしまうだけで本当は見直していないのに見直した気になってしまうといった可哀想かわいそうなことがおきてしまいます笑　

必ず線分図や面積図を書いて、本当にその数字まで正しいのか確認するようにしましょう！

②図の書き分け（面積図と線分図のどっちを書くか？）

じゃあどういうときに面積図を書くのか？どういうときに線分図を書けばいいのか？

受験生のみなさんも同じように疑問ぎもんに思うかもしれません。
受験生だったときの私もどういうときに図を書き分ければいいのかわかっていませんでした。

面積図を書くときはどういうときが多い？

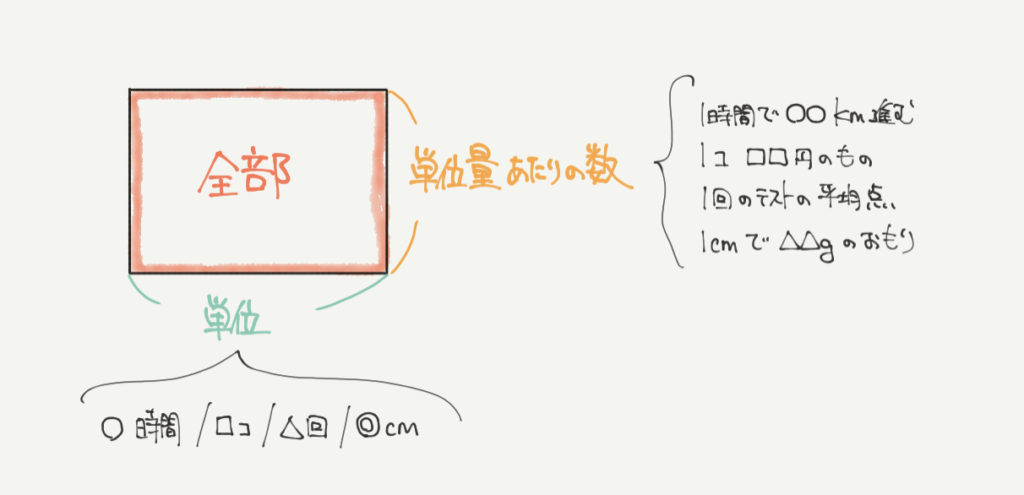
面積図を書くときは「単位量たんいりょうあたりの数字が出てきたとき」が多いです。

「単位量たんいりょうあたりの数字」とは、時速○km（1時間で○km進む）や1個あたり○円、
1部屋あたり何人かなど、ある単位に対して数字が決まっているときです。

図のようにたての辺に「単位量たんいりょうあたりの数」、横に「単位」と書くことができます。
面積図は「たて×横」で計算できるときに使うと解きやすくなります！

線分図を書くときはどういうときが多い？

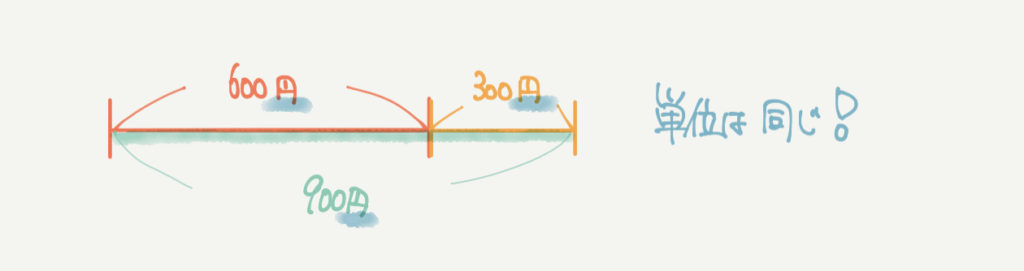
たとえば上の図では600円＋300円＝900円と単位が同じになっていますね。
線分図を書くときはこのように、同じような単位を使って計算するときに解きやすくなります。

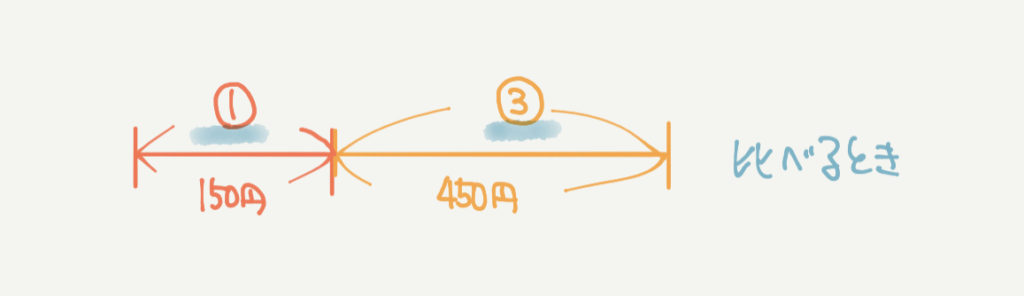
線分図を使うときは単位が同じときと説明しましたが、それに加くわえてなにかを比べるときにも線分図を使います。
上の図では2つの金額を150円、450円と書いているだけでなく、比を①と③と書いて比べています。

↑この比の考え方については次で説明しています！

面積図は「単位量たんいりょうあたりの数」が出てくるとき、
線分図は「単位は同じとき」「単位が同じものを比べるとき」って考えればやりやすそうですね！

③比の考え方

②図の書き分けでも少し説明しましたが、そもそも「比」とはなんでしょう？
比とは何かと何かを比くらべているわけですから、どれくらい２つの数が違ちがうのかを比くわべているということになります。

和と差に関する問題ではどこを基準きじゅんに他と比べるのかが重要になってきます。

↑この基準を定めることを「仮定する」と言います。

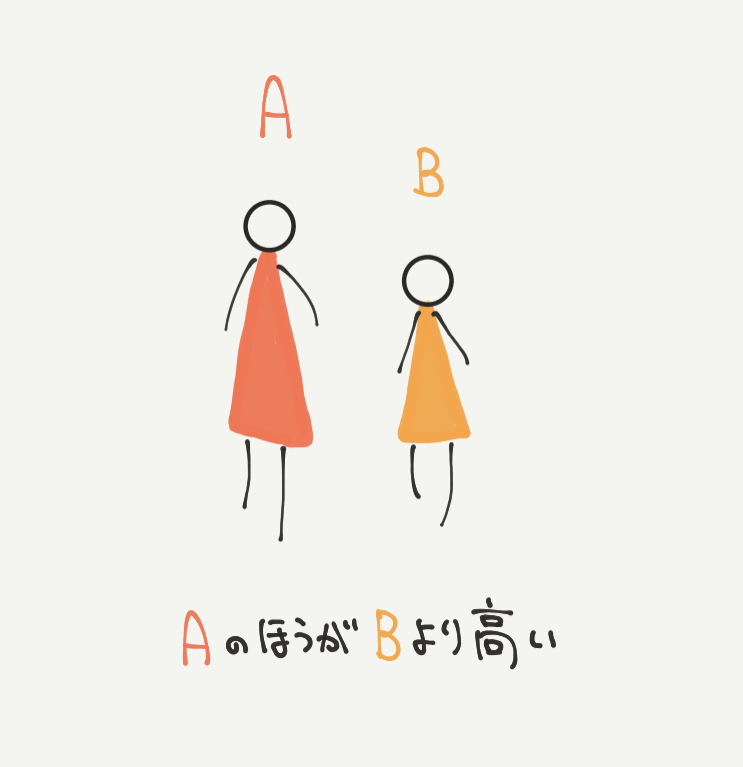
たとえばこちらの図ではAの方がBよりも高いですよね。
これはAがBの高さを基準きじゅんに考えているから高いと言えますし、BはAの高さを基準きじゅんに比べているので低いと言えます。

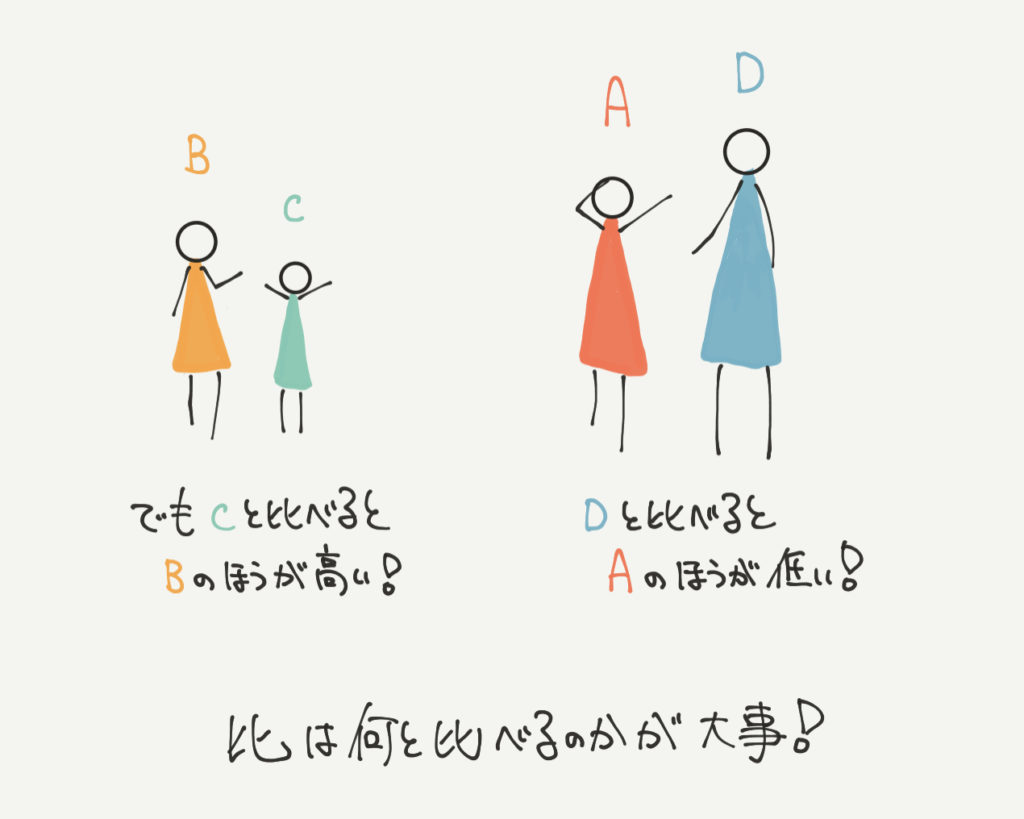
ところがBはCを基準きじゅんに考えると背が高くなりますし、AはDを基準きじゅんに考えると背が低くなります。
このように比の問題では「何を基準きじゅんに比べるのか」に注意しておくようにしましょう。

比の問題では「基準きじゅん」という言葉がたくさん使われるので覚えておくといいと思います！

④ベン図

「和と差に関する問題」では「ベン図」の考え方も出てきます。

ベン図ってなに？

ベン図は説明するより実際に書いてみた方がわかりやすいです！さっそくみてみましょう。

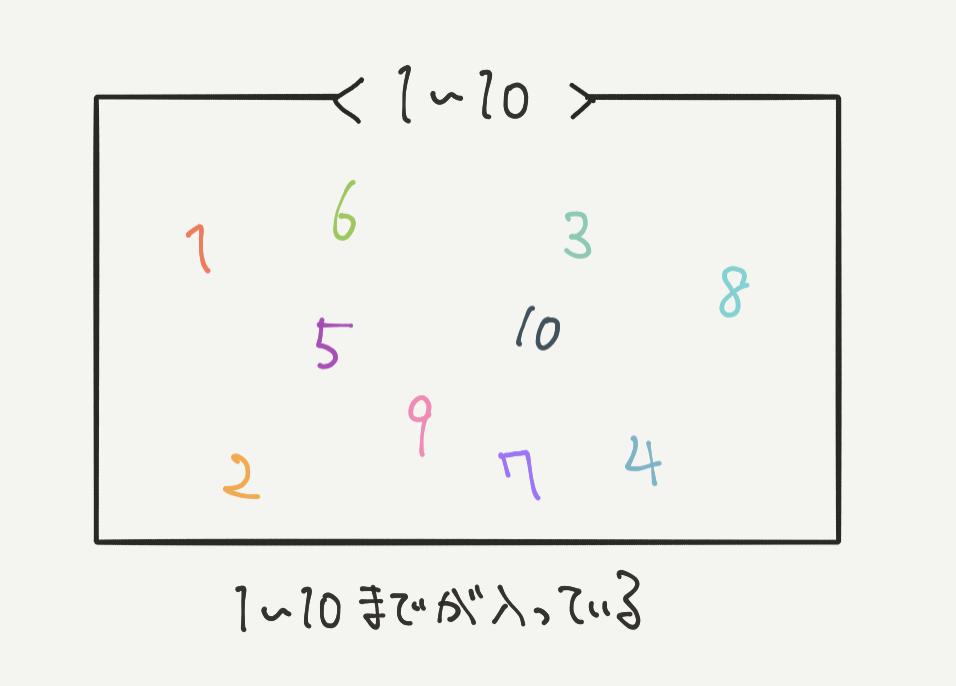
こういう図を「ベン図」と言います。
この図では1から10までの数をベン図を書いて表しています。
ここから追加でベン図に情報を書いていきましょう。

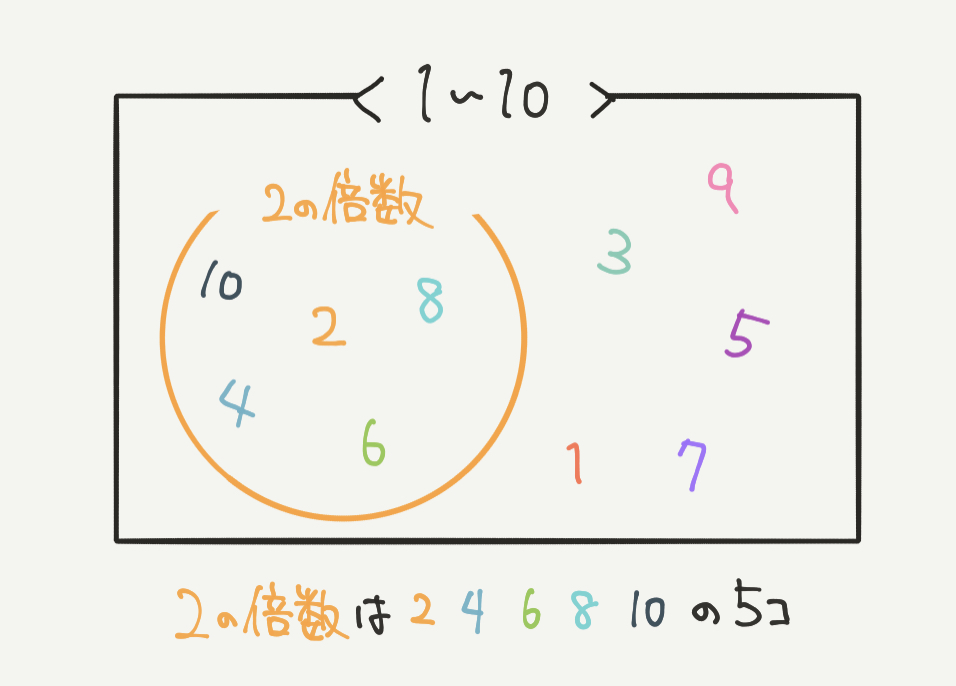
たとえばこちらの図では1から10までのベン図の中に、2の倍数を書いています。
1から10までのなかの2の倍数は2、4、6、8、10の5個になります。
1から10までの10個の数の中に2の倍数は、10÷2＝5個と求められます。

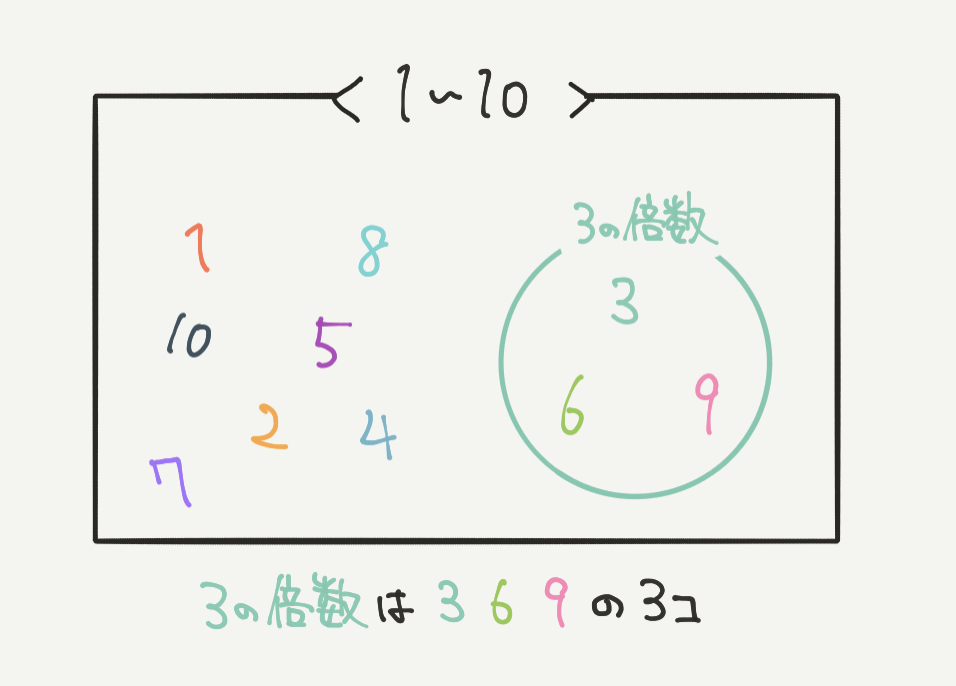
もう一つ、こちらの図では1から10までのベン図の中に、3の倍数を書いています。
1から10までのなかの3の倍数は3、6、9の3個になります。
1から10までの10個の数の中に3の倍数は、10÷3＝3個と求められます。

続いてこちらのベン図です！！

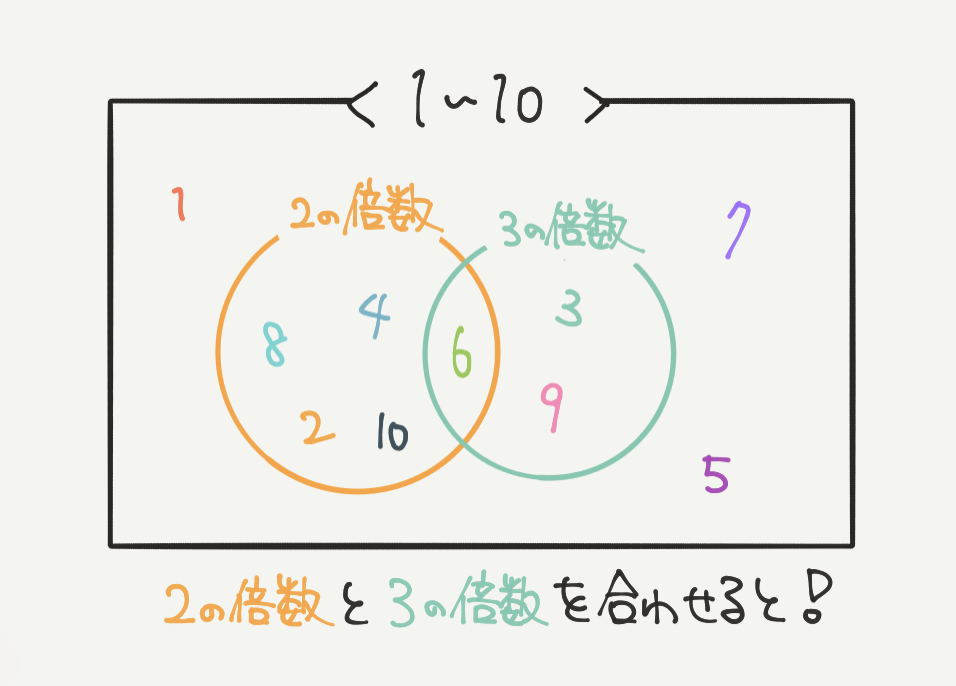
こちらのベン図では2の倍数を3の倍数を重ねて書いています。
すると数字の6がどちらの倍数にも含ふくまれていることがわかります。
まとめるとこのようにベン図は考えるようにしましょう・・・！！

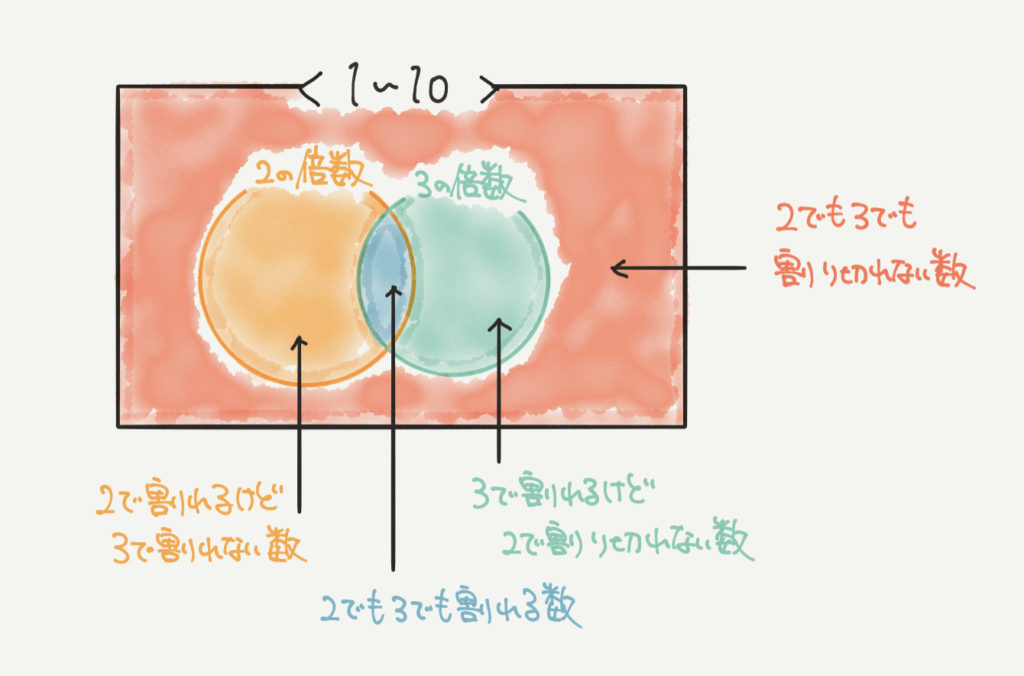
これらを理解した上で、ベン図の問題を解いてもらえるととてもわかりやすくなると思います！！

⑤仕事量の仮定

最後に仕事算についてのポイントもご説明します！！

仮定というのは「もし○○が□□だったら〜」と考えて問題を楽に解く考え方のことです。

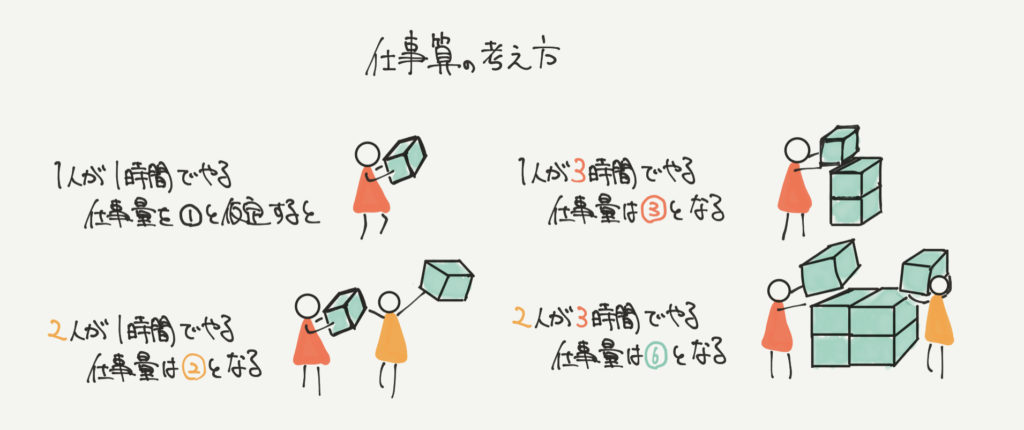
たとえば仕事算では「1人が1時間でやる仕事量を①と仮定する」とカンタンに問題を解けることが多いです。

この図では「1人が1時間でやる仕事量を①と仮定する」と、
「1人が3時間でやる仕事量を③」「2人が1時間でやる仕事を②」「2人が3時間でやる仕事を⑥」と表すことができます。

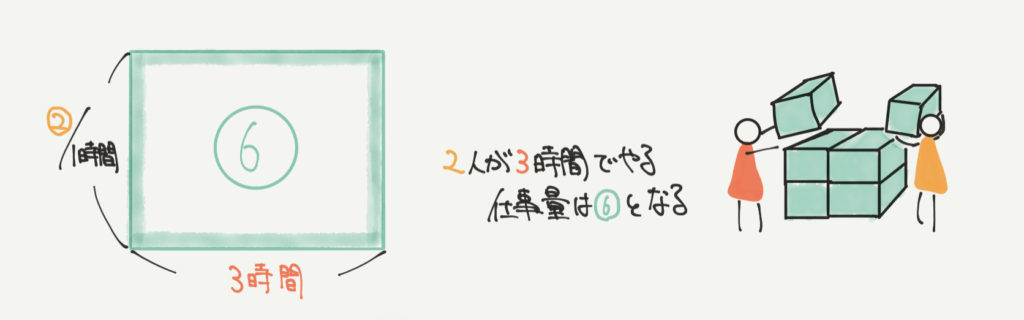
このように、仕事算の問題では、1人が1時間かけて行う仕事を①とおくといいと思います！

和と差に関する問題を得意にする5つのポイントのまとめ

和と差に関する問題の5つの重要なポイント（復習）

• 線分図と面積図の書き方
• 図の書き分け（面積図と線分図のどっちを書くか？）
• 比の考え方
• ベン図について
• 仕事量の仮定

さて、いかがでしたでしょうか。

「和と差に関する問題」ですが以上の5つの点を勉強してから問題に挑戦ちょうせんすれば今までよりもグッと正解が取れると思います。

とくにこの記事では「和と差に関する問題」だけではなく、「さんすうがく」の問題全部に言える大事なポイントがたくさん説明されているので、しっかり理解した上で問題を解くようにしてみてください！！

具体的な問題やその解説についても問題の記事で詳くわしく説明しています。
ぜひチャレンジしていきましょう〜！

和と差に関する問題はこちらから！