【中学受験攻略】三角形が作れないときってどういうとき？三角形を作る場合の数の問題にチャレンジ！

はじめに

今日は「 場合の数 」の問題の11問目です！
今回は三角形の秘密について勉強していきましょう。
前の問題を解きたい受験生は下の記事をクリックしてみてください！

三角形を作るときの条件！

中学受験の算数では三角形の成立条件を知らないと解けない問題があります。それが今回の問題です！
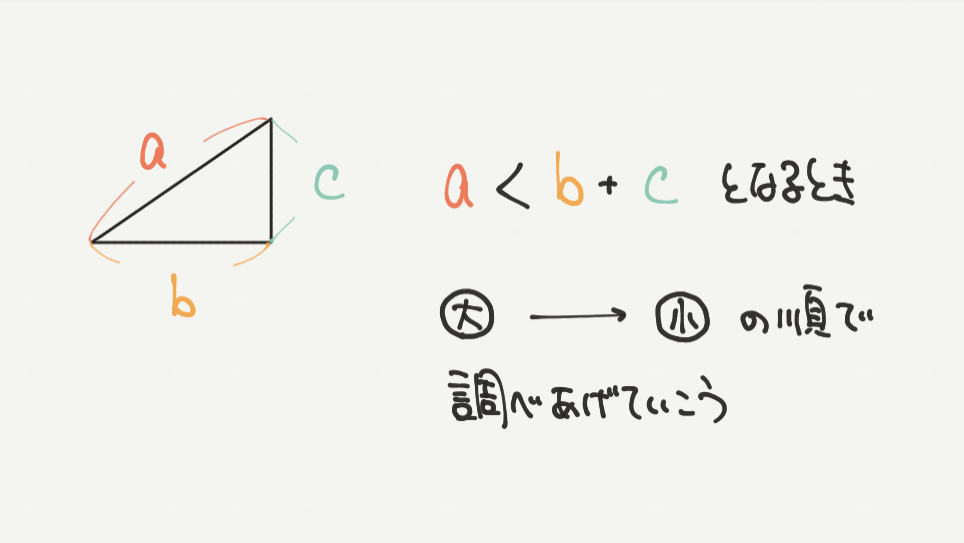
三角形が作れるときの条件は、三角形の1辺の長さがほかの２辺の長さの和よりも小さいことです。

たとえば、
a、b、cの三角形の辺ですとa＜b＋cとなる必要があります。

私たちがよく書く二等辺三角形とか正三角形はこの条件に当てはまっています。

反対に、
d、e、fの三角形ではd＞e＋fとなっています。

すると、上の図を見てみて下さい。
三角形が作れないことがお分かりいただけるでしょうか？

この三角形の成立条件を考えておかないとケアレスミスにつながるので、必ず気をつけて数えましょう！！

「 場合の数 」の問題に挑戦ちょうせん！

長さが3cm、5cm、7cm、9cm、11cmの棒ぼうが1本ずつあります。
このうち3本の棒ぼうを辺として三角形を作ると、全部で何通りの三角形ができますか。

解答

この記事を書いている人はこんな人

解説を読んで「 場合の数 」を攻略こうりゃくしよう！

STEP1：数えわすれがないように調べるときのルールを決めよう

今回の問題はいかに数えわすれずに調べることができるのかが大事でした。
場合の数では調べ上げるときのルールを決めましょう。
今回は（大、中、小）のルールにしたがって数を数え上げていきましょう！

STEP2：数の大きい数から調べよう（小さい方から調べてもOK！）

a＝7のとき
b＝5、c＝3しか組み合わせがありません。

a＝9のとき
b＝7か5、c＝5か3の組み合わせがあるので数えていきましょう。

a＝11のときは少し大変です。
b＝9か7か5、c＝7か5か3の組み合わせがありますね！

これらを数え上げていくと10通りとなります。

辺を組み合わせて作る三角形が何通りあるのか求める問題のまとめ

「 場合の数 」の問題で大事なポイント

三角形の成立条件
・三角形を作るためには辺の長さを考えないといけない
・長い辺の長さ＜他2つの辺の長さの和
調べ上げるときのポイント
・数えわすれがないように調べよう

以上で今日の問題は終わりです！
最後まで読んでくれてありがとうございました！！
次の問題で会いましょう！！！

その他の単元の問題の復習はこちらから！