目次
はじめに
みなさんこんにちは。「さんすうがく」の赤い小人です。
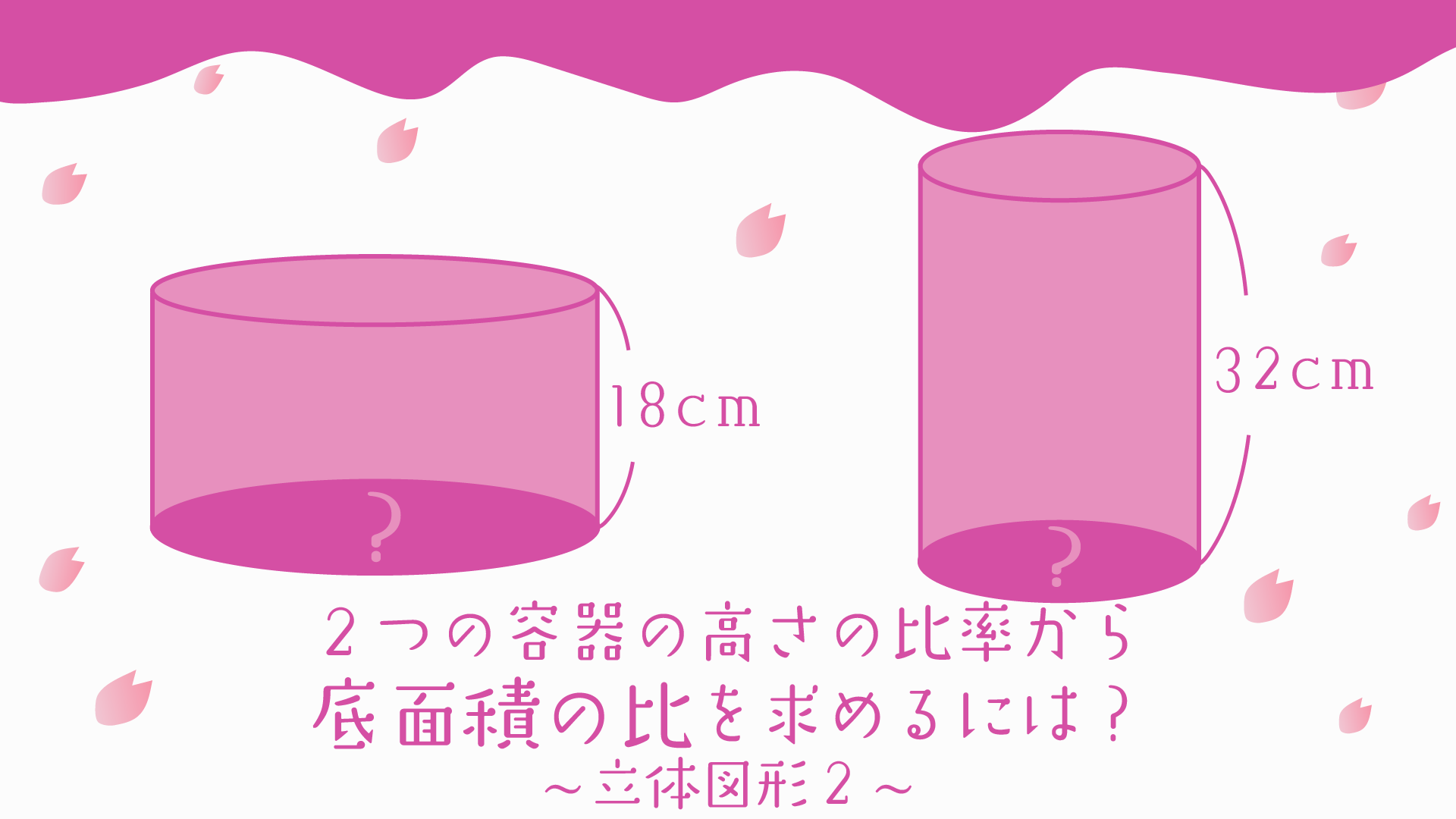
本日はニつの容器の高さの比率から底面積の比を求める問題について解説していきます！！
いつも通り、「立体図形」の問題を解くためのポイントを先に教えてください！！
まず問題から解きたいよ！っていう受験生の方はさっそく問題から解いてみてください！
面積が同じとき図形のたての比と横の比は反対になる
まずは今までの復習からしていきましょう！
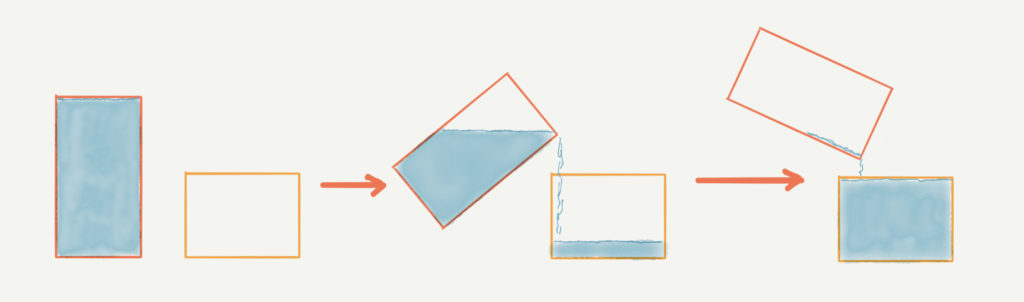
ここに赤い四角形と黄色い四角形があります。
赤の四角形に水が入っていて、それが全部黄色の四角形に移動しているので、2つの図形の面積が同じであることがわかります！
このときたての比と横の比は反対になる関係がありました。
たての比と横の比が反対になるのは、逆比の復習だね！
プチ復習：逆比ってなんだっけ？
赤い四角形と黄色い四角形の面積が同じのとき、たての比と横の長さの比は反対になります。
たとえば、面積が12の四角形があったとします！
このとき、たての比は6:3=2:1になります。
すると横の比はたての長さの比と反対になるので、横の長さの比は1:2となります。
これが逆比の復習でした！
今回に問題ではこの逆比を使いながら問題を解いてみましょう〜！
問題に挑戦！
深さがどちらも35cmの円柱型の容器A、Bに同じ量の水が入っています。水の深さは、Aが18cm、Bが32cmです。A、Bの容器の底面の半径の比を求めなさい。
解答は次のページから！
Amazonで好評発売中
この記事が役に立ったら、問題集にもチャレンジしてみよう！
中学受験に全敗した僕が、早稲田に合格するまでに見つけた勉強法を全60問に凝縮しました。線分図・面積図・仮定の考え方を、本番レベルの問題で実践できます！
Amazonで「下克上算数ドリル」を見る →
※ Kindle版なのでタブレットやスマホですぐ読めます
noteで受験のリアルを発信中
サイトでは書けない受験の本音、noteで話しています
受験生の不安とどう向き合うか、親はどこまでサポートすべきか。12校全敗からの経験を、もっと深くお伝えしています。フォローしてくれたらうれしいです！
noteをフォローする →
※ 無料で読める記事もたくさんあります
