【SPI試験徹底対策】非言語の代金精算を徹底攻略！得した分を＋に損した分を−にして練習しよう！！（全４問）

2023年12月7日

はじめに

わかみや先生

みなさん、こんにちは！「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として
本日もSPIに関する情報やコツをお届けしていきたいと思います！

今回は「代金精算」に関する問題です！

代金精算の問題は中学入試や高校入試では滅多に出題されない問題と言っていいでしょう。
お金のやり取りの問題で、他の単元よりも身近に感じてしまいますね笑

さて、このような状況でお互いが損しないように
お金を払うためにはどのようなことに注意して解いていけばいいのでしょうか？？

［138］問題に挑戦！

［138］ X,Y,Zの3人で食事した。食事代は12000円だったが、その場でXが1000円、Yが2000円を支払った。その後、喫茶店に入り、ここではコーヒー代900円をZがまとめて支払った。3人が同額ずつ負担するためには、YとZはXにいくらずつ支払えばよいか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

YがXに2300円
ZがXに3400円

［138］解説を見てみよう！

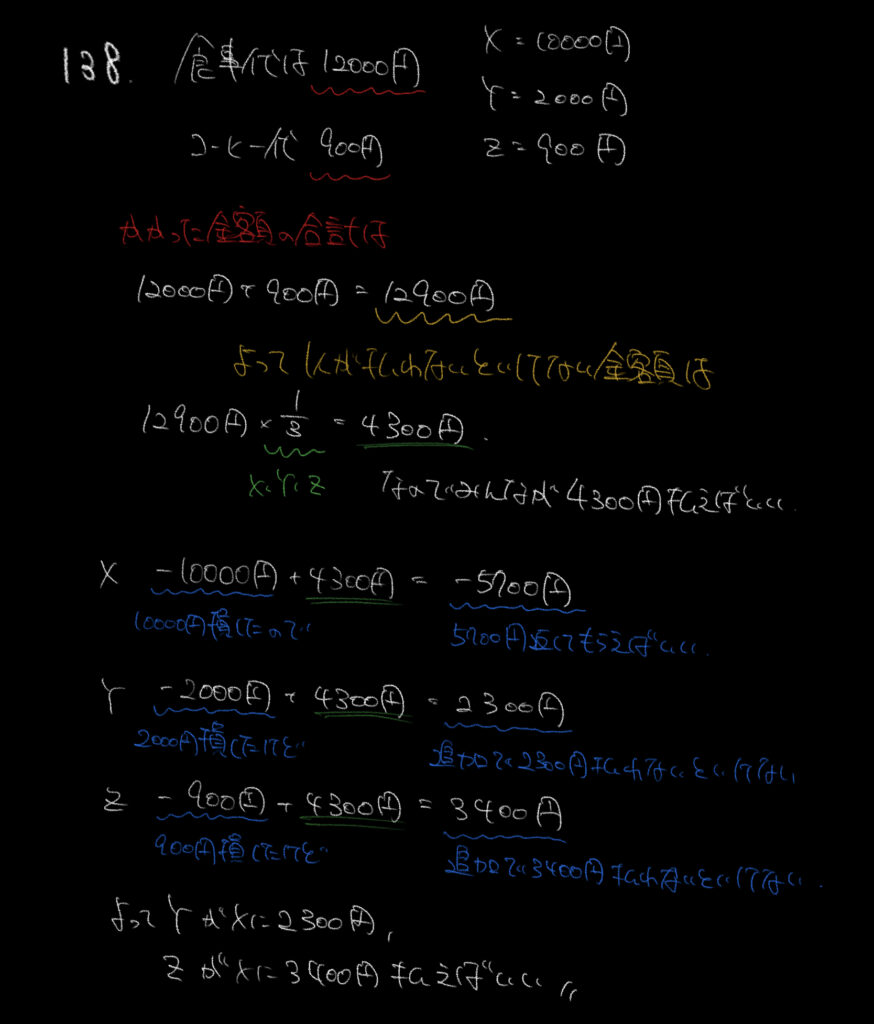
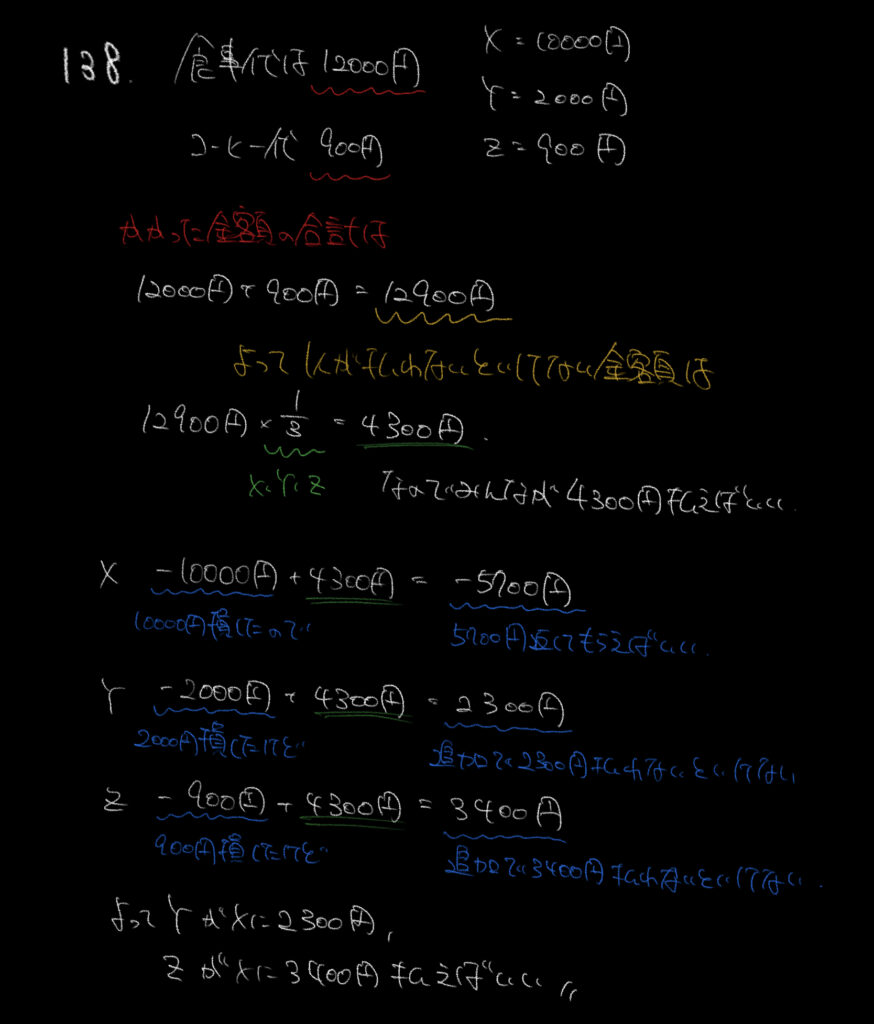
こういう場合は、まず3人が払った合計金額を求めて、1人が払わないといけない金額を求めましょう。
3人がトータルで支払った金額は食事代12000円とコーヒー代900円の合計12900円です。
3人でそれだけ支払ったので1人が支払わないといけない金額は、

12900円÷３人＝4300円/人と求まります。

ここでそれぞれの損得をプラス、マイナスを使って表しましょう。

Xは−10000円＋4300円＝−5700円となり、5700円返してもらいたい。
Yは−2000円＋4300円＝2300円となり、2300円追加で支払う。
Zも同様に−900円＋4300円＝3400円となり、3400円支払う。

これらをまとめると、XにYが2300円、Zが3400円支払えば貸し借りをなくすことができます。

ちなみに、もうお分かりかと思いますが
このような代金精算の問題はプラスとマイナスの合計が必ず０になります。
今回だと、−5700円＋2300円＋3400円＝０になります。

代金精算の考え方

お金の問題は損した金額をマイナス、得した金額をプラスで表しましょう。

そして貸し借りがないようにするには、
プラスの人（得している人）がマイナスの人（損している人）にお金を払えばいいということです。

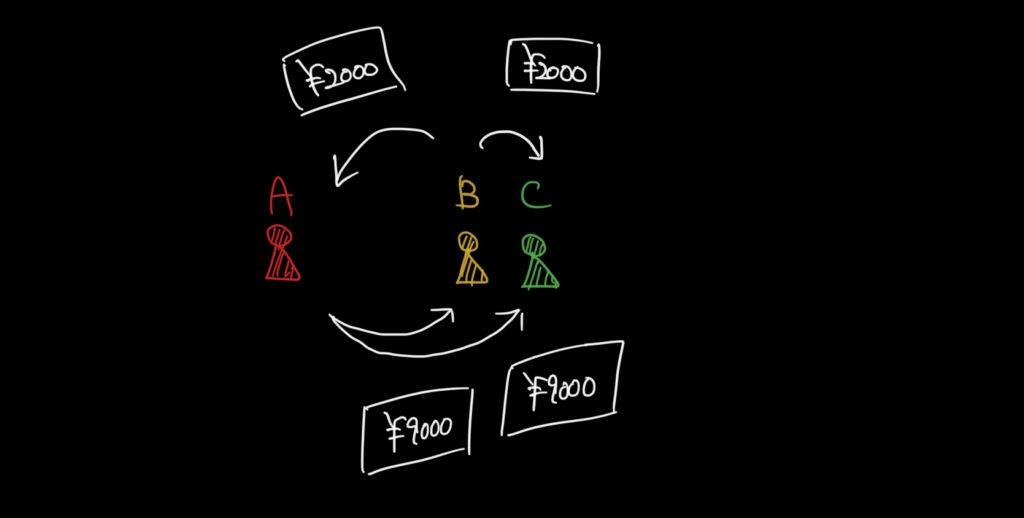
例えば、Aさんは9000円分ずつBとCにお金を貸していて、
Bさんも2000円ずつAとCに貸しています。
これを貸し借りがなくなるようにするには誰が誰にいくら払えばいいのでしょうか。

それぞれの貸し借りを表でまとめるとこのように書くことができます。

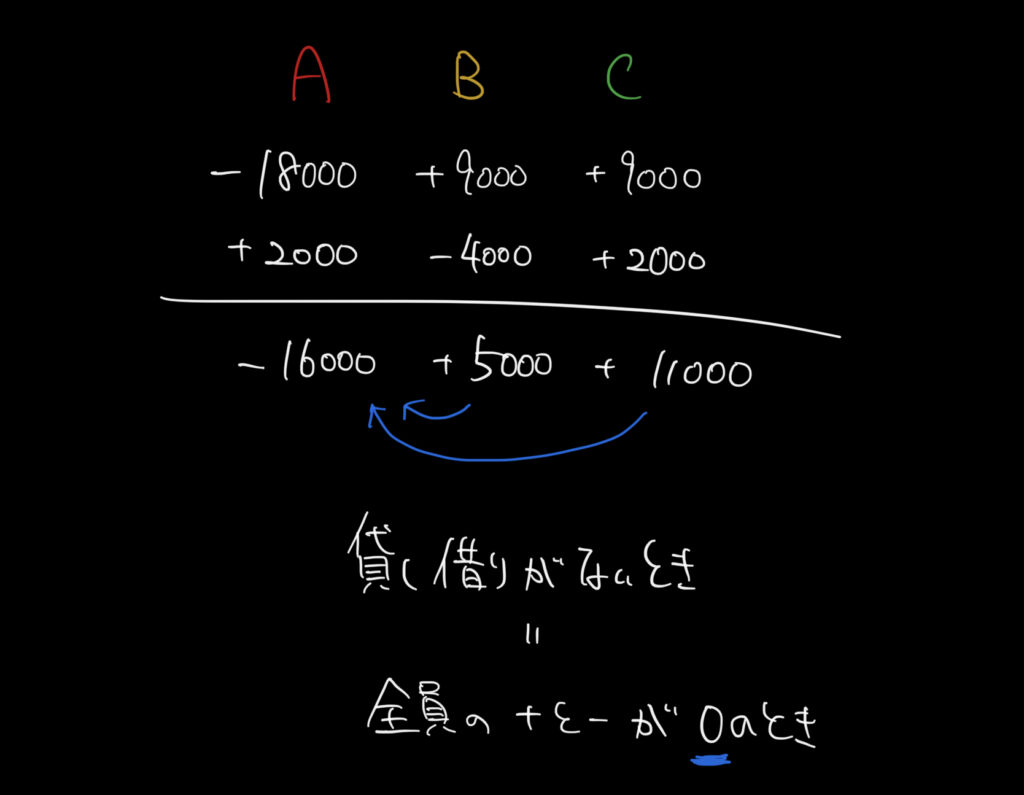
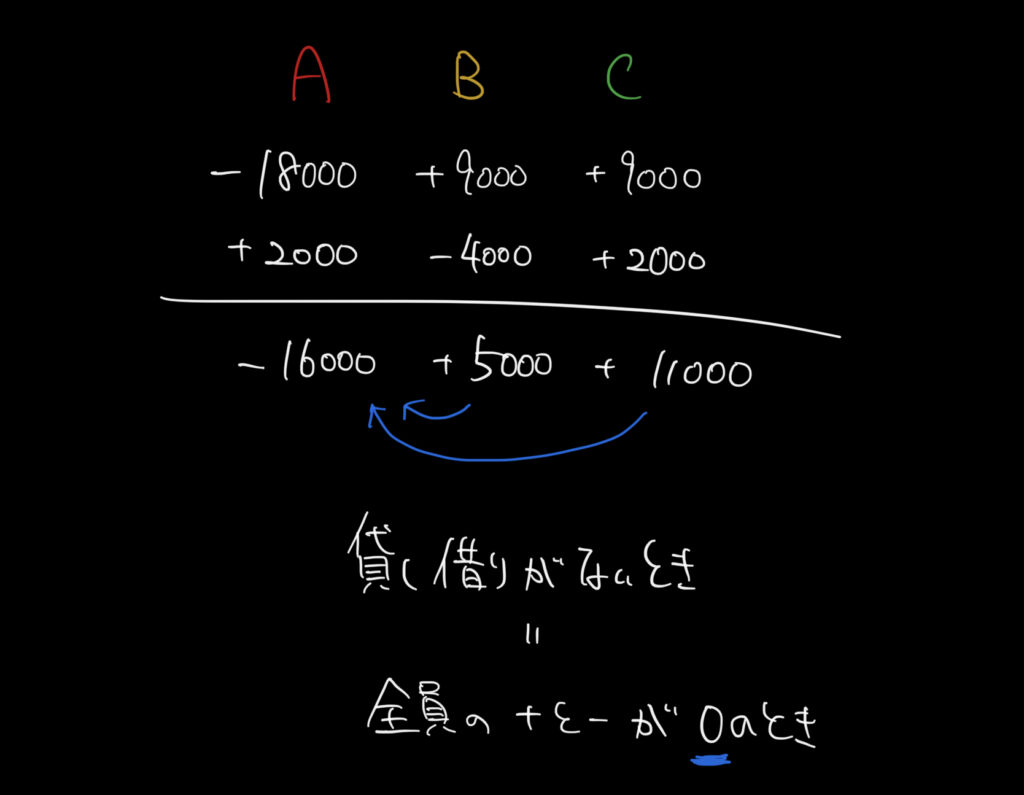
はじめの段はAくんがBとCに9000円ずつお金を貸しているとき、
Aは2人分の18000円を支払っていて、BとCは9000円ずつ得したことになります。

同じように書き込んでいくと、２段目ではBが2人分の4000円を損していて、AとCが2000円ずつ得をしている。

これらをまとめるとAは16000円損していて、
BとCがそれぞれ5000円、11000円ずつ得していることがわかります。

なので貸し借りのないようにするには
BがAに5000円、CがAに11000円を渡せばいいことがわかります。

ここまでが代金精算の考えです。
得している部分をプラス、損している部分をマイナスと書くことが重要な理由はわかったでしょうか？

［139］問題に挑戦！

［139］SとTの2人が、半分ずつお金を出し合って、レストランで友人の送別会を開くことになった。店から出るときに、SはTから10000円を預かって支払いに向かったが、支払いは13000円だったので、Sが3000円を上乗せして支払いを済ませた。この後で、TはSにもともと6000円の借金があったことがわかった。
①精算のとき、SがTに「あなたから10000円預かっていたが、もともと6000円貸していたので、4000円をもらったことになる。支払いでは私が3000円を出したので、差額の1000円を折半して500円をあなたに払えば精算できるね」と言った。このように精算すると、Sはいくら得をするか、または損するか？
②本当はどのように精算をすれば、貸し借りがなくなるか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

①Sは3000円損する
②TがSに2500円渡す

［139］解説を見てみよう！

①かなりめんどくさい問題だったと思います。
実際私も頭の中でやるとごちゃごちゃになってしまいそうでした。
SPI本番でもこのパニックに陥って点数が取れなかったという友人を見てきました。

時間がかかってしまうかもしれませんが、やっぱり一度図をかきましょう。
これが何よりも正確な、正解への近道だと思います。

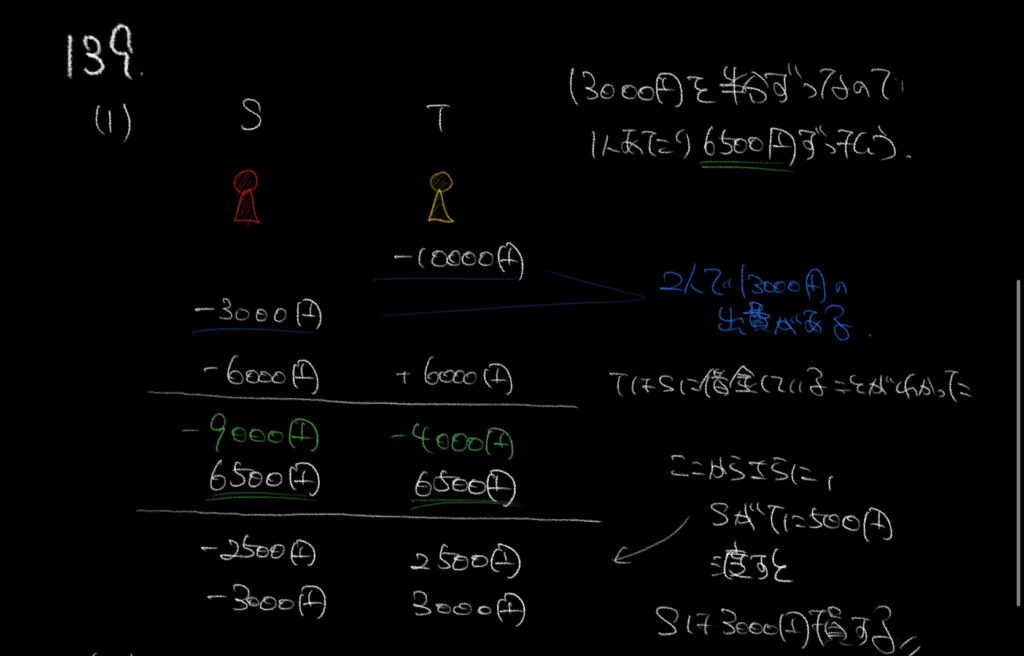
まず初めにTが10000円、Sが3000円支払いました。
ここでそれぞれ−10000円、−3000円と書き込むことができます。

ここから、TがSに借金していることがわかるので、Tは6000円得していて、
Sは6000円貸しているので−6000円となります。

借金しているとき、TとSのプラス、マイナスを反対にして考えないようにしましょう。

また、2人は合わせて13000円支払ったので1人あたりが払う金額は6500円になります。
よってSが2500円損して、Tが2500円得したことがわかります。

ここから①の情報を足していきましょう。
言っていることが支離滅裂でよくわかりませんが、ポイントは最後の一言。
SがTに500円支払うというところがポイントです。ここさえわかればあとは無視で構いません。

SがTに払うので、Sはさらに500円損し、Tは500円得します。
よって、最終的にSは3000円損をして、Tは3000円得をします。

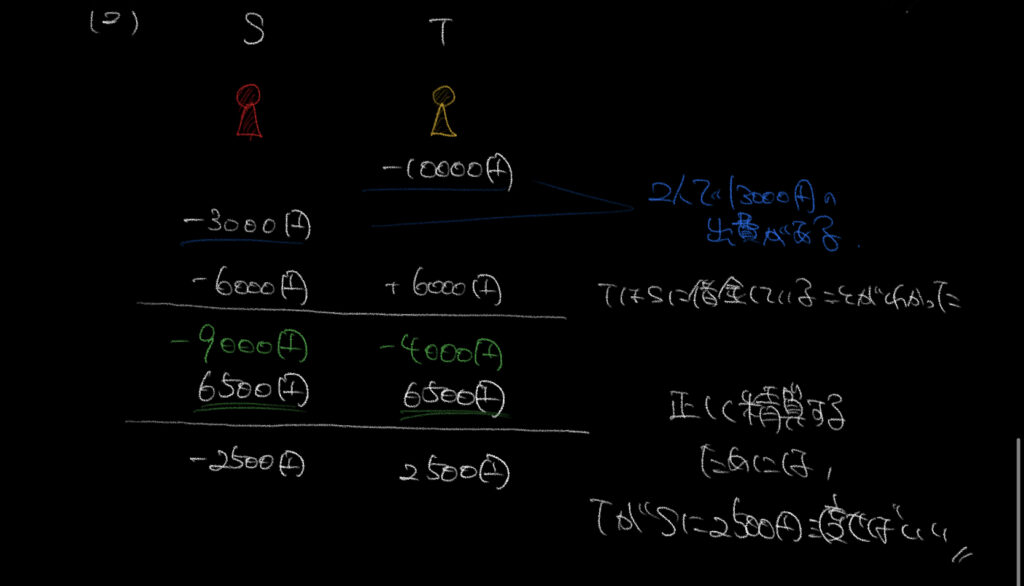
②①でほとんど求めているので、問題ないと思います。
先ほどの表をまとめるとSが2500円損して、Tが2500円得しているので、
TがSに2500円支払えばいいことがわかります。

［140］問題に挑戦！

［140］ XがYから5000円預かって、Yのネクタイを１本買うことになった。Xは3500円の青のネクタイ１本と3000円のグレーのネクタイ１本を買い、Yが選ばなかった方を自分のものにすることにした。もともとYはXから4000円の借りがあった。Yが青のネクタイを選んだとき、これまでの貸し借りもなくなるように精算するには、どのようにすればよいか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

YがXに2500円払えばいい

［140］解説を見てみよう！

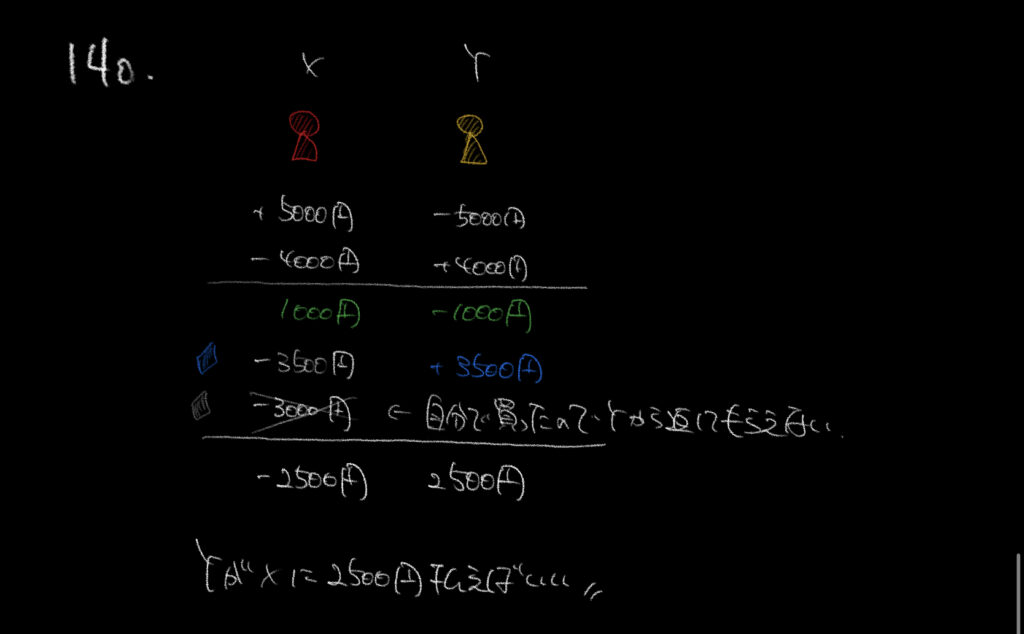
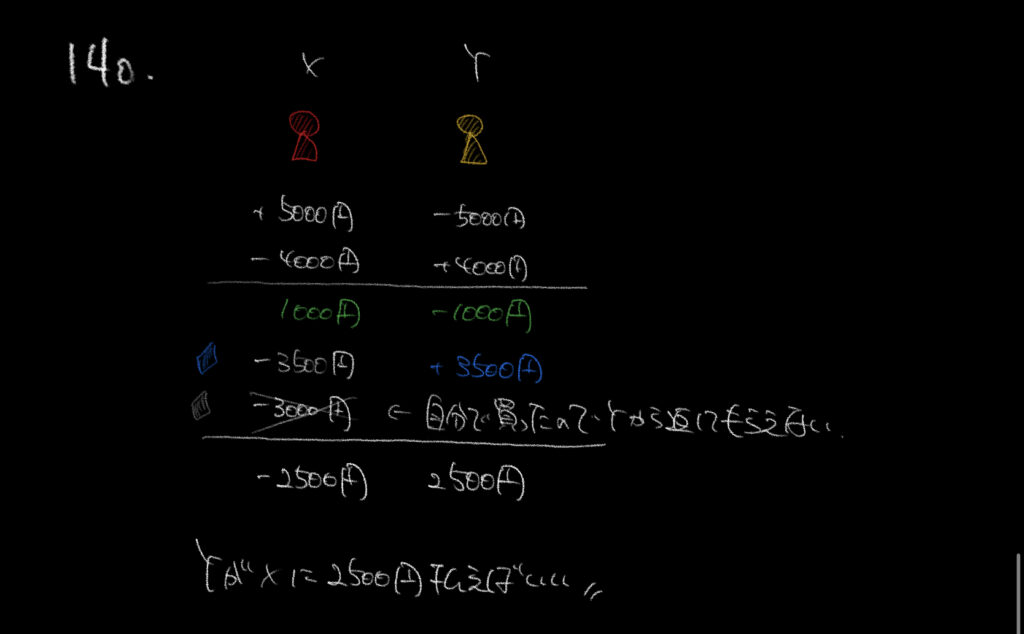
Yが選ばなかった方を自分のものにすることにする、というのがこの問題のポイントでした。
今回Yは青を選んだので、選ばれなかったグレーのネクタイ3000円分は
Xが一人で買い物をしたということになります。

ここに気をつけて、表を書いていきましょう。

XがYから5000円預かっているので、Xは5000円得をして、Y5000円損しています。
さらにお金のやりとりが4000円分あるので、トータルでXは1000円分得をして、
Yは1000円分損していることが分かります。

追加でYが3500円分の青いネクタイを選んだので、一時的にXが3500円分損し、Yが3500円得します。
これらを合わせると、Xが−2500円、Yが＋2500円となり、YがXに2500円支払えばいいことが分かります。

［141］問題に挑戦！

［141］ L,M,Nの3人が同額ずつお金を出し合って友人にプレゼントをすることにした。3人には、もともと次のような貸し借りがあった。LはMに1500円貸していた。NはMに2000円を貸していた。プレゼントはMが買いに行くことになっていたが、病気で行けなかったため、NがMから10000円を預かって買いに行った。
①Nが9000円でプレゼントを買ってお釣りは自分でもらった場合、後で全員の貸し借りがなくなるように精算するためには、Nはいくら支払えばよいか。
②Nがいくらかを上乗せして10000円以上のプレゼントを買ったところ、精算時にはLがMに2000円、Nに1000円を支払うことになった。この場合、プレゼントの値段はいくらだったか。

SPI＆テストセンター超実践問題集/ナツメ社

答えを見るにはここをクリック！

①Nは2000円払えばいい
②15時間

［141］解説を見てみよう！

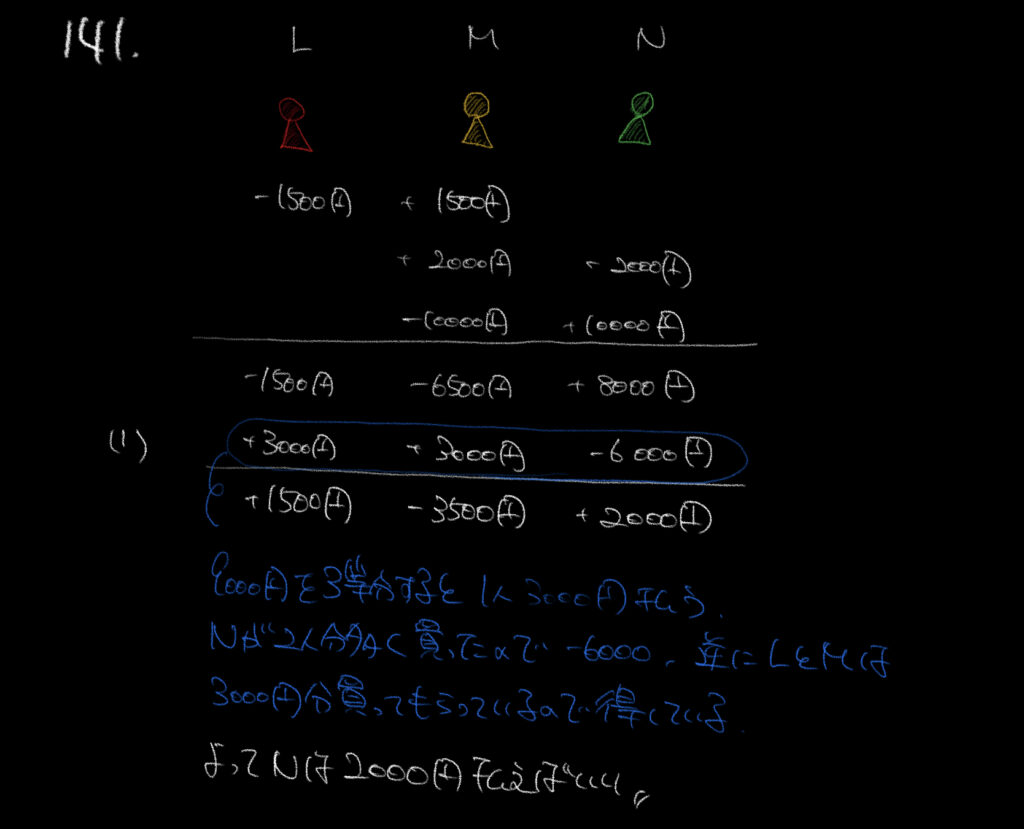
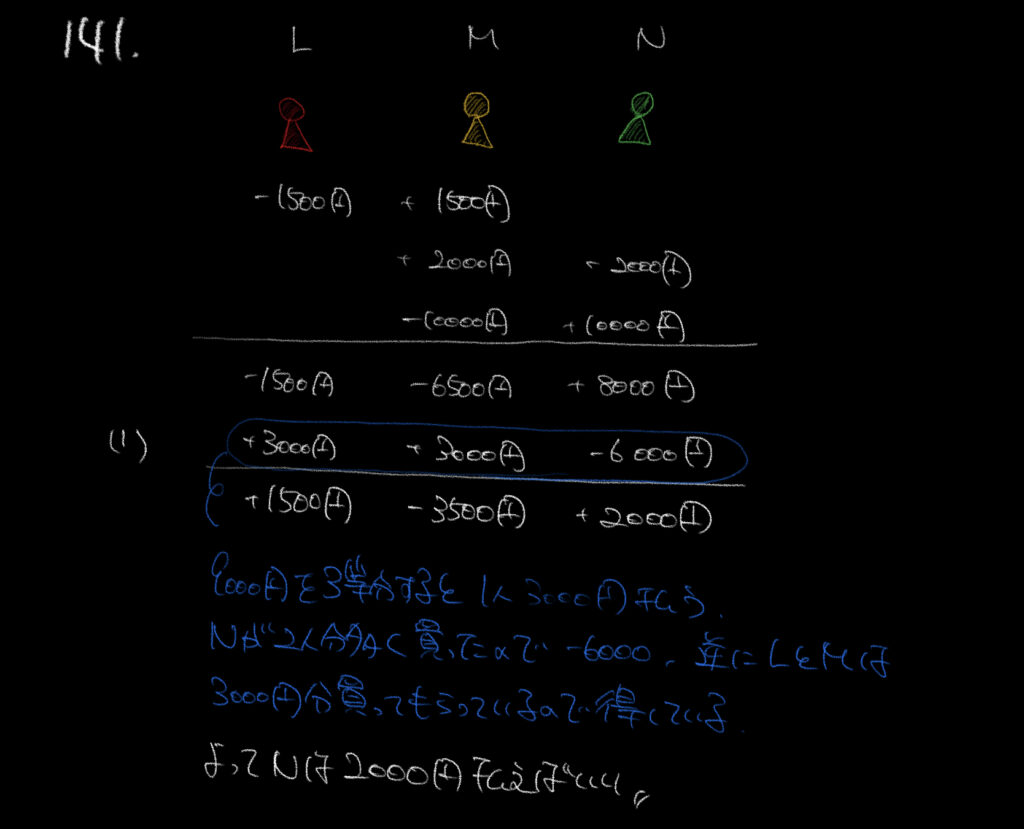
情報がたくさん出てきましたね。
一旦時間のことは気にせずに書き出してみましょう！

LはMに1500円貸していた→L＝−1500円、M＝＋1500円
NはMに2000円を貸していた→N＝−2000円、M＝＋2000円
NがMから10000円を預かった→N＝＋10000円、M＝−10000円
と、これらのことが問題文からわかります。

ここからが本題です！！

①9000円のものを3人で均等に支払うので、全員が3000円ずつ支払わなくてはいけません。
しかしNが9000円払ったので、LとMは3000円ずつ得をして、Nは6000円分損していることになります。

これをはじめの表に書き入れると、
L＝＋1500円
M＝−3500円
N＝＋2000円
となり、Lが1500円をMに、Nが2000円をMに支払えばいいことが分かります。

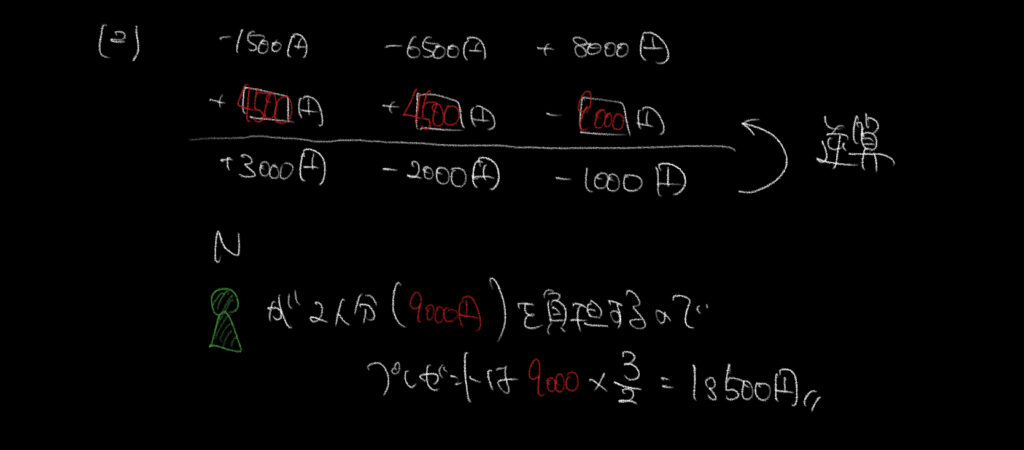
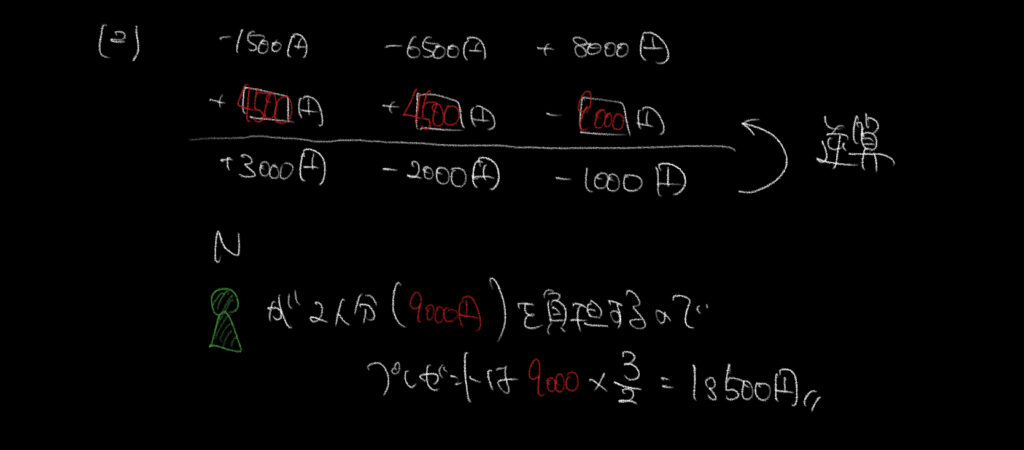
②①と反対に考えましょう。
いくらかわからないものを□にして考えてみましょう。
先ほどと同じように、NはLとMの2人分を負担していることを忘れないようにしましょう。

問題文にLがMに2000円、Nに1000円を支払うことになったと書いてあるので、
ここから3人の最終的な金額が

L＝＋3000円
M＝−2000円
N＝−1000円
となり、Nが負担した2人分の金額が9000円と分かります。
（2人分で9000円の金額なので勘違いしないようにしましょう！）

よってプレゼントは3人分の合計金額なので13500円と分かります。

まとめ

以上が「代金精算」の問題でした！いかがでしたでしょうか？

代金精算は一見複雑でめんどくさく思ってしまうかもしれませんが、
しっかりと表を書いてプラス、マイナスを理解すればそこまで苦戦するものはありません。

むしろ問題文が長い方が有利な場合もあります。

表を書くのに時間がかかるかもしれませんが、
それでも１問１問正確に解き進めていくことが内定への近道だと私は思います。

頑張っていきましょう！！

参考になったらぜひシェアお願いします！

URLをコピーしました！

URLをコピーしました！

【SPI試験徹底対策】非言語の代金精算を徹底攻略！得した分を＋に損した分を−にして練習しよう！！（全４問）

はじめに

［138］問題に挑戦！

［138］解説を見てみよう！

代金精算の考え方

［139］問題に挑戦！

［139］解説を見てみよう！

［140］問題に挑戦！

［140］解説を見てみよう！

［141］問題に挑戦！

［141］解説を見てみよう！

まとめ

関連記事

解き方から問題に挑戦