はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います!
今回は「仕事算」に関する問題です!
仕事算のコツはタイトルにもあるとおり、仕事量を仮定することです。
この記事では仕事算を「面積図」と「仮定」を使って解いています。
メモを読みながら一緒に解いていきましょう!


この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
[134]問題に挑戦!
答えを見るにはここをクリック!
①22時間30分
②15時間
[134]解説を見てみよう!


今回仕事量もわかっていなければ、2人のそれぞれの仕事の割合もわかっていません。
困ったものです。
とりあえず、2人の仕事量を仮定して面積図をかいてみましょう。
面積図を書くことで同じところを見つけやすくします。
この問題における同じものとは、仕事量のことです。
2人で9時間やった量と、バラバラで終わらせた量と
どちらも同じ仕事量をこなしたことが問題文からわかると思います。
この情報を踏まえ面積図を書いていくと、
9X+9Y=3X+18Y、であることがわかります。
これを変形すると、
6X=9Yとなり、
X:Y=3:2、と2人の仕事量を表すことができます。
Xの仕事量が③/時、Yの仕事量を②/時と仮定すると全体の仕事量を㊺と表せます。
①全体の仕事量㊺を②/時で行うので、全部でかかる時間は
22.5時間となり、22時間30分となります。
②全体の仕事量㊺を③/時で行うので、全部でかかる時間は15時間となります。


SPI対策:仕事算の考え方
この単元は中学受験の内容でもある「仕事算」です。
ここで仕事算について簡単におさらいしておきましょう。
仕事算は基本的にわからない量がいくつかあります。
例えば、全体の仕事量であったり、仕事をする人の量などです。
わからない数が多いと混乱してしまうので、1人が1時間で作業する量を①と仮定することが基礎的な考えです。
今回のように、SPIの問題によっては2人の仕事量が違ってくる場合もあるので、
その際はそれぞれの仕事量を別々に仮定する必要があります。
(この問題では○のXと○のYと仮定しています。)
仮定するときの注意事項にあったように何を仮定するのか、で問題の正解率は大きく変わってきます。
これらのことに気をつけて問題を解いてみましょう。
[135]問題に挑戦!
答えを見るにはここをクリック!
①5/27
②4/27
[135]解説を見てみよう!


国と地方自治体が2:1と書いてあるので、総建設費を③と仮定します。
これを①と仮定しても解けなくはありませんが、
かなりめんどくさくなるので問題文から楽できるところはきちんと楽していきましょう!
③と仮定したうち、地方自治体の割合が①なので、A県・B県・C県の合計が①ということになります。
❶A県の割合は総建設費の4/27なので③×4/27=○の4/9となります。
残った2つの県は①から○の4/9を引いた○の5/9。
聞かれているのは総建設費に対する割合なので、5/27となります。


❷は❶の続きです。
A県の割合は、○の4/9と求めていたので、B県とC県について考えましょう。
B県の割合は地方自治体の1/9なので○の1/9となります。
決して総建設費の1/9としないように!!!
ここから、C県の建設費が○の5/9−○の1/9=○の4/9となります。
よってC県の費用は総建設費③の4/27となります。
[136]問題に挑戦!
答えを見るにはここをクリック!
①1時間15分
②3時間45分
[136]解説を見てみよう!
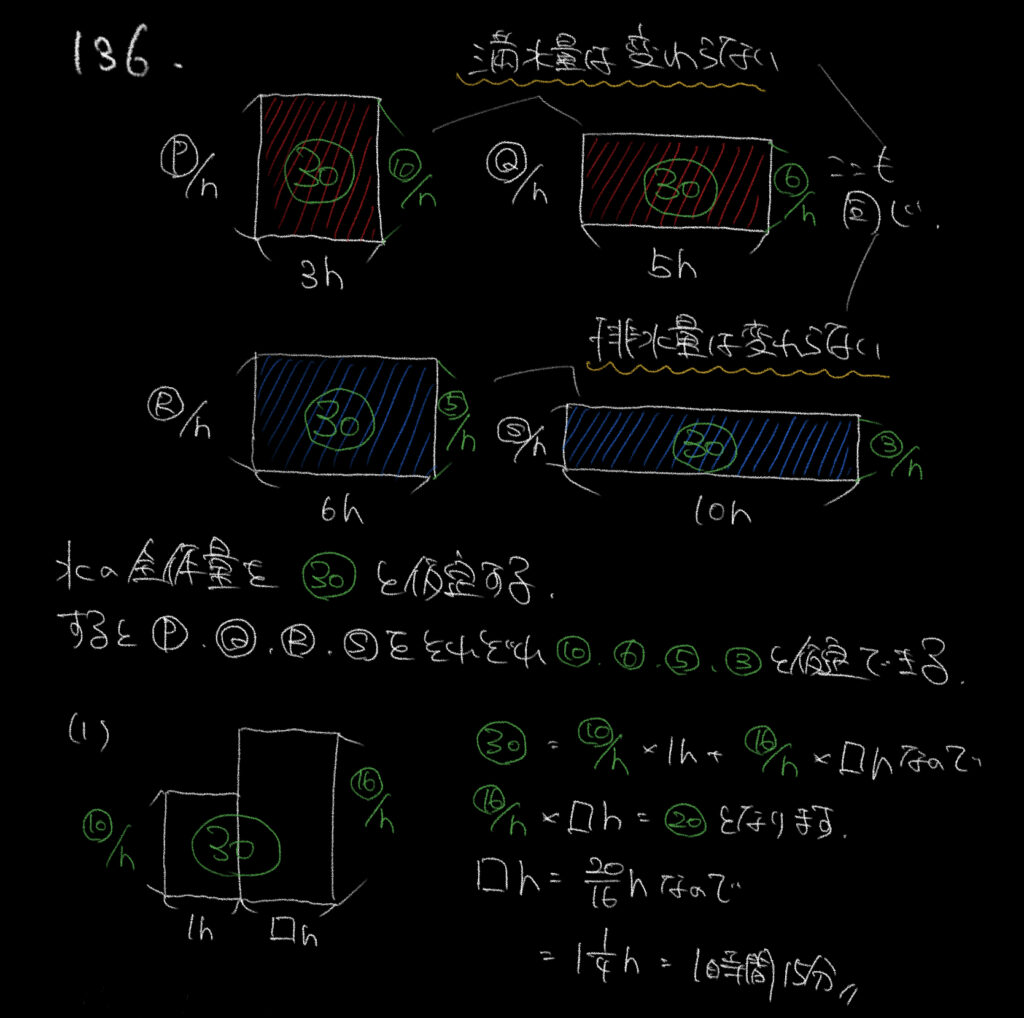

[134]にもあったようにわからない量がいくつかあって、
それぞれの仕事量が一定ではないのでそれぞれの仕事量をP、Q、R、Sと仮定します。
ここで少しニュートン算(水の出し入れの問題)の復習です。
SPI対策:ニュートン算の考え方
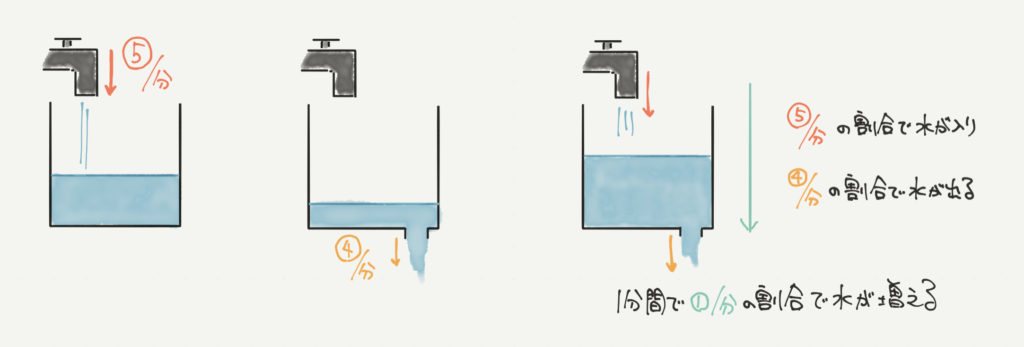

ニュートン算は水が入ったり出たりしてかなり複雑になる問題が多いです。
そのため基本的な考え方として入る量と出る量の2つを考えるのではなく、
トータルで入る(または出る)量を考えます。
例えば、毎分⑤ℓの割合で注水している管と、毎分④ℓの割合で排水する管があったとして、
10分後に器の中に入っている水の量を求めたいとします。
注水と排水を別々で考えると、
注水する割合:毎分⑤ℓ×10分=㊿ℓ
排水する割合:毎分④ℓ×10分=㊵ℓとなり、
容器に入っている量を㊿ℓ−㊵ℓ=⑩ℓと求めることができます。
しかしこれを注水と排水を合計して、結果的に器に入る量のみで考えると、
1分で⑤ℓの注水−④ℓの排水で毎分①ℓの水が入ることになります。
なので10分間で、毎分①ℓ×10分=⑩ℓと求めることができます。
このように考えてニュートン算を解いていきましょう。


今回の問題は出てきている数字が3、5、6、10なので最小公倍数の㉚と仮定して考えます。
すると、P、Q、R、Sそれぞれの注水、排水の割合を求めることができます。
P=㉚÷3時間=⑩/時の割合で注水する
Q=㉚÷5時間=⑥/時の割合で注水する
R=㉚÷6時間=⑤/時の割合で排水する
S=㉚÷10時間=③/時の割合で排水する
と、以上のような割合が仮定できます。
これを元に問題を解いていきましょう。
①空の水槽を㉚と仮定してPで1時間(⑩の量を)注水していたので
水槽には残り⑳入るということになります。
PとQは合わせて⑯割合で注水されるので、5/4時間で水槽はいっぱいになります。
5/4時間=1時間15分となります。
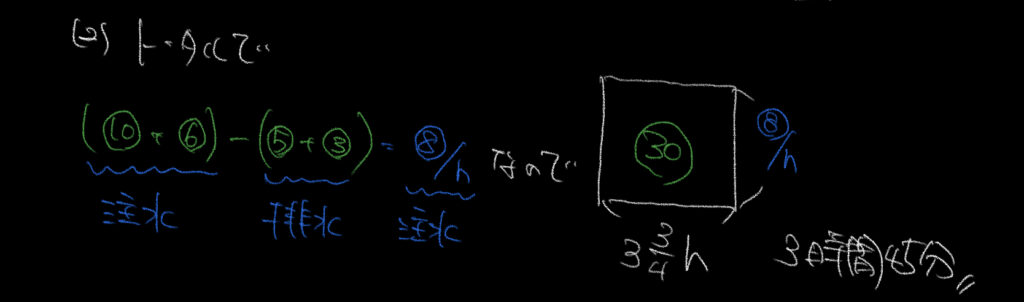

②トータルの入る(または出る)水の量を考えましょう。
解説にも書いてある通り、それぞれの注水排水の割合は以下の通りです。
P=⑩/時の割合で注水する
Q=⑥/時の割合で注水する
R=⑤/時の割合で排水する
S=③/時の割合で排水する
よって、P+Q−R−S=⑩+⑥−⑤−③=⑧/時で注水されます。
ここから㉚たまるのにかかる時間は、15/4時間=3時間45分となります。
[137]問題に挑戦!
答えを見るにはここをクリック!
①3/40
②1/2
[137]解説を見てみよう!


設定がかなり特殊な問題でした。
私も頭でやるとこんがらがってきそうだったので、お絵描きしてみました。
これなら少しは理解できそうな感じがしますよね。
それではやっていきましょう。
①金額全体の25%を払ったので全体の量を○の100と仮定すると、
頭金㉕を除いた、残りの量は○の75になります。
ここで利子について考えなければいけません。
問題によると、残った金額には10%の利子が上乗せされます。
よって実際に払わないといけない金額は○の75ではなく、
○の75×1.1(利子10%増)=○の82.5となります。
これを11等分した○の7.5が1回あたりに払う金額になります。
これは全体の7.5/100=3/40となり、答えが出せます。
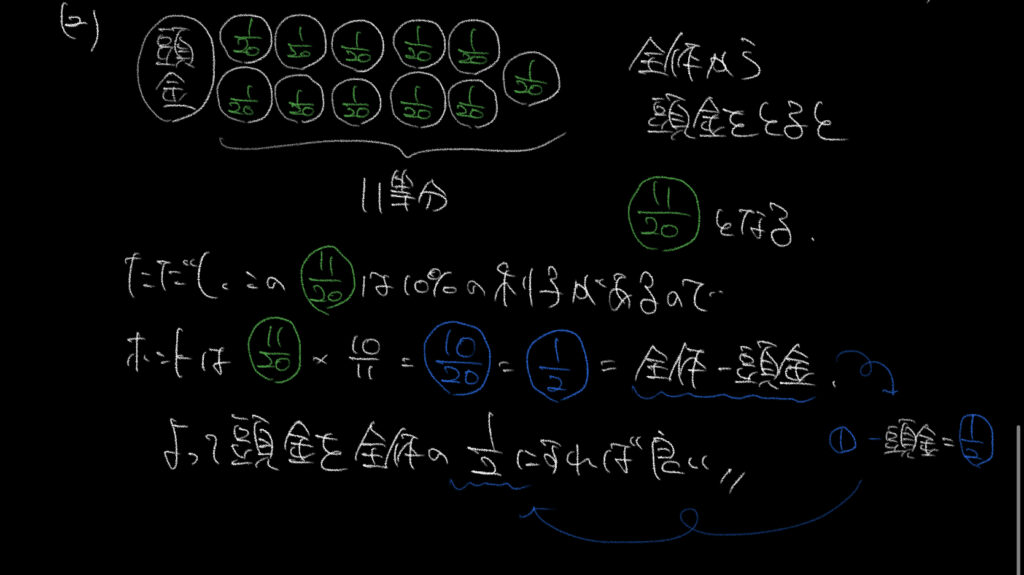

②①と反対の考え方で解いていきましょう。
1回あたりの量が○の1/20なので11回分で○の11/20となります。
しかしこれは10%の利子が上乗せされている金額なので、実際の金額は
○の11/20×10/11で○の10/20=○の1/2となります。
全体から頭金を除いた金額が○の1/2なので、
頭金は全体の1−1/2=1/2
50%と求めることができます。
まとめ
いかがでしたでしょうか。
一見難しく見えるSPIの問題でも中学受験の解法でも十分太刀打ちできます。
難しく感じているなら、もう少し簡単な問題で復習しておきましょう。
大事なのは仮定することでしたね。
仮定の考え方は今後もいろんなSPIの問題で出てきますのでしっかり復習しておきましょう。












