【SPI試験徹底対策】損益算は割合の復習！売買損益の仕組みを理解して面積図を書いて克服していこう！（全９問） 2023 12/05 就職活動 SPI 2023年12月5日 目次はじめに わかみや先生 みなさん、こんにちは！「さんすうがく」のわかみや先生です。大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います！ 今回は「売買損益」に焦点を置いた問題です！実はこの問題の攻略のポイントも「割合と比」になります。これまで２つの記事で「割合と比」に関する問題を解説してきました。詳しく知りたい方は先に下の記事をご覧ください！ あわせて読みたい 【SPI試験徹底対策】割合と比は中学受験のおさらい！記号を使った大学生向け攻略法をご紹介！（全10問） 【】 みなさん、こんにちは！「さんすうがく」のわかみや先生です。大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います！ … あわせて読みたい 【SPI試験徹底対策】割合と比を完全攻略！長文問題も楽々計算！百分率と歩合をマスターしよう！（全４問） 【】 みなさん、こんにちは！「さんすうがく」のわかみや先生です。大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います！ … それでは「売買損益」の問題にチャレンジしていきましょう！ この記事を書いている人はこんな人 「さんすうがく」のSPI対策では「SPI＆テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。 なおこの記事で参考にしている参考書は20卒向けのテキストですので、問題番号はあまり気にしないでください。 </noscript><iframe sandbox="allow-popups allow-scripts allow-modals allow-forms allow-same-origin" style="width:120px;height:240px;" marginwidth="0" marginheight="0" scrolling="no" frameborder="0" data-src="//rcm-fe.amazon-adsystem.com/e/cm?lt1=_blank&bc1=000000&IS2=1&bg1=FFFFFF&fc1=000000&lc1=0000FF&t=sansugaku-22&language=ja_JP&o=9&p=8&l=as4&m=amazon&f=ifr&ref=as_ss_li_til&asins=4816373691&linkId=afa07ce8051d33d66e9a207c4f052f61" class="lazyload" > ［118］問題に挑戦！ ［118］原価500円の商品が300個ある。100個を１割引、200個を２割引で売ったときに利益を合計125000円にしたい。定価はいくらにすればよいか。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ 1100円 ［118］解説を見てみよう！ まずは仕入れ値についてみていきましょう。原価が500円で300個あるので仕入れ値は150000円になります。利益が125000円なので売上なければいけない金額は275000円になります。ここで定価を①円と仮定します。仮定すると１割引を○の0.9、２割引を○の0.8になります。これを面積図に直して解いていきましょう！！面積図を書きながら各商品の金額を計算すると、⚪︎の90と⚪︎の160となります。これらを足し合わせて⚪︎の250が275000円と考えることができます。よって275000円÷⚪︎の250＝1100円となります。 SPI対策：損益算の仕組み 売買損益の基礎問題です！ここで一旦売買損益についておさらいしましょう！例えば、ある農家がいたとしましょう。彼はリンゴを育てています。このリンゴを育てるのにかかった費用を“原価”（かかったお金）と呼びます。原価：仕入れたとき（買ったとき）の値段 農家の人たちはその後、別の人にリンゴを売ります。このとき、農家の人が儲けるためには“原価”よりも高い値段で売る必要があります。この価格のことを“定価”（利益を見込んでつける金額）と言います。定価：それに対して利益（もうけたいお金）を出そうと思って売る価格 利益：定価-原価をして儲かったお金 つまり、原価100円のものを定価160円で売ると60円の利益が出る、ということです。定価で売ることで、農家の人はお金がもらえ、リンゴを買った人は欲しかったリンゴを手に入れてみんなハッピー！というわけです。 あわせて読みたい 【中学受験算数】線分図と面積図！後から出発したBが先に出発したAに追いつくまでの時間を求めるには？ 【】 みなさんこんばんは！！「速さ」の問題に今日もチャレンジして行きましょう。本日の問題も「旅人算から復習しましょう。 旅人算ってなに？（復習！） 中学受験算数… ［119］問題に挑戦！ ［119］コーヒーカップを1個100円で400個仕入れた。このうちの１割が割れたとしても、全体で１割以上の利益が出るようにしたい。1個の低下をいくら以上に設定すればいいか。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ 123円 ［119］解説を見てみよう！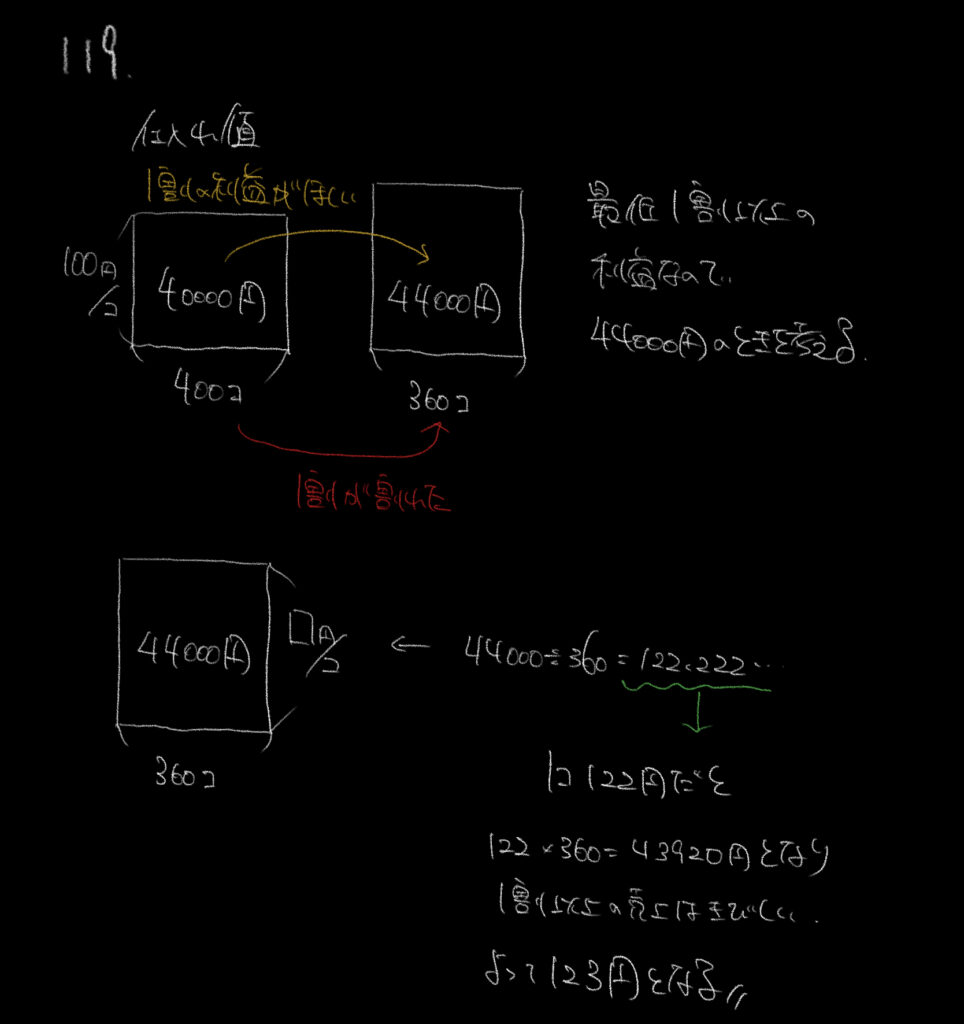 仕入れ値の面積図をかき、そこから情報を付け加えていきましょう。１割の利益を見込んで定価をつけたので売上は40000円×1.1＝44000円、また個数は１割減ったので、400個×0.9=360個になります。ここから計算すると1個あたり122.2222円ならば、基準を満たせるので120円では少し足りません。よって123円が正解となります。 あわせて読みたい 【中学受験算数】日常で見かける売買損益を基本から！まずは利益を見込んでつけた定価から原価の金額を… 【】 みなさんこんばんは！今回も中学受験でよく出てくる算数の問題を解いていきましょう〜今日挑戦」とよばれるお金に関する問題です！さっそく復習からしていきましょ… 百分率、歩合、少数の関係 続いて百分率、歩合の復習です。百分率や歩合はそれぞれ異なった表し方で割合を表します。例えば、百分率は文字通り、全体を100としたときの割合ですが、歩合では10割と表します。ちなみにこれらは数字で表すと１になるので気をつけてください。 わかみや先生 120の100％は12000ではなく、120ですよね？ これは120×１（100％）と無意識に計算しているからです。これらの単位に気をつけて問題に取り組みましょう。 ［120］問題に挑戦！ ［120］1個の原価が400円の品物を150個仕入れ、原価の２割5分の利益を見込んで定価をつけたが80個しか売れなかった。そこで、残りは定価の１割引にして売りつくした。利益は全部でいくらか。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ 11500円 ［120］解説を見てみよう！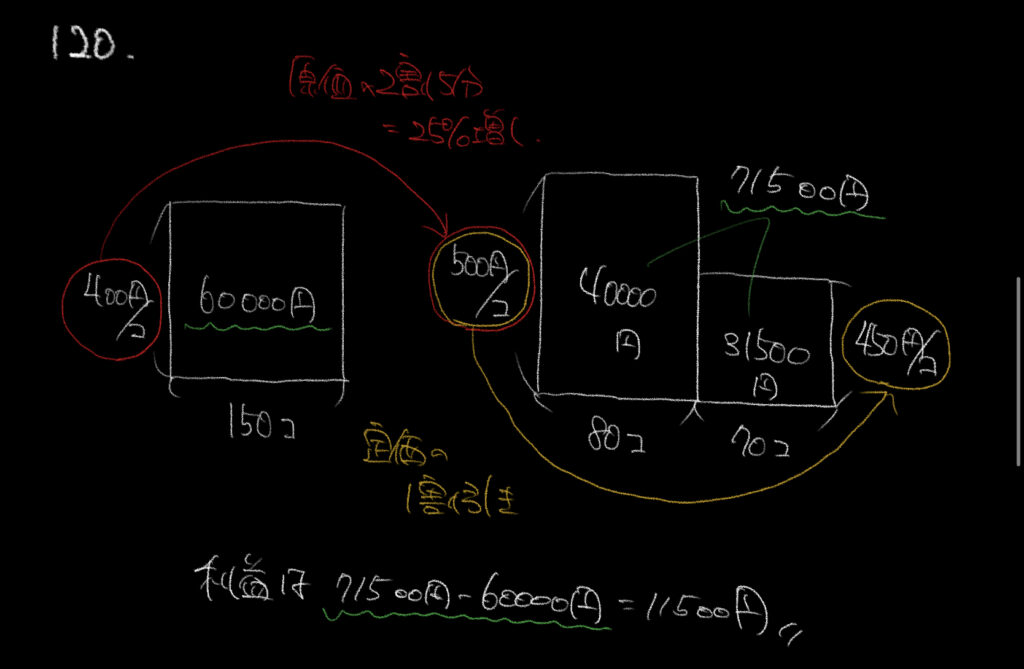 途中から金額を変えたところがポイントでした。原価の２割5分を見込んで定価をつけたので、400円×1.25=500円となります。しかし、そこから１割引いて売り切ったので最終的な価格は450円になります。また個数についても考えてみましょう。初めは80個で売っていて、残りを売り切ったので70個になります。ここから面積図を書いていきましょう！面積図から面積（金額）を求めて利益を計算で求めましょう。元々の仕入れ値は400円×150個で60000円になります。ここから実際に売り上げた金額を求めると、40000円＋31500円＝71500円となり、11500円の利益を出すことができます。 ［121］問題に挑戦！ ［121］品物Pと品物Qをそれぞれ10個ずつ仕入れたところ、18000円かかった。品物Pは原価の２割、品物Qは原価の４割の利益を見込んで販売したところ、完売して売上総額が24000円になった。品物Pの定価はいくらか。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ 720円 ［121］解説を見てみよう！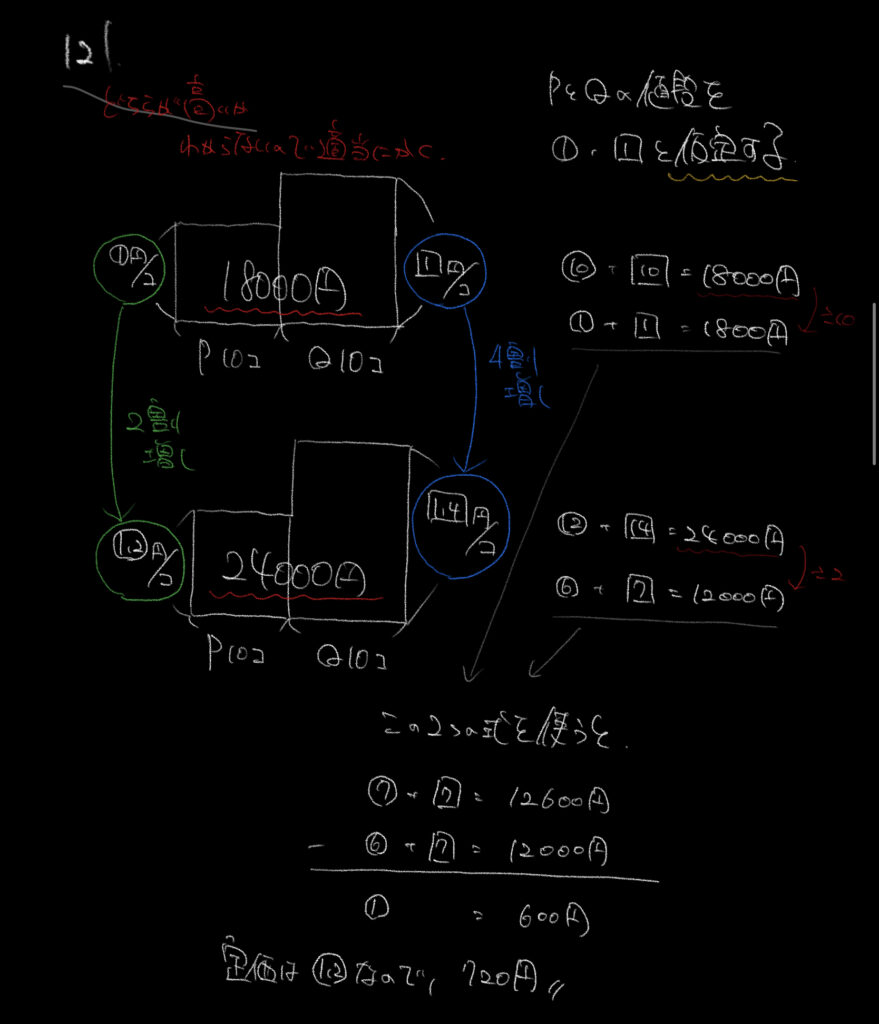 損益算に限った話ではありませんが、SPIや中学受験ではわからない数を仮定することが大事になります。今回はそれの発展で、わからないものを２つの数字で置けるかがポイントになっていました。今回の問題だと１つの記号で問題を解こうとすると思いのほかめんどくさかったりします。こういうとき、めんどくさいなと感じたら記号を２つ使って構いません。ただし、記号（文字）を２つ使うときは２つの文字が入った式を２つ立てる必要があります。そこに気をつけて文字をおきましょう。今回はPとQの値段をそれぞれ⚪︎と◻︎で仮定して解いていきます。２割増、４割増なのでそれぞれの料金を⚪︎の1.2、◻︎の1.4と表すことができます。これを踏まえて２つの式を作り、連立方程式で解きましょう。（小学生は同じ記号を作って、記号を統一していきましょう。）最後に求めたい数をしっかり確認しましょう。今回は①ではなく、○の1.2です！！①を600円と求めましたら1.2倍することで答えを計算できます！ ［122］問題に挑戦！ ［122］1個250円で仕入れた品に２割の利益を見込んで定価をつけたが、売れないので、定価の１割引にして売った。1個あたりの利益はいくらか。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ 20円 ［122］解説を見てみよう！ 極めてシンプルでいい問題だと思います。百分率の基礎ができているか？利益や売り上げの仕組みがわかっているか？そんなことを問われている１問だったと思います。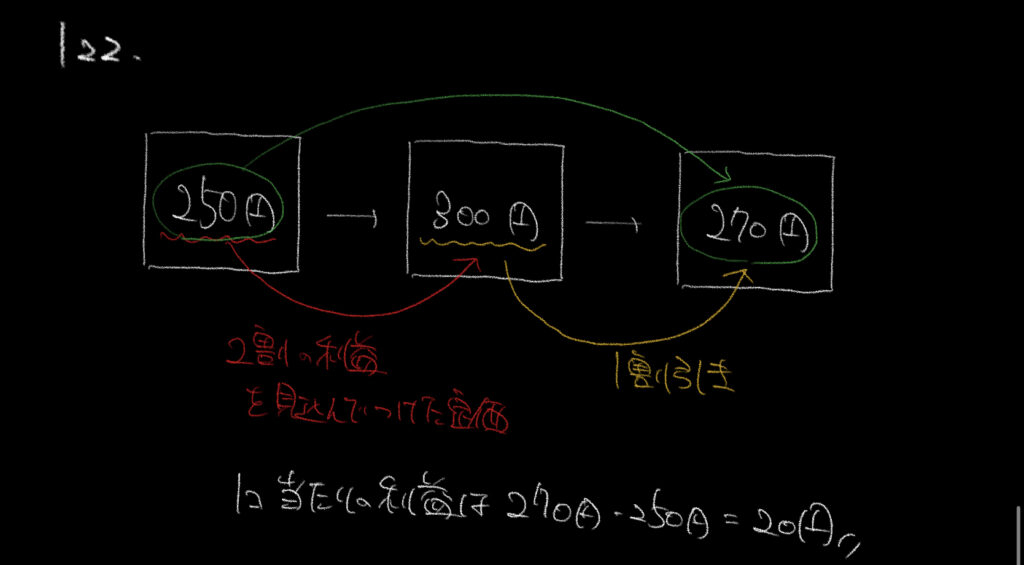もともと250円の品物に、２割の利益を見込んで定価をつけるので250×1.2となります。しかしそこからさらに１割引なので、300円×0.9で270円になります。この図をきちんと書くことができれば、答えを出すのはそう難しくはなかったと思います。 ［123］問題に挑戦！ ［123］ある店では、定価の１割引で売っても原価の２割の利益が出るように定価を設定している。定価が600円の品物の原価はいくらか。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ 450円 ［123］解説を見てみよう！ こちらもしっかりと金額を追って計算していきましょう。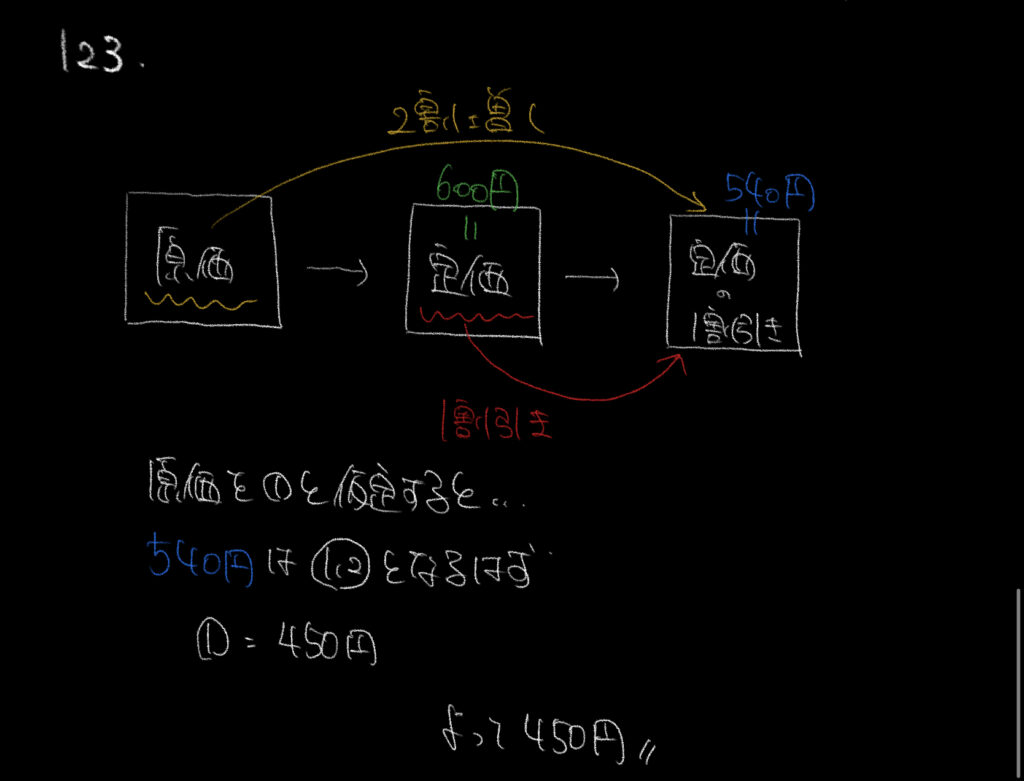原価、定価、値下げ後の定価の３つの価格に分かれています。ここでわかっている情報を書き込んでいきましょう。赤→黄→緑→青の順番で解説が書かれていることをお忘れなく！定価が600円とわかったので、そこからかける情報を記入していきます。すると、値下げした後の金額が540円とわかり、同時にそれが原価を①円とした時の○の1.2円に相当するとわかります。ここから原価を求めていくと450円と出るはずです。ちなみに中学受験でもこれと似た問題があります。小学生には負けないぞ！という方は是非チャレンジしてみてください。 あわせて読みたい 【中学受験攻略】面積図を用いた売買損益の計算方法をイラストで解説！利益から売れ残ったりんごの数を… 【】 今回の和差算の問題は売買損益と呼ばれる考え方が出てきます。売買損益とはものを買ったり、売ったりするような考え方で、受験ではお金が出てくるような問題のこと… ［124］問題に挑戦！ ［124］売値が100円の商品Pの仕入れ値が15％上がったために、利益が１割減った。元の仕入れ値はいくらだったか。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ 40円 ［124］解説を見てみよう！ 簡単そうに見えてあれ？結構難しいな？というタイプの問題でした。落ち着いて解いていきましょう。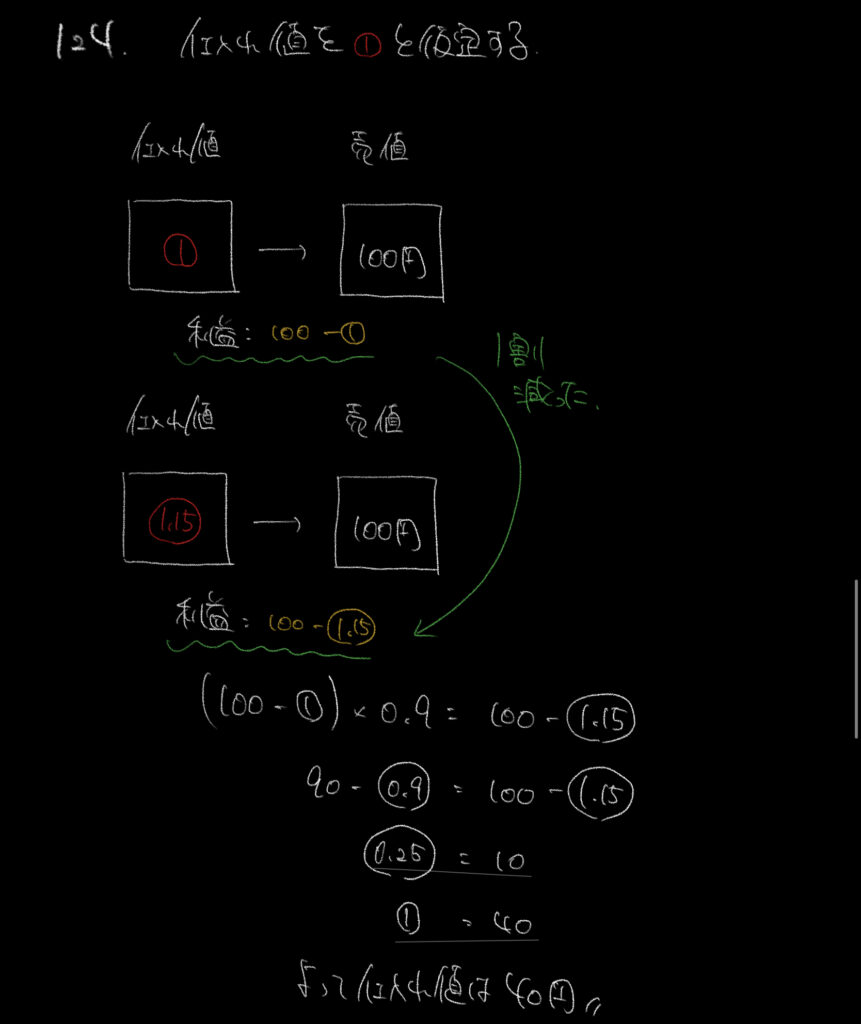損益算の基本は仕入れ値を①と仮定して解いていきます。売値は100円と言われているので利益は100−①円になります。同様に仕入れ値が15％アップしたときの利益も同じように計算すると、（100−○の1.15）円となります。ここの割合が１割減ったので、式を立てることができます。１割減ったということは９割残っているということなので×0.9で計算します。売値が100円のときの利益は100−①円で、１割減って（100−○の1.15）円となっているのでここから計算式を立てます。すると①を40円と求めることができ、答えにたどり着けます。 ［125］問題に挑戦！ ［125］ある衣料品店では、原価の４割の利益を見込んで定価をつけている。①Tシャツの定価が1680円のとき、定価の２割引で販売すると、利益はいくらか。②靴下を定価の２割引で販売すると、利益が72円だった。この靴下の原価はいくらか。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ ①144円②600円 ［125］解説を見てみよう！ ①実際に数字が出てきているので使ってあげましょう。1200円の４割増しなので定価は1200円×1.4＝1680円となります。ここから２割引されるので1680×0.8＝1344円。よって利益は売り上げ−原価なので144円となります。 ②こちらの問題の方が少々手強かったのではないでしょうか。わからない数を仮定して解いていく問題でした。ここで重要なのは何を①とするかでした。しっかりと先の計算ができるように仮定していきましょう。今回、原価を①とおくか、最後の金額を①とおくかではやりやすさが100倍も変わってきます！しっかり見極めて計算していきましょう。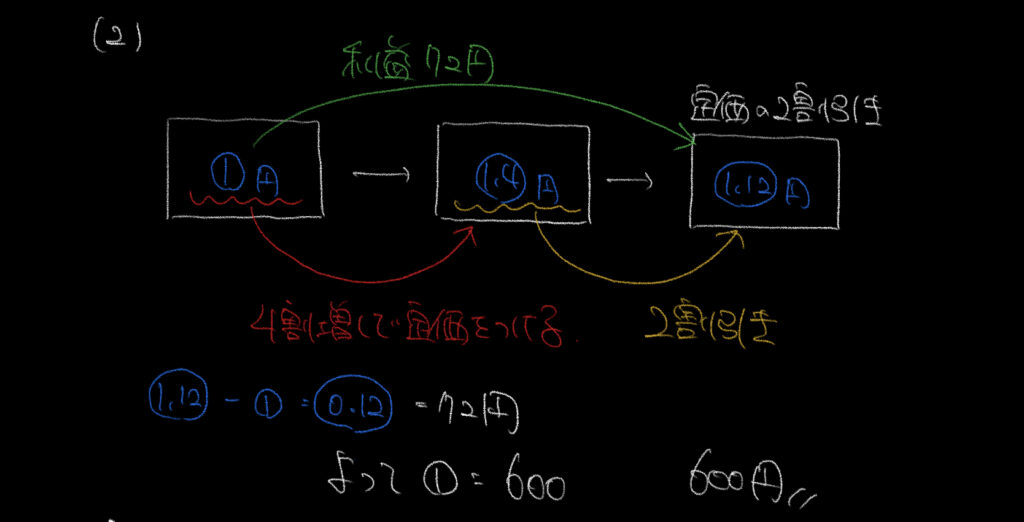今回は原価を①とすると計算がとっても簡単でした。原価を①とすると、４割増しの利益を見込んだ後に２割引を行うので、①×1.4×0.8で最終的な金額は○の1.12となります。今回分かっている情報は利益の72円なので、○の1.12–①＝○の0.12○の0.12=72円と答えを求めていきます！①＝600円！！！ ［126］問題に挑戦！ ［126］ある店では、仕入れ値の35％の利益が出るように定価を設定している。①商品Xを何個か仕入れて、定価999円で販売したところ、全て売り切って合計9324円の利益を得た。商品Xを何個仕入れたか。②商品Yを100個仕入れて、定価378円で60個販売した。残りは値下げして全て売り切りたい。定価で売れたものと合わせて100個の仕入れ値の25％の利益を得るためには、値下げ後の価格をいくらに設定すればよいか。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ ①36個②308円 ［126］解説を見てみよう！ 損益算もこれで最後です。頑張りましょう！！①35％の利益を見込んで定価をつけたということは原価を①とすると定価は○1.35となります。○1.35が999円と言われているので原価は999円÷○1.35＝740円。つまり１個当たりの利益が259円になります。トータルの売り上げが9324円なので、個数を面積図を使って求めると、9324円÷259円＝36個となります。 ②これも一見難しそうに見えますが、なんてことはありません。しっかり図を書いて攻略していきましょう。280円で100個仕入れたので仕入れ値は28000円となります。最終的に25％の利益が欲しいので、28000円×1.25=35000円売り上げたいということがわかります。はじめの60個を378円で売ったので、残りの売りたい金額は全部で12300円（35000円-60個×378円）。残りの個数は40個なので計算すると、12320円÷40個＝1個当たり308円必要と求めることができます。 まとめ 以上がSPIの損益算、いわゆる売買損益でした！！日常的に見かけるものなので、イメージはしやすいのではないかと思いますが、やっぱり頭でやるよりも図を整理して書いた方がわかりやすいと思います。また、基本の基本からやり直したいという方は「割合と比」や面積図から解き直すことをお勧めします！！ あわせて読みたい 【中学受験算数】線分図と面積図！後から出発したBが先に出発したAに追いつくまでの時間を求めるには？ 【】 みなさんこんばんは！！「速さ」の問題に今日もチャレンジして行きましょう。本日の問題も「旅人算から復習しましょう。 旅人算ってなに？（復習！） 中学受験算数… あわせて読みたい 【中学受験攻略】面積図を用いた売買損益の計算方法をイラストで解説！利益から売れ残ったりんごの数を… 【】 今回の和差算の問題は売買損益と呼ばれる考え方が出てきます。売買損益とはものを買ったり、売ったりするような考え方で、受験ではお金が出てくるような問題のこと… 就職活動 SPI 仮定 売買損益 参考になったらぜひシェアお願いします！ URLをコピーしました！ URLをコピーしました！ 【SPI試験徹底対策】割合と比は中学受験のおさらい！記号を使った大学生向け攻略法をご紹介！（全10問） 【SPI試験徹底対策】SPI非言語の「仕事算」必勝法は仮定すること！面積図を活用した攻略法を伝授！！（全４問） 関連記事 【SPI試験徹底対策】並べ方と選び方の問題は場合分け、ボックス、樹形図を使おう！（全8問） 2023年11月26日 【SPI試験徹底対策】席決め、塗り分けは超難問！整理しながら計算するコツを身につけて場合分けの考えで攻略せよ！（全4問） 2023年11月26日 【SPI試験徹底対策】カード、コイン、サイコロ問題突破のカギはお絵かき？中学受験の「数の性質」を使いこなそう！（全４問） 2023年11月26日 【SPI試験徹底対策】円順列、重複の問題攻略法を解説！仕切りの考え方を活用せよ！（全５問） 2023年11月27日 【SPI試験徹底対策】円順列、重複の問題攻略法を解説！場合分けのコツを駆使してケアレスミスをなくそう！（全５問） 2023年11月29日 【SPI試験徹底対策】確率基礎を徹底攻略！解き方のコツは一つ一つの数字の意味を理解すること！（全６問） 2023年11月29日 【SPI試験徹底対策】確率応用はSPI最難関！激ムズ問題多数出題！確率を武器に変えよう（全６問） 2023年12月2日 【SPI試験徹底対策】割合と比は中学受験のおさらい！記号を使った大学生向け攻略法をご紹介！（全10問） 2023年12月3日 解き方から問題に挑戦PとC サイコロ ニュートン算 パップスギュルダンの法則 ピラミッド型 ボックス 中空方陣 仕事算 仕切りの考え方 代金精算 仮定 体積比 余事象 倍数の性質 公約数 円順列 単位 単元攻略 合同 四捨五入 売買損益 展開図 循環小数 投影図 数列の総和 旅人算 植木算 樹形図 歩合 比例反比例 点対称 百分率 相似 相似比 確率 等差数列 等積変形 簡単な例で考える 約数 線対称 補助線 見取図 面積比 １年の日数 ２進法
わかみや先生
