はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います!
今回は「速度算」、いわゆる速さに関する問題です!
この単元はほとんどそのまま中学入試、高校入試で勉強する内容と同じです!
そしてタイトルにあるように、速度算攻略のカギは比と単位です!
この2つのポイントを整理して面積図を書いて解くことで正解に辿り着けます。
復習問題も多く用意しておりますので、こまめに復習しながら問題を解いていきましょう。


この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
[142]問題に挑戦!
答えを見るにはここをクリック!
①時速20km(20km/時)
②時速18km(18km/時)
[142]解説を見てみよう!


①まずは初めの問題では時間に注目していきましょう。
5kmを走るとき出発した瞬間の時間はグラフより、10:37と分かります。
同じようにグラフを見ていくと、到着した時の時間が10:52ということもわかります。
ここから、合計15分で5km走ったと考えられるので時速(1時間で走る距離)は、
15分で5km
1時間(60分)で5×4=20km
よって20km/hであると求めることができます。
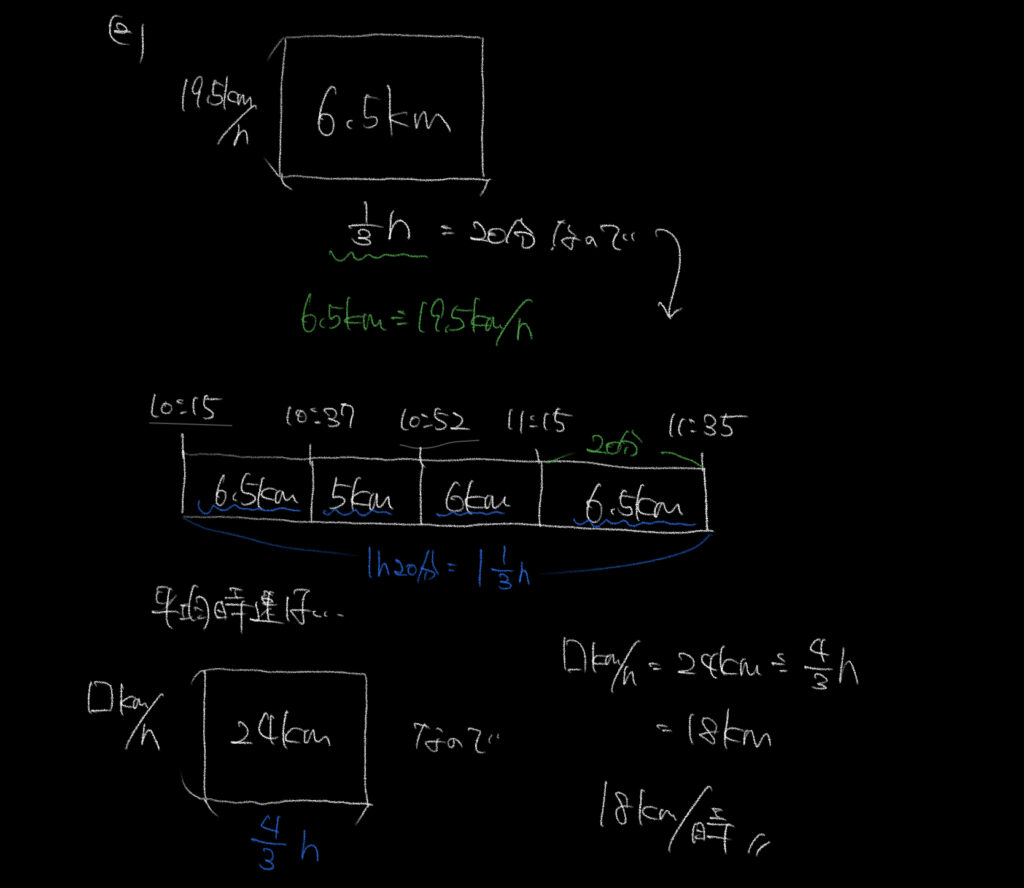

②全区間の平均時速=全部の距離÷全部にかかった時間なので、
最後の到着時間を求めて計算し、平均時速を求めていきましょう。
問題文から第4区の距離が6.5kmであること、走者の平均時速が19.5kmであるとわかります。
これを面積図に直して、面積図より6.5km÷19.5km/h=1/3hで20分
第4区を走りきるまでに20分かかったことがわかります。
これより、全部で24kmを4/3時間(1時間20分)で走ったので、時速を18kmと求められます。
単位を混ぜて計算しないようにしましょう。今回は時速なので、時間の単位を分から時間に変えました!


SPI対策:速度算の考え方
速さの問題、誰しも一度は解いたことがあると思います。
時速だの分速だの、単位もややこしいですし、流水算やら旅人算やら、
「速さ」の単元の中にも細かく内容が異なっていて嫌になってしまいますよね。
分かります。現に私は小学6年生まで時速の単位(km/h)の仕組みがちゃんと分かっていませんでした。
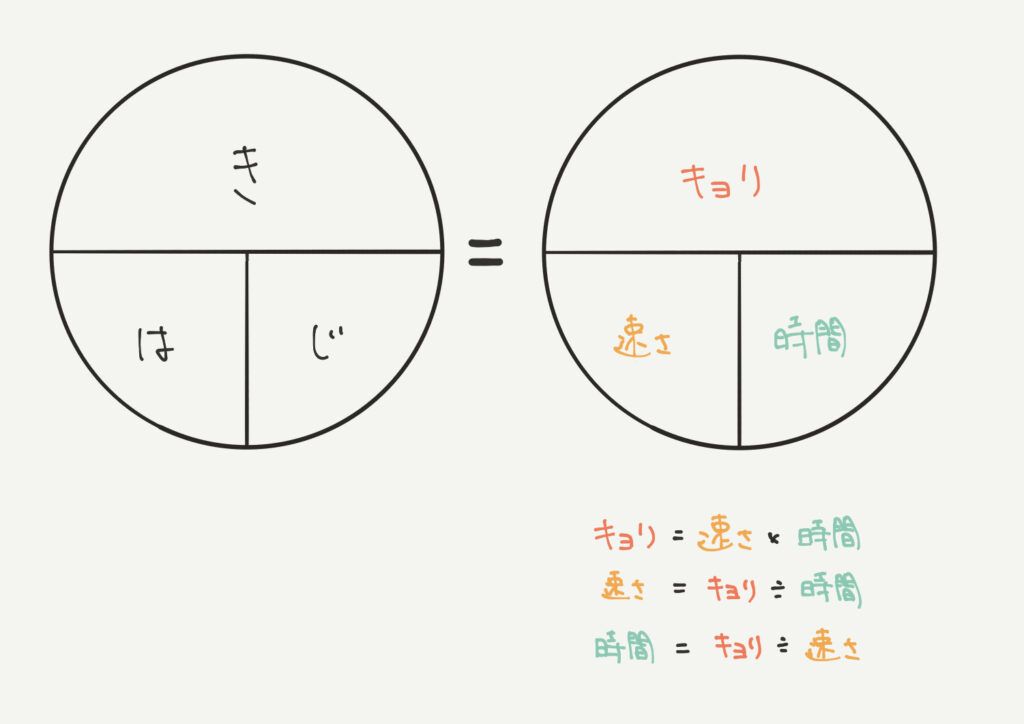
そこで普通き・は・じの考え(中学入試で教わる速さの考え方:きょり、はやさ、じかん)について教わると思います。
しかし私の先生はそのように教えてくれませんでした。そのことは今でも感謝しています。
き・は・じのグラフはあくまでも暗記ベースの勉強法に感じてしまうからです。

算数の問題や数学の問題で、暗記してもいい内容(公式や円周率など)もありますが、
基本的に理解できていないと発展した内容を解くことができません。
私が教わったのは面積図を書くというやり方でした。
距離=面積とし、たての長さ=速さ、横の長さ=時間と考えるやり方です。
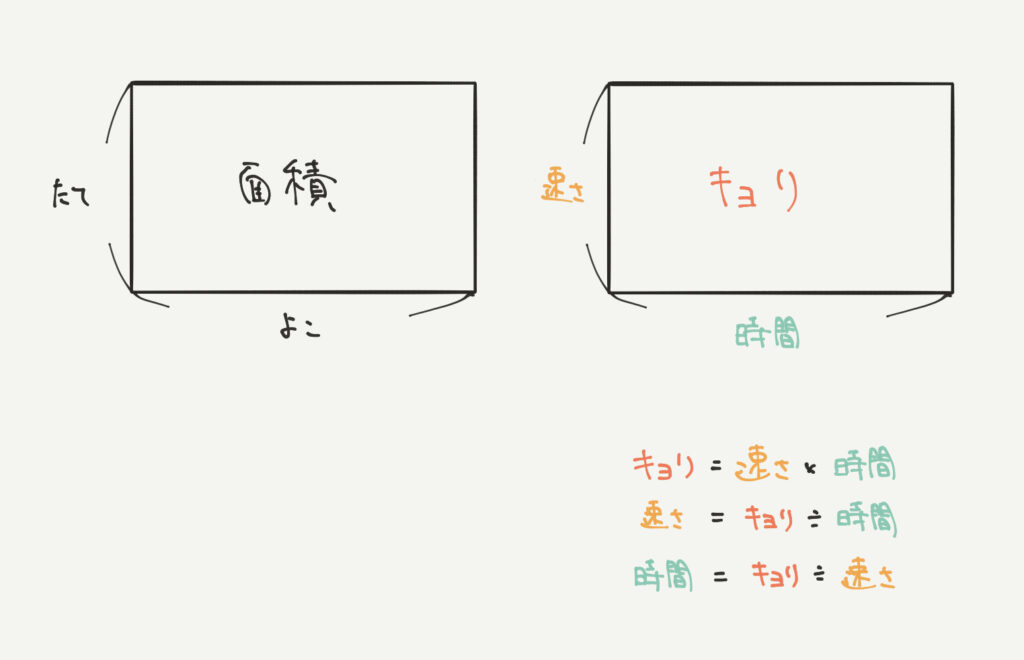

これも暗記だと思われるかもしれませんが、面積図の解き方は速さだけでなく
他の問題でも多用している解き方になります。
なので面積図のやり方だと汎用が効くんですね!
このあたりが面積図の良さだと思います。
この記事で使われる面積図はこれをベースに使用されているので、確認しておいてください!
速さの単元は中学受験用の記事でも書いてあるので、そちらもぜひ参考にしてみてくださいね。

[143]問題に挑戦!
答えを見るにはここをクリック!
①10分で出会う
②32分かかる
[143]解説を見てみよう!


①この問題は一般的に旅人算と呼ばれる問題でした。
旅人算で重要なのは1時間(今回は単位が時間なので1時間となります)で、
どれだけ2人が近づくのか(または遠ざかるのか)を捉えることです。
池の周りを回るこの問題は、1時間で5.4km+3.6km=9kmずつ近づいていきます。
2人が出会う=2人が合計1.5km近づくということなので、面積図に当てはめて計算します。
すると、1.5km÷9km=1/6時間となり、出会う前の時間を10分と求めることができます。





速さの問題で大事なのは出発したとき、出会う時、追いつき追い越される時をイメージすることです。
しかし、頭の中でこれをやってしまうと大変なことになってしまうので、図にしましょう。
速さに自信がないのなら、頭の中でやるのをやめて、絶対に図にすることをお勧めします。
②①と違い今回は単位をmと分で解いています。
注意してみて、自分の解きやすいやり方で解いてみてください。
時速5.4kmは分速90mなので9分あれば、810m先に進みます。
Qの方が遅いので2人が出会う時、Pが1周してQに追いつくことになります。
よって2人の間の距離は810mではなく、1500m−810m=690mということになります。
ここに気をつけましょう。あくまでも早いのはPなのでQが追いつくことはありません。
PはQよりも1分間で進む距離が30m多いので、
毎分30mの割合で2人の差は縮まっていきます。
合計で690m近付けばいいので、690m÷30m/分=23分。
よって23分後に2人が出会うことがわかります。
求めたい答えはPが歩き出してからの時間なので、始めにPが歩いた9分を計算して
9分+23分=32分となります。


[144]問題に挑戦!
答えを見るにはここをクリック!
時速75km(75km/時)
[144]解説を見てみよう!


この問題には2つのポイントがありました。
まず1つ目は出発した時間を揃えて考えるということです。
これは2つ目のポイントにもつながる考えなので、よく確認してください。
電車Xの方が電車Yよりも10分早く進んでいるのでまずはそれを合わせます。
電車Yも10:15に出発したと考えてみましょう。
時速50kmで10分(1/6時間)進んでいるので、進んだ距離は50/6kmになります。
2つの列車は中間地点で出会ったと書いてあるので、
電車Xと電車Yは同じ時間かけてそれぞれ100/6km、25km進んだことになります。
ここで2つ目のポイントです!!
移動した時間が同じとき2つの進んだ距離の比は速さの比に比例します!
2つの列車が同じ時間だけ走って、その距離の比が
100/6:25=2:3となるので、
電車Xの速さ50km/時より、電車Yは75km/時であることがわかります!
速さの比と距離の比
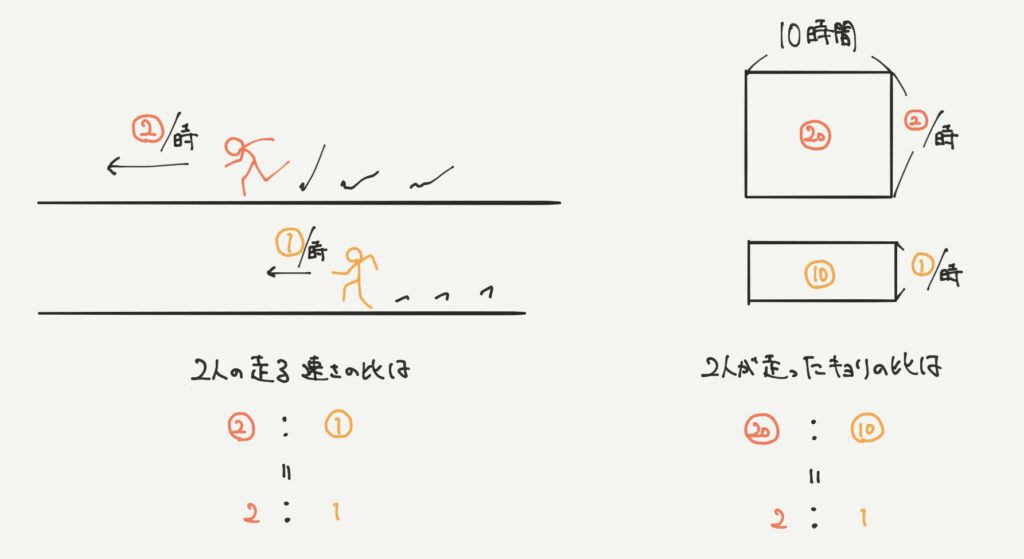

ちょっとさっきの解説でも何言ってるかよくわからんという人は次の例について考えてみましょう。
速さの比が2:1の人がいるとします。
これらの速さを②/時と①/時とし、10時間走ったと仮定します。
すると2人の進んだ距離の比は下のようになります。
どちらも同じ時間だけ速さにかかっているので、距離の比=速さの比となります。
[145]問題に挑戦!
答えを見るにはここをクリック!
時速7.2km(7.2km/時)
[145]解説を見てみよう!
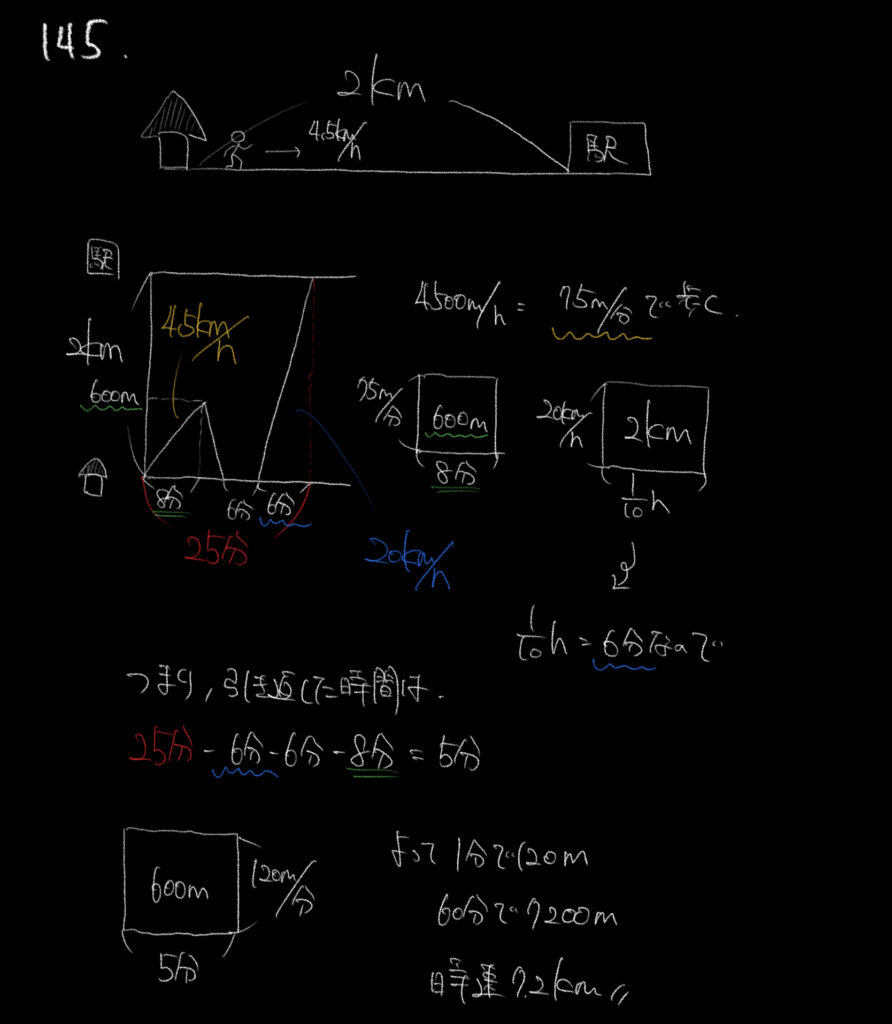

ここで使われている表がダイヤグラムになります。
書く図は特殊ですが、解き方の考えは速さの面積図で対応できるので慌てずにやっていきましょう。
図の書き方は以下の通りです。
縦軸は距離を表しています。基本的に出発点が下にきます。
横軸は時間になります。ここで休んだりした情報を書き込むことができます。
直線は移動している人を表しています。縦と横のメモリに注意して書きましょう。
直線の傾きは速さを表しています。傾きが急であればあるほど、速さは早くなります。
これらを踏まえて、解説の図を見てみましょう。
図の書き方は赤→黄→緑→青です。
基本的に全ての問題で適用されているので、よく覚えておいてください。
単位を揃えて計算することを忘れずに解いていくと、600mの地点で忘れ物に気づいたことがわかります。
ここから取りに帰り(時間はまだわからない)、休憩6分から、6分かけて駅へ向かいます。
ここまで分かれば、
最後に駅に着くまでの25分-6分(休憩)-6分–8分=5分
一回家に忘れ物を取りに帰るときに要した時間が5分とわかるので、
速さは600m÷5分=120m/分となります。
あとは時速に直しましょう!!
1分=120m
60分(1時間)=7200m(7.2km)
7.2km/時となります。


[146]問題に挑戦!
答えを見るにはここをクリック!
①11時25分
②90km/時
[146]解説を見てみよう!


おそらくこの問題が一番難しかったと思います。
そしてこの問題では仮定する考え方も使われます。
それでは早速やっていきましょう。
①[144]の問題でもやったように、まずは出発した時間を揃えるところから始めていきましょう。
時速48kmで5分なので、5分=1/12時間に直して計算します。
すると時速48km×1/12時間=4kmとなり、
4km進んだことがわかるので、11時15分時点の2つの列車の距離は16kmとなります。
これを線分図に書いて、イメージしながら解いていきましょう。
旅人算で重要だったのは2人の近づく速さでしたね。
どちらも48km/時なので、1時間で96km近づきます。
よって16km近づくためには1/6時間=10分必要と求めることができます。
11時15分から10分後なので、11時25分となります。
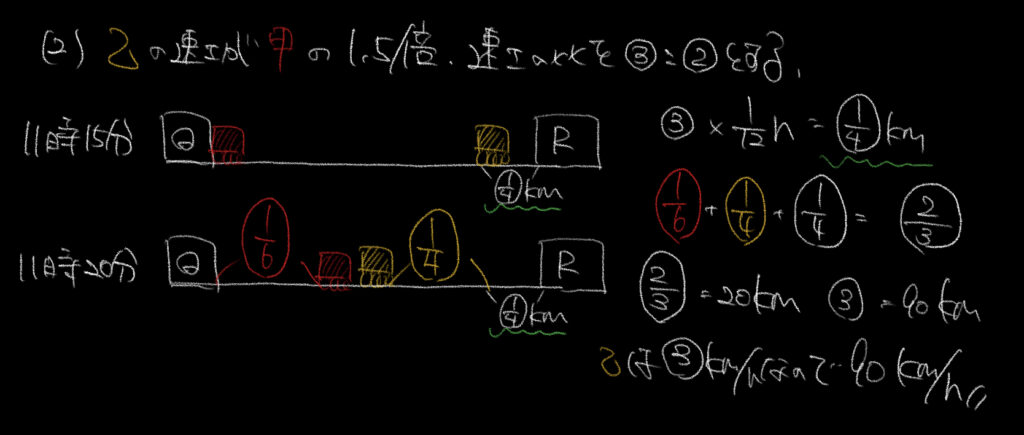
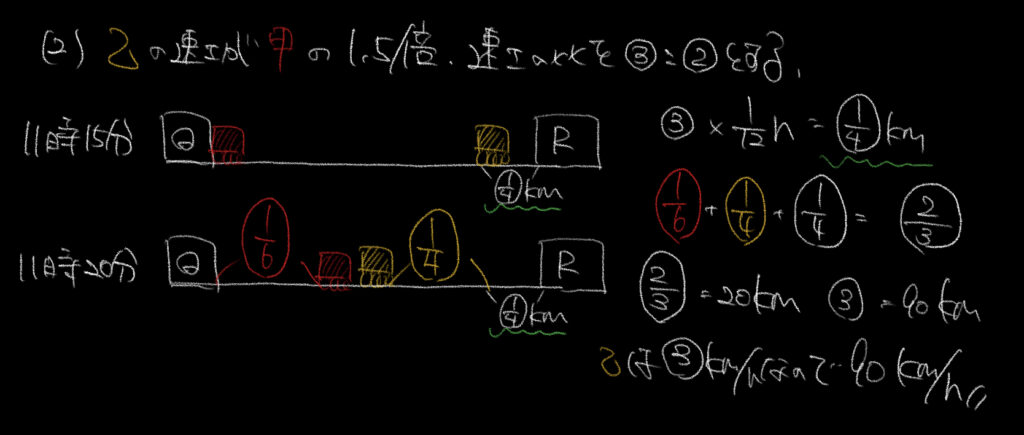
②ここが難しかったのではないかと思います。
しかし、考えはこちらも[144]で一度やった内容です。
速さの比と距離の比は時間が同じであれば一緒になります。
また今回2つの速さが違うので、問題文に合うように仮定していきましょう。
乙が甲の1.5倍の速度で走行するので、
乙の速さを③と仮定すると、甲の速さを②と仮定することができます。
①と同じように乙が5分多く進んでいたので、時間を揃えます。
2人が一緒に進んでいた時間は5分=1/12時間なので、こちらも○を使って距離を表すことができます。
全て足し合わせた○の2/3がQとRの間の距離の20kmなので、
○の2/3=20km
①=30km
求めたい速さは③なので、答えは90km/hとなります。

まとめ
お疲れ様でした!!これで速度算の問題は終わりです〜。
面積図を使った速さの攻略法や、単位の揃え方、時間と距離の比について理解が深まりましたでしょうか??
これはあくまでも個人的な考えですが、難しい問題の方が仮定する考え方を使うと思います。
余裕のある方は是非覚えておいてください。
また、SPIの速度算の問題において、面積図と単位を揃える重要性を理解していただけたと思います。
速さは類題がたくさんあるので是非チャレンジしてみてください!!















