【SPI試験徹底対策】非言語を完全マスター！「集合」の問題は時間をかけてでもベン図をかけ！！（全６問） 2023 12/08 就職活動 SPI 2023年12月8日 目次はじめに わかみや先生 みなさん、こんにちは！「さんすうがく」のわかみや先生です。大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います！ 今回は「集合」に関する問題です！集合の単元は高校のときに勉強された方が多いかもしれませんね。SPIの問題の中でも確率の単元と同じくらいケアレスミスの多いテーマだと思います。今回の目標は「集合」の問題をベン図を使って解いてくことです。ベン図の書き方や考え方含めて丁寧に解決していきますので、一緒に頑張っていきましょう！！ あわせて読みたい 【SPI試験徹底対策】損益算は割合の復習！売買損益の仕組みを理解して面積図を書いて克服していこう！（… 【】 みなさん、こんにちは！「さんすうがく」のわかみや先生です。大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います！ … この記事を書いている人はこんな人 「さんすうがく」のSPI対策では「SPI＆テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。 なおこの記事で参考にしている参考書は20卒向けのテキストですので、問題番号はあまり気にしないでください。 </noscript><iframe sandbox="allow-popups allow-scripts allow-modals allow-forms allow-same-origin" style="width:120px;height:240px;" marginwidth="0" marginheight="0" scrolling="no" frameborder="0" data-src="//rcm-fe.amazon-adsystem.com/e/cm?lt1=_blank&bc1=000000&IS2=1&bg1=FFFFFF&fc1=000000&lc1=0000FF&t=sansugaku-22&language=ja_JP&o=9&p=8&l=as4&m=amazon&f=ifr&ref=as_ss_li_til&asins=4816373691&linkId=afa07ce8051d33d66e9a207c4f052f61" class="lazyload" > ［147］問題に挑戦！ ［147］ある高校の1年生60人に、通学時における電車とバスの利用状況について調査した。電車を利用する人は27人、バスを利用する人は45人で、電車とバスの両方を利用する人はどちらも利用しない人の3倍だった。電車とバスの両方を利用する人は何人か。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ 18人 ［147］解説を見てみよう！ この単元の解説はベン図にかかっています。冒頭でも触れましたが、問題文に書かれていることを素早く図に落とし込めるかが、高得点のカギになります。全体数60人に対して、電車を使う人が27人、バスは45人なので、それをまずはベン図に書きましょう。そして忘れてはいけないのが、電車もバスも使う人がいるということです。なので、ベン図を重ねて書くように注意しましょう！ベン図を重ねて書いた後は最後に、比に注目していきましょう。どちらもやっている人はどちらもやっていない人の3倍なので、やっていない人を①人と仮定すると、やっている人は③人と表せます。ここで気をつけて欲しいのは比と実際の数を混ぜて考えてはいけないことです。実際の人数はわからない、けど比率はわかっているので①人、③人と表せますが、計算する上では記号を混ぜてしまわないように注意していきましょう。バスか電車を使う人＋どちらも使わない人＝全体数なので、27人＋45人−③＋①＝60人となり、①人＝6人と求めることができます。今回知りたいのは③なので18人が正解です。 SPI対策：ベン図の考え方 この集合という単元、すべてのポイントはベン図でした。このベン図をいかに早く正確にかけるかが大事になってきます。和と差に関する問題〈攻略法〉にも同じように書きましたが、ベン図は図の書き方の中でもかなり特殊なタイプだと思います。このベン図は広い範囲の中で複数の事に当てはまる人や数字を数える際に便利です。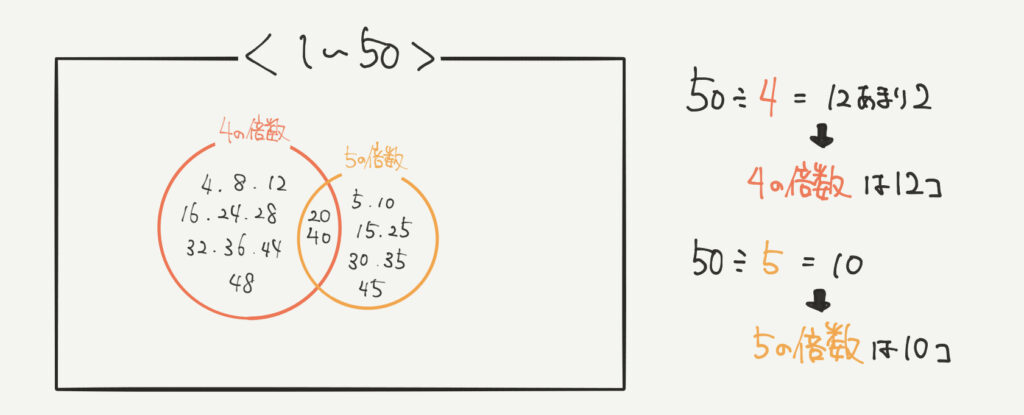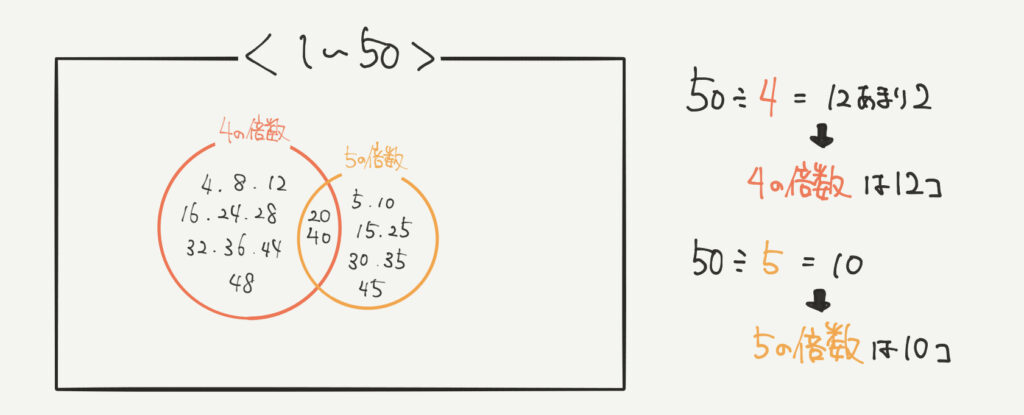 実際に例題を考えてみましょう。1から50までの間に４の倍数または５の倍数はいくつあるか。という問題があったとします。これをいちいち計算して数えるのはめんどくさいですよね。そこでベン図を使って攻略していきます。 この図だと1〜50までの4の倍数と5の倍数を書いています。もちろん1〜50の中には4の倍数でも5の倍数でもない数があります。逆に4の倍数でもあり、5の倍数でもある数（20、40）などもあります。他に４の倍数だけで5の倍数でない数や５の倍数だけど4の倍数じゃない数があります。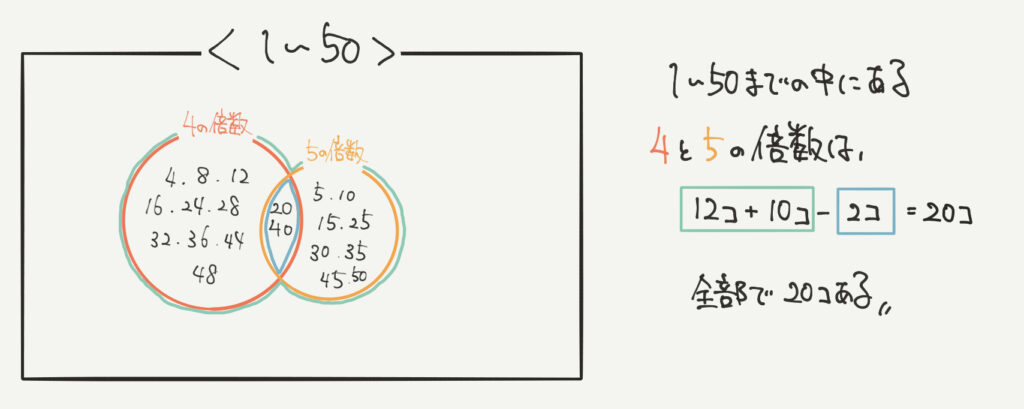これらをそれぞれ求めて解いていく流れとなります。ただし、4の倍数＋5の倍数とやってしまうと、青い部分を重複して数えてしまうので、黄＋緑−青＝4か、5の倍数となります。 ［148］問題に挑戦！ ［148］50人が20問のテストを２回受けた。10問以上正解した人は１回目が42人、２回目が43人だった。1回目も2回目も正解が10問未満だった人が3人だったとき、1回目も2回目も10問以上正解した人は何人か。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ 38人 ［148］解説を見てみよう！ 問題文が少し複雑に感じてしまうかもしれませんが、こちらの問題も図を書いてしまえば簡単です。ポイントとなるのが1回目も2回目も正解が10問未満だった人が3人という部分です。これを言い換えると、1回目か2回目を10問以上正解した人が47人いるということになります。これがこの問題を解く上でのヒントになります。ベン図には1回目で10問以上正解した人、2回目で10問以上正解した人を書きます。そしてもちろん、1回目も2回目も10問以上正解している人がいることもお忘れなく！1回目か2回目を10問以上正解した人が47人という情報、そして黄色の部分全体＝42＋43−□ということから、両方正解している人が38人いることがわかると思います。この黄色の部分の面積の求め方は１問前の［147］を参考にしてみてください。 ［149］問題に挑戦！ ［149］ある地域の中学校300人を対象に、季節とスポーツについてアンケートを行った。下の表は、その結果の一部である。①夏が好きで、かつ水泳が得意と答えた人が150人いた。夏がきらいで、かつ水泳が得意でないと答えた人は何人か。②夏も冬もきらいだと答えた人が10人いた。夏と冬のいずれか一方だけ好きと答えた人は何人か。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ ①30人②70人 ［149］解説を見てみよう！ さっきよりも少し難易度の高い問題だったと思います。ここでもベン図を使って解いていきましょう。問題ごとにベン図を書き直していますがアンケートの内容が違うので、しっかりと書き分けるようにしていきましょう。それではやっていきましょう！（解説の簡略化のため、水泳が得意＝水泳が好きとしています。）①問題文より、全体数は300人とすぐにわかります。どちらも好きではない人を求めるためには、夏と水泳のどちらか、またはどちらも好きな赤い部分の人数を求めてあげる必要があります。夏が好きな人は240人、また水泳が好きな人は180人、そしてどちらも好きな人が150人とすでに必要な情報は揃っているので、知りたい赤い部分は240＋180−150＝270人と求めることができます！ ②今度はどちらも嫌いの人がすでにわかっていて、そこから逆算してどちらも好きな人数を求めるという問題でした。300人＝どちらか、または両方好きな人＋どちらも嫌いな人なので300＝240＋270−□＋10となります。ここから□＝70人と求まるはずです。 あわせて読みたい 【中学受験攻略】数の性質を軽々クリア – 分数の理解から実践問題の解き方まで徹底ガイド！ 【はじめに】 みなさんこんばんは！！「さんすうがく」の赤い小人です。「 数の性質 」、今回はベン図の考え方を使う問題が出ます。 確か前もベン図の問題を解いたよう… ［150］問題に挑戦！ ［150］会員100人のうち、土曜日の集会の参加者は56人、不参加者は44人である。また、日曜日の集会の参加者は69人、不参加者は31人である。①土日の両日とも参加できない人は最も多くて何人か。②土日は参加できず、日曜日だけ参加できる人が13人のとき、両日とも参加できる人は何人か。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ ①31人②56人 ［150］解説を見てみよう！ ベン図でも解けましたが、①のような最も多い場合の人数などは仮定の考えを使って解くようにしましょう。①解説でも書きましたが、考えられる最大の数は土曜日に来なかった44人のうち31人が日曜日に来なかったときです。こう考えると、そこまで難しくはないですよね？ ②こちらもよく考えれば難しくはない問題です。じっくり考えていきましょう。日曜日に参加した69人のうち、日曜日だけの人が13人いると問題文に書かれています。では残りの人はどのような人でしょうか？残りの人は日曜日だけでなく、土曜日も参加した人ということになりますね。よって求めたい答えは69−13＝56人です。さて、次からベン図の難易度が格段に跳ね上がります。３つの円が出てくるベン図です！さあやっていきましょう！ あわせて読みたい 【中学受験攻略】 数の性質を理解しよう！3桁の整数の中で19の倍数はどれだけ存在する？ 【はじめに】 みなさんこんばんは！！「さんすうがく」の赤い小人です。 今日も「 数の性質 」の問題ですか？？ はい！それに加えて今回はベン図 を使って解説していま… ［151］問題に挑戦！ ［151］社内の50人のうち、P新聞を読む人は28人、Q新聞を読む人は20人、R新聞を読む人は14人で、どれも読まないという人はいなかった。①P新聞もQ新聞も読む人は8人だった。R新聞だけ読む人は何人か。②前問の条件に加えて、3紙全部を読む人が1人だけいた。2紙以上を読む人は何人か。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ ①10人②11人 ［151］解説を見てみよう！ わかみや先生 はい。難易度爆上げです。 ３つの円が出てくる問題でした。それぞれに重なっている部分があること、そして３つの円が重なっている部分があることを忘れずに慎重に図を書いていきましょう。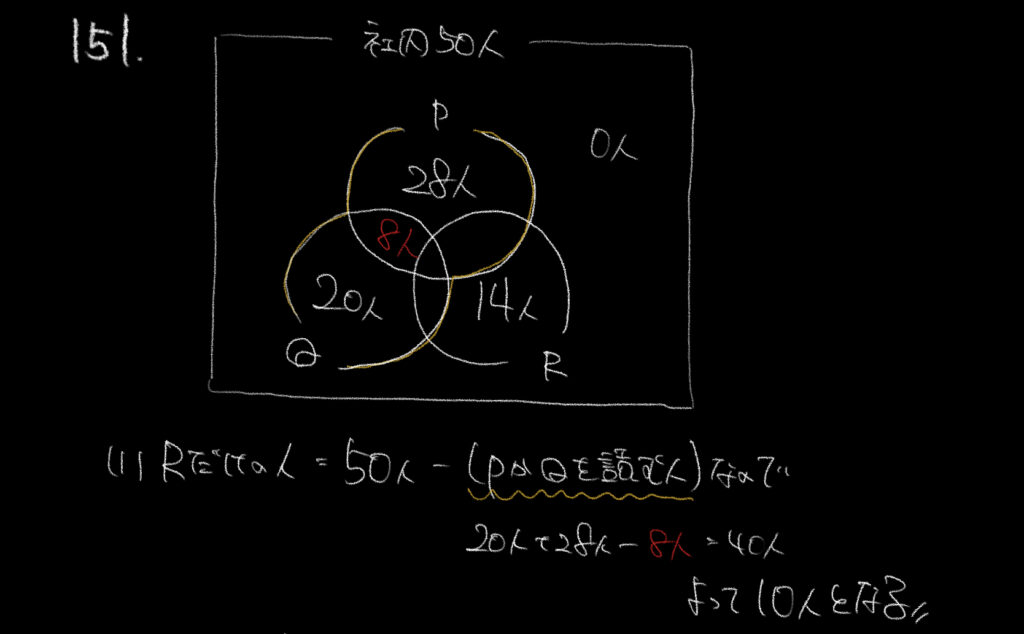①Rだけの人。このだけというのがポイントです。これはつまりRとP、RとQの人は含みませんので注意してください。Rだけの人を求めるには全体の人数から、PまたはQを含む人を引けばいいので、全体−PまたはQを含む人＝Rだけの人50−（20＋28−8）＝10人よってRだけの人数は10人と求められます。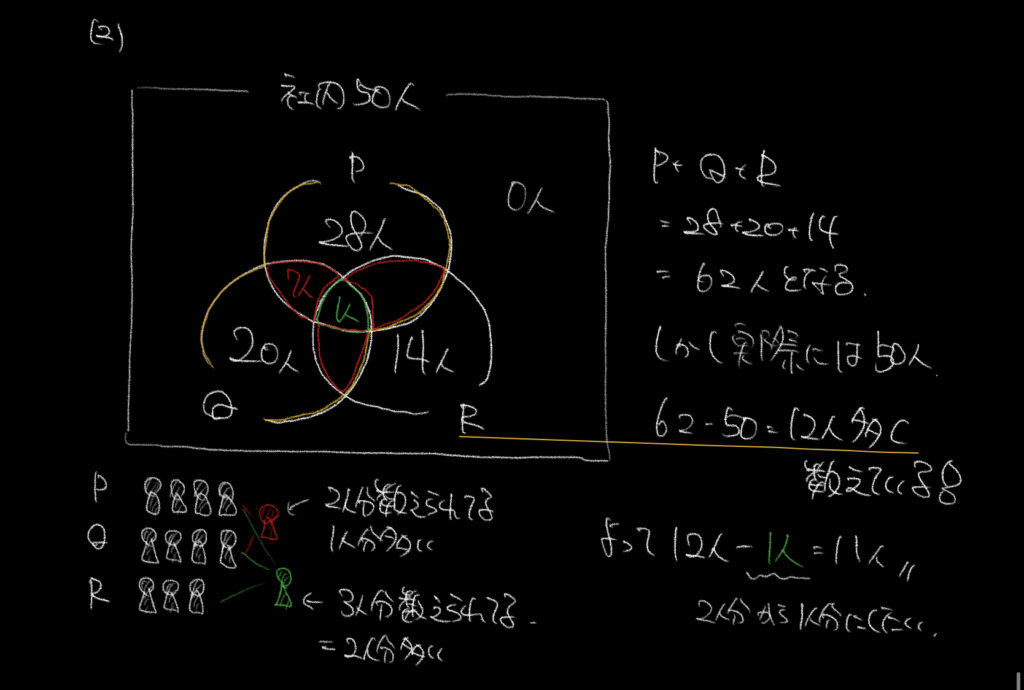 ②この問題が難しい理由は、３つの円に重複する人がいたからでした。ここを理解できるかできないかで、集合に対する苦手意識が大きく変わると思います。まずはこの重複について考えましょう。12人の重複のうち、３個の円に入っている1人がさらに1回多く数えられているので、実際の人数は12−1＝11人となります。 わかみや先生 どういうことかわからない人も安心してください！下のセクションで詳しく解説しています！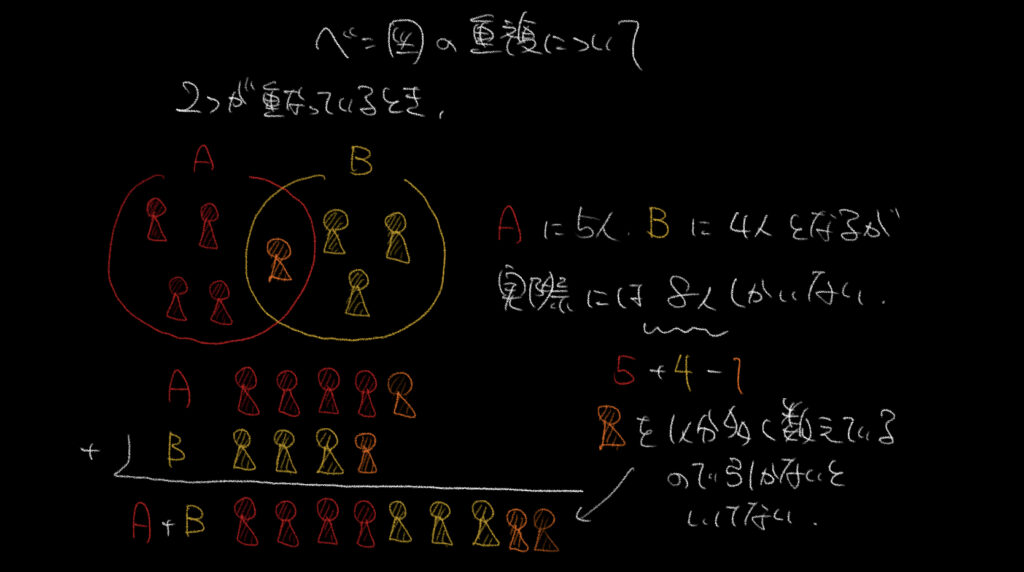 SPIの最難関問題：ベン図の重複について いつもよりもわかりやすく、色を意識して書きました。見にくかったらすいません。まずは２つの円が重複しているとき、Aには5人、Bには4人がいます。しかし、実際にいる人は5＋4＝9人ではなく、9人−1人＝8人になります。これはオレンジの人を2回数えてしまっているから起こるミスです。なので数えるときは5＋4−1＝8人とやってあげましょう。ここまでは大丈夫かと思います。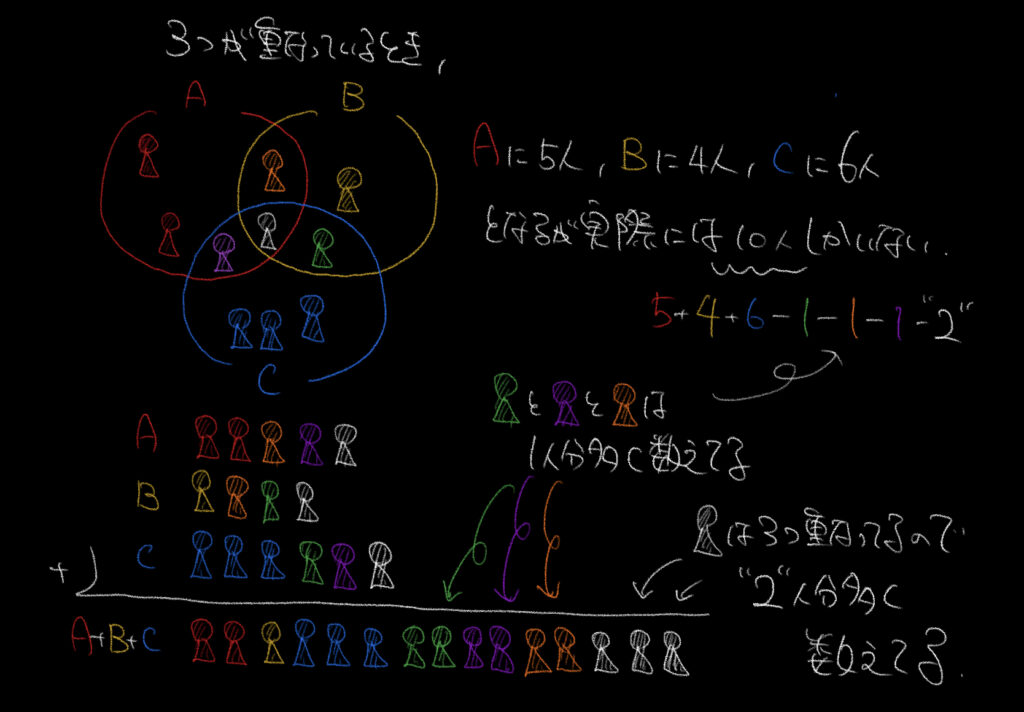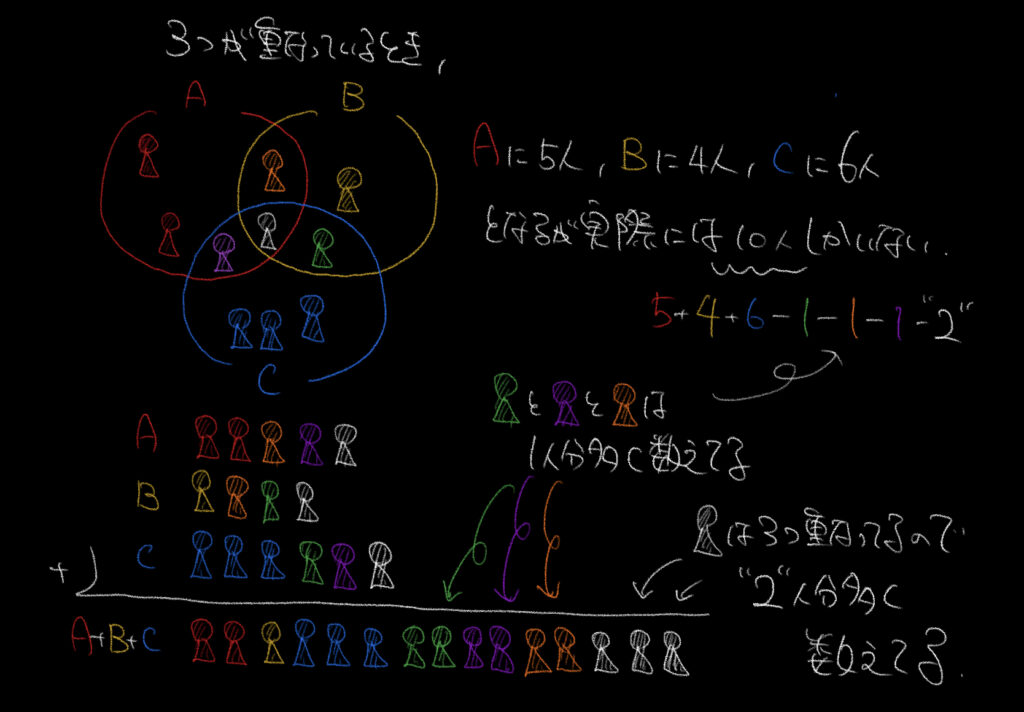 ここから、３つが重なっているときのことを考えましょう。同じようにAには5人、Bには4人、そしてCには6人いますね。全部足すと15人になるはずが、実際には10人しかいません。これはオレンジ、緑、紫の人を2回数えてしまっているから、また黒の人を3回数えてしまっているからです！図を見るとよくわかると思います。なので、２個の円が重複してしまっているなら１引いてあげなければいけませんし、３個の円が重複しているなら2引いてあげないといけません！これがベン図の重複についての考え方でした。 あわせて読みたい 【中学受験攻略】算数で差をつける！3でも4でも割り切れない数を一瞬で計算する方法！ 【】 みなさんこんにちは！まもなく夏休みも終わりですね。みなさん宿題は終わっていますか？僕は読書感想文が苦手で最後の1日までやらずに後悔してみましょう！ 「数の… ［152］問題に挑戦！ ［152］150冊の本を分類したところ、心理学に分類できる本が70冊、教育学に分類できる本が40冊、社会学に分類できる本が64冊あった。①心理学と教育学の両方に分類できる本が15冊あった。心理学には分類できないが教育学に分類できる本は何冊か。②①の条件に加えて、社会学だけに分類できる本は34冊あった。心理学、教育学、社会学のいずれも分類できない本は何冊か。③①と②の条件に加えて、心理学、教育学、社会学すべてに分類できる本は、心理学と社会学だけに分類できる本の3倍、教育学と社会学だけに分類できる本の半分であった。すべてに分類できる本は何冊か。 SPI＆テストセンター超実践問題集/ナツメ社 答えを見るにはここをクリック！ ①25冊②21冊③9冊 ［152］解説を見てみよう！ 毎度のように最後が一番むずい問題です。頑張っていきましょう！！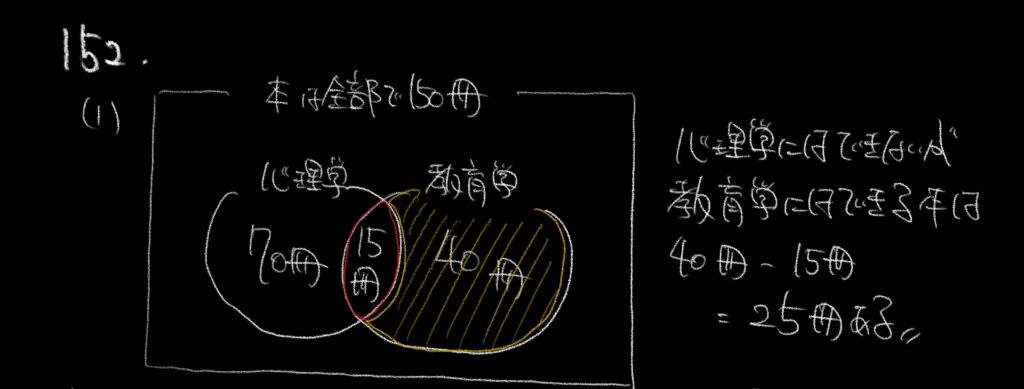①これは比較的簡単な問題。ベン図を２個書いて求めていきましょう。心理学に分類はできないけど、教育学に分類はできる本は教育学の本全体から教育学でもあり、心理学でもある本を引けばいいので40−15＝25冊となります。 わかみや先生 解説をよ〜くを読んでください！！！！絶対理解できるはずです！ ②社会学のみが34冊、残りの心理学または教育学に分類されるのは70＋40−15＝95冊あることがわかります。全部足して、いずれかに分類される本が95＋34＝129冊となります。よって、どれにも当てはまらない本の数は150−129＝21冊です。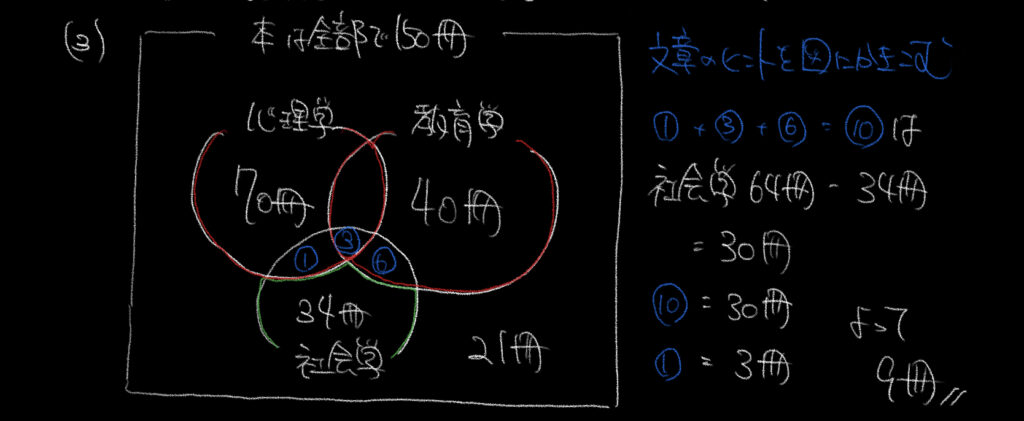 ③文章に書かれている比の情報を○としてベン図に書き込みましょう。①、③、⑥を図に書き込めましたか？ケアレスミスをしてしまうので、気をつけましょう。問題文より、社会学に分類できる本は64冊、社会学のみに分類できる本は34冊あるので、⑩＝30冊とわかります。ここから⑩＝30冊①＝3冊となって、③＝9人とわかります。 まとめ 以上がSPIの「集合」の問題でした！出来るだけわかりやすいように解説を作成しましたがどうでしたか？少しは苦手意識がなくなったことを祈ります！！集合ではどうしても重複の部分でこんがらがってしまう人が多いので、いかにそこを克服するかがカギです。まずは時間をかけてでもベン図を書くこと。これに尽きます。初めから素早く解ける人なんていません。地道に書き続けることが大事です。３個の円の重複までしっかり理解できれば、集合の問題で苦労することはないと思いますので、ぜひ根気よく復習してみてください。 就職活動 SPI 仮定 ベン図 参考になったらぜひシェアお願いします！ URLをコピーしました！ URLをコピーしました！ 【SPI試験徹底対策】非言語の「速度算」攻略のカギは比と単位！速さの面積図を書いて解き進めよう！（全５問） 【SPI試験徹底対策】SPI非言語の「特殊算」は中学数学の総復習！基礎力を固めて臨機応変に解き進め！（全８問） 関連記事 【SPI試験徹底対策】並べ方と選び方の問題は場合分け、ボックス、樹形図を使おう！（全8問） 2023年11月26日 【SPI試験徹底対策】席決め、塗り分けは超難問！整理しながら計算するコツを身につけて場合分けの考えで攻略せよ！（全4問） 2023年11月26日 【SPI試験徹底対策】カード、コイン、サイコロ問題突破のカギはお絵かき？中学受験の「数の性質」を使いこなそう！（全４問） 2023年11月26日 【SPI試験徹底対策】円順列、重複の問題攻略法を解説！仕切りの考え方を活用せよ！（全５問） 2023年11月27日 【SPI試験徹底対策】円順列、重複の問題攻略法を解説！場合分けのコツを駆使してケアレスミスをなくそう！（全５問） 2023年11月29日 【SPI試験徹底対策】確率基礎を徹底攻略！解き方のコツは一つ一つの数字の意味を理解すること！（全６問） 2023年11月29日 【SPI試験徹底対策】確率応用はSPI最難関！激ムズ問題多数出題！確率を武器に変えよう（全６問） 2023年12月2日 【SPI試験徹底対策】割合と比は中学受験のおさらい！記号を使った大学生向け攻略法をご紹介！（全10問） 2023年12月3日 解き方から問題に挑戦PとC サイコロ ニュートン算 パップスギュルダンの法則 ピラミッド型 ボックス 中空方陣 仕事算 仕切りの考え方 代金精算 仮定 体積比 余事象 倍数の性質 公約数 円順列 単位 単元攻略 合同 四捨五入 売買損益 展開図 循環小数 投影図 数列の総和 旅人算 植木算 樹形図 歩合 比例反比例 点対称 百分率 相似 相似比 確率 等差数列 等積変形 簡単な例で考える 約数 線対称 補助線 見取図 面積比 １年の日数 ２進法
わかみや先生
