はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います!
今回一緒に勉強する単元は「特殊算」と呼ばれる問題です!
特殊、といっても問題の1つ1つは昔みなさんが勉強したであろう
「植木算」や「推理算」などの問題の集まりです。
これまで勉強した算数や数学の基礎知識を使いながら、問題を解いていきましょう!


この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。


SPI対策:特殊算の考え方
特殊算には基本的な解き方は決まっていなく、臨機応変に対処しなければいけません。
そのため、今までの基礎知識が試される場になるでしょう。
〇〇算は□□のやり方、△△算は◉◉のやり方、と
解き方を丸暗記してしまうのが成績が伸び悩む子の典型です。
それでは応用問題に対応できません。
〇〇算は□□のやり方が一般的だけど、なぜそうなのか?
他に方法はないのか?このやり方でもできるんじゃないか?など
試行錯誤をしながら解き進めることが基礎力アップにつながると思います。
今回の単元はそのような各単元の確認と思って解いてみてください。
今までの総復習となる今回の単元、出てくる思考法と解法を先にチラ見せします!
非言語攻略のカギ①:仮定すること
こちらはもうお馴染みですが、わからないことがあれば仮定する考えを使って解いていきましょう。
わからない数字が出てきた際に、もし⚪︎⚪︎がXXだったら〜と解き進める考えのことでしたね!
これまでのSPI非言語対策でもたくさん使った考え方になります!
仕事算:もし1人が1日で行う仕事量が①と仮定すると〜他の人の仕事量は⚪︎になる、など
損益算:原価のX割の利益を見込んで低下をつけたので、原価を①と仮定すると〜定価は⚪︎になる、など




非言語攻略のカギ②:面積図/平均の考え
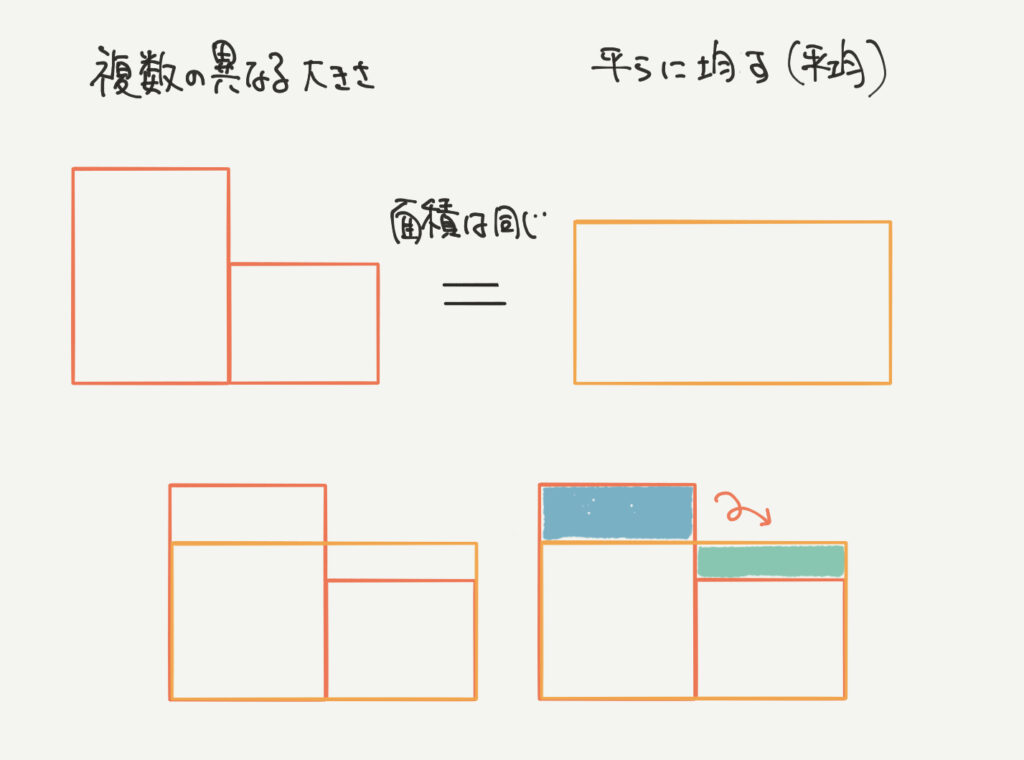

続いて面積図の中の平均の考えです。
平均であれば、黄色の面積と赤色の面積が等しくなるはずなので、
青と緑の面積も等しくなるはず、という考えでした。


非言語攻略のカギ③:線分図
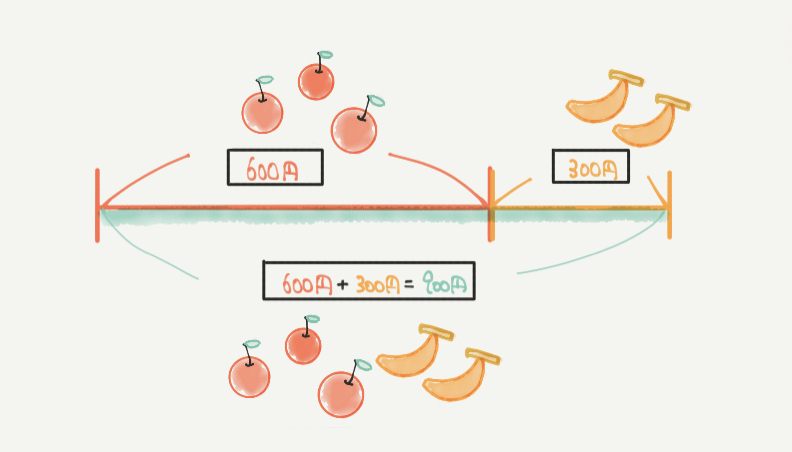

何かと何かを比較する上で線分図はとても有効です。
SPIではxと使っても解けますが、時間がなくて焦ってしまったり、
ケアレスミスを防ぐ上では線分図はとても便利です。
時間に余裕があるなら復習しておきましょう。必ず役に立ちます。

非言語攻略のカギ④:植木算
植木算の考えで引っかかりやすいのが木の本数と間隔の数が違うというものでしたね。
下の例で見ていきましょう。
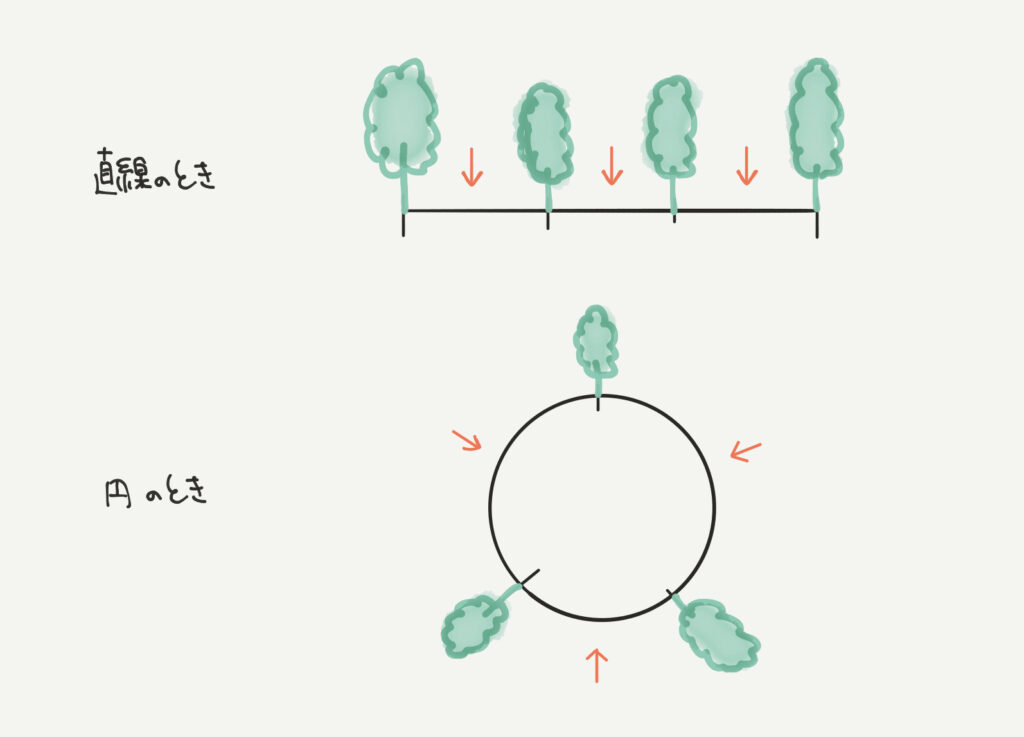

木の数が4本なのに対して間隔は3つですね。
つまり、計算で間隔が3つと分かれば、木の数は3+1=4本、
逆に木の数が4本と分かれば、間の数が3つとわかります。
逆に円のように道路が一周しているときは、木の数=間隔になります。







ここからは実践問題にチャレンジしていきましょう!
[161]問題に挑戦!
答えを見るにはここをクリック!
最大8個
[161]解説を見てみよう!


一番多く90円のお菓子を買う場合、
金額の合計は12個×90円=1080円になります。
しかしこれでは上限を上回ってしまうので、ここから一つずつ減らしていきましょう。
表を書くおさらいです。
計算でも解けますがミスを減らしたいのであれば、表を書いていきましょう。
そこまで時間もかかりませんしね。
90円が1つ減って、70円が増えるので金額は20円ずつ減っていきます。
表から90円が8個の時にぴったり1000円になることがわかります。
この問題は下の記事にある輪投げの問題とそっくりでしたね。
気になる方はぜひチェックしてみてください!


[162]問題に挑戦!
答えを見るにはここをクリック!
2枚
[162]解説を見てみよう!


ここでの重要なポイントは文章の中にある全種類合わせてという点です。
これは言い換えると1つは必ず使うということになるので、13枚のうち、4枚は決まっています。
よって考えなければいけないのは、残った9枚で790円を作れる組み合わせです。
ここからは「調べと推理」と似ています。
選択肢を徐々に減らしていくように仮定し、検証していきます。
まずは枚数が0か1の500円玉を1枚あると仮定します。
残りの金額とお金から見て、500円玉はほぼあると考えられたので1枚で仮定しました。
次に注目できるのが10円玉です。790円を作るためには10円玉が最低4枚必要になります。
(10円玉4枚+50円玉1枚で90円が作れます。)
ここから残りの100円、50円の組み合わせを考えていくと、250円の組み合わせを見つけることができます。
このように一つ一つの可能性を検証することが大事でした。
また、全種類という単語に注目する考えは場合の数でもやりましたね!


上の記事の[82]②がそっくり問題になっています!
次の問題は少し工夫して問題をわかりやすくしていきます!
[163]問題に挑戦!
答えを見るにはここをクリック!
14個
[163]解説を見てみよう!
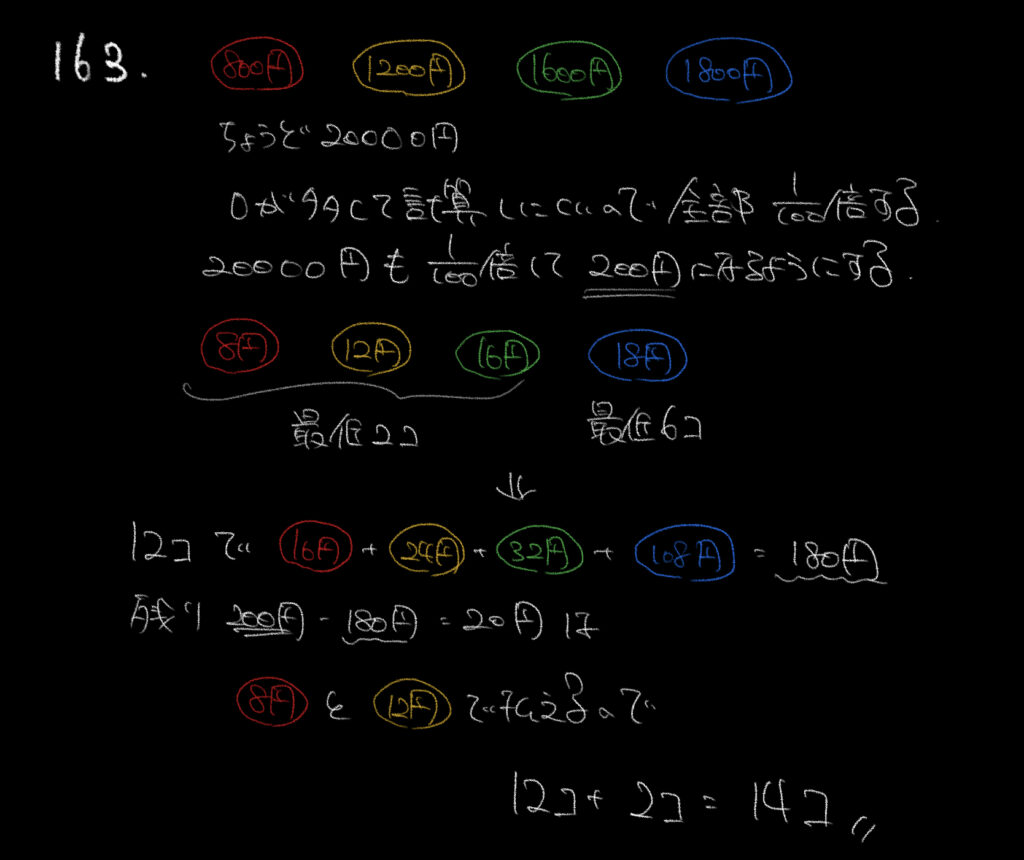

この問題、解説にもある通り0が多くて嫌ですよね。
そういう時は全部を1/100倍して簡単な数にして考えてみましょう。
するとこの問題は8円、12円、16円、18円を組み合わせて200円を作るという問題になります。
そして18円のぬいぐるみを最低6個、それ以外を最低2個入れて考えるとこの時点でもう180円。
200円を作りたいので、残りの20円分の組み合わせを考える必要がありました。
残り20円分を買う組み合わせを探すと8円、12円の組み合わせがあるので2枚買うことができます。
よって合計枚数は問題文で指定されている12枚+2枚=14枚となります。
問題文の条件をそのまま簡単にすることは計算スピードを早めることにつながります。
しかし、この簡単にするやり方を間違えてしまうと即間違えてしまうので、
問題文を簡単にするときはしっかりと確認してから行うようにしましょう。

[164]問題に挑戦!
答えを見るにはここをクリック!
4000個
[164]解説を見てみよう!
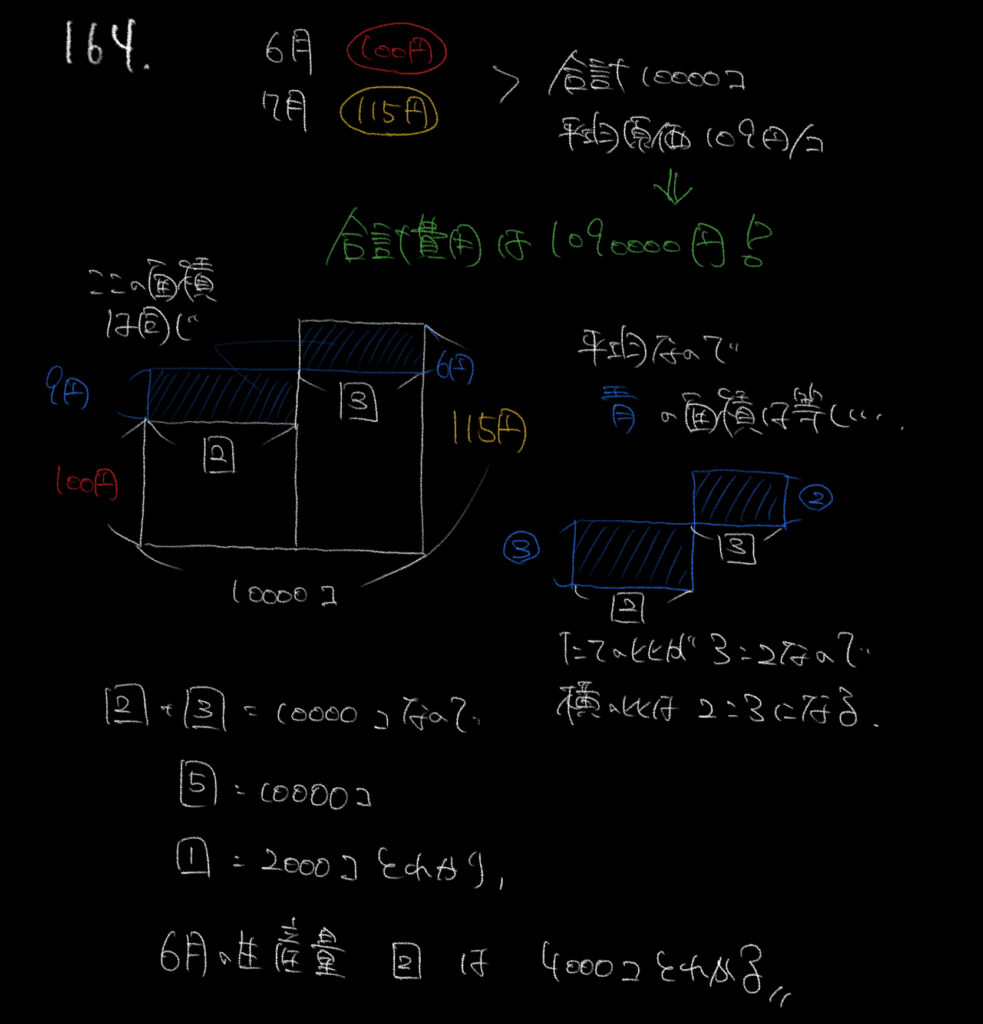

面積図を使った問題でした。
まずは問題文の情報を整理するところから始めていきましょう。
6月は100円、7月は115円で、10000個生産しました。
平均原価が109円ということはトータルでかかった金額は
109円/個×10000個=1090000円になります。
ここから面積図を書いていきましょう。
この考えが今回の問題に使われています。
解説の青の部分の面積が等しいので、ここからさらに逆比の考えを使っていきます。
(詳しく逆比についてやりたい方は下の記事からご覧ください。)
わかっているのは青の部分の縦の比が9円:6円=3:2ということです。
逆比よりここから、横の比が2:3であることがわかります。
□の2と□の3を足した□の5=10000個なので
6月の生産量の□の2は4000個となります。


[165]問題に挑戦!
答えを見るにはここをクリック!
8個
[165]解説を見てみよう!


[163]とほとんど同じような問題でしたね。
まずは全部を1/100倍して問題を簡単にしていきましょう。
すると以下のように問題を書き換えることができます。
次は文章に書かれている条件の言う通りにしましょう。
すると、72円が5枚の食器(8円+12円+16円+18円×2枚)で表せることがわかったので
残りの28円の組み合わせを考えればいいということになります。
この28円の組み合わせは8円が2枚、12円が1枚しか考えられないので3枚とわかり、
もともとの条件で5枚使っているので合計で8枚になります。
[166]問題に挑戦!
答えを見るにはここをクリック!
13年後
[166]解説を見てみよう!


年齢に関する問題でした。
まずは2人の年齢が父と同じになる状況を考えます。
ここでは線分図を使って解いていきます。
年齢の問題で重要になってくるのは、それぞれが取る年齢の割合は同じということです。
5年後にはみんな5歳増えていますよね?
しかし、年齢の合計となるとその話は変わってきます。
父は1年に1歳ずつ歳をとりますが、2人の子供の年齢の合計は1年で2歳分増えます。
この点がこの問題のポイントでした。
よって父親のとる年齢を①とすると、子供達は②であることがわかります。
ここから小学生は線分図、中高大学生は方程式を使って解いていきましょう。
解説ではよりわかりやすく、①、②を使って解いています!
最後に注意ですが、12年後に年齢が同じになるので父を超えるのは12+1=13年後であることを忘れずに!
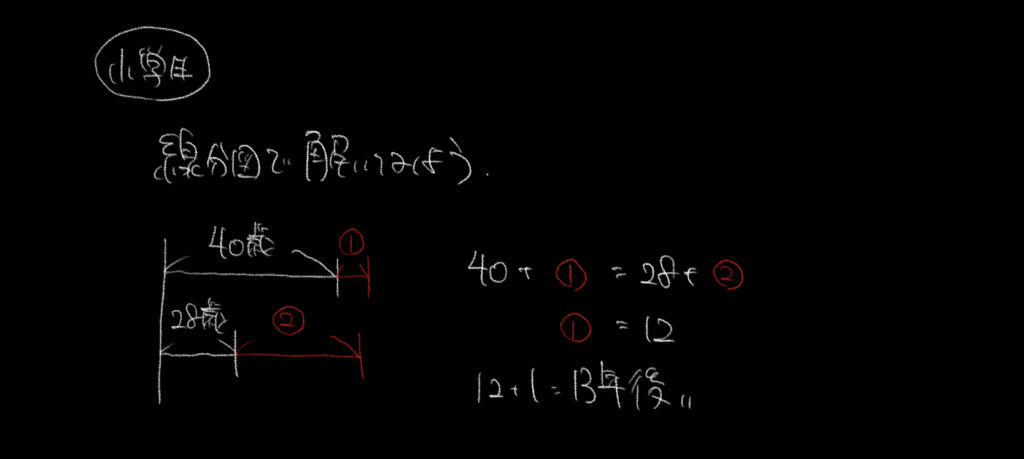
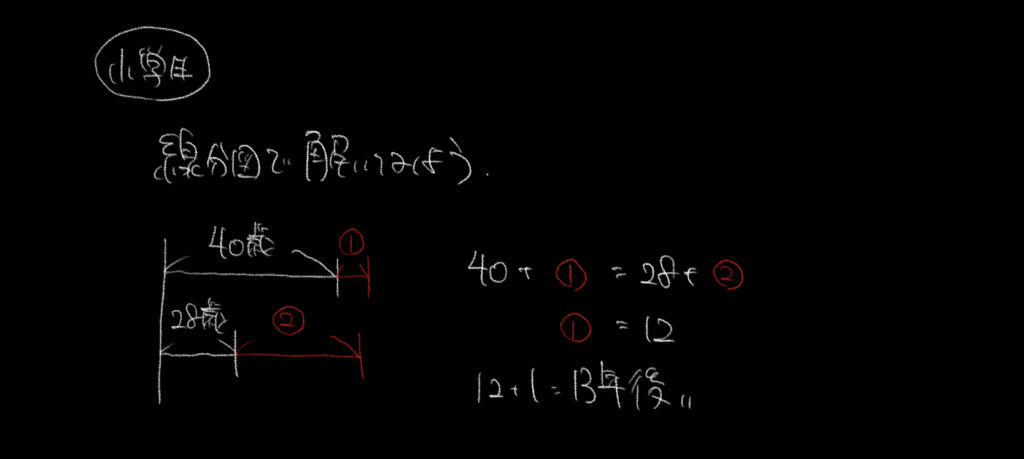


[167]問題に挑戦!
答えを見るにはここをクリック!
40本
[167]解説を見てみよう!
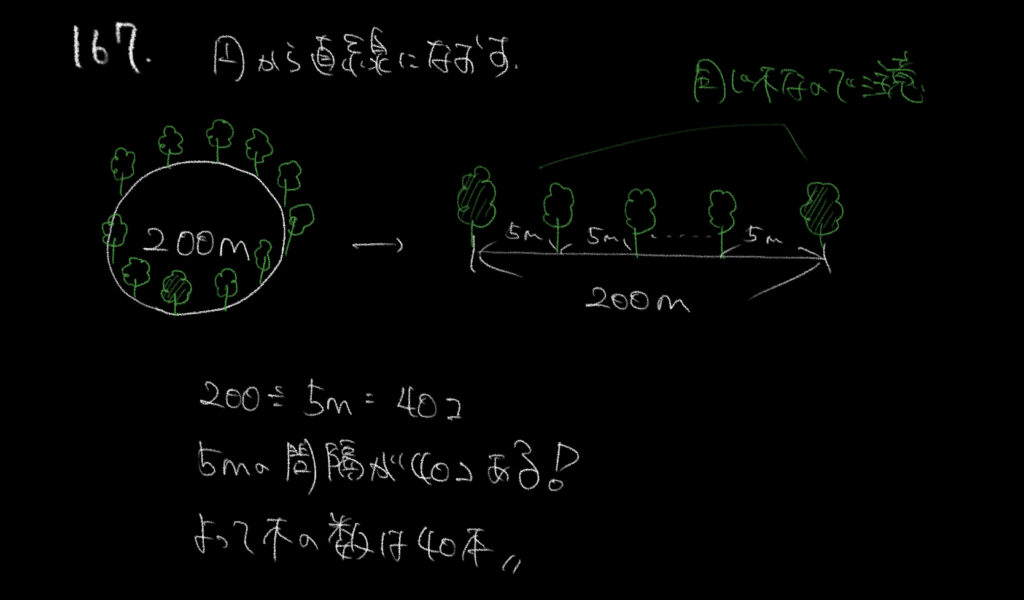

冒頭で触れた植木算です。
それは直線状に木を植えるのではなく、円状に木を植えると言う点です。
これの何が問題かと言うと、円状の木の場合、直線に直すと初めの木と最後の木が同じものになります。
通常ならば、200m÷5m=40個
40個の間隔があるので木の本数は40+1=41本となります。
しかし今回は円状に木を植えるので、初めの木と最後の木は同じ。
よって植える木の本数は40本となります。


[168]問題に挑戦!
答えを見るにはここをクリック!
42人
[168]解説を見てみよう!


条件から人数を推理する問題でした。こちらも「調べと推理」の範囲でした。
この問題の厄介だった点は男性と女性のどちらが多いかがわからなかった点にあります。
しかし心配ご無用。仮定して解いていけばすぐに求まります。
男性と女性の差が9人ということなので、
どちらかの人数を①人とするともう一方を(①−9)人と表すことができます。
ここで男性の人数を(①−9)人と仮定して計算すると途中まではうまくいくものの、
2つ目の計算で人数が小数点になってしまうと思います。
よって男性の人数を①人、女性の人数を(①−9)人として計算します。
IIの条件にも合うように計算すると、男性の人数を42人と求めることができます。
まとめ
特殊算の前半戦はこれで以上になります!!お疲れ様でした〜。
これまでの復習でもあった特殊算の問題はどうだったでしょうか?
万が一よくなかったとしても、きちんと類題や復習をこなせばまだ間に合います。
こまめに貼ったリンクから詳しい解説が読めるのでチェックしてみてくださいね!
特殊算の後半戦では、今までの内容に加え、より複雑な条件問題だったり、
「数の性質」、「規則性」に関わる問題が出てきます。
もう少し一緒に勉強していきましょう!!










