はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います!
今回も今日とて「特殊算」です。
この記事は後半戦ですね。
前回の問題はこちらに置いておきます。


「特殊算」後半戦は「数の性質」、「規則性」が出てきます。
軽く復習してからいきましょう!ファイトです!!
この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
SPI対策:特殊算の考え方



番号は前の記事の続きです!
非言語攻略のカギ⑤:数の性質
数の性質のポイントは以下の通りでした。
約数、公約数
倍数、公倍数
倍数の性質
素因数分解
約数の総和、個数(高校受験の範囲)
2進法
中でも今回大事になってくるのは、倍数、公倍数でした。
とは言ってもそこまで難しくはありません。単語の意味さえ理解していれば解けるはずです。
類題も載せるので、ポイントになる言葉の意味が怪しい方は参考にしてください!


非言語攻略のカギ⑥:規則性
中学受験の規則性の単元では以下の内容が重要でした。
規則を見つける
1年の日数
等差数列、等比数列
中空方陣
入試で大事になってくるのは規則を見つけるの部分です。
しかしSPIでは規則性を見つける問題よりも
複雑なルールに則って問題を解くパターンの方が多いような気がします。
そのような時、問題文は長くなりがちですが、規則にしっかり従えば問題なく解けるはずです。
さて、以上のかるい復習をした上で問題にチャレンジしましょう!!


[169]問題に挑戦!
答えを見るにはここをクリック!
①7個
②20室
[169]解説を見てみよう!


生徒の人数と部屋の数がわかっているので
地道に計算しても答えにたどり着きます。
まずは文章の情報を整理していきましょう!
①6人部屋が22室という時点で、生徒数132人(6人部屋×22室)についてはもう考える必要がありません。
残った生徒は全体の人数の165人から引いて、
165人−132人=33人となります。
使える部屋の数も30室から引いて考えると、
30室−22室=8室となります。
残りの部屋は5人部屋と4人部屋で8室しか使えません。
33人になるように組み合わせを考えると4人部屋が7室、5人部屋が1室となります。



ちなみに面積図を使っても解ける問題でした。余力のある方はチャレンジしてみましょう!
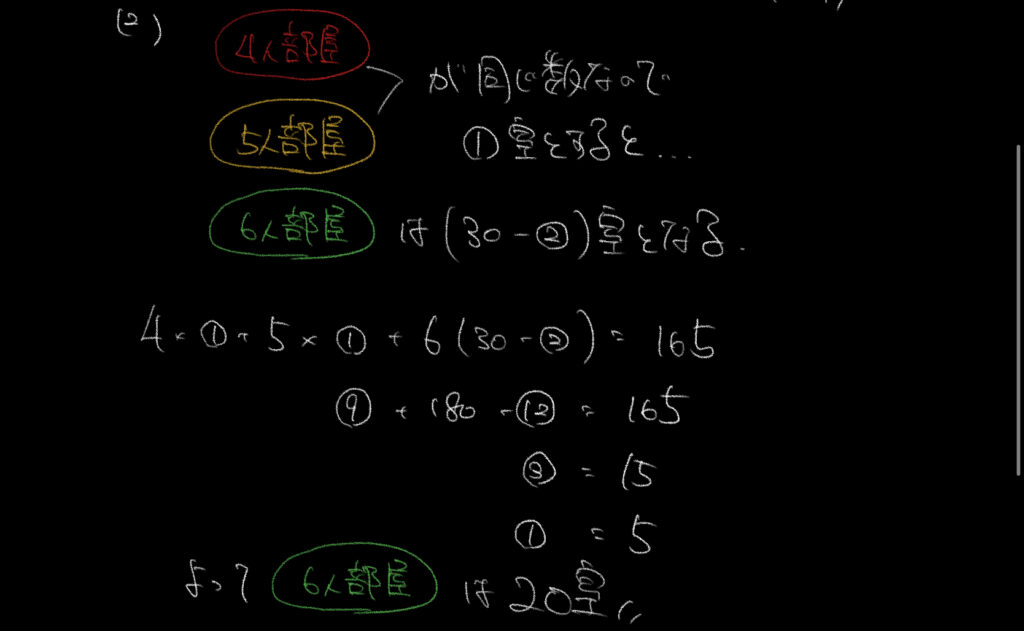
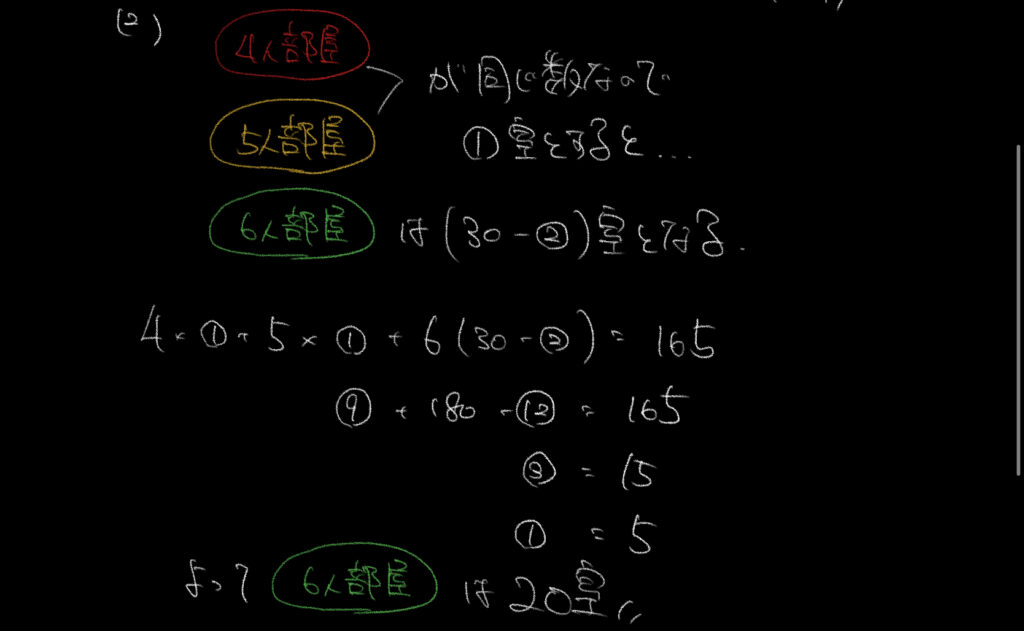
②4人部屋と5人部屋の数が同じなので、それぞれの部屋の数を①室と仮定して考えましょう。
すると、4人部屋、5人部屋の人数をそれぞれ
4人部屋×①室=④人
5人部屋×①室=⑤人と考えることができます。
6人部屋の数は(30−②)室となるので、部屋の人数を
6人部屋×(30−②)=180−○の12となります。
④人+⑤人+180−○の12=165人
全員の人数が165人になるように式を立てると答えを導き出せます!
[170]問題に挑戦!
答えを見るにはここをクリック!
①46枚
②9枚
[170]解説を見てみよう!


①こちらの問題はもう何度もやっている問題ですね!
最低2枚以上買うので、この時点で8枚、計248円分買うことは決まっています。
よって考えるべきところは、
400円−248円=152円をなるべく多く買うにはどうしたらいいかというものです。
多く買いたいので切手は安いものの方が好ましいです。
4円切手ならば、152円÷4円=38枚となります。
なので求めたい数は条件の8枚+38枚=46枚となります。


②最小枚数なので、今度は高い切手から考えていきましょう。
80円切手を5枚買えば、400円になります。
残りの42円は30円切手1枚、4円切手3枚で払えるので合計枚数は
5枚+1枚+3枚=9枚となります!

[171]問題に挑戦!
答えを見るにはここをクリック!
①27枚
②52枚
[171]解説を見てみよう!


「数の性質」に似た問題です。
特にこの下に問題とそっくりですね!
まずは難しく考えずに書き出していきましょう!
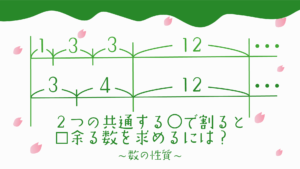

①この条件に当てはまる数を順番に書き出してみると、
17、27、37、47となります。
逆に6枚ずつだと3枚余る数は、
9、15、21、27、33、39、45、51
になります。共通する数は27枚ですね。
このように時間がなくて切羽詰まっていたり、
変な計算をして頭がごちゃごちゃになってるときほどシンプルな書き出しが一番楽なときもあります。
困ったら書き出す練習もしておくといいかもしれません。


②この問題は線分図を使う問題でした。仮定も出てきましたね。
同じところはカードの枚数。人数を①人として線分図を書くと解説のようになると思います。
このとき「余る=線分図に追加される」と「足りない=線分図」から引くことに気をつけましょう。
すると②が12枚とわかるので、①=6枚となり、
カードの枚数の⑧+4枚=52枚
カードが52枚であるとわかります!
[172]問題に挑戦!
答えを見るにはここをクリック!
①820円
②720円
[172]解説を見てみよう!
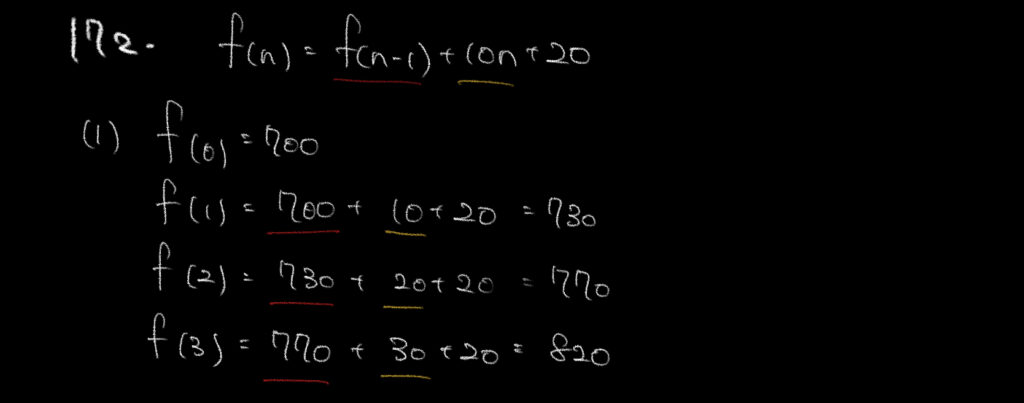
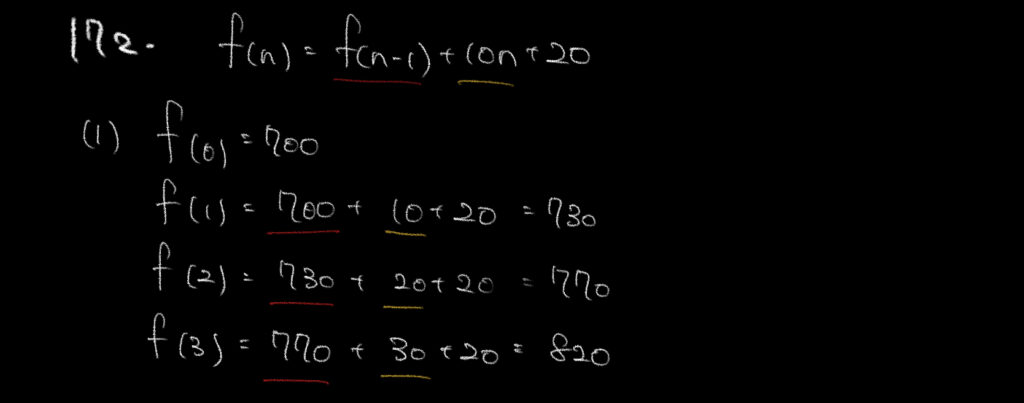
「規則性」のような問題でしたね。
数式が苦手な人は嫌になって飛ばしてしまうかもしれませんが、心配しないでください。
規則が書かれているときはそのまま従えば簡単に解けることができます!
では実際にやっていきましょう。
①n=バイトしてからの年数です。お忘れなく。
始めたばっかりのf(0)=700円だと問題文に書いてありますので、そこから1個ずつ計算していきましょう!
f(n)=f(n-1)+10n+20
f(1)=f(0)+10×1+20なので730円
f(2)=f(1)+10×2+20なので770円
よって3年目のf(3)=f(2)+10×3+20は820円となります。
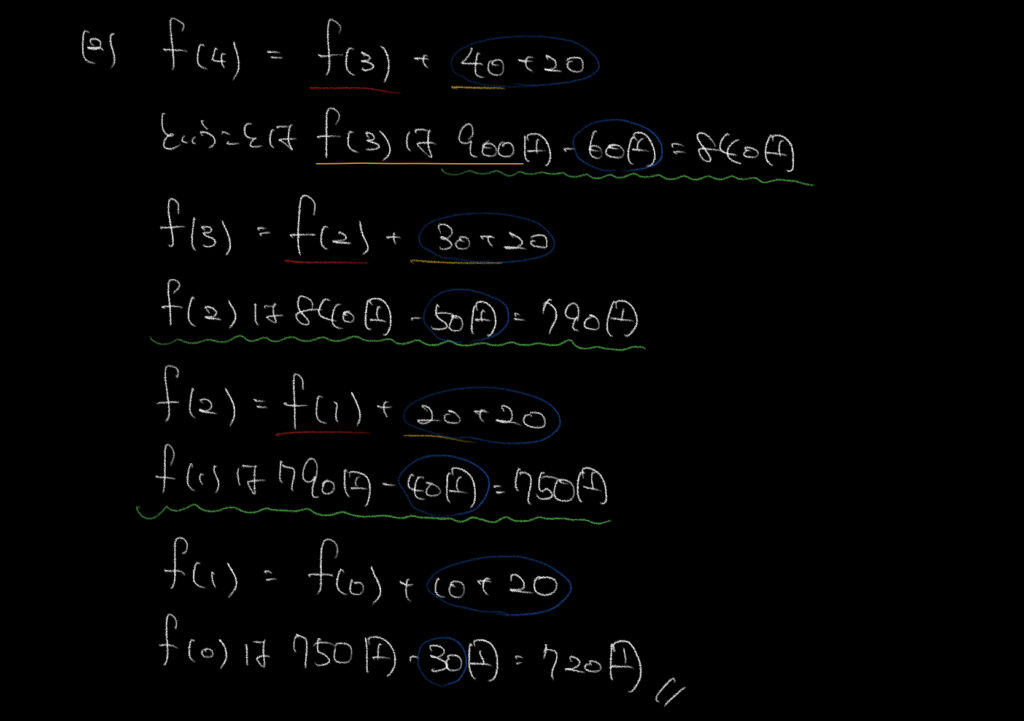
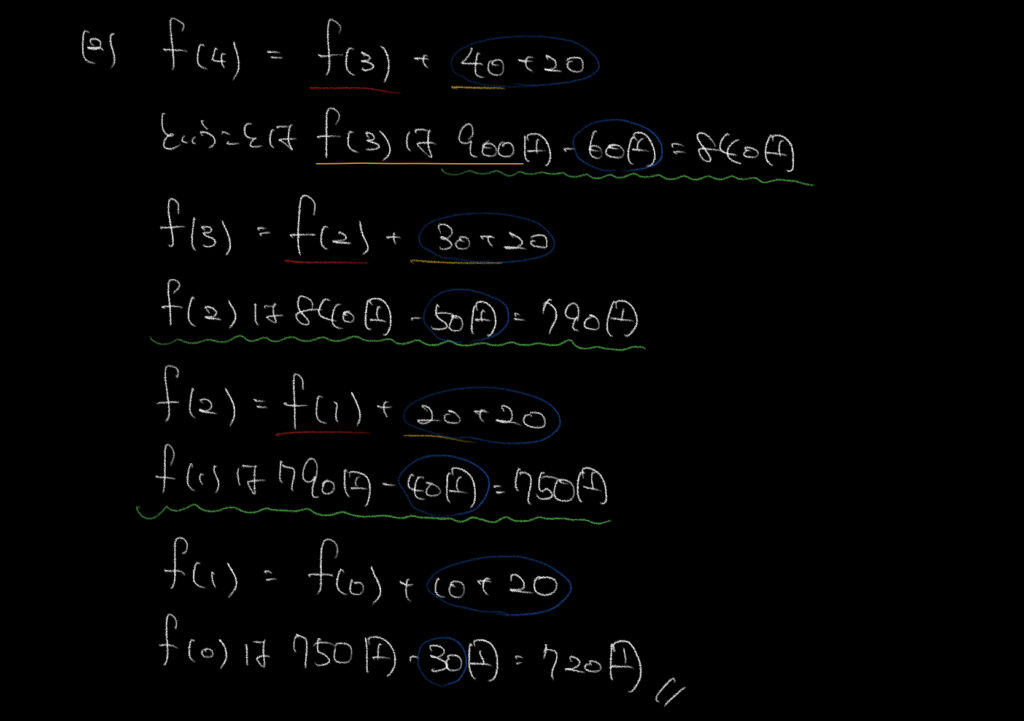
②は①と逆のことをやるだけです!
4年目が900円なので、
f(4)=f(3)+10×4+20=900となります。ここからf(3)=840円となり、
f(3)=f(2)+10×3+20=840円となり、と繰り返していくと
元の金額が720円であったことが求まります。
「規則性」が文章に書かれている類題にも挑戦しましょう↓

まとめ
以上が「特殊算」の問題でした。
しかし、特殊とは言っても難しい内容はそこまでなかったと思います。
ほとんどの問題は今までの復習です。
この記事の問題が苦手ということは、今までの学習に穴があることを意味しています。
もしここで穴に気づけたのなら、早めに修復していきましょう。
早期発見が何よりも大事です!