はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います!
「物の流れ」の問題は正直SPI非言語の問題集でしか見たことがありません。
前回の記事で勉強した「特殊算」よりも、むしろこっちの方が特殊算なんじゃね?とも思いますが、
とにかくやっていきましょう。
ポイントは、問題文で与えられているヒントを書き込みながら図を書くことです!
なお今回の問題は、図が問題文中に与えられています。
このサイトで問題集の問題をそのまま使うことはできないので、図は代替しています。




この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
SPI対策:物の流れの考え方
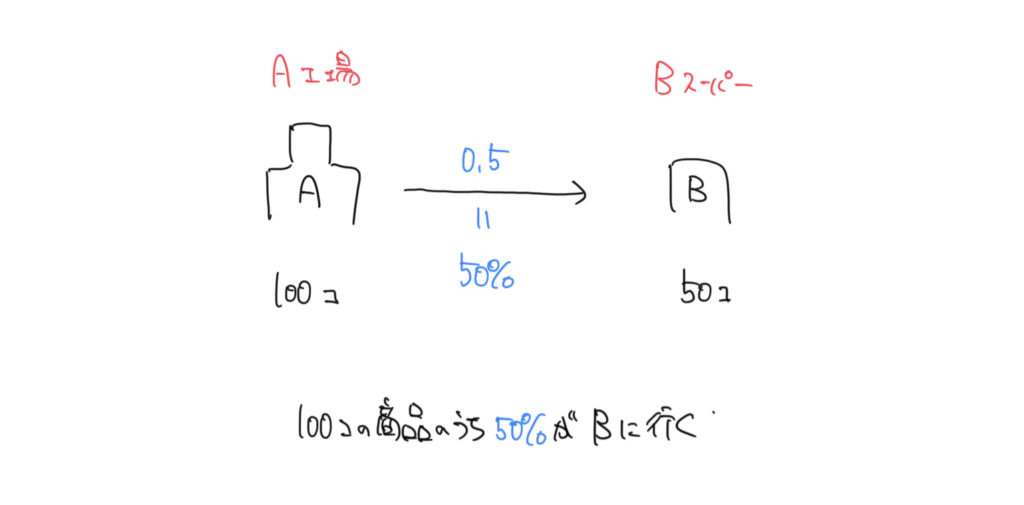

例えばA工場が100個のものを生産したとします。
青で書かれている0.5という数字が、A工場からBスーパーに運ばれる商品の割合です。百分率から0.5=50%とわかっているので、
100個のうちの50%である50個がBスーパーに運び込まれます。
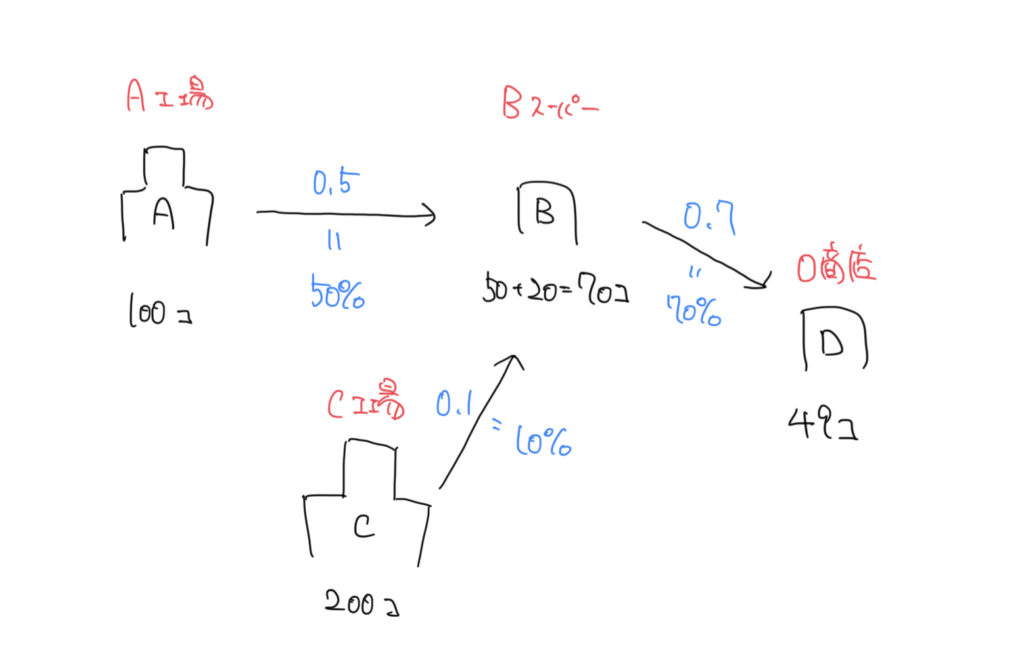

A工場に加えてC工場、D商店があるとします。
AからBにかけては先ほどと同じですが、C工場からもBスーパーへ商品が移動されます。200個のうちの10%なので、20個がBスーパーへ移動します。
合計で運び込まれた個数は20+50=70個です。
さらにそこから、D商店へ70%の商品が移動するので、D商店に運び込まれた商品数は49個と求まります。
ちなみに百分率についての復習はしたから↓


さて、以上を踏まえて物の流れに挑戦していきましょう!!
[175]問題に挑戦!

答えを見るにはここをクリック!
①Q=svK+tvL+uwM
②210%
[175]解説を見てみよう!
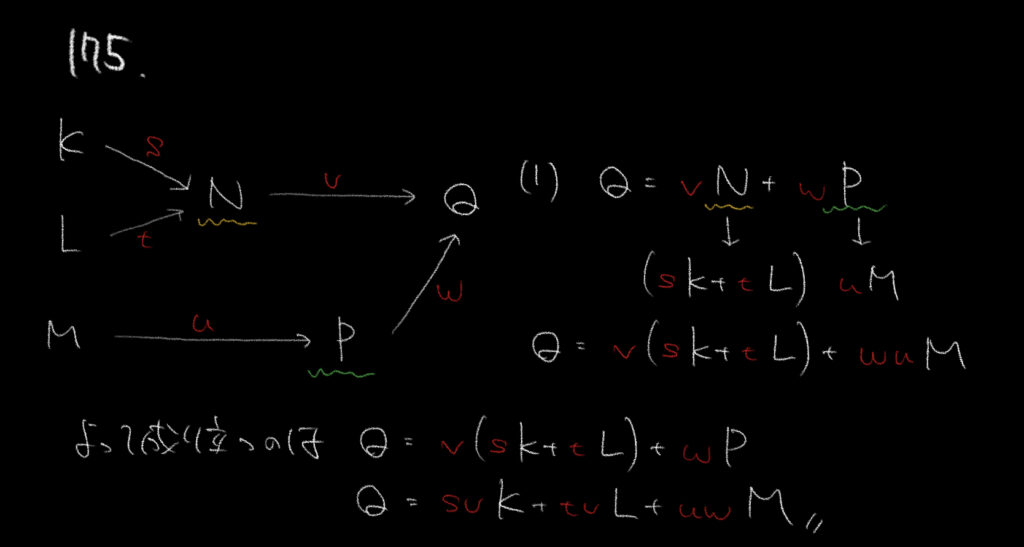
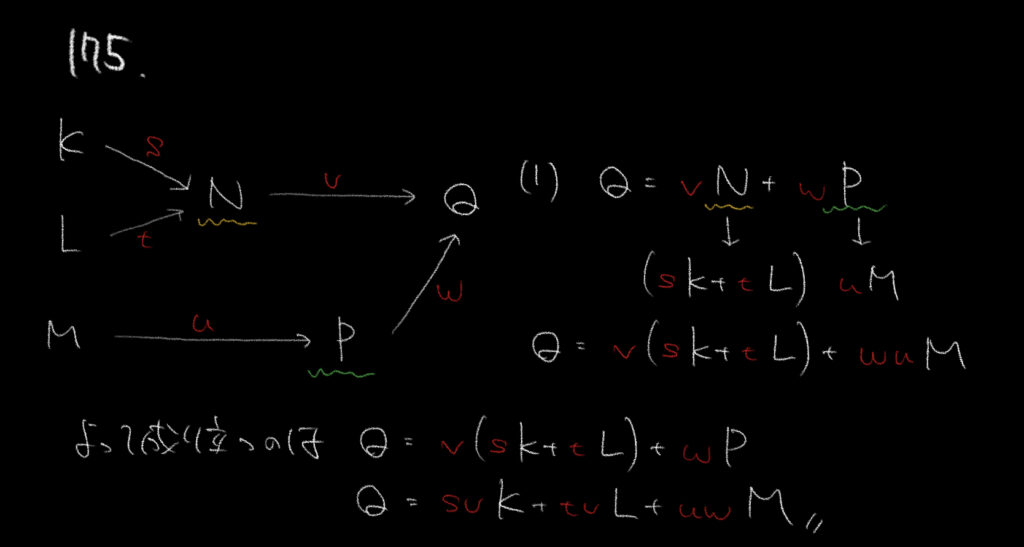
「物の流れ」の問題はとにかく慣れるまで解くのが一番だと思います。
そこまで難しくはないので、頭がこんがらがらないように整理しながら解いていきます。
①選択肢の中から正しいものを選ぶ問題でした。
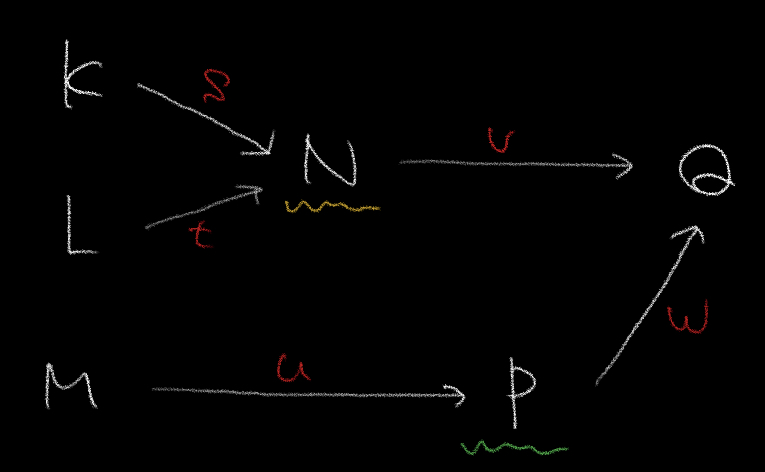
まずはNに注目しましょう。
NはKとLからそれぞれs,tの割合で電気が流れてくるのでN=sK+tLとなります。
またPを同じように考えると、P=uMとなります。
最後のQ=vN+wPと表すことができるので、
これに合うような選択肢を探していきましょう。
一方で矛盾する選択肢を見つけてそれ以外が正しい、という考え方でもOKです!
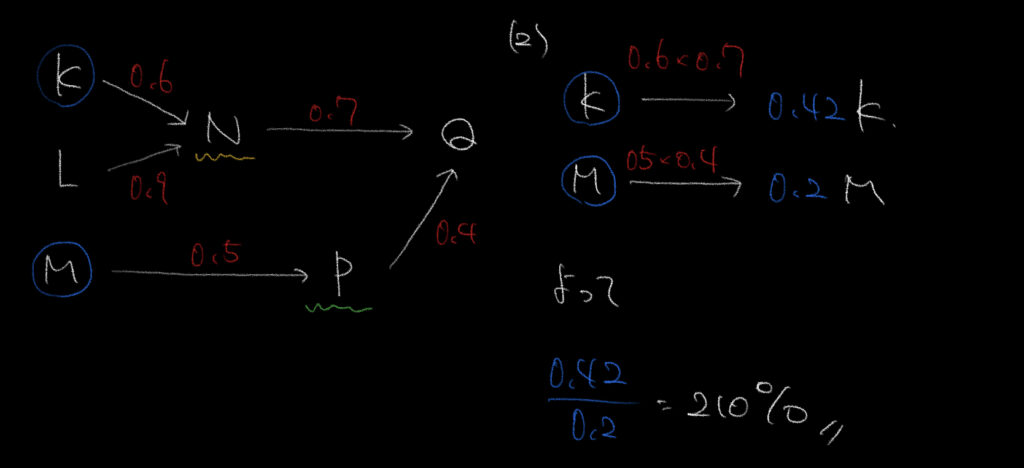

②比率がわかってきたのでまずはそれの書き込みです。
Kの総電気量をKとすると、Qに届く部分は0.42K(0.6×0.7)となります。
同様にMの総電気量をMとするとQに到達するのは0.2M(0.6×0.7)となります。
今回はこの2つの値K,Mが同じと言われているので、
0.42/0.2=210%となります。


[176]問題に挑戦!
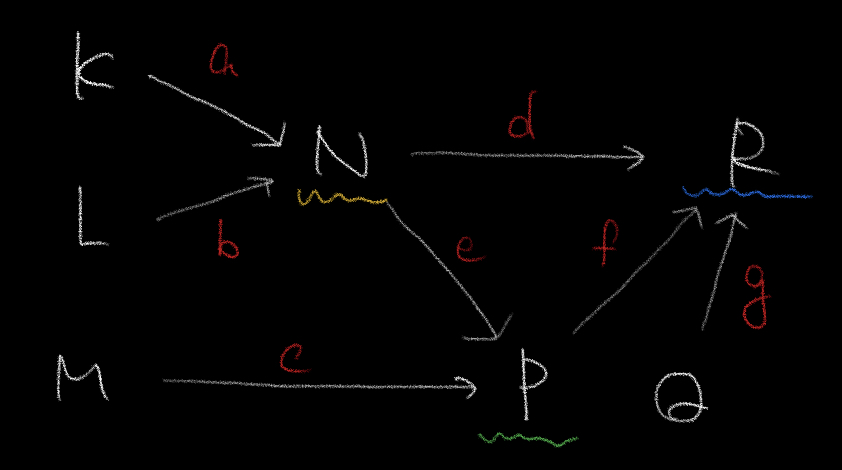

答えを見るにはここをクリック!
①解説参照
②21%
③90人
[176]解説を見てみよう!
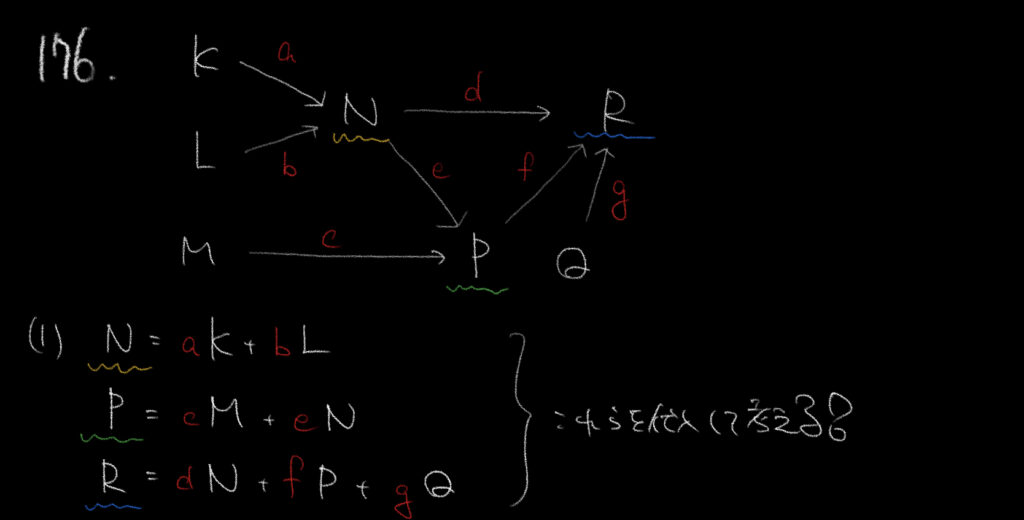

①は先ほど同様選択肢の中から選ぶ問題でした。
しかし少し複雑になっているのでミスのないように考えましょう。
今回特にややこしかったのは、NとPでした。
まずNにはKとLからa,bの比率で人が来ます。
N=aK+bLと表すことができます。
一方でPはNからeの割合で、Mからcの割合で人が移動するので
P=eN+cMとなります。
最後にRについてですが、RはNから直接的に、またPを通じて間接的に人が流れています。
ここに注意して考えるとRに到達するNの割合は、
直接的なものがdN、間接的なものがefNとなります。
これらの点に気をつけて解いていきましょう。
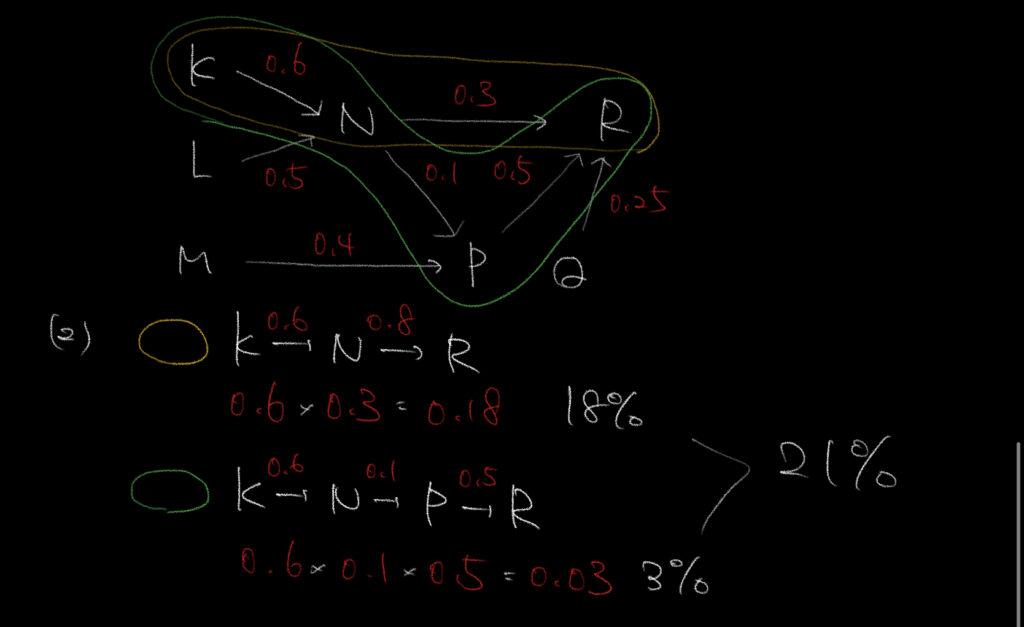

②大会Kの参加者のうち、Rに出場する方法は、
Nへ行き、直接Rに出場するか、Pを通じてRに参加するかの2通りです。
これに気をつけて解いていきます。
まずは黄色のところに注目しましょう。



画像の解説が誤っているので修正します!
誤)N→Rが0.8
正)N→Rが0.3
Kから60%がNへ参加し、さらに30%がRに進むのでKの18%が参加することがわかります。
ここで満足しないでください!!!!
緑の部分に注目してください。
NからPを通じてRに行く人がいるのをお忘れなく!
KからPへ進むのが6%(0.6×0.1)、さらにその半分である50%がRへ行くので、
KからPを通じてRへ移動する人が3%いることがわかります。
よって合計で、18+3=21%とわかります。
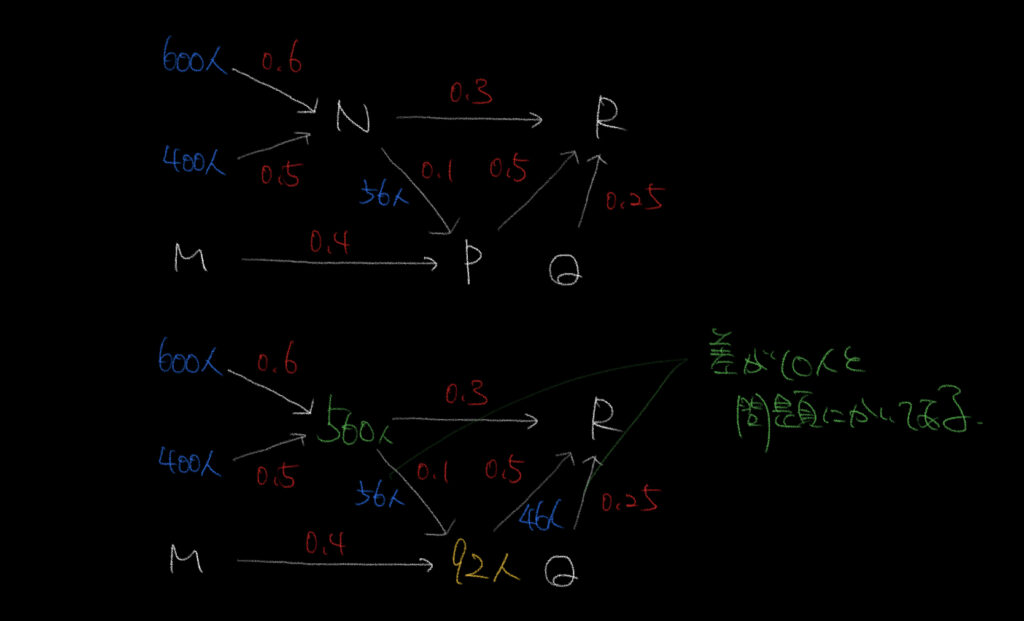

③かなり難しい問題だったと思います。最悪捨ててもいいかもしれません。
大会Nから大会Pに出場した人数は、
大会Pから大会Rに出場した人数より10人多かったという部分がポイントでした。
まずは情報を書き込んでN=560人を求めましょう。
これの10%がPへ向かうのでNから56人が参加することがわかります。
この56人がPからRへ向かう人よりも10人多いので、
PからRへ46人向かったことがわかり、Pには46÷0.5(50%)=92人いた計算になります。
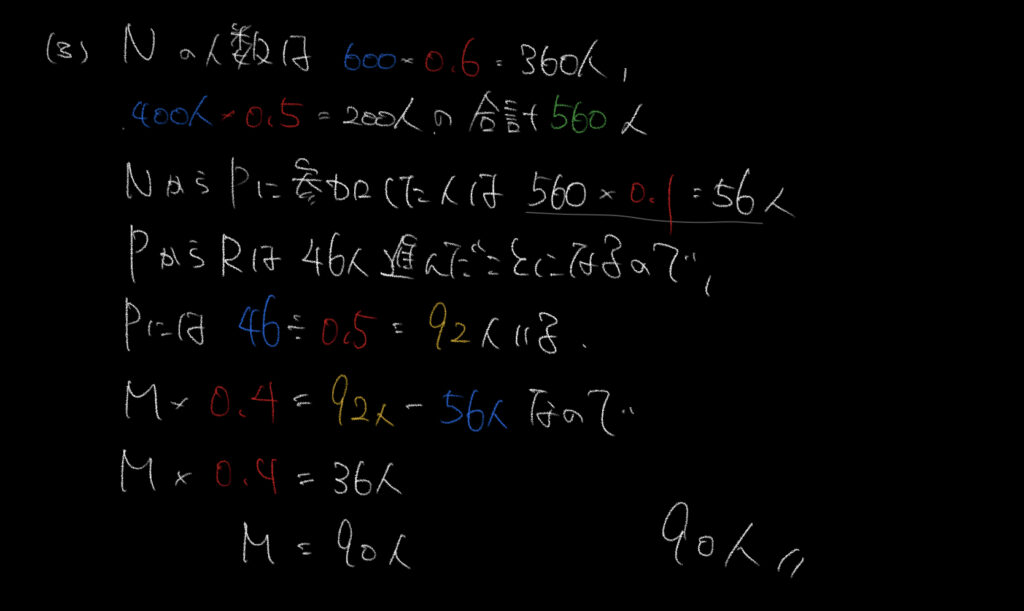
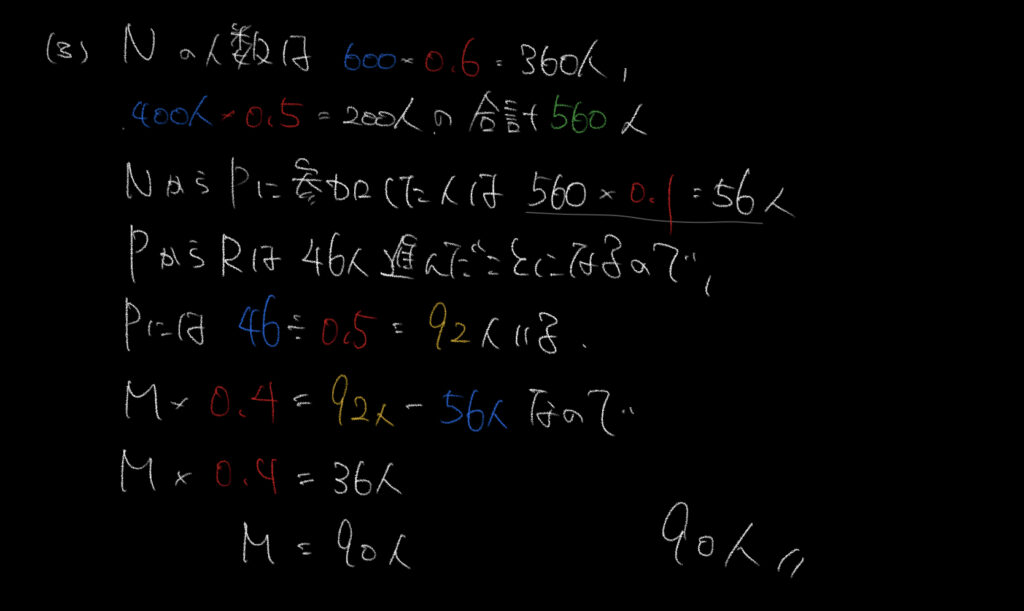
MからPへ移動した人の数は92人−56人=36人となるので、
Mの40%が36人とわかります。
これを逆算して計算すると、36人÷0.4(40%)=90人となります。
まとめ
以上で「物の流れ」は終わりです。
問題数2問と少なめでしたがいかがでしたでしょうか?
コツを掴めば、そこまで難しい問題ではないと思いますが、慣れるまではかなり苦労するかもしれません。
百分率についての復習を忘れずに、頑張ってみましょう!











