はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です!
今日は中学受験算数の攻略法「面積図」について勉強していきましょう!
面積図の書き方はいくつかの記事でも書きましたが、
ここでは超基本である面積図の書き方の説明から、
実際の問題で使われる発展した形まで解説していこうと思います。
例題も多数用意してあるのでぜひ覚えるようにしてください!
「さんすうがく」で使われる解説のほとんどは面積図や線分図なので、理解度も大幅に上がります!
それではやっていきましょう!
この記事では面積図に重きを置いて解説しているので、面積図に付随する解法などは省略して説明している場合があります。丁寧な解説をお求めの方にはリンクを挿入していますのでそちらでご覧ください!
この記事を書いている人はこんな人


面積図の書き方
具体的な書き方は以下の通りです。
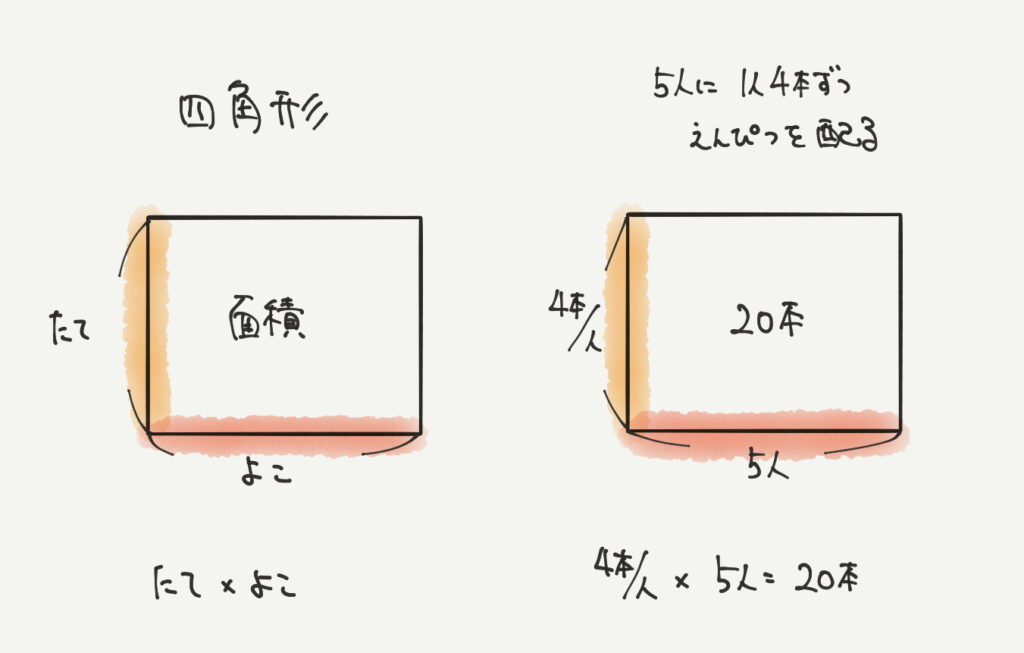

「四角形の面積の求め方=たて×横」を使うとこのように鉛筆の本数を求めることができます!
4本/人×5人=25本となりますね!
これらのように四角形の面積を求めるように数字を入れていきましょう!
ここで注意して欲しいのことがいくつかあるので説明します。まずは面積図の書き方です。
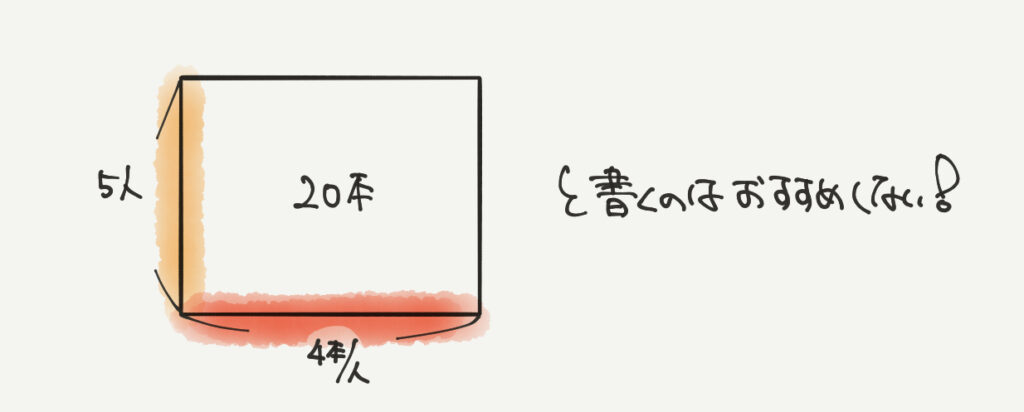

たてを5人、横を単位量あたりの数(4本/人)とやるのはおすすめしません。
単純にたてと横を反対にして計算してしまうと解きづらいからです。
ちなみに単位量あたりの数は下の図のように表すことができます。
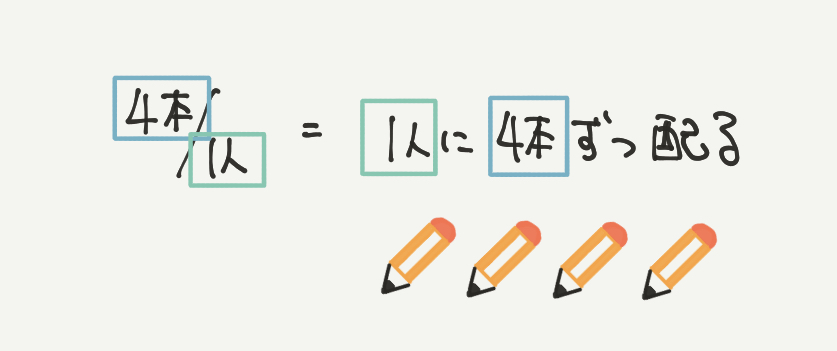

よくわからない単位がててくると混乱してしまいますが、成り立ちを理解すれば簡単です!
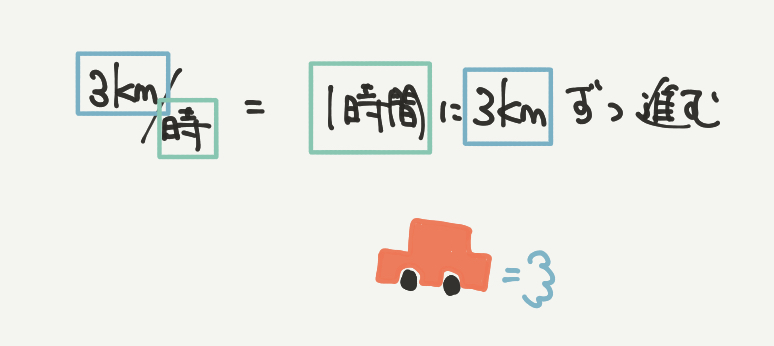

ちなみに、車の速さなどで使われる時速や分速も単位量あたりの数です。



ここまで大丈夫でしょうか?
面積図の書き方に注意した後は単位に気をつけましょう。
これを間違えてしまうと面積図で解くことができません。
どういうことかというと、例えば時速3kmで6km進んだ人の走った時間を求めるとき、
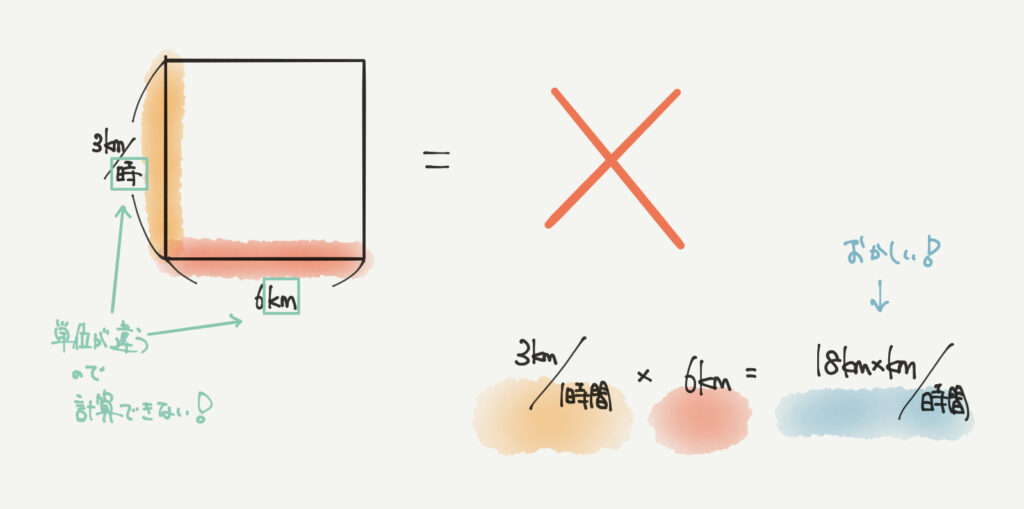

と、計算してはいけません!!
この面積図からもわかると思いますが、単位をそろえないと面積が出せなくなってしまいます。
こうならないために、数字それぞれの単位をしっかりと確認していきましょう。
ちなみに正解はこちら↓
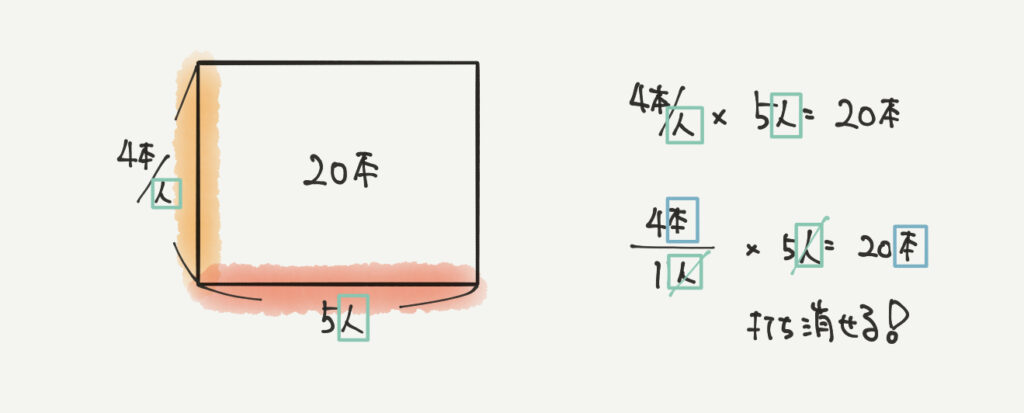

数字だけ書くのは絶対にダメです!!!そこだけは必ず守ってください!
面積図の書き方を徹底解説!6つの例題に挑戦!
それでは試しに面積図を書いていきましょう。
答えを見るにはここをクリック!
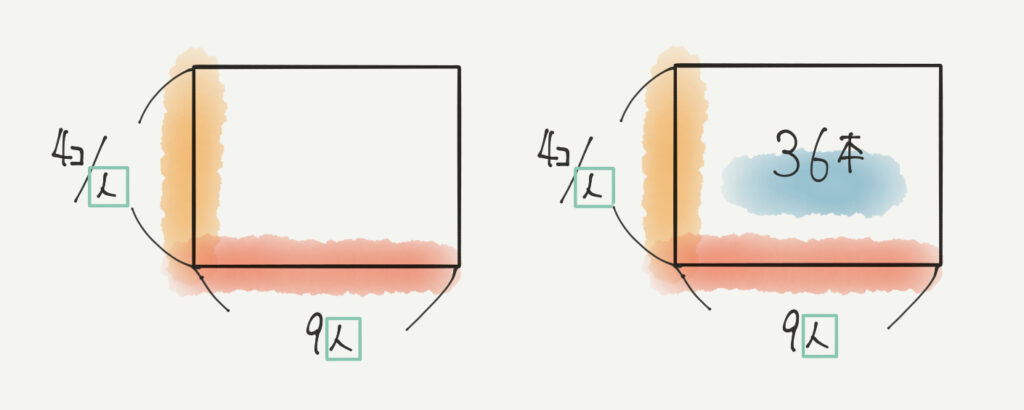

一人4個ずつで、9人に配るので全部で36個になります。
答えを見るにはここをクリック!
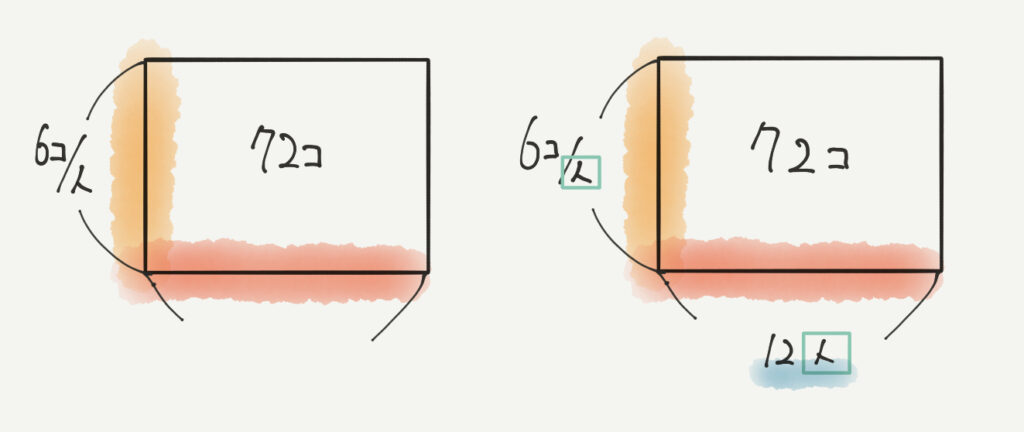

今度は逆に一人に6個ずつ配ったら72個配れた、というパターンです。よって72個÷6個/人=12人です。
答えを見るにはここをクリック!
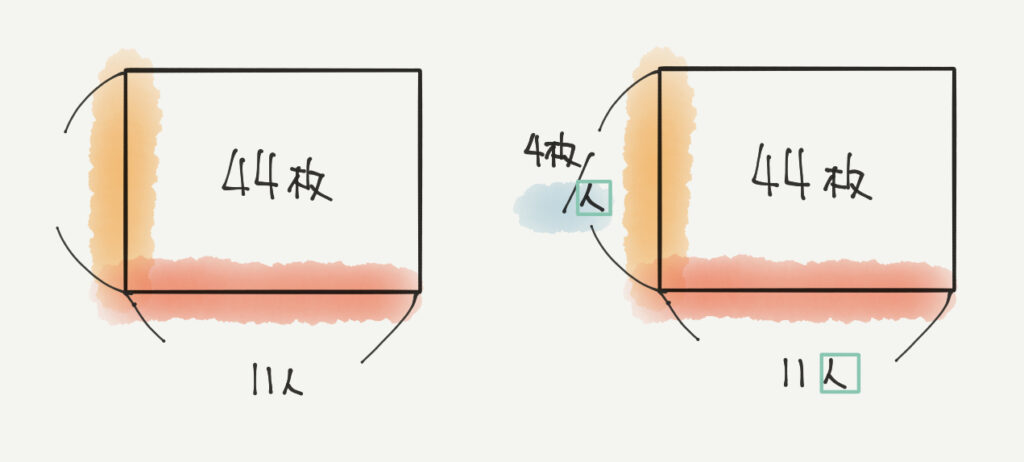

こちらも似た問題で、全体数と配った人数がわかっているので、44枚÷11人=4枚/人となります!
答えを見るにはここをクリック!
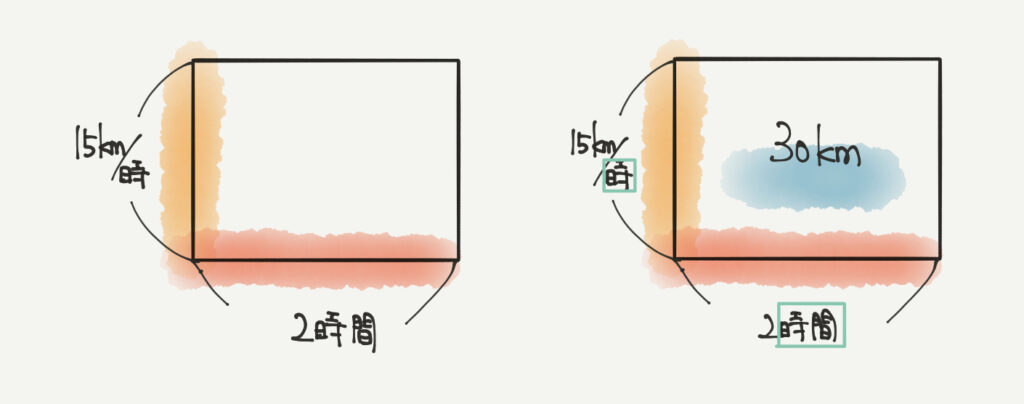

速さの問題は特に「時間」「分」「秒」の単位がありますので気をつけるようにしてください。
詳しくは後程の問題で解説します。
答えを見るにはここをクリック!
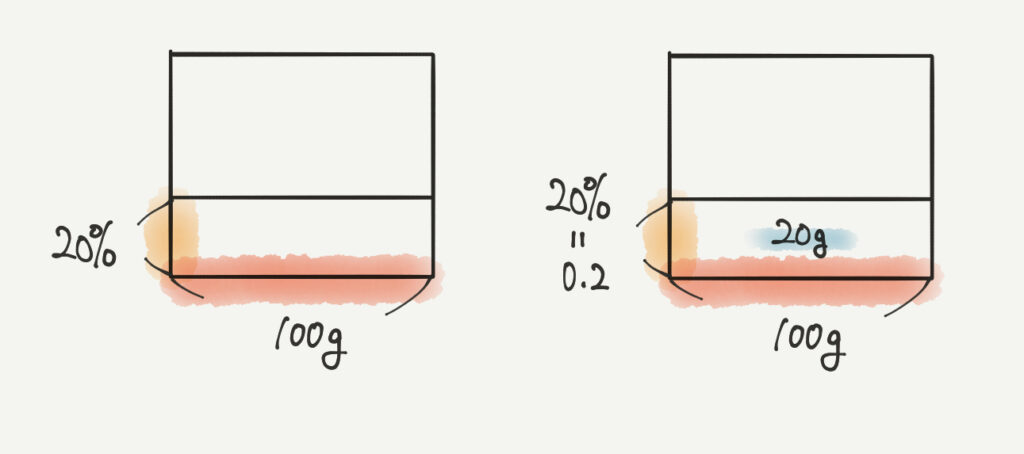

こちらの問題は百分率が含まれる問題でした。簡単におさらいしましょう。
百分率は割合をパーセント%の形で表したものになります。
100%を1と表します。今回は20%なので0.2と表されます。


答えを見るにはここをクリック!
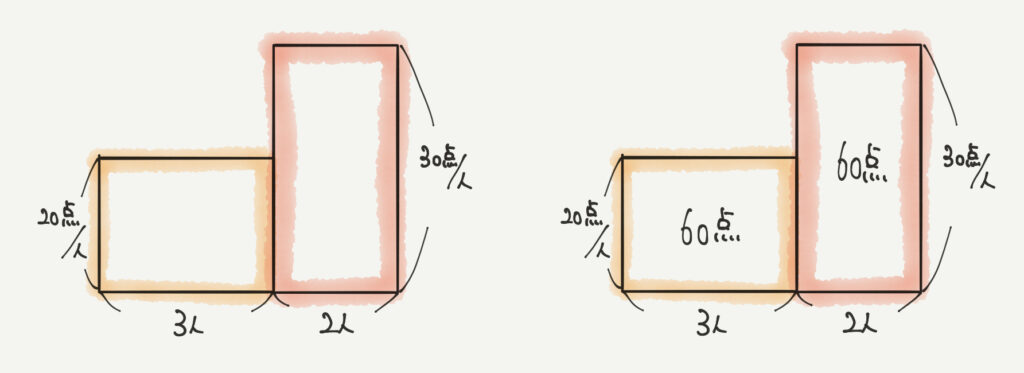

黄色の部分、赤の部分で面積を求めていきましょう。
- 20点/人×3人=60点
- 30点/人×2人=60点、となるので、60点+60点=120点となります。



さて、ここまでが面積図の基礎中の基礎でした。
ここから食塩水、速さ、平均などの問題に取り掛かりましょう!!
面積図攻略のカギ①:平均を理解せよ!
さてまず初めに平均です。面積図を用いて同じところを見つけながら解いていきましょう!!
平均の考え方です。それでは解いていきましょう。


答えを見るにはここをクリック!
解答:65点
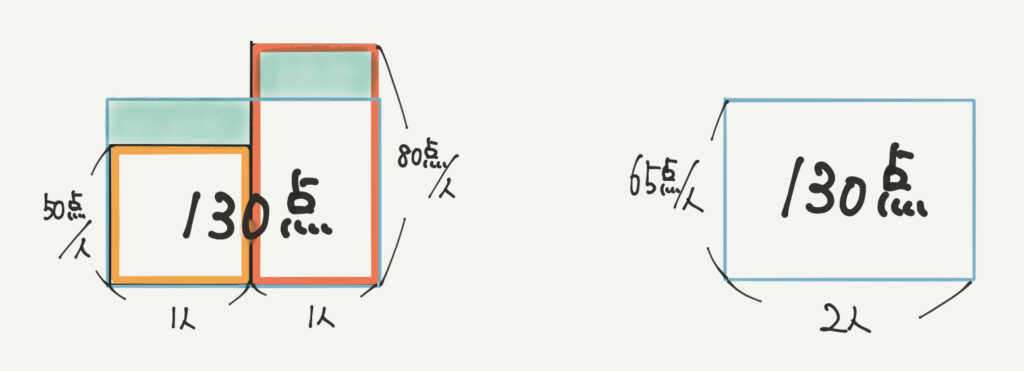

それぞれ50点、80点取っているので2人で130点とったことになります。
よって青の面積図に130点、2人と書き込めます。
これにより130点÷2人=65点/人と計算して求めることができます。
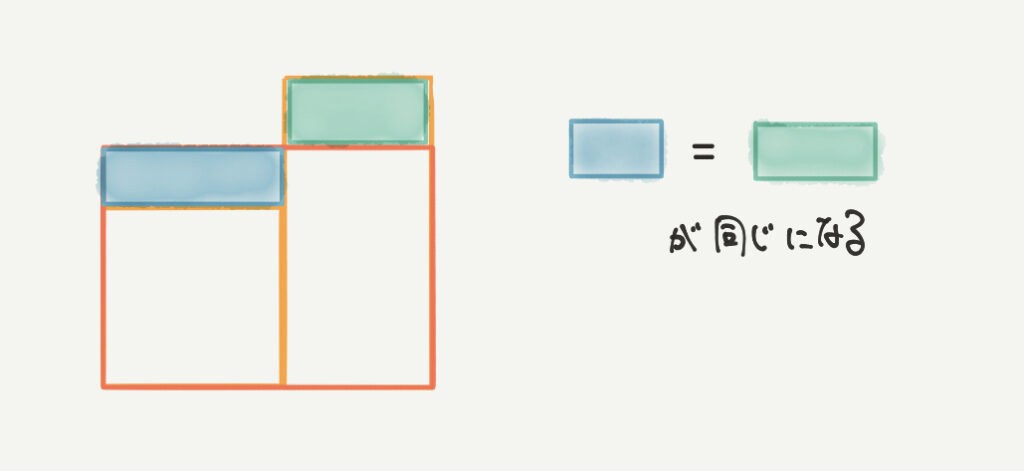
ちなみにこのとき、移動した緑の部分の面積は同じになります。
後の問題でこれを使うのでよく覚えておいてください。

答えを見るにはここをクリック!
解答:295cm
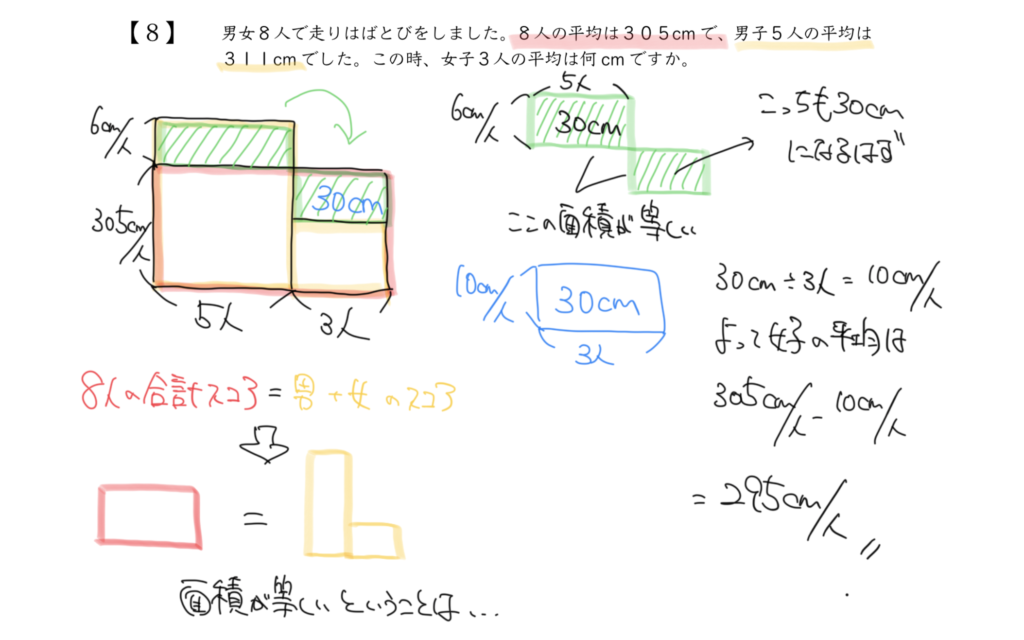

男子と女子の比を使った面積図になります。黄色の面積の合計と赤が等しくなるので緑の面積が等しくなります。
片方の面積は横が5人、たてが6cm/人と決まっているので30cmとわかります。
同様に考えると青の部分の面積も30cm、人数は3人なのでたては10cm/人です。
後は平均の305cmから10cmを引きましょう。
男子は5人、女子は3人なので人数比は5:3となり、逆比の考えを使っても解けます。


答えを見るにはここをクリック!
解答:3:5
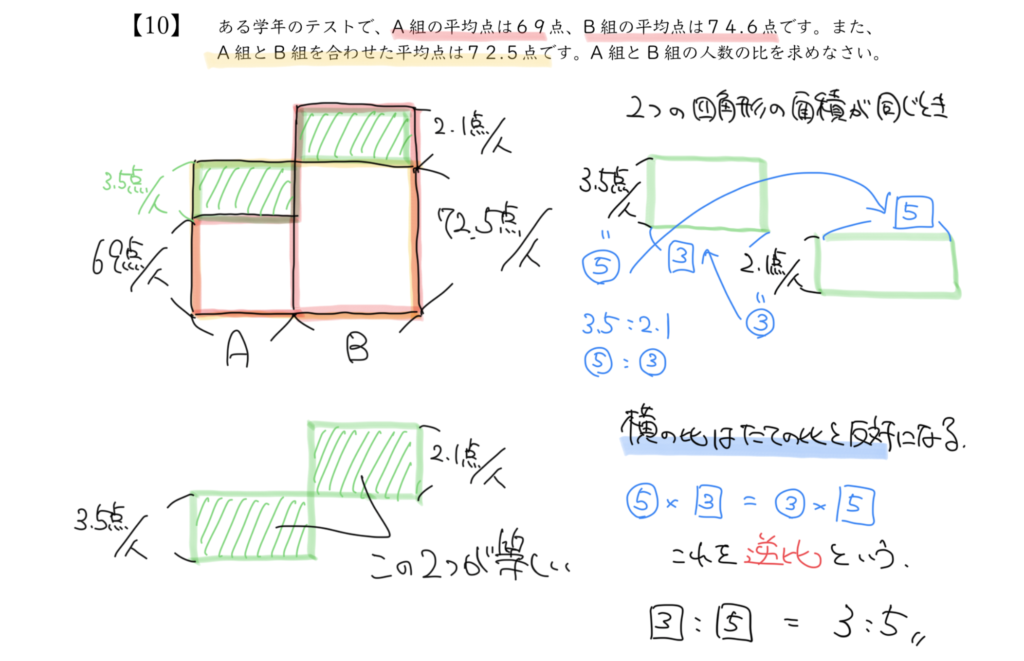

逆比と面積図の問題でした。
平均の考えを使うと緑の部分の面積がおなじであると気づきますね。
面積が同じでたての長さが3:5なので横の比は5:3となります。
面積図を書くことで逆比についてのイメージがしやすかったと思いますがいかがでしょうか。
実際に計算のみでやってしまうと解けなくなる人もいると思います。
面積図の重要性がわかる一問でしたね。

面積図攻略のカギ②:食塩水を攻略せよ!
食塩水の問題も面積図を使って解いていきましょう。
まずは簡単な問題から!
答えを見るにはここをクリック!
解答:20g
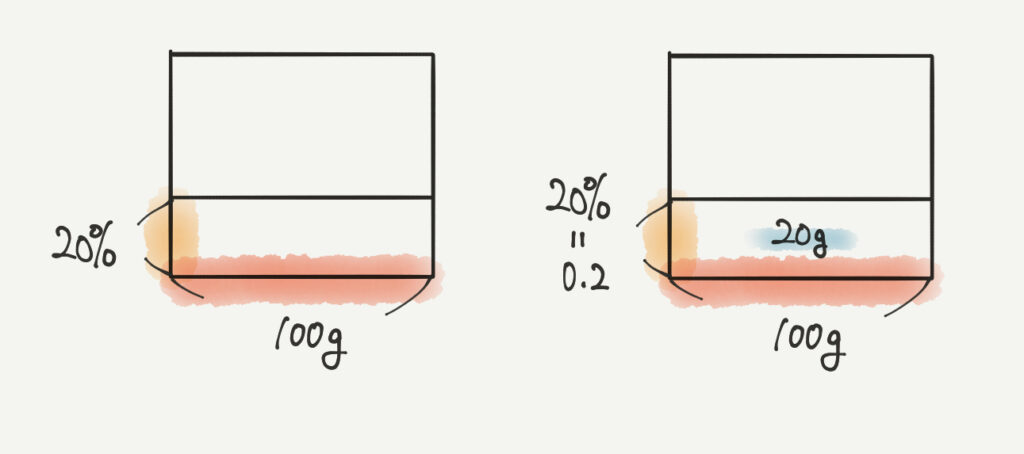

面積図に当てはまる数を入れていきましょう。
今回は%の値と塩の量がわかると思います。
四角形の面積はたて×横なので、全体量×%=塩の量になるはずです。
よって100g×0.2 (20%)=20gとなり、食塩=20gと求まります!
答えを見るにはここをクリック!
解答:190g
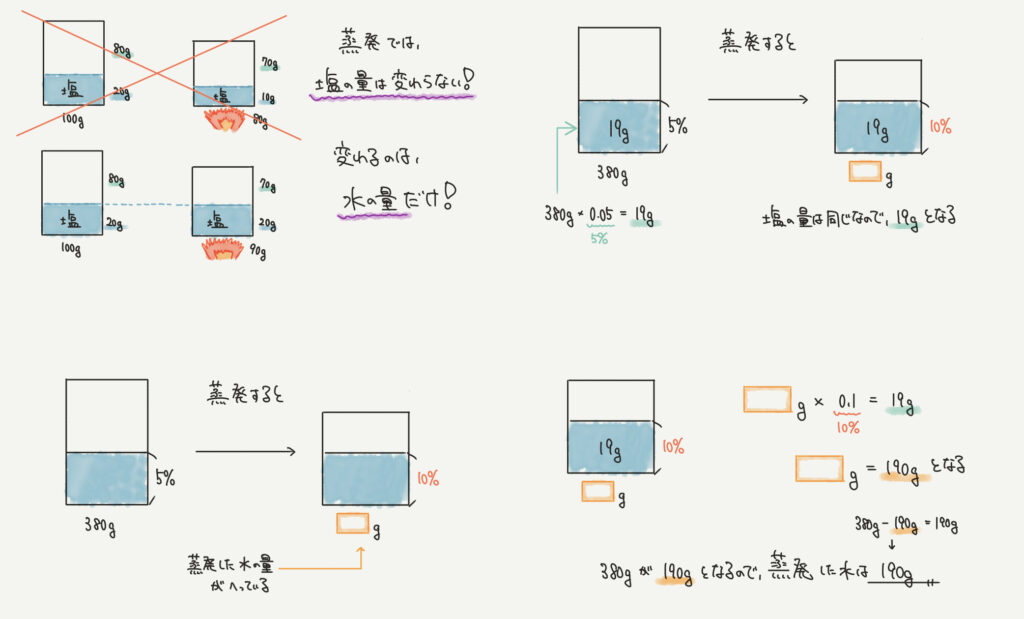

面積図に当てはまる数を入れていきましょう。
今回は%の値と塩の量がわかると思います。
四角形の面積はたて×横なので、全体量×%=塩の量になるはずです。
よって100g×0.2 (20%)=20gとなり、食塩=20gと求まります!
先ほどより少し難易度の高い問題でした。
ポイントとなるのは塩の量。蒸発は水が減るだけなので塩の量は変わりません。
よって塩の量19gは変化なしです。
これを踏まえて図を書いていくと19g、10%という情報を書き込むことができます。
10%は小数で表すと0.1なので、食塩水の量は190g。
つまり水は380gから190gへ190g減ったことになります!
詳しい解説はこちらからご覧ください!


答えを見るにはここをクリック!
解答:13%
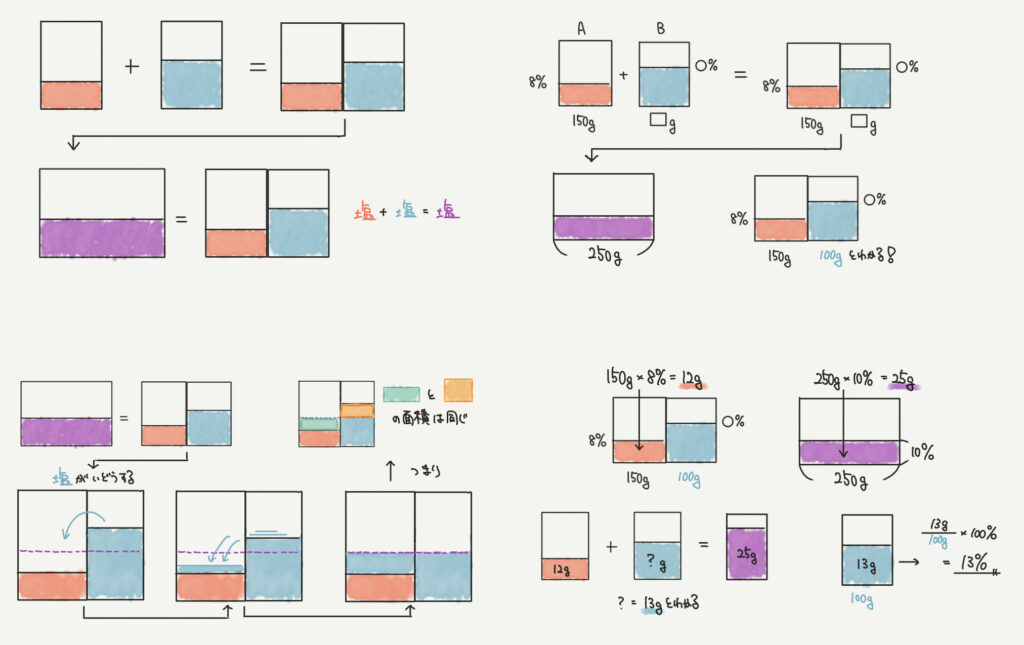

難しい問題になればなるほど、面積図以外の要素(百分率や逆比)などの考えを使わなければいけません。
単元別だけで解いてしまうと横断的な考えができず、決まった解き方になりがちなので注意してください!
今回分かっているのがAの塩の量です。
Bの食塩水の量は混ぜた合計が250gと分かっているので100gと求まります。
平均の考えを使うと青の部分が同じ面積であるとわかるので逆比を用いて解いていきましょう。
詳しい解説はこちらからご覧ください!


面積図攻略のカギ③:速さの問題で書く面積図は「単位」に注意せよ!!
速さの問題は特に単位に注意することが大事でしたね!
こちらも3段階でやっていきましょう。
答えを見るにはここをクリック!
解答:9時間
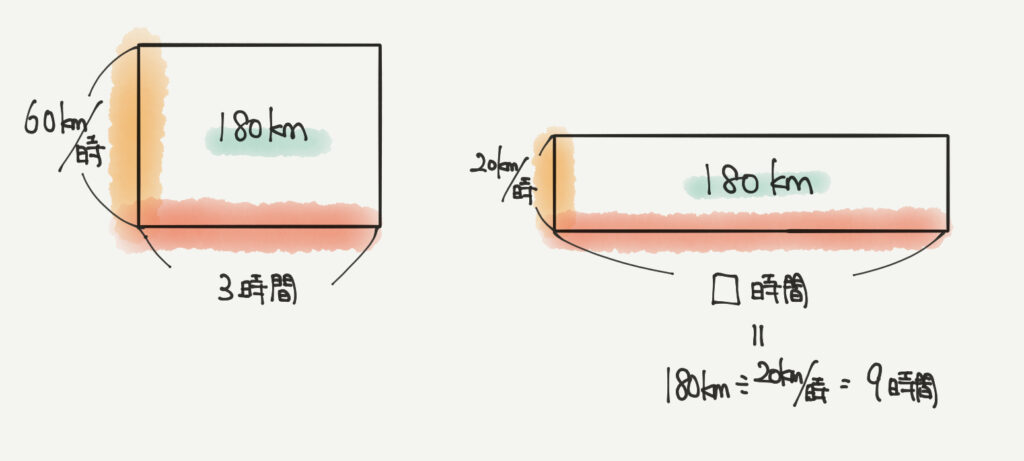

まずは時速60kmで3時間進んだ距離を求めましょう。
60km/時×3時間=180kmとなります。
これを時速20kmで進むので180km進むには
180km÷20km/時=9時間となります。


答えを見るにはここをクリック!
解答:8km/時
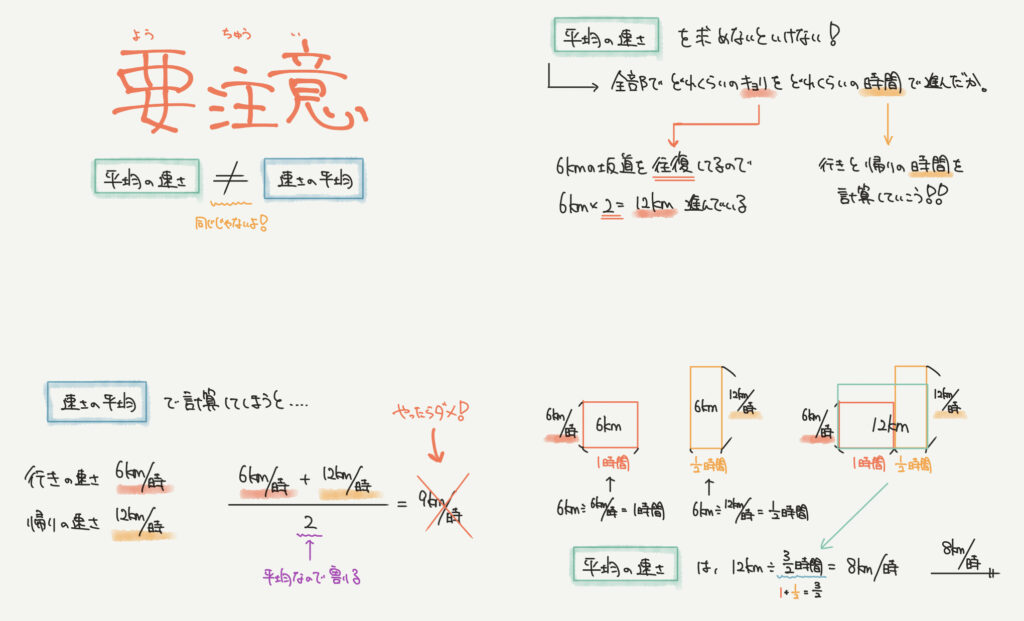

行きも帰りも進んだ距離は同じで、時速が違う問題でした。
なのでそれぞれかかった時間を求めていきましょう。
6km÷6km/時=1時間
6km÷12km/時=1/2時間となります。
合計12kmの距離を3/2時間で進んだことが面積図から分かりますので、
12km÷2/3時間=8km/時
単位を揃えることに気をつけましょう。
かかった時間と距離の合計が分かっているので平均を求めることができます。

答えを見るにはここをクリック!
解答:40分
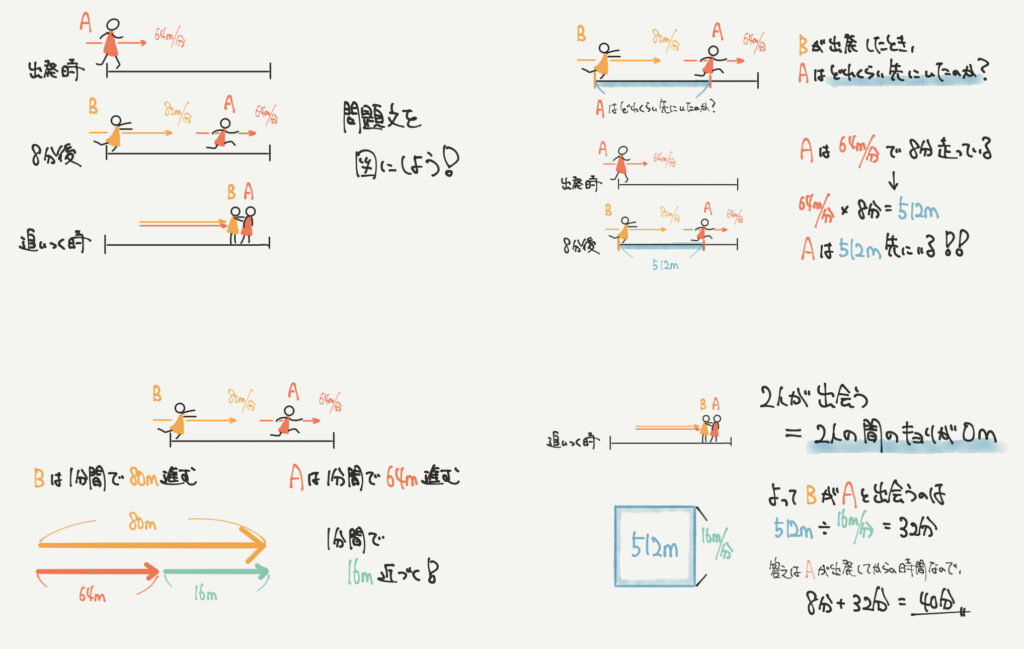

少し線分図が出てきます!!
BくんがAくんを追いかけたときのAくんの進んだ距離に注目しましょう。
Aくんは8分間進むので面積図を使って進んだ距離が512mとわかります。
ここからBくんが追い上げるので1分で16m近づきます。
これも面積図を使って求めていくと40分と求めることができます。


面積図攻略のカギ④:仕事算も面積図!ポイントは仮定すること!
まず仕事算のちょろっとした復習です!
仕事算では仕事量を仮定すると、わかりやすく問題が解けます!
ここで重要なのは全体の仕事量をいくつと仮定するか、です。
答えを見るにはここをクリック!
解答:20日
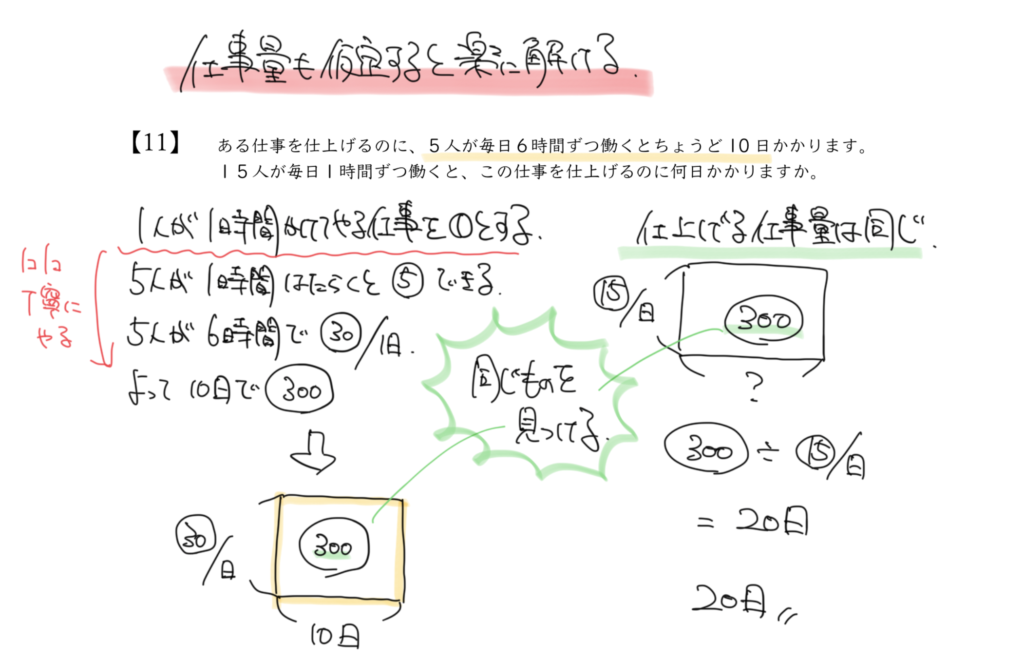

仕事算の典型問題です。仕事の量を5と6、10の公倍数である300と仮定します。
すると、15人で1時間ずつ働くと300÷⑮/日=20日と求まります。
仕事算では1人が1時間でやる仕事を①と仮定することが大事でした。
ただ、これはすべての問題に共通するわけではありません。
きちんと文章を読んで何を仮定するのかを考えましょう。




答えを見るにはここをクリック!
解答:10日
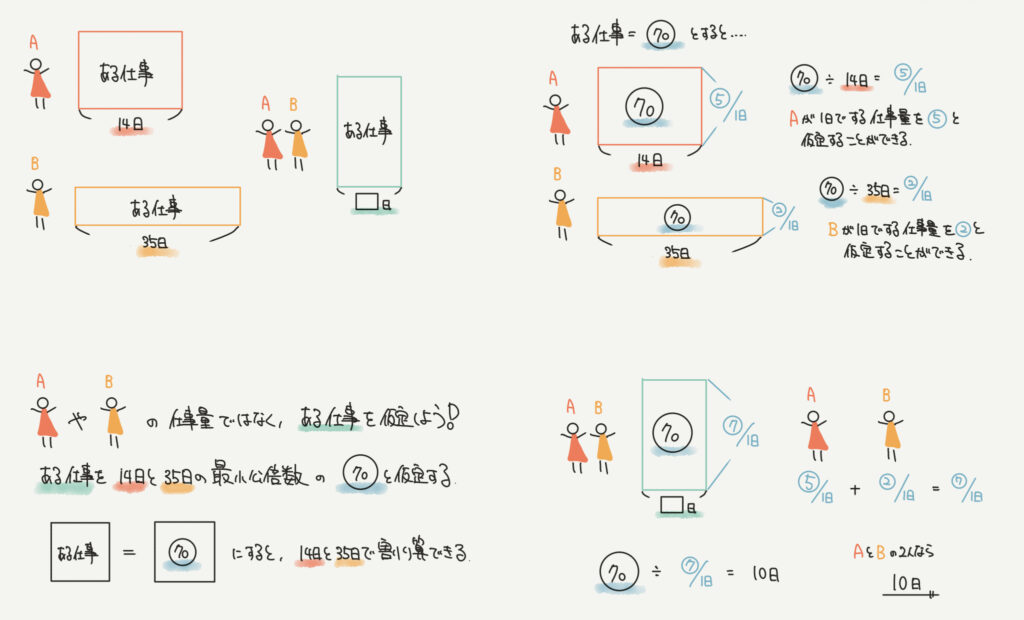

仕事量を仮定して解いていきましょう。
14日と35日が出てきてるので最小公倍数の70を仕事量と仮定します。
すると14日かかってAは仕事をするので⑤/日、Bは35日で終えるので②/日となります。
ここから合計の仕事の割合が⑦/日となり、答えが10日となります。
詳しい解説はこちらからご確認ください!


答えを見るにはここをクリック!
解答:10日
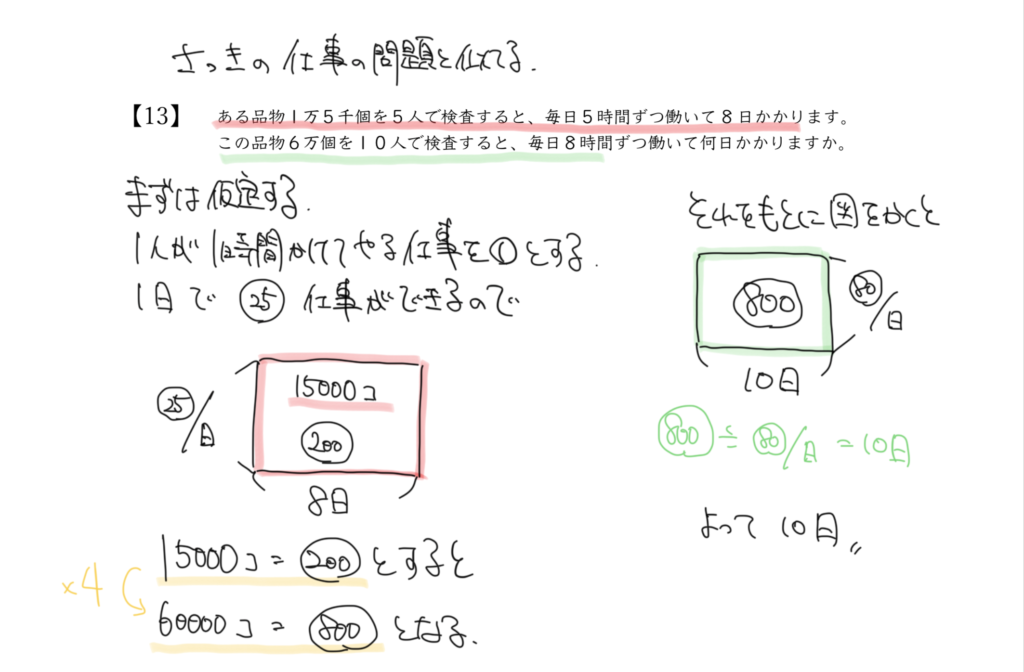

多少難しくなっても考えることは同じです。
仮定して面積図を書きましょう。
5人で1日5時間なので、㉕/日となります。
この割合で8日かけて仕事を行うので○の200と求められます。
これが1万5千個なので、そこから○の800を求めましょう。
すると○の800=6万個と計算できます。
800とわかれば後は1日あたりの仕事量で割るだけです。
○の800÷○の80=10日となります。


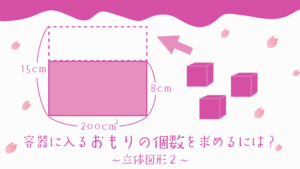
面積図攻略のカギ⑤:立体図形の問題も面積図で攻略!?
答えを見るにはここをクリック!
解答:12箱


つるかめ算と呼ばれるタイプの問題でした。
それぞれの単位量あたりの数と箱の数を面積図に入れていきましょう。
1270個のうち、10個余ったので1260個が面積となります。
補助線を引いて考えると、緑の部分の面積を大きい面積から1260個を引いて315個と求めることができます。
後は面積図に沿って計算すると9箱と求めることができます!


答えを見るにはここをクリック!
解答:20cm
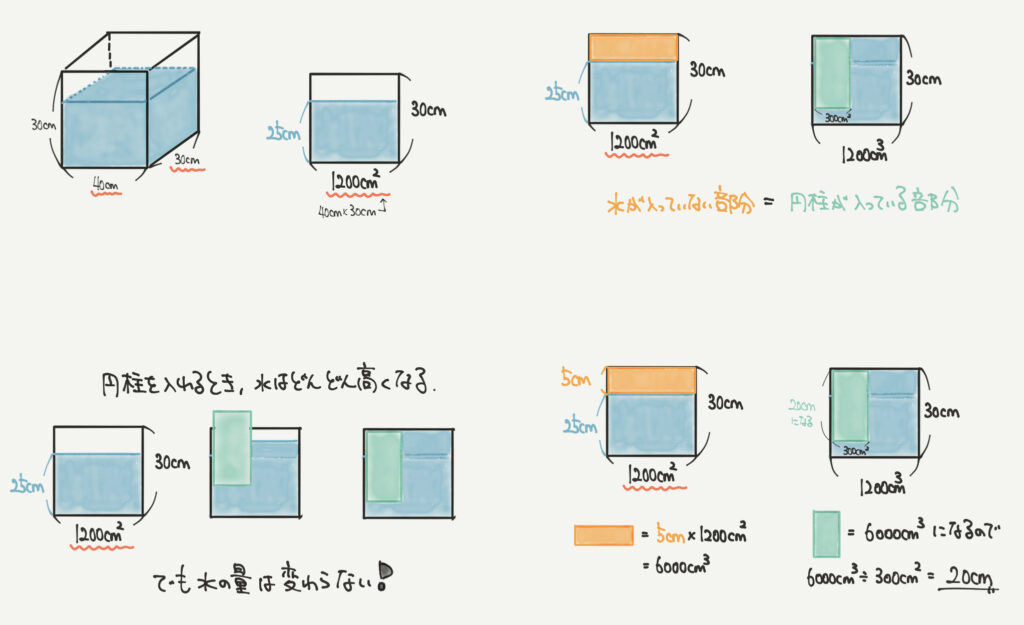

立体図形の面積図は他と違って底辺の単位がcmではなく、㎠となるのが特徴でした。
しかし根本の考えはたて×横です。
そこが変わらないのが面積図で解くポイントです。
この考えさえブレなければ必ず解けます!!大丈夫です。
深さ25cmなので5cm分の空白があります。
単位に注意して計算すると、6000㎤となり、
円柱の底面積300㎠から20cmまで入れることができることがわかります。
立体図形なんて難しすぎ!もっとわかりやすくしてくれという方は
こちらから「立体図形」の問題に挑戦していきましょう!!

まとめ
以上で面積図は終わりです!!おつかれさまでした。
面積図の基礎から問題演習まで、文字通り網羅できましたでしょうか?
面積図の意味はわかったけど、最後まで解けなかったという方は心配しないでください。
少なくとも面積図を理解しているのなら演習を重ねて、
その他の解法を学んで行けば必ず成績アップにつながります!
逆にこれを読んでも面積図ピンとこないよという方、本当に申し訳ありません。
もっとわかりやすい解説を心がけていこうと思います。
面積図攻略は中学受験算数の要です!一緒に頑張っていきましょう!!



